| Autor |
Nachricht |
Kracker
Anmeldungsdatum: 04.11.2016
Beiträge: 6
|
 Kracker Verfasst am: 04. Nov 2016 18:49 Titel: Mittlere thermische Geschwindigkeit |
 |
|
Meine Frage:
Hallo,
wir mussten die mittlere Thermische Geschwindigkeit von einem Gas herleiten.
Meine Ideen:
Dazu habe ich angenommen:
wobei f die Freiheitsgrade sind, kb Boltzmannfaktor und T die Temperatur.
Ich nehme an f=3 (oder 6 wegen der Impulse?)
wenn ich das nun auf v umstelle bekomme ich:
das ist aber nun die wahrscheinlichste Geschwindigkeit? In der Übung wurde mit der Formel:
gerechnet. Jetz frage ich mich woher dieses 8/pi kommt.
Danke schon mal für Antworten  |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 04. Nov 2016 19:15 Titel: |
|
|
Das eine ist die mittlere quadratische Geschwindigkeit (bzw. die Wurzel davon), das andere (mit 8 durch Pi) der mittlere Geschwindigkeitsbetrag, der sich aus
\,\mathrm{d}v)
ergibt (wobei f(v) die Maxwell-Boltzmannsche Geschwindigkeitsverteilung ist). |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 04. Nov 2016 20:51 Titel: |
|
|
Willkommen im Forum Kracker!
in die übliche Form v(T).
Die wahrscheinlichste Geschwindigkeit kann ich nicht nachvollziehen; bei mir 
PS Die mittlere thermische Geschwindigkeit wird auch als mittlere energetische Geschwindigkeit bezeichnet. |
|
|
Kracker
Anmeldungsdatum: 04.11.2016
Beiträge: 6
|
| Kracker Verfasst am: 08. Nov 2016 22:37 Titel: |
|
|
Also über:
^{3/2} \int_0^\infty \! v^{3}*e^{-\frac{m*v^{2}}{2*kb*t}} \, \dd v
<br />
)
verschwindet das Integral (also wird 1 bzw. -1 wenn ich mich nicht verrechnet habe) und übrig bleibt eben:
^{3/2}
<br />
)
aber wie komme ich da auf:
 |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 09. Nov 2016 18:50 Titel: |
|
|
|
Vielleicht guckst mal hier. Es gibt drei verschiedene Mittelwerte, Deine ist die mittlere. |
|
|
Kracker
Anmeldungsdatum: 04.11.2016
Beiträge: 6
|
| Kracker Verfasst am: 10. Nov 2016 10:52 Titel: |
|
|
| franz hat Folgendes geschrieben: | | Vielleicht guckst mal hier. Es gibt drei verschiedene Mittelwerte, Deine ist die mittlere. |
du meinst die quadratisch gemittelte Geschwindigkeit? Das mache ich doch nicht oder?
Über das integral bekommt man doch auf die mittlere (thermische) Geschwindigkeit? Ist der Koeffizient anders? Die Wikipedia Seite verwirrt mich etwas. Wichtig ist ja nur was in p(v) vor dem v^2 e^() steht. Was muss da für die mittlere thermische Geschwindigkeit stehen? |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 10. Nov 2016 21:48 Titel: Re: Mittlere thermische Geschwindigkeit |
|
|
Die hast oben nach der mittleren thermodynamischen = energetischen Geschwindigkeit 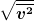 eines Idealen Gases gefragt. Wenn es noch darum geht: Die kann man anhand der Maxwell-Boltzmann-Verteilung p(v) berechnen und mit  gelangt man zu  .
Wo ist Dein Problem? |
|
|
Kracker
Anmeldungsdatum: 04.11.2016
Beiträge: 6
|
| Kracker Verfasst am: 11. Nov 2016 12:41 Titel: |
|
|
Naja erstens wie komme ich von ^{3/2} ) auf  ?
und wie komme ich dann von dem auf:
?
Alleine durch umformen komme ich da nicht drauf, und das ist doch die richtige Ausgangsformel oder? Wie die Boltzmannkonstante definiert ist weiß ich eh, aber alleine dieses hoch 3/2 passt nicht rein hier. Oder ist hier in der Annahme schon ein Fehler? |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 11. Nov 2016 23:34 Titel: |
|
|
Das Integral
\dd v )
ist nicht gleich 1, sondern
\dd v =2\left(\frac{k_B T }{m}\right)^2)
Zusammen mit dem Vorfaktor ergibt sich
 . |
|
|
Kracker
Anmeldungsdatum: 04.11.2016
Beiträge: 6
|
| Kracker Verfasst am: 12. Nov 2016 16:57 Titel: |
|
|
| Myon hat Folgendes geschrieben: | Das Integral
ist nicht gleich 1, sondern
Zusammen mit dem Vorfaktor ergibt sich
. |
ahh ok ich hab beim Integral einen fehler gemacht. Habs jetzt richtig rausbekommen.
danke!! |
|
|
Fry2000
Gast
|
| Fry2000 Verfasst am: 23. Mai 2023 12:24 Titel: |
|
|
Hallo; wie würde man so ein Integral denn lösen. Habe es mit der Produktregel für Integrale nicht geschafft. Un ich finde auch nichts passendes in der Intergraltafel.
Über hilfe oder Hinweise würde ich mich freuen
Gruß fry |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 23. Mai 2023 12:59 Titel: |
|
|
Du meinst wahrscheinlich
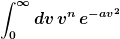
Zunächst substituiert man
Das führt auf Integrale der Form
Derartige Integrale berechnet man gerne mittels des Tricks
^k \int_0^\infty dU \, e^{-aU} )
wobei letzteres elementar lösbar ist.
Nun ist eventuell n sowie im hier vorliegenden Fall mit n=3 das k nicht ganzzahlig, d.h. man muss sich noch überlegen, inwiefern das Ergebnis auch für nicht ganzzahlige n bzw. k anwendbar ist.
Dabei verwendet man im Ergebnis die Gamma-Funktion (die die eindeutige Verallgemeinerung der Fakultät für nicht ganzzahlige Werte darstellt)
 = z \, \Gamma(z) \qquad z \in \mathbb{C} \setminus -1 )
 = (n-1)! \qquad n \in \mathbb{N}^+ )
Diese kann wiederum mittels des Integrals
 = \int_0^\infty dt \, t^{z-1} \, e^{-t}; \qquad \text{Re} z > 0)
definiert werden. Man könnte also das obige dU-Integral durch eine weitere Substitution direkt auf diese Form bringen:
 \, \left(a^{-1} t\right)^k \, e^{-t} = a^{-k-1} \, \Gamma(k+1))
(das ist nur eine kurze Skizze; bitte nochmal auf Details prüfen)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 23. Mai 2023 23:20, insgesamt einmal bearbeitet |
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
| Nils Hoppenstedt Verfasst am: 23. Mai 2023 13:29 Titel: |
|
|
Alternativ kann man das Integral auch mit der Produktregel lösen:
Nun setzt man
Ergo:
\right]_{0}^{\infty} + \frac{1}{2\alpha} \int_0^\infty \! 2x e^{-\alpha x^2} \, \dd x \\ &=& 0 +\frac{1}{\alpha} \left[-\frac{1}{2\alpha}e^{-\alpha x^2} \right]_{0}^{\infty} \\ &=&\frac{1}{2\alpha^2} )
Viele Grüße,
Nils
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
|
|
Registrieren
Login
FAQ
Suchen
