| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. März 2016 09:16 Titel: FAQ - Vakuumfluktuationen TomS Verfasst am: 25. März 2016 09:16 Titel: FAQ - Vakuumfluktuationen |
 |
|
Ich versuche an dieser Stelle anhand eines einfachen quantenmechanischen Modells zu erklären, welche Idee den sogenannten Vakuumfluktuationen zugrundeliegt. Die Erklärung kommt dabei ohne den Begriff der sogenannten "virtuellen Teilchen" aus.
Als Ausgangspunkt wähle ich ein Beispiel aus der QCD. Abschließend erkläre ich anhand des quantenmechanischen harmonischen Oszillators die wesentliche Idee.
Gegeben sei ein quantenmechanischer Zustand
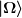
der sogenannte "Vakuumzustand" als Zustand niedrigster Energie
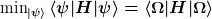
sowie mathematische Operatoren
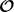
die den "Inhalt von Zuständen" nach bestimmten Kriterien berechnen.
Im Falle des Vakuumzustandes wären das die Erwartungswerte
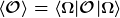
Der eigtl. interessante Punkt ist, dass das Vakuum nicht bzgl. aller physikalisch interessanter Operatoren "leer" ist, d.h. es existieren Operatoren, deren Erwartungswerte im Vakuum nicht Null sind. Diesen Umstand bezeichnet man mit dem Begriff Vakuumfluktuationen, den man von dem der "virtuellen Teilchen" unterscheiden muss.
Ein Beispiel wäre das Vakuum der QCD, d.h. der Zustand niedrigster Energie und zugleich der Zustand ohne jegliche "physikalische Quarks", Protonen, Neutronen, Pionen, ... Speziell betrachtet man einen "Anzahloperator" N für "physikalische Quarks". Für den Erwartungswert gilt
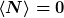
Verwendet man jedoch ein allgemeineres Objekt, so gilt interessanterweise
^3\,\text{GeV}^3)
Das sieht nun so aus, als ob im Vakuum in gewisser Weise tatsächlich Quarks existieren würden. Man bezeichnet dies als "Quarkkondensat". Der Wert ist physikalisch relevant, obwohl er nicht direkt, jedoch über Umwege, gemessen werden kann. Man kann nämlich zeigen, dass dieses Kondensat mit der Pionmasse sowie der Pion-Zerfallskonstanten zusammenhängt. Dabei zeigt sich außerdem, dass nicht-perturbative Beiträge existieren, die also nicht mittels des Formalismus der "virtuellen Teilchen" berechnet werden können.
Tatsächlich ist das Vakuum bzgl. dessen, was wir als "physikalisches Quark" bezeichnen, leer, jedoch nicht bzgl. anderer Operatoren, die von den Quarkfeldern abhängen.
Man muss zwischen dem Feld q(x) und einer teilchenartigen Anregung unterscheiden. Ein analoger Beispiel ist das Higgsfeld. Während im Vakuum sicher wieder
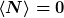
für den Anzahloperator der Higgsteilchen gilt, findet man für den Erwartungswert des Higgsfeldes
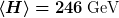
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 26. März 2016 08:56, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. März 2016 09:55 Titel: TomS Verfasst am: 25. März 2016 09:55 Titel: |
 |
|
Als einfachstes Beispiel dient der quantenmechanische harmonische Oszillator.
Die klassischen Lösungen sind harmonische Schwingungen
 = A\,\sin(\omega t + \phi_0))
 = A\omega\,\cos(\omega t + \phi_0))
Die Lösung niedrigster Energie entspräche einem im Nullpunkt ruhenden Teilchen, also
 = 0)
 = 0)
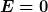
Wir betrachten in der QM nun ausschließlich den Grundzustand |0>, d.h. den Zustand niedrigster Energie.
Er hat die Eigenschaft, dass in ihm keine Schwingungsmoden existieren; mathematisch bedeutet dies, dass der Erwartungswert des Anzahloperators, der diese Moden zählt, verschwindet
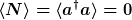
Ebenso findet man verschwindenden Orts- und Impulserwartungswert
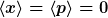
Das ist aus Symmetriegründen unmittelbar klar.
Berechnet man jedoch Orts- und Impulsunschärfe, also die Streuung des Ortes und des Impulses um diese Erwartungswerte, so findet man
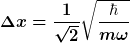
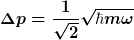
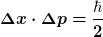
Im Grundzustand liegen also keine scharfer Werte für Ort bzw. Impuls vor.
Berechnet man den Erwartungswert des Quadrates des Impulses, so erhält man
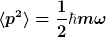
Das bedeutet, dass der Erwartungswert des Impulses Null ist, jedoch nicht der Erwartungswert des Quadrates des Impulses.
Für die Grundzustandsenergie findet man
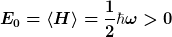
D.h. obwohl keine Schwingungsmoden existieren (der Erwartungswert für den Anzahloperator verschwindet, s.o.) verschwindet die Grundzustandsenergie nicht. Umgekehrt bedeutet dies, dass die nicht-verschwindende Grundzustandsenergie nicht von Schwingungsmoden getragen wird.
Im Falle des quantenmechanischen harmonischen Oszillators kann das Vakuum auf zweierlei Weisen definiert werden, die jedoch äquivalent sind. Zum einen definiert man das Vakuum gerade als Zustand mit verschwindender Modenanzahl, zum anderen definiert man man das Vakuum als Eigenzustand zu H mit minimaler Energie.
Diese beiden Definitionen sind in der Quantenfeldtheorie üblicherweise nicht mehr äquivalent. Das physikalische Vakuum muss als Zustand minimaler Energie definiert werden und entspricht dann nicht zwingend dem perturbativen Vakuum verschwindender Modenanzahl (bzw. erst, wenn die Moden geeignet undefiniert werden). Beispiele dafür sind Supraleiter, Higgs-Vakuumerwartungswert und Quark-Kondensat (allesamt Beispiele für spontan gebrochene Symmetrien).
Die Berechnungen zum Vakuumzustand in Quantenfeldtheorien sind wesentlich komplizierter, gehen aber im Kern auf ähnliche Überlegungen wie in der QM zurück.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 25. März 2016 10:39, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
|
 |
|
|















