| Autor |
Nachricht |
rüdisüli
Anmeldungsdatum: 23.09.2015
Beiträge: 95
|
 rüdisüli Verfasst am: 06. März 2016 15:07 Titel: Magnetismus relativistisch |
 |
|
Magnetismus ist angeblich ein relativistisches Phänomen, z.B. gemäss diesem Dokument:
http://www.ate.uni-due.de/data/postgraduate_lecture/Relativit%C3%A4t_elektr_und_mag_Felder.pdf
Hier wird ein Strom in einem Leiter und ein bewegtes Probeelektron betrachtet. Die betreffende Lorentzkraft wird von der relativen Geschwindigkeit des Probeelektrons im Verhältnis zum positiv geladenen Leiter (ohne Elektronen) abgeleitet, wobei der Strom und das Probeelektron dieselbe Geschwindigkeit v haben. Dabei spielt die Längenkontraktion der Kationen des Leiters eine Rolle, und die Kraft wird elektrostatisch begründet.
Wie funktioniert diese Betrachtung nun wenn das Probeelektron nicht dieselbe Geschwindigkeit hat wie der Strom? Der Strom wäre derselbe wie beim obigen Fall und mit demselben H-Feld verbunden. Das Probelektron hätte aber z.B. nur die Geschwindigkeit ½*v. Gemäss der herkömmlichen Betrachtung mit der Formel FL= µ0*H*Q*v wäre die Lorentzkraft halb so gross wie beim obigen Fall. Wie könnte dies nun relativistisch betrachtet werden? Im Verhältnis zum Probeelektron als ruhendes Bezugssystem haben sowohl die Elektronen des Leiters als auch die Kationen des Leiters eine relative Geschwindigkeit mit dem Betrag ½*v. Wären dann nicht auch beide Teile des Leiters mit derselben Längenkontraktion verbunden, wobei dann keine Kraftwirkung davon abgeleitet werden könnte? |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 06. März 2016 17:52 Titel: Re: Magnetismus relativistisch |
|
|
Hallo,
| rüdisüli hat Folgendes geschrieben: | Wie funktioniert diese Betrachtung nun wenn das Probeelektron nicht dieselbe Geschwindigkeit hat wie der Strom?
|
Ich beziehe mich auf Bild 1:
Wenn Du Dich in einem Bezugssystem befindest, in dem das außen befindliche Elektron ruht, so ist der magn. Teil der Lorentzkraft, die auf dieses Elektron wirkt, definitionsgemäß gleich null. Schließlich hat das Elektron, auf das die Kraft wirken soll, die Geschwindigkeit  , so dass gilt:
 = q \vec E)
In diesem Bezugssystem reden wir also immer nur von Coulombkräften.
Um Coulombkraft auf das außen befindliche Elektron zu berechnen, würdest Du nun die Linienladungsdichte des Leiters berechnen. Dazu sind dann alle Ladungen (Atomrümpfe + Elektronen) in die Rechnung mit einzubeziehen.
Je schneller sich diese Ladungen aus Sicht des von Dir gewählten Bezugssystems bewegen, umso stärker schlägt die Längenkontraktion zu. Das bedeutet, dass die Abstände der Ladungen im Vergleich mit einem System, in dem die Ladungen ruhen, kleiner sind. Die Linienladungsdichte der schnellen Ladungen ist somit größer.
Wenn der Leiter zum Beginn des Experiments (vor dem Einschalten des Stromes) ungeladen war und sich das äußere Elektron mit der Hälfte der Driftgeschwindigkeit der Elektronen bewegt, ist die Kraft auf das äußere Elektron gleich null.
Viele Grüße
Michael
* Solange die Geschwindigkeiten aber alle deutlich kleiner als c bleiben, ist 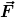 in allen Systemen näherungsweise gleich groß. |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 06. März 2016 18:17 Titel: Re: Magnetismus relativistisch |
|
|
Ich möchte den Admins vorschlagen, diesen Thread in Elektrik zu verschieben (notfalls auch in Mechanik, weil dort relativistische Effekte untergebracht werden sollen).
[jh8979: Erledigt.] |
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 06. März 2016 20:54 Titel: |
|
|
Falls es Dich interessiert: E- und B-Feld unterliegen beim Inertialsystemwechsel einer Lorentz-Transformation (allerdings nicht der Lorentz-Transformation eines Vierervektors ) , sondern der eines Tensors zweiter Stufe: des sog. Feldstärketensors). Wenn man es nicht kovariant schreibt, erkennt man vielleicht nicht unmittelbar den Zusammenhang zur "üblichen" Lorentz-Transformation. Das Ergebnis (dessen Herleitung etwas aufwendiger ist) findest Du hier:
https://de.wikipedia.org/wiki/Lorentz-Transformation#Lorentz-Transformation_f.C3.BCr_das_elektromagnetische_Feld |
|
|
rüdisüli
Anmeldungsdatum: 23.09.2015
Beiträge: 95
|
| rüdisüli Verfasst am: 07. März 2016 08:52 Titel: |
|
|
@Michael: Danke für die Ausführungen. Dass die resultierende Kraft bei der 2. der oben beschriebenen Situationen 0 sein würde, wenn man dies relativ betrachtet, habe ich geahnt. Mein Problem ist der Widerspruch zur herkömmlichen Formel FL=q*v*B. Gemäss dieser sollte die Lorentzkraft hier eben nicht 0 sein.
Ich weiss nicht, wie dieser Widerspruch überwunden werden kann. Ist die herkömmlichen Formel falsch oder nicht allgemein gültig? Was wäre denn die korrekte Formel für bewegte Ladungen im Magnetfeld? |
|
|
rüdisüli
Anmeldungsdatum: 23.09.2015
Beiträge: 95
|
| rüdisüli Verfasst am: 07. März 2016 19:40 Titel: |
|
|
|
Gemäss "FL=q*v*B" sollte es im Prinzip egal sein, aus welchem System sich das B-Feld ergibt. Ein weiterer problematischer Fall: Wenn der Strom (in einem Leiter) senkrecht zum Geschwindigkeitsvektor der mit v bewegten Punkladung verläuft, wie kann man dann die Lorentzkraft relativistisch erklären? Ist hier die relativistische Betrachtung überhaupt angebracht und sinnvoll? |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 07. März 2016 21:58 Titel: |
|
|
Hallo,
| rüdisüli hat Folgendes geschrieben: | | @Michael: Danke für die Ausführungen. Dass die resultierende Kraft bei der 2. der oben beschriebenen Situationen 0 sein würde, wenn man dies relativ betrachtet, habe ich geahnt. |
Ich bin unbedingt dafür, jedes elektrodynamische Problem relativistisch zu betrachten. Es geht nämlich schlicht nicht anders, wenn man die Maxwellgleichungen nutzen will.
| Zitat: | | Mein Problem ist der Widerspruch zur herkömmlichen Formel FL=q*v*B. |
Ich habe mir das mit folgendem Gedankenexperiment erklärt:
Wir betrachten einen
- im Laborsystem ruhenden Stromkreis und nehmen für die folgenden Betrachtungen an,
- dass dieser von der Erde elektrisch isoliert ist (z. B. Batteriestromkreis) und
- im stromlosen Zustand einen ausgeglichene Ladungsbilanz aufweist.
Neben diesen Stromkreis plazieren wir ein einzelnes Elektron, das ebenfalls im Laborsystem ruhen soll.
Sobald wir den Strom einschalten, müsste das Elektron vom Leiter elektrostatisch abgestoßen werden, da der Leiter nun aus Sicht des Laborsystems eine von null verschiedene (negative) Ladungsdichte aufweist*.
Üblicherweise vernachlässigt man diesen Kraftanteil, wenn man Kräfte auf Ladungen außerhalb eines Leiters betrachtet und berechnet nur den magn. Anteil der Kraft. Sicherlich wird das in den allermeisten technischen Anwendungen auch berechtigt sein, zumal man den Leiter ja auch sehr oft irgendwo geerdet hat.
Viele Grüße
Michael |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 08. März 2016 00:33 Titel: |
|
|
Hallo,
| rüdisüli hat Folgendes geschrieben: | | Ein weiterer problematischer Fall: Wenn der Strom (in einem Leiter) senkrecht zum Geschwindigkeitsvektor der mit v bewegten Punkladung verläuft, wie kann man dann die Lorentzkraft relativistisch erklären? Ist hier die relativistische Betrachtung überhaupt angebracht und sinnvoll? |
Elektrodynamik auf Basis der Maxwellgleichungen kann ausschließlich relativistisch betrachtet werden.
| Zitat: |
Wenn der Strom (in einem Leiter) senkrecht zum Geschwindigkeitsvektor der mit v bewegten Punkladung verläuft, wie kann man dann die Lorentzkraft relativistisch erklären? |
Ok, das habe ich soweit noch nicht durchdacht.
Du hast also eine Punktladung, die sich (aus dem Laborsystem betrachtet) senkrecht auf einen stromführenden Leiter zubewegt.
Skizze:
stromführender Leiter, Pfeil = Elektronenrichtung
-->---------------------------------------------------
.
.
.
.
......................^
......................|
......................o pos. Punktladung mit Flugrichtung (nach rechts abgel.)
Wir wechseln nun das Bezugssystem. Stell Dir also vor, Du sitzt gewissermaßen auf der positiv gel. Punktladung drauf und fliegst mit. Aus diesem Bezugssystem betrachtet ist die Geschwindigkeit der Punktladung gleich null.
Was würdest Du sehen:
- Bei den Atomrümpfen ist die Situation links und rechts symmetrisch. Das bedeutet wohl, dass die Atomrümpfe die Punktladung weder nach links noch nach rechts ablenken wollen.
- Bei den Elektronen ist die Sache leicht unsymmetrisch, da die Elektronen ja zusätzlich eine Komponente nach rechts haben. Für die von links kommenden Elektronen bedeutet nach rechts "auf Dich zu". Für die recht fliegenden Elektronen bedeutet nach rechts "von Dir weg". Ich denke, das wäre ein Ansatzpunkt, ohne dass ich aber jetzt überblicke, ob das letztlich so aufgeht.
Günstiger ist es wahrscheinlich aber schon, das Problem zunächst in einem Bezugssystem zu berechnen, in dem sich sowas einfach berechnen lässt und anschließend die Größen mithilfe der Lorentztransformation
https://de.wikipedia.org/wiki/Lorentz-Transformation
zu transformieren.
Viele Grüße
Michael |
|
|
rüdisüli
Anmeldungsdatum: 23.09.2015
Beiträge: 95
|
| rüdisüli Verfasst am: 08. März 2016 13:50 Titel: |
|
|
Vielen Dank für die ausführlichen Antworten. Ganz gelöst erscheint mir dies allerdings noch nicht.
"Sobald wir den Strom einschalten, müsste das Elektron vom Leiter elektrostatisch abgestoßen werden, da der Leiter nun aus Sicht des Laborsystems eine von null verschiedene (negative) Ladungsdichte aufweist."
Dadurch verschiebt sich nun der Widerspruch gegenüber "FL=q*v*B" auf einen weiteren Fall, mit einem gegenüber dem Leitersystem ruhenden Probeelektron. Gemäss "FL=q*v*B" sollte die Lorentzkraft hier allerdings Null sein.
> Ich weiss nach wie vor nicht, was ich von dieser Formel halten soll, und inwiefern bzw. unter welchen Voraussetzungen sie vielleicht als "näherungsweise richtig" betrachtet werden könnte.
Existiert irgendwo eine Beschreibung, welche dies beantworten würde?
Oder sollte ich alternativ dazu vielleicht die SRT hinterfragen?
Ein weiteres Problem der relativistischen Betrachtungseise sehe ich ferner im Zusammenhang mit geschossenen Leiterschleifen: Bei schnellen Strömen in Ringleiter-Systemen wäre die Folge der Längenkontraktion, dass der Leiter aus der Sicht eines ruhenden Beobachters in zwei Teile zerfallen müsste. D.h., es würden 2 konzentrische Kreise entstehen, wobei der innere aus den bewegten Elektronen bestünde. Dessen Radius könnte theoretisch bis auf null schrumpfen.
Da diese (bisherigen) Betrachtungen theoretischer Natur sind, würde es mich nun interessieren, inwiefern zu diesem Thema auch experimentelle Nachweise existieren.
> Wurde z.B. der oben zitierte Fall (gegenüber dem Leitersystem ruhende Probe-Punktladung) jemals experimentell überprüft?
> Was ist überhaupt die experimentelle Basis für "bewegte Ladungen im Magnetfeld" bzw. für "FL=q*v*B"?
Geht es hier hauptsächlich um geladene Teilchen mit relativ grossen Geschwindigkeiten (z.B. 50%*c) im Zusammenhang mit Teilchenbeschleunigern?
Oder gibt es vielleicht auch Experimente mit relativ grossen und langsamen Kugelladungen, die im Physiklabor einer Schule eins zu eins beobachtet werden könnten?
Auf weitere Reaktionen/ Antworten würde ich mich freuen.
LG |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 08. März 2016 21:19 Titel: |
|
|
Hallo,
| rüdisüli hat Folgendes geschrieben: | Vielen Dank für die ausführlichen Antworten. Ganz gelöst erscheint mir dies allerdings noch nicht.
"Sobald wir den Strom einschalten, müsste das Elektron vom Leiter elektrostatisch abgestoßen werden, da der Leiter nun aus Sicht des Laborsystems eine von null verschiedene (negative) Ladungsdichte aufweist."
Dadurch verschiebt sich nun der Widerspruch gegenüber "FL=q*v*B" auf einen weiteren Fall, mit einem gegenüber dem Leitersystem ruhenden Probeelektron. Gemäss "FL=q*v*B" sollte die Lorentzkraft hier allerdings Null sein.
> Ich weiss nach wie vor nicht, was ich von dieser Formel halten soll, und inwiefern bzw. unter welchen Voraussetzungen sie vielleicht als "näherungsweise richtig" betrachtet werden könnte.
|
Die Gleichung
)
gibt in allen Inertialsystemen die elektromagnetische Gesamtkraft auf eine Ladung, die in diesem Bezugssystem mit der Geschwindigkeit 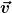 bewegt, richtig wieder.
Hierzu mehrere Hinweise:
1) Diese Kraft weist nicht notwendigerweise in allen Bezugssysteme den gleichen Zahlenwert auf. Eine elegantere Möglichkeit für die Behandlung von Kräften im Rahmen der speziellen Relativitätstheorie sind Vierervektoren (https://de.wikipedia.org/wiki/Vierervektor#Viererkraft_und_Bewegungsgleichung).
2) ABER: Die Kraft 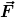weist in zwei Inertialsystemen, die sich gegeneinander mit einer Geschwindigkeit 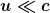 bewegen, näherungsweise den gleichen Zahlenwert auf. Diese Gleichung ist daher für die allermeisten praktischen (auf Newtonmechanik beruhenden) Anwendungen ganz ausgezeichnet nutzbar.
3) GEWÖHNUNGSBEDÜRFTIG: ist am Anfang, dass die Zusammensetzung (elektrischer und magnetischer Anteil) sehr stark mit dem Bezugssystem ändert, und zwar auch schon, wenn sich beide Inertialsysteme nur langsam gegeneinander bewegen.
Beispiel zu 3):
Ein Zug bewegt sich im Erdmagnetfeld. An einem Sitzplatz liegt auf dem Tisch (waagerecht) eine Metallstange.
- Ein Beobachter, der am Bahnsteig sitzt, wird sagen, dass dieser Metallstab elektrisch aufgeladen ist, da auf die Leitungselektronen eine Lorentzkraft wirkt, die die Ladungen so lange verschiebt, bis die Lorentzkraft und die Coulombkraft gerade im Gleichgewicht sind.
 = 0)
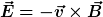
Mit einem auf dem Bahnhof ruhenden Voltmeter wird er die zugehörige Spannung ggf. auch messen können (z. B. als Spannung zwischen den Schienen, wenn man den Zug selbst als die "Metallstange" ansieht).
- Ein Beobachter, der im Zug sitzt (alle Größen mit Strich' für dieses Bezugssystem), wird ebenfalls sagen, dass keine Kraft auf die Elektronen wirkt. Er wird für den Metallstab jedoch die Geschwindigkeit 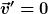 angeben und kommt in seiner Rechnung auf:
 = 0)
Mit einem mitgeführten Voltmeter wird er tatsächlich die Spannung 0 messen!
Du kennst das zugehörige Experiment vielleicht in der Form:
https://de.wikipedia.org/wiki/Elektromagnetische_Induktion#Bewegter_Leiterstab_im_Magnetfeld
| Zitat: |
Existiert irgendwo eine Beschreibung, welche dies beantworten würde?
Oder sollte ich alternativ dazu vielleicht die SRT hinterfragen? |
Die Maxwellgleichungen sind durch und durch relativistisch (spez. Rel.-Th.). Über sie kam Einstein ja erst auf die spez. Relativitätstheorie. In diesem Artikel findest Du erste weitere Hinweise:
https://de.wikipedia.org/wiki/Spezielle_Relativit%C3%A4tstheorie#Lorentzkontraktion
Später wirst Du dann aber sicherlich direkt die Lorentztransformation anwenden wollen, ohne jedesmal Elektronen zu zählen und deren Abstände zu berechnen.
https://de.wikipedia.org/wiki/Lorentz-Transformation
| Zitat: |
Ein weiteres Problem der relativistischen Betrachtungseise sehe ich ferner im Zusammenhang mit geschossenen Leiterschleifen: Bei schnellen Strömen in Ringleiter-Systemen wäre die Folge der Längenkontraktion, dass der Leiter aus der Sicht eines ruhenden Beobachters in zwei Teile zerfallen müsste. D.h., es würden 2 konzentrische Kreise entstehen, wobei der innere aus den bewegten Elektronen bestünde. Dessen Radius könnte theoretisch bis auf null schrumpfen.
|
Es gibt eine Menge Paradoxa (scheinbare Widersprüche) zur speziellen Relativitätstheorie. In dem Wikipediaartikel zur Lorentzkontraktion geht es z. B. um einen Zug, der je nach Bezugssystem länger oder kürzer ist.
Im "Bahnhofssystem" gemessen passt der Zug auf den Bahnsteig, im "Mitfahrersystem" meint man intuitiv, er würde nicht reinpassen. Man kann bei solchen Paradoxa immer eine ganze Weile verbringen, bis man den Knackpunkt gefunden hat.
Ich denke, die Auflösung bei der Frage "Passt der Elektronenstromkreis in den Leiter hinein" ist ganz ähnlich wie bei der Bahnhofsgeschichte.
M.E. sollte man dabei auch ein wenig seine Anschauung hinterfragen.
Wir als Menschen stellen intuitive Regeln zur Frage "Unter welchen Bedingungen passt ein Objekt ins andere rein?" auf Grundlage der Newtonmechanik auf. Ganz konkret: Wir lernen das als kleine Kinder, wenn wir mit Bauklötzen spielen. Ein eckiger Klotz passt in ein gleich großes eckiges Loch. Ein großer, grüner, eckiger Klotz passt trotzdem nicht in ein kleines, rundes Loch, obwohl dieses Loch auch grün ist. usw.
Diese Regeln müssen bei relativistischen Anwendungen nicht unbedingt gelten.
| Zitat: |
> Wurde z.B. der oben zitierte Fall (gegenüber dem Leitersystem ruhende Probe-Punktladung) jemals experimentell überprüft?
|
Mir ist das nicht bekannt. Das wäre auch sicherlich sehr aufwendig, da die vorhergesagten E-Felder sehr klein sind und erst einmal von den statischen E-Feldern unterschieden werden müssten, die zum Aufrechterhalten des Stromkreises benötigt werden.
| Zitat: |
Oder gibt es vielleicht auch Experimente mit relativ grossen und langsamen Kugelladungen, die im Physiklabor einer Schule eins zu eins beobachtet werden könnten?
|
Langsam: https://de.wikipedia.org/wiki/Fadenstrahlrohr
Schnell: https://de.wikipedia.org/wiki/Kathodenstrahlr%C3%B6hre (für mittelalte bis alte Semester auch unter dem Begriff "Fernseher" bekannt)
Viele Grüße
Michael
Zuletzt bearbeitet von ML am 09. März 2016 13:32, insgesamt 2-mal bearbeitet |
|
|
rüdisüli
Anmeldungsdatum: 23.09.2015
Beiträge: 95
|
| rüdisüli Verfasst am: 09. März 2016 12:33 Titel: |
|
|
Danke. Um dies verarbeiten zu können, muss ich zuerst nachfragen:
> Zu 2): Was konkret wären hier (im vorliegenden Fall) die 2 erwähnten Inertialsysteme?
Betrifft dies vielleicht die Punktladung und das Leitersystem (bzw. einen Teil davon)?
> Was bedeutet hier "u" (auch im Unterscheid zu "v")?
Relativgeschwindigkeit zwischen was und was?
Gruss |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 09. März 2016 13:27 Titel: |
|
|
Hallo,
| rüdisüli hat Folgendes geschrieben: | Danke. Um dies verarbeiten zu können, muss ich zuerst nachfragen:
> Zu 2): Was konkret wären hier (im vorliegenden Fall) die 2 erwähnten Inertialsysteme? |
Zunächst einmal zwei beliebige Inertialsysteme. In diesen sitzt jeweils (tatsächlich oder nur gedanklich) ein Beobachter und beschreibt die Feldgrößen. Beide bekommen in aller Regel beim gleichen Experiment unterschiedliche Werte für die Feldgrößen heraus, je nachdem, in welchem Inertialsystem gemessen wird. Die Größen können aber mithilfe der Lorentztransformation ineinander umgerechnet werden.
Im Beispiel mit dem Zug bieten sich als (näherungsweise*) Inertialsysteme an:
- Das System, in dem der Bahnhof ruht.
- Das System, in dem der Zug ruht.
Als Inertialsystem ist aber auch ein System möglich, in dem ein (z. B. entgegenkommender oder halb so schneller) Zug ruht oder ein System, in dem ein gerade am Bahnhof spazierengehender Beobachter ruht.
| Zitat: |
> Was bedeutet hier "u" (auch im Unterscheid zu "v")?
Relativgeschwindigkeit zwischen was und was?
|
u soll hier die Geschwindigkeit sein, die ein Beobachter, der in einem beliebigen Inertialsystem n sitzt für ein anderes Inertialsystem m misst.
v ist in dem Beispiel die Geschwindigkeit einer Ladung in einem Inertialsystem 1.
v' ist in dem Beispiel die Geschwindigkeit der gleichen Ladung in einem Inertialsystem 2.
Viele Grüße
Michael
* näherungsweise, weil die Erde sich um sich selbst, um die Sonne u. ä. dreht sowie weil sie eine Masse hat |
|
|
|
|
Registrieren
Login
FAQ
Suchen
