| Autor |
Nachricht |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 21. Feb 2006 16:14 Titel: Bahn einer Sonde (horizontaler "Wurf" um Planeten) para Verfasst am: 21. Feb 2006 16:14 Titel: Bahn einer Sonde (horizontaler "Wurf" um Planeten) |
 |
|
Hallo,
folgendes Problem zu dem mir momentan noch etwas der Ansatz fehlt: eine Sonde umkreist einen Planeten der Masse M mit der Geschwindigkeit v auf einer Kreisbahn mit dem Radius r. In sehr kurzer Zeit wird ihre (tangentiale) Geschwindigkeit aber auf v-Δv abgebremst, so dass sie beginnt sich dem Planeten zu nähern. Wie groß ist der Abstand r' vom Planetenzentrum und die Geschwindigkeit v' der Sonde, wenn sie einmal halb um den Planeten "herumgefallen" ist?
Mein Ansatz ging jetzt in Richtung Erhaltungssätze - Energie und Drehimpuls:
^2 + 2 \cdot \gamma \cdot \frac{M}{r} = v'^2 + 2 \cdot \gamma \cdot \frac{M}{r'})
 = r' \cdot v')
Stimmt das erstmal so weit? Aber irgendwie fehlt ja noch was - die Angabe dass gerade um den halben Planeten gefallen wurde muss sich doch noch irgendwie verwerten lassen.
Na ja, ich bin schonmal auf die Ideen gespannt. 
para
_________________
Formeln mit LaTeX |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Feb 2006 16:53 Titel: dermarkus Verfasst am: 21. Feb 2006 16:53 Titel: |
 |
|
Das würde ich ganz ohne Rechnerei lösen.
v' = v - \Delta v
und r' = r.
Denn das Problem ist ja symmetrisch. Der Anfangspunkt und der Punkt "nach einmal halb herumfallen" sind die beiden Punkte der ellipsenförmigen Flugbahn, die am weitesten von dem umkreisten Planeten entfernt sind.
Einzige Einschränkung: Delta v darf nicht zu groß sein, sonst knallt der Körper auf den Planeten oder gerät in dessen Atmosphäre und wird abgebremst.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 21. Feb 2006 17:01 Titel: schnudl Verfasst am: 21. Feb 2006 17:01 Titel: |
 |
|
Wenn er Abbremsvorgang schlagartig erfolgt, so muss die neue Bahn eigentlich eine gültige "Planetenbahn" sein. Es kommt eigentlich nur eine Ellipse in Frage.
Die Sonde befindet sich dann zum Anfangszeitpunkt am Aphel der Ellipse, wenn Sie den Perihel erreicht, hat sie Die Erde halb umrundet. Im Brennpunkt dieses (näheren) Scheitels steht die Erde.
Die Exzentrizität ist mit der gesamt-Energie T+V verknüpft durch (hab ich aus Formelsammlung):

wobei a die grosse Halbachse der Kepler Elipse ist.
Aus dem bekannten E kann man a und damit auch den Perihel ausrechnen. Die Geschwindigkeit folgt dann aus Energieerhaltung. Ich nehme an sie ist grösser als die urprüngliche, da man sich ja näher beim Planeten befindet.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 21. Feb 2006 18:11, insgesamt 2-mal bearbeitet |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 21. Feb 2006 17:07 Titel: schnudl Verfasst am: 21. Feb 2006 17:07 Titel: |
 |
|
| Zitat: | | Denn das Problem ist ja symmetrisch. |
stimmt das denn ? Der Aphel kann ja viel viel weiter weg sein als der Perihel, da die Erde/Sonne ja in einem Brennpunkt steht und sich nicht im Mittelpunkt der Ellipse befindet...
Sicher bin ich mir nicht (hab auch nicht viel Zeit zum Nachdenken - habe gerade Projektrevision...), aber mir kommt es etwas komisch vor.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 21. Feb 2006 17:44 Titel: as_string Verfasst am: 21. Feb 2006 17:44 Titel: |
 |
|
Hallo!
Ich glaube auch eher, dass nach einer halben Umdrehung der Planeten-nächste Punkt auf der ellipstischen Bahn der Sonde erreicht ist.
Wie rechnet man das aber dann? Da muß ich auch mal überlegen...
Gruß
Marco
Edit: Nach kurzem Überlegen ist mir eingefallen: War da nicht mal was mit effektivem Potential? Man kann die Bewegung doch als eine eindimensionale in einem Effektiven Pot. betrachten. Beim Abbremsen befindet sich die Sonde ganz außen in dem Potential und nach einer halben Umdrehung ganz innen. Ich weiß aber jetzt gerade nicht mehr, wie das genau funktioniert hat...
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 21. Feb 2006 18:04 Titel: schnudl Verfasst am: 21. Feb 2006 18:04 Titel: |
 |
|
| Zitat: | | Ich glaube auch eher, dass nach einer halben Umdrehung der Planeten-nächste Punkt auf der ellipstischen Bahn der Sonde erreicht ist. |
Ja, ich denke schon ...
Die Energie T+V bestimmt denk ich alleine die grosse Halbachse a der Elipse (siehe oben). Da die Gesamtenergie am Anfang berechenbar ist (Geschwindigkeit gegeben, Abstand gegeben), sollte man auf a leicht schliessen können (zum Einsetzen bin ich zu faul). Wenn a gegeben ist, dann hat man das Perihel - die Sonne steht ja in einem Brennpunkt:

Insofern ist das schon symmetrisch, aber eben nicht zentralsymmetrisch, sonst hätte man ja eine Kreisbahn.
Die Gleichungen für Plantenbahnen und die Beziehungen der Energie (oben) zu den Bahnformen werden in jedem Standardwerk der Mechanik hergeleitet.
PS: Meine Gleichung gilt natürlich für eine Einheitsmasse !
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 21. Feb 2006 18:14, insgesamt einmal bearbeitet |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 21. Feb 2006 18:34 Titel: schnudl Verfasst am: 21. Feb 2006 18:34 Titel: |
 |
|
Für Kreisbahn gilt der Virialsatz (bekannt auch vom Bohrschen Modell des Wasserstoffs)


Nach der Reduktion hat man ganz am Anfang da W(pot) unverändert
 = m(v^2/2-v \Delta v + \Delta v^2/2) )
 = - \frac{1}{2} \cdot G \cdot \frac{M}{a} )
Daraus lässt sich a und damit auch der Perihel trivial ausrechnen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Feb 2006 19:26 Titel: Re: Bahn einer Sonde (horizontaler "Wurf" um Plane dermarkus Verfasst am: 21. Feb 2006 19:26 Titel: Re: Bahn einer Sonde (horizontaler "Wurf" um Plane |
 |
|
Hallo nochmal,
entschuldigt meinen Schnellschuss, das oben von mir war falsch.
Wie schnudl richtig sagt, gilt:
(1. Keplersches Gesetz:)
Die Bahn ist eine Ellipsenbahn mit dem Planeten in einem der beiden Brennpunkte der Ellipse.
Damit ist die Sonde nach einmal halb herumfallen auf ihrem planetennächsten Punkt angelangt und dort am schnellsten.
para, dein Ansatz ist sehr spannend. Denn deine Gleichung für den Drehimpulserhaltungssatz ist falsch, aber dein System zweier Gleichungen liefert meiner Meinung nach (neben der trivialen Lösung v'=v- \Delta v und r'=r für den Anfangspunkt der Bahn) genau die richtige Lösung.
Denn erstens müsste im richtigen Drehimpulserhaltungssatz (2. Keplersches Gesetz) statt der Bahngeschwindigkeit die Komponente der Bahngeschwindigkeit senkrecht zum Verbindungsvektor Planet-Sonde stehen.
Und zweitens sind genau die zwei Punkte der Bahn, um die es in dieser Aufgabe geht, diejenigen, bei denen die Bahngeschwindigkeit auf der Ellipse eben doch genau senkrecht zu diesem Verbindungsvektor steht.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 22. Feb 2006 00:31 Titel: Re: Bahn einer Sonde (horizontaler "Wurf" um Plane dermarkus Verfasst am: 22. Feb 2006 00:31 Titel: Re: Bahn einer Sonde (horizontaler "Wurf" um Plane |
 |
|
Damit das Gleichungssystem und das Resultat auch wirklich zum richtigen Ergebnis führen (wie eben beschrieben), muss zusätzlich im Energieerhaltungssatz ein Vorzeichenfehler korrigiert werden: So wie sie hier steht, benötigt die potentielle Energie in beiden Fällen ein negatives Vorzeichen (denn die potentielle Energie bei r ist ja größer als die bei r'):
^2 - 2 \cdot \gamma \cdot \frac{M}{r} = v'^2 - 2 \cdot \gamma \cdot \frac{M}{r'})
 = r' \cdot v')
Damit erhalte ich für v':
)
und für r':
)
mit den folgenden Bezeichnungen für die Größen direkt nach dem anfänglichen Abbremsen:
Radius

Geschwindigkeit
 , ,
kinetische Energie

und potentielle Energie im Gravitationsfeld

|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 22. Feb 2006 01:39 Titel: dermarkus Verfasst am: 22. Feb 2006 01:39 Titel: |
 |
|
Ergänzt man in schnudls Gleichungen die Faktoren 2 (wegen a = Halbachse) und m:


so kommt man mit seinem Weg zum selben Ergebnis.
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 22. Feb 2006 11:41 Titel: para Verfasst am: 22. Feb 2006 11:41 Titel: |
 |
|
Danke erstmal für die vielen hilfreichen Antworten. :)
| schnudl hat Folgendes geschrieben: | Die Exzentrizität ist mit der gesamt-Energie T+V verknüpft durch (hab ich aus Formelsammlung):

wobei a die grosse Halbachse der Kepler Elipse ist. |
Okay, eigentlich sollte man die Aufgabe ohne Formelsammlung lösen können aber die Gleichung ist trotzdem interessant. Was meinst du mit "T+V"? V steht für das Potential, oder? Und wie ist das mit der Einheitsmasse in dem Zusammenhang zu verstehen?
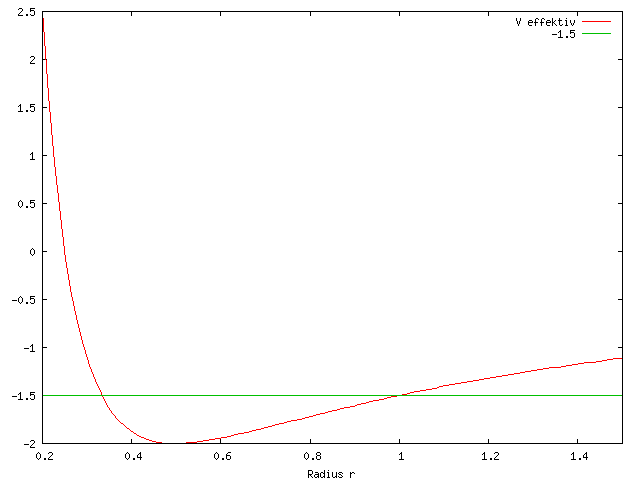
| as_string hat Folgendes geschrieben: | | Ich habe das mit dem Veff mal geplottet. Damit solltest Du die Aufgabe lösen können, denke ich :) |
Danke, ehrlicherweise weiß ich damit aber nicht zuviel anzufangen. Wofür steht das -1,5 und was sagt mir das V(r)?
| schnudl hat Folgendes geschrieben: | 
 |
Viralsatz sagt mir zwar nichts, aber zumindest die zweite Gleichung ist logisch. Wofür steht das E in der ersten Gleichung? Aber auch ein schöner Ansatz auf den man mal kommen muss. :)
| dermarkus hat Folgendes geschrieben: | | Damit das Gleichungssystem und das Resultat auch wirklich zum richtigen Ergebnis führen (wie eben beschrieben), muss zusätzlich im Energieerhaltungssatz ein Vorzeichenfehler korrigiert werden |
Danke, darin lag wohl das Problem dass ich keine sinnvolle Lösung rausbekommen habe. Dass der Drehimpuls eigentlich aus dem Kreuzprodukt herrührt hatte ich auch erst nicht beachtet, so dass die Gleichung für jeden Punkt der Bahn gleich ausgesehen hätte (was mir etwas suspekt gewesen wäre). Aber da das so ja nur für diese zwei Punkte gilt, ist jetzt wohl auch die Information mit dem halben Umlauf untergebracht. - Sehr schön. :)
_________________
Formeln mit LaTeX |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 22. Feb 2006 13:20 Titel: schnudl Verfasst am: 22. Feb 2006 13:20 Titel: |
 |
|
| Zitat: | | Wofür steht das E in der ersten Gleichung? |
Für die Gesamtenergie:

Der Virialsatz ... ich weiss nicht ob da viel Thorie dahintersteckt. Jedenfalls stellt sich eben raus, dass knetische und potentielle Energie bei Kreisbahnen im verhältnis 1:2 stehen. Und das kann man ausnutzen - der Beweis wäre ohnehin trivial.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 22. Feb 2006 13:37 Titel: para Verfasst am: 22. Feb 2006 13:37 Titel: |
 |
|
Okay, klar. Ich war etwas verwirrt, weil du den Zwischenschritt weggelassen hattest. Aber so ist alles klar. Natürlich lässt sich das Verhältnis leicht nachweisen, aber dass das nützlich sein könnte muss einem in der Situation erstmal einfallen. ^^
Danke nochmal. :)
_________________
Formeln mit LaTeX |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 22. Feb 2006 13:54 Titel: as_string Verfasst am: 22. Feb 2006 13:54 Titel: |
 |
|
Hallo!
Die -1,5 war einfach nur so ein exemplarischer Wert für die Energie in diesem Potential. Die ganzen Zahlenwerte habe ich einfach mal so eingesetzt, um eine Kurve zu plotten. Die sind nicht berechnet und haben keinen Bezug zu Deiner Aufgabe.
Ich kann Dir aber mal schreiben, wie das mit dem effektiven Potential so ist (hoffentlich bekomme ich das noch richtig zusammen...) Eigentlich sollte das aber in Büchern über theoretische Mechanik alles drin stehen.
effektives Potential
Wenn man die Bewegung eines Körpers in einem Zentralpotential betrachtet, tut man das ja sinnigerweise gerne in Kugelkoordinaten. Dabei ist die Energie dann:
^2\right) = \frac{1}{2} m \dot{r}^2- \frac{\alpha}{r} + \frac{1}{2}mr^2\dot{\varphi}^2)
Wobei ich bei der Gravitation jetzt mal die Konstanten mit Alpha zusammengefasst habe.
Der (Betrag des) Drehimpuls in Kugelkoordinaten ist:

Und dieser Wert ist eine Erhaltungsgröße.
Deshalb kann man die Energie auch so schreiben:

Mit dem effektiven Potential:

Das heißt, dass man quasi einen Teil der kinetischen Energie zu dem Potential dazurechnen kann und dann nur noch ein eindimensionales Problem hat. Nur die Geschwindigkeit in radialer Richtung trägt dann noch zu der "neuen kinetischen Energie" bei und der Rest ist mit dem effektiven Potential erledigt. Wenn man jetzt so ne Kepplerellipse nimmt un nur den Radius in Abhängigkeit der Zeit aufmalt, dann entspricht das einer Bewegung eines Körpers genau in einem solchen effektiven Potential. Der Radius pendelt also dann immer hin und her. Zufällig beim Kepler-Potential und bei einem harmonischen-oszi-Potential mit der selben Frequenz wie die Umlaufzeit, so dass statische Bahnen entstehen. Bei anderen Potentialen ist das normalerweise nicht so, aber das ist für uns hier nicht wichtig.
Wenn man jetzt das maximale r kennt, dann kann man die Energie und den Drehimpuls ausrechnen und nach einem kleineren r suchen, bei dem dieses Potential den selben Wert hat. An der Energie siehst Du ja, dass dann der Term mit der Zeitableitung von r im Quadrat, also unsere neue kinetische Energie, dabei = 0 sein muß, weil ja die Gesamtenergie nach wie vor erhalten ist. Das heißt die beiden Extrempunkte für den Radius haben dann logischerweise auch eine 0 in der Ableitung des Radius nach der Zeit. So passt dann wieder alles wunderbar zusammen.
Du kannst jetzt also den Drehimpuls aus dem gegebenen v und r ausrechnen. Aus den Massen und r bekommst Du dann einen Wert für das effektive Potential. Wenn Du jetzt nach einem anderen r suchst, das bei identischem L auf das selbe effektive Potential kommt, dann hast Du den minimalen Radius gefunden und das ist der, den Du in der Aufgabe suchst. Allerdings weiß ich nicht, ob das nicht unnötig viel Aufwand ist. Das von schnudl und dermarkus erscheint etwas einfach zu rechnen zu sein, oder?
Gruß
Marco
Edit: Man nennt den Teil aus tangentialen Drehung, also das mit Drehimpuls und so, das Zentrifugalpotential, also das Potential, nur wenn Du das vielleicht nochmal irgendwo suchen willst...
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 22. Feb 2006 14:28 Titel: schnudl Verfasst am: 22. Feb 2006 14:28 Titel: |
 |
|
@as_string:
Das ist ja eine tolle Sache mit dem effektiven Potential ! Ich kenne das komischerweise aus der Quantenmechanik und der Streutheorie, aber mir war nie bewusst, dass dies (natürlich) auch klassisch gilt...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 22. Feb 2006 14:33 Titel: as_string Verfasst am: 22. Feb 2006 14:33 Titel: |
 |
|
Hallo schnudl!
Naja, um ehrlich zu sein wußte ich das auch nicht mehr, als ich die QM gehört habe, bis der Prof sagte, dass das ja genau so wie in der KM sei... Da hab' ich's dann nochmal nachgelesen, sonst wüßte ich das inzwischen sicher nicht mehr. Meine KM Vorlesung ist schon ziemlich lange her (so ungefähr 10 Jahre oder so...)
Gruß
Marco
Edit: Vielleicht nochmal kurz zu meinem Plot: Ich habe die Gerade da nur exemplarisch ein gezeichnet, um die konstante Energie an zu deuten. Die Differenz zwischen der Geraden und dem Potential ist dann das, was in "radialer kinetischer Energie" übrig bleibt, die an den Schnittpunkten gerade = 0 wird. Das ganze hat aber glaube ich mehr den Zweck, um solche Zentralpotentialbewegungen nochmal aus einem anderen Blickwinkel etwas anschaulicher zu machen. So sieht man schnell, dass für gebundene Zustände eben eine art Pendelbewegung im Radius zu erwarten ist, die unabhängig vom wirklichen Potential immer zu beobachten ist. Der Körper wird sich also auch bei anderen Potentialen innerhalb eines Ringes um das Zentrum bewegen. Auch für ungebundene Zustände (Streuzustände) kann man da ein paar Sachen aus dem eff. Potential lernen.
Im Allgemeinen finde ich das aber immer etwas gefährlich mit effektiven Potentialen und effektiven Massen und so weiter zu rechnen. Wenn man nicht genau weiß, was man tut, kommt man da schnell durcheinander finde ich. Man definiert ja auch in der Atomphysik für die äußeren Elektronen ein effektives Potential, das die Abschirmung der inneren Elektronen mit einbezieht. Das hat aber gar nichts mit diesem effektiven Potential hier zu tun, also bitte nicht verwechseln. Das hier ist ja eigentlich nur ein Einkörper Problem, das sich mit einer "reduzierten Masse" noch leicht auf ein Zweikörperproblem erweitern läßt. Das effektive Potential bei der Atomphysik ist aber dafür da, um ein Vielkörperproblem irgendwie in den Griff zu bekommen. Da fängt also die Verwirrung dann schon an...
Dass ich gerade auf ein effektives Potential zu sprechen komme, wundert mich selber irgendwie, weil ich das eben immer für etwas künstlich und gefährlich halte. Aber hier ist das denke ich wirklich recht anschaulich und auch zweckmäßig.
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 22. Feb 2006 16:53 Titel: para Verfasst am: 22. Feb 2006 16:53 Titel: |
 |
|
Danke dass du das mit dem Potential nochmal versucht hast mir näherzubringen. Ich glaube bis ich das so ganz verstanden habe wird es wohl noch ein bisschen dauern. ;)
Aber schön zu sehen dass es mal wieder mehr als einen Weg zum Ziel gibt. :)
_________________
Formeln mit LaTeX |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 22. Feb 2006 17:03 Titel: as_string Verfasst am: 22. Feb 2006 17:03 Titel: |
 |
|
Hallo para!
Eigentlich ist das nicht sooo schwer. Nur die Schreibweise ist wahrscheinlich etwas ungewohnt für Dich. Wenn Du möchtest, kann ich schon versuchen Dir das so zu erklären, dass Du es verstehst. Wenn Du mir sagst, an welchen Punkten Du mir nicht folgen konntest dann würden wir das sicher zusammen hin bekommen. Allerdings ist halt die Frage, ob Dir das zur Zeit überhaupt weiter hilft. Wenn es Dich aber trotzdem interessiert und Du ein wenig Zeit übrig hast, dann wäre ich froh, wenn ich Dir das erklären könnte.
Es liegt also bei Dir! 
Gruß
Marco
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 24. Feb 2006 10:19 Titel: para Verfasst am: 24. Feb 2006 10:19 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | Wenn es Dich aber trotzdem interessiert und Du ein wenig Zeit übrig hast, dann wäre ich froh, wenn ich Dir das erklären könnte. |
Ganz im Gegenteil, ich wollte deine erklärende Geduld hier nicht überstrapazieren, aber wenn dem so ist: gerne! Sonst hätte ich ja nicht gefragt. :)
Ich hab' mir das nochmal in Ruhe angesehen (sind ja schließlich Ferien ^^).
| as_string hat Folgendes geschrieben: | Wenn man die Bewegung eines Körpers in einem Zentralpotential betrachtet, tut man das ja sinnigerweise gerne in Kugelkoordinaten. Dabei ist die Energie dann:
^2\right) = \frac{1}{2} m \dot{r}^2- \frac{\alpha}{r} + \frac{1}{2}mr^2\dot{\varphi}^2)
Wobei ich bei der Gravitation jetzt mal die Konstanten mit Alpha zusammengefasst habe. |
Okay, so weit kann ich folgen.
| as_string hat Folgendes geschrieben: | Der (Betrag des) Drehimpuls in Kugelkoordinaten ist:

Und dieser Wert ist eine Erhaltungsgröße. |
Die Betrachtung des Betrags des Drehimpulses kann man sich hier mit diesem "normalen Produkt" vereinfachen weil wir uns in Kugelkoordinaten bewegen, oder? Denn wie wir ja festgestellt hatten, gilt diese Betrachtung in karthesischen Koordinaten nur am Perihel und am Aphel.
| as_string hat Folgendes geschrieben: | Deshalb kann man die Energie auch so schreiben:

Mit dem effektiven Potential:
 |
Okay. Mit dem Kniff des Erweiterns um mr² nachzuvollziehen.
| as_string hat Folgendes geschrieben: | | Das heißt, dass man quasi einen Teil der kinetischen Energie zu dem Potential dazurechnen kann und dann nur noch ein eindimensionales Problem hat. Nur die Geschwindigkeit in radialer Richtung trägt dann noch zu der "neuen kinetischen Energie" bei und der Rest ist mit dem effektiven Potential erledigt. |
Diesen Trick mit dem effektiven Potential verstehe ich nicht. Okay, die mathematische Definition ist klar, man ergänzt das normale Potential durch die vom Drehimpuls bedingte Komponente, aber was sagt das jetzt aus?
| as_string hat Folgendes geschrieben: | Wenn man jetzt so ne Kepplerellipse nimmt un nur den Radius in Abhängigkeit der Zeit aufmalt, dann entspricht das einer Bewegung eines Körpers genau in einem solchen effektiven Potential. Der Radius pendelt also dann immer hin und her. [...]
Wenn man jetzt das maximale r kennt, dann kann man die Energie und den Drehimpuls ausrechnen und nach einem kleineren r suchen, bei dem dieses Potential den selben Wert hat. An der Energie siehst Du ja, dass dann der Term mit der Zeitableitung von r im Quadrat, also unsere neue kinetische Energie, dabei = 0 sein muß, weil ja die Gesamtenergie nach wie vor erhalten ist. Das heißt die beiden Extrempunkte für den Radius haben dann logischerweise auch eine 0 in der Ableitung des Radius nach der Zeit. So passt dann wieder alles wunderbar zusammen. |
Also die Vorgehensweise ist klar, aber warum betrachtet man dabei jetzt gerade dieses effektive Potential? Bzw. warum können wir den "drehimpulshaltigen" Teil zu diesem Potential hinzuzählen und den kinetischen nicht? Dieser logische Schritt ist mir irgendwie noch nicht ersichtlich. Wahrscheinlich liegt es daran, dass ich noch nicht wirklich tief in die theoretische Mechanik eingestiegen bin und deshalb noch keine richtige Vorstellung von der Definition des Potentials habe. Könntest du den Gedanken vielleicht nochmal ein bisschen genauer ausführen?
_________________
Formeln mit LaTeX |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. Feb 2006 11:17 Titel: dermarkus Verfasst am: 24. Feb 2006 11:17 Titel: |
 |
|
| para hat Folgendes geschrieben: |
| as_string hat Folgendes geschrieben: | Der (Betrag des) Drehimpuls in Kugelkoordinaten ist:

Und dieser Wert ist eine Erhaltungsgröße. |
Die Betrachtung des Betrags des Drehimpulses kann man sich hier mit diesem "normalen Produkt" vereinfachen weil wir uns in Kugelkoordinaten bewegen, oder? Denn wie wir ja festgestellt hatten, gilt diese Betrachtung in karthesischen Koordinaten nur am Perihel und am Aphel.
|
An dieser Stelle war nur ein Zwischenschritt ungenau formuliert; genau heißt es:

So gilt das also für alle Punkte der Ellipsenbahn; das Ergebnis für L ist nach wie vor richtig und kann damit weiterverwendet werden.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 24. Feb 2006 19:48 Titel: as_string Verfasst am: 24. Feb 2006 19:48 Titel: |
 |
|
Hallo!
Aber wir erklären doch gerne, besonders wenn wir ein interessiertes "Opfer" gefunden haben 
Ja, da war ich etwas ungenau beim Drehimpuls. So, wie das dermarkus geschrieben hat, ist das schon mal viel besser!
Aber sonst hast Du doch so ziemlich alles kapiert, so weit. Das ist doch schon mal sehr gut! Vielleicht noch mal etwas als Hintergrund, den Du wahrscheinlich noch nicht wissen kannst: In der Quantenmechanik spielt ja immer der Hamilton-Operator eine wichtige Rolle. Mit diesem Operator kann man auch die Energie eines Systems berechnen. Es gibt auch in der klassischen Mechanik einen Hamiltonsches Prinzip. In der QM ist es zumindest so, dass wenn man den Hamilton-Operator eines Systems kennt, die gesamte Dynamik etc. dieses Systems ausrechnen kann (zumindest bei Einteilchen-Systemen und bei nicht explizit zeitabhängigen Potentialen... genau weiß ich's jetzt nicht mehr...). So weit ich mich dunkel erinnern kann, ist das in der KM dann auch so. Muß ja auch so sein, weil die QM in großen Bereichen in die KM übergeht. Leider müßte ich jetzt selber das nochmal lesen, um Dir das genauer beschreiben zu können.
Aber warum macht man das mit diesem Potential jetzt aber? Erstmal ist das wirklich nur ein mathematischer Trick. Aber man sucht ja nach Möglichkeiten Bewegungen in einem Zentralpotential berechnen zu können, weil das ja recht häufig auftritt, nicht nur beim Keppler-Potential. Und mit dem effektiven Potential hat man die Möglichkeit, die zweidimensionale Bewegung "rein mathematisch" auf eine eindimensionale zu reduzieren. Man muß also nur noch die Bewegungsgleichungen für eine Bewegung im effektiven (eindimensionalen) Potential berechnen und nicht mehr mit den komplizierten Elipsen, die ja bei anderen Zentralpotentialen nicht mehr unbedingt Elipsen sein müssen.
Wie kommt man aber überhaupt auf diese Aufteilung? Allgemein kannst Du ja eine Energie immer als Summe von potentieller Energie und kinetischer Energie berechnen. Was genau ist aber potentielle und kinetische Energie? Nunja, potentielle Energie ist alles das, was nur vom Ort abhängt und kinetische das, was von der Geschwindigkeit abhängt, also von der zeitlichen Ableitung (der Änderung) des Ortes. Wenn man jetzt weiß, dass der Drehimpuls erhalten ist, kommt man recht schnell auf die Idee, dass man ja den tangentialen Anteil der kinetischen Energie auch mit dem Drehimpuls ausdrücken kann, was ich ja auch gemacht habe. Wenn man das macht, hat man immer noch erstmal 3 Terme, bei denen aber nur noch einer von einer zeitlichen Ableitung einer Koordinate abhängt und die anderen beiden nur noch von der Koordinate direkt. Noch besser: Es bleibt nur noch eine Koordinate übrig! Nämlich r und Phi ist "weg". Deshalb liegt es dann eben nahe, die Energie neu aufzuteilen, in eine neue potentielle Energie (daraus das effektive Potential) und eine neue kinetische Energie. Damit kann man dann sogar Bewegungsgleichungen lösen! Man hat ja die selbe Formel (für die Energie) wie für eine eindimensionale Bewegung in genau einem solchen Potential. Du kannst Dir das vielleicht als Hügellandschaft vorstellen, aber das wäre eigentlich genau genommen schon wieder ein mehrdimensionales Problem. Jedenfalls könnte man sich ja leicht eine solche gebogene Bahn vorstellen, wie ich sie geplottet, habe und reibungsfrei einen Körper darauf hin und her pendeln lassen. Nur muß das ganze möglichst flach sein, damit man das näherungsweise noch als 1-dim. Problem auffassen kann...
Bei einer solchen Bewegung ist aber klar, dass der Körper sich immer innerhalb der Grenzen bewegen muß, bei denen das Potential noch kleiner oder gleich der Gesamtenergie des Körper ist. So sieht man dann schon mal leicht, dass er sich auf einem Ring um das Zentrum aufhalten muß, weil der Radius immer in einem bestimmten Bereich liegen muß. Außerdem sieht man, dass selbst bei einem ungebundenen Zustand, also bei dem die Gesamtenergie >0 ist, nicht an das Zentrum zu nahe ran kommt, weil das Zentrifugalpotential sonst zu groß wird. Allerdings eben nur, wenn der Drehimpuls nicht gegen 0 geht. Meine Idee war jetzt, dass man das Potential aus den gegebenen Werten ja berechnen kann und die Gesamtenergie auch gegeben hat. So kann man dann auch die beiden Wendepunkte in diesem Potential ausrechnen, die dann dem maximalen und minimalen Radius entsprechen.
Willst Du das vielleicht mal probieren? Dabei lernst Du wahrscheinlich schon ein wenig was... Ich war bis jetzt zu faul, aber will das bei Gelegenheit auch nochmal rechnen.
Gruß
Marco
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 25. Feb 2006 17:49 Titel: para Verfasst am: 25. Feb 2006 17:49 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | Wie kommt man aber überhaupt auf diese Aufteilung? Allgemein kannst Du ja eine Energie immer als Summe von potentieller Energie und kinetischer Energie berechnen. Was genau ist aber potentielle und kinetische Energie? Nunja, potentielle Energie ist alles das, was nur vom Ort abhängt und kinetische das, was von der Geschwindigkeit abhängt, also von der zeitlichen Ableitung (der Änderung) des Ortes. |
Der Satz war wichtig. Die Unterscheidung nach den Kriterien war mir noch nicht ganz klar. Ich hab' den und den ersten Ansatz mal durchgerechnet.
Die Aufgabe war allgemein gestellt, aber ich hab' einfach mal ein paar Werte angenommen.
Annahmen für die Ausgangslage (kurz nach dem Abbremsen):


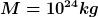
Der (korrigierte) Ansatz den ich zuerst verfolgt habe:


Liefert dann neben der Ausgangsposition die weitere Lösung:


Dein Ansatz mit dem Potential sieht ja dann so aus:
 - \gamma \cdot M \cdot m / r = L^2/(2 \cdot m \cdot r') - \gamma \cdot M \cdot m / r')

Und hat ebenfalls die beiden Lösungen:


Und die entsprechenden Geschwindigkeiten dazu.
Klappt also alles wunderbar. Tolle Sache das. 
Danke für die Erklärungen. Ich denke die Aufgabe ist damit hinreichend gelöst.
_________________
Formeln mit LaTeX |
|
 |
|
|