| Autor |
Nachricht |
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
 Geco Verfasst am: 01. Dez 2015 16:48 Titel: Veränderung des Drehmoments bei Kardanwellen |
 |
|
Hallo Leute,
ich würde gern wissen, wie man das nötige Drehmoment an einer Kardanwelle berechnet, welche mit mehereren Gliedern verlängert wurde, jedoch nicht nur vertikal, sondern auch einen Winkel drin hat.
Beispiel: Die Welle wird auf Erdbodenhöhe gedreht und führt durch einen Schacht ins Erdreich über 5 Glieder und das letzte ist um 30° abgewinkelt, wo dann eine Armatur betätigt wird.
Wie muss ich den Verlust an Drehmoment an der Abwinklung berechnen um zu wissen wie viel ich oben anbringen muss. Das max. Drehmoment der Armatur ist bekannt.
Vielen Dank
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 01. Dez 2015 17:43 Titel: |
|
|
|
Bitte eine Skizze!
|
|
|
jmd
Anmeldungsdatum: 28.10.2012
Beiträge: 577
|
| jmd Verfasst am: 01. Dez 2015 18:30 Titel: |
|
|
Mir scheint das so
Für den Eingang gilt
Am Ausgang
wenn man die Reibung vernachlässigen hat man das gleiche Drehmoment
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 02. Dez 2015 09:01 Titel: |
|
|
| jmd hat Folgendes geschrieben: | Mir scheint das so
Für den Eingang gilt
Am Ausgang
wenn man die Reibung vernachlässigen hat man das gleiche Drehmoment |
Bei einem einfachen Kardangelenk ist, abhängig vom Achsenwinkel
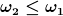
Ein Umlenkungswinkel von  ist grenzwertig.
Das gleiche gilt für das Drehmoment.
Dieser Effekt lässt sich durch 2 serielle Kardangelenke ausgleichen.
Die beste Lösung ist ein homokinetisches Gelenk.
|
|
|
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
| Geco Verfasst am: 03. Dez 2015 14:27 Titel: |
|
|
Hier die gewünschte Skizze
 http://i.imgur.com/S9Ruy1A.jpg
Wie gesagt gewollt ist das Drehmoment das man im Punkt 1 aufbringen muss um im Punkt 2 die Armatur betätigen zu können, da bei dem Winkel + Reibung was verloren geht. Die Kraft wird per Hand aufgebracht, also kein Motor
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 03. Dez 2015 17:10 Titel: |
|
|
| Geco hat Folgendes geschrieben: | Hier die gewünschte Skizze
http://i.imgur.com/S9Ruy1A.jpg
Wie gesagt gewollt ist das Drehmoment das man im Punkt 1 aufbringen muss um im Punkt 2 die Armatur betätigen zu können, da bei dem Winkel + Reibung was verloren geht. Die Kraft wird per Hand aufgebracht, also kein Motor |
Mit Winkel der Welle zwischen den Kardangelengen und Drehwinkerl 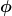 der Eingangswelle
 }{1- \cos ^{2} (\phi)\cdot \sin^{2} (\beta) } )
Das Drehmoment an der Abtriebswelle ist also nicht konstant, sondern schwankt
mit dem Drehwinkel der Eingangswelle.
|
|
|
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
| Geco Verfasst am: 03. Dez 2015 18:00 Titel: |
|
|
Welche Werte nimmt φ an? Ich kann mir im Praktischen nicht vorstellen was er darstellt. Sind das im Prinzip die Umdrehungen im Punkt 1? Sorry ist leider gar nicht meine Fach.
Vielen Dank bisher
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 03. Dez 2015 18:39 Titel: |
|
|
| Geco hat Folgendes geschrieben: | Welche Werte nimmt φ an? Ich kann mir im Praktischen nicht vorstellen was er darstellt. Sind das im Prinzip die Umdrehungen im Punkt 1? Sorry ist leider gar nicht meine Fach.
Vielen Dank bisher |
Das ist der Winkel mit dem Du die Eingangswelle drehst.
Eine Umdrehung = 
|
|
|
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
| Geco Verfasst am: 03. Dez 2015 19:35 Titel: |
|
|
|
D.h wenn ich die Formel nach M1 umstelle, weiß ich wie viel Drehmoment ich oben anbringen muss. Aber Winkel φ wäre ja trozdem unbekannt, weil ich nicht wissen kann wie viel Umdrehungen ich brauche, bis die Armatur geschlossen ist. Oder wäre das ein empirischer Wert den man mal aus einem Test feststellen muss?
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 03. Dez 2015 19:44 Titel: |
|
|
| Geco hat Folgendes geschrieben: | | D.h wenn ich die Formel nach M1 umstelle, weiß ich wie viel Drehmoment ich oben anbringen muss. Aber Winkel φ wäre ja trozdem unbekannt, weil ich nicht wissen kann wie viel Umdrehungen ich brauche, bis die Armatur geschlossen ist. Oder wäre das ein empirischer Wert den man mal aus einem Test feststellen muss? |
Das Drehmoment = Kraft x Hebelarm hat nichts mit der Anzahl der Umdrehungen zu tun.
Da sich die Kraft abhängig vom Drehwinkel der Antriebswelle nach einer Sinusfunktion verändert, ändert sich auch das Drehmoment. Dieser Zyklus wiederholt sich bei jeder Umdrehung.
In der anhängenden Graphik ist der Drehzahl und Momentenverlauf in Abhängigkeit vom Drehwinkel phi und dem Winkel der Kardanwelle Beta dargestellt.
Jetzt müßte eigentlich alles klar sein.
| Beschreibung: |
|
Download |
| Dateiname: |
Kardangelenk.pdf |
| Dateigröße: |
51.37 KB |
| Heruntergeladen: |
461 mal |
|
|
|
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
| Geco Verfasst am: 03. Dez 2015 21:54 Titel: |
|
|
Vielen vielen Dank. 
|
|
|
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
| Geco Verfasst am: 14. Dez 2015 10:05 Titel: |
|
|
|
wird bei mehreren abwinklungen eigentlich einfach mit Faktor zwei multipliziert sofern der Winkel gleich ist? Und wenn nicht einfach nochmal das Moment mit neuem Winkel errechnet und zum ersten Moment addiert?
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 14. Dez 2015 11:24 Titel: |
|
|
| Geco hat Folgendes geschrieben: | | wird bei mehreren abwinklungen eigentlich einfach mit Faktor zwei multipliziert sofern der Winkel gleich ist? Und wenn nicht einfach nochmal das Moment mit neuem Winkel errechnet und zum ersten Moment addiert? |
So einfach ist das nicht bei einem gekoppelten Gelenkstrang. Der ungleichförmige abtriebsseitige Momentenverlauf der ersten Gelenkwelle ist das ungleichförmige Eingangsmoment für die zweite Gelenkwelle.
Der abtriebseitige Momentenverlauf des Gesamtstrangs hängt von den Eingangstellungen der Kreuzgelenke ab.
Das im Einzelnen auszuführen, sprengt m. E. hier den Rahmen
|
|
|
Geco
Anmeldungsdatum: 01.12.2015
Beiträge: 7
|
| Geco Verfasst am: 15. Dez 2015 16:48 Titel: |
|
|
|
Für meine Anwendung ist es nur noch wichtig eine weitere Abwinklung zu berechnen. Muss ich da meine gegebene Formel mit dem Ungleichförmigkeitsgrad erweitern?
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 15. Dez 2015 17:29 Titel: |
|
|
| Geco hat Folgendes geschrieben: | | Für meine Anwendung ist es nur noch wichtig eine weitere Abwinklung zu berechnen. Muss ich da meine gegebene Formel mit dem Ungleichförmigkeitsgrad erweitern? |
Wie ich schon sagte, ist die Berechnung gekoppelter Gelenkwellen nicht trivial und geht über den Rahmen des Forums und meine Zeit hinaus.
Wende Dich an einen Ingenieur, einen Hersteller von Gelenkwellen, eine FH oder eine Uni/TH.
|
|
|
|
Registrieren
Login
FAQ
Suchen
