| Autor |
Nachricht |
aryx5d
Anmeldungsdatum: 31.05.2016
Beiträge: 4
|
 aryx5d Verfasst am: 31. Mai 2016 23:42 Titel: Zeitliche Veränderung von Heizwiderständen |
 |
|
Hallo liebe Physiker!
Für meine Bachelorarbeit in Mathematik möchte ich ein Modell für die Veränderung eines Heizwiderstandes an einer konstanten Spannungsquelle nach der Zeit aufstellen. Leider gibt es für mich einige Unklarheiten bzgl. der elektrotechnischen Grundlagen.
Kurz die wichtigsten Einzelheiten:
1. Die Schaltung ist ganz einfach: An einer Batterie liegt eine Heizwendel an.
2. Die Spannung an der Batterie wird als konstant angenommen und ist bekannt.
3. Der Widerstand der Heizwendel ist bei Raumtemperatur gegeben.
4. Das Material und damit der lineare Temperaturkoeffizient und die spezifische Wärmekapazität der Heizwendel sowie ihre Masse ist bekannt.
Ich suche nach eine Funktion R(t) für den Widerstand der Heizwendel nach der Zeit.
Bekannt ist mir:
1. Für den Widerstand nach der Temperatur gilt:
 = R(T_{0}) \cdot (1 + \alpha_{T_{0}} \cdot (T-T_{0}))
<br />
)
mit  : lin. Temperaturkoeffizienten.
2. Für die Veränderung der Temperatur gilt:
mit m: Masse und c: spez. Wärmekapazität.
3. Für die Wärmeenergie bei einer zeitveränderlichen Leistung P(s) (welche durch den Anstieg des Widerstandes zu erwarten ist) gilt:
=\int_0^t \! P(s) \, \dd s
<br />
)
.
Damit war ich eigentlich ziemlich glücklich. Allerdings habe mich glaube ich versehen und in 1. ) durch 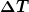 ersetzt. Dadurch konnte ich dann 2. in 1. einsetzen und dann nur noch Q für das Integral aus 3. ersetzen.
Mit  = R(t) = \frac{U^2}{P(t)} ) aus dem ohmschen Gesetz könnte ich dann nach Umformung aufstellen:
} = \frac{m \cdot c}{\alpha_{T_{0}}} \cdot P(t) + P(t) \cdot \int_0^t \! P(s) \, \dd s)
was ich nach einer Lösung für P(t) untersuchen könnte um mit dem ohmschen Gesetz dann die Funktion R(t) zu erhalten.
Hat jemand eine Idee, wie ich 2. mit 1. vereinbart bekomme? Über Literaturtipps würde ich mich auch sehr freuen!
P.S. (Ist mir beim Schreiben aufgefallen!):
In 2. ist mir das 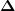 vor dem Q auch verloren gegangen. Aber kann ich damit nicht sagen:
Ich nehme an, dass die Funktionen Q(t) und T(t) existieren und damit gilt:
 - Q(t_{1})) und  - T(t_{1}))
und somit für 2.:
 - T(t_{1}) = \frac{1}{m \cdot c} \cdot ( Q(t_{2}) - Q(t_{1}))
<br />
)
Teile ich dann beide Seiten durch  und betrache den Grenzwert für minimal kleine Zeiträume, dann erhalte ich doch die Ableitungen und somit:
 = \frac{Q'(t)}{m \cdot c}
<br />
)
Dann integriere ich nach der Zeit und erhalte somit
 = \frac{Q(t)}{m \cdot c}
<br />
)
Von dort aus könnte ich dann fast unverändert weitermachen und hätte nur einen weiteren Term, der durch das  in 1. entsteht, zu berücksichtigen, der aber auch konstant bleibt.
Kann mir das jemand bestätigen? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 31. Mai 2016 23:54 Titel: |
|
|
|
Wie beschreibst Du die Wärmeabgabe bei wechselnden Temperaturen? |
|
|
aryx5d
Anmeldungsdatum: 31.05.2016
Beiträge: 4
|
| aryx5d Verfasst am: 01. Jun 2016 00:19 Titel: |
|
|
|
Ich weiß nicht ob ich die Frage korrekt verstehe. Meinst du die Abgabe der Wärmeenergie der Heizwendel an die Umgebung? Die vernachlässige ich. Für die Bachelorarbeit in Mathe reicht ein stark idealisiertes Modell. Genau so vernachlässige ich auch die unterschiedliche Hitze an den verschiedenen Punkten der Heizwendel. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 01. Jun 2016 09:31 Titel: |
|
|
|
Mir fällt dazu nichts (höfliches) ein. |
|
|
aryx5d
Anmeldungsdatum: 31.05.2016
Beiträge: 4
|
| aryx5d Verfasst am: 01. Jun 2016 09:39 Titel: |
|
|
|
Das ist schade. Ich habe mit Physik nichts am Hut und studiere Mathematik auf Lehramt, dementsprechend habe ich nur Kenntnisse über die Grundveranstaltungen der Mathematik und nicht den Blassesten von Elektrotechnik. Vielleicht könntest du ja diese Information in eine höfliche Antwort einfließen lassen. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 10:19 Titel: |
|
|
|
Ich versteh nicht ganz Dein Problem, Du hast doch alle Formeln da die Du brauchst (oder überseh ich hier irgendwas?)... |
|
|
aryx5d
Anmeldungsdatum: 31.05.2016
Beiträge: 4
|
| aryx5d Verfasst am: 01. Jun 2016 13:08 Titel: |
|
|
|
Ich wusste zuerst nicht, wie ich mit den 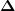umgehen soll. Beim Schreiben der Frage ist mir dann der untere Ansatz in den Sinn gekommen bei dem ich mir aber nicht sicher (und nach franzs Antwort auch enorm unsicher) bin, ob ich das alles so machen darf. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 13:20 Titel: |
|
|
Das Delta was Dich vermutlich verwirrt ist das Delta beim Q. Da bezeichnet es nämlich keine Differenz wie sonst üblich, das die Wärme keine Zustandsgröße ist, die zu jedem Zeitpunkt einen Wert hat, sondern schlicht für die Energie steht die zwischen Systemen übertragen wird (hier elektrischer Strom erhitzt den Widerstand). D.h. das Q in der Integralformel mit dem P sollte auch ein Delta Q sein.
PS: Dein "Trick" mit dem Ableiten und dann integrieren ist im übrigen falsch. Du hast die Integrationskonstante vergessen. Daher funktioniert das auch nicht. |
|
|
aryx5du
Gast
|
| aryx5du Verfasst am: 01. Jun 2016 13:59 Titel: |
|
|
Hab Dank! Das Delta vor dem Q hat mich in der Tat verwirrt. Das Delta vor dem T aber auch. Liege ich richtig, dass dieses Gesetz beschreibt, wie eine "Einspeisung" von Wärmeenergie in ein Objekt sich auf die Temperaturdifferenz auswirkt?
Dann weiß ich aber nicht, wie ich
so umformen kann, dass ich in
für T ersetzen darf.
Denke ich überhaupt prinzipiell in die richtige Richtung, wenn ich so weit Gesetze in die Formel für den Widerstand nach der Temperatur einsetze, dass ich am Ende auf eine Funktion für die Leistung oder den Widerstand nach der Zeit stoße?
Ich habe im Vornherein auch eigentlich angenommen, dass ich eine DGL finden würde. Irgendwie sieht das momentan aber nicht so aus. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 14:06 Titel: |
|
|
| aryx5du hat Folgendes geschrieben: | | Hab Dank! Das Delta vor dem Q hat mich in der Tat verwirrt. Das Delta vor dem T aber auch. Liege ich richtig, dass dieses Gesetz beschreibt, wie eine "Einspeisung" von Wärmeenergie in ein Objekt sich auf die Temperaturdifferenz auswirkt? |
Ja.
Und genauso beschreibt die andere Gleichung wie sich eine Temperaturdifferenz auf den Widerstand auswirkt.
| Zitat: |
Denke ich überhaupt prinzipiell in die richtige Richtung, wenn ich so weit Gesetze in die Formel für den Widerstand nach der Temperatur einsetze, dass ich am Ende auf eine Funktion für die Leistung oder den Widerstand nach der Zeit stoße?
|
Ja.
| Zitat: |
Ich habe im Vornherein auch eigentlich angenommen, dass ich eine DGL finden würde. Irgendwie sieht das momentan aber nicht so aus. |
Da die Leistung vom Widerstand abhängt wirst Du dann erstmal eine Integralgleichung erhalten, die Du in eine DGL überführen kannst. |
|
|
aryx5du
Gast
|
| aryx5du Verfasst am: 01. Jun 2016 14:27 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: |
Und genauso beschreibt die andere Gleichung wie sich eine Temperaturdifferenz auf den Widerstand auswirkt. |
Aber ist das hier problematisch, dass die Formel für den Widerstand nach der Temperatur die Temperaturdifferenz relativ zu T0=20°C erfordert? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 14:28 Titel: |
|
|
| aryx5du hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: |
Und genauso beschreibt die andere Gleichung wie sich eine Temperaturdifferenz auf den Widerstand auswirkt. |
Aber ist das hier problematisch, dass die Formel für den Widerstand nach der Temperatur die Temperaturdifferenz relativ zu T0=20°C erfordert? |
Problematisch sicherlich nicht. Wenn Du es für zwei andere Temperaturen willst, musst Du halt ein wenig ergänzen... |
|
|
aryx5du
Gast
|
| aryx5du Verfasst am: 01. Jun 2016 15:03 Titel: |
|
|
Ich komme leider nicht drauf.
Wenn ich den Widerstand von Delta T abhängig machen will, dann muss sich doch auch der lineare Temperaturkoeffizient ändern, denn der bezieht sich doch nur auf Temperaturdifferenz zu T0, oder nicht? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 15:33 Titel: |
|
|
|
T-T0 = T-T1 + T1-T0 |
|
|
aryx5du
Gast
|
| aryx5du Verfasst am: 01. Jun 2016 16:27 Titel: |
|
|
Vielen Dank, war blind!
Aber wenn ich dann eine der beiden Differenzen durch Delta T ersetze, dann bleibt meine Gleichung doch noch immer von einer Temperatur T1 abhängig. Kann ich T1 dann anders ausdrücken? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 16:30 Titel: |
|
|
| aryx5du hat Folgendes geschrieben: |
Aber wenn ich dann eine der beiden Differenzen durch Delta T ersetze, dann bleibt meine Gleichung doch noch immer von einer Temperatur T1 abhängig. Kann ich T1 dann anders ausdrücken? |
Du musst schon wissen was für eine Situation Du beschreiben willst, sprich bei welchem T1 Du starten musst... |
|
|
aryx5du
Gast
|
| aryx5du Verfasst am: 01. Jun 2016 16:43 Titel: |
|
|
|
Ah ok. Kann ich also annehmen, das T1 konstant gegeben ist als wirklich aktuelle Temperatur des Widerstandes, kurz bevor die Spannungsquelle eingeschaltet wird? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 01. Jun 2016 16:45 Titel: |
|
|
| aryx5du hat Folgendes geschrieben: | | Ah ok. Kann ich also annehmen, das T1 konstant gegeben ist als wirklich aktuelle Temperatur des Widerstandes, kurz bevor die Spannungsquelle eingeschaltet wird? |
Ich hab keine Ahnung was Du annehmen kannst... das ist doch Deine Arbeit... |
|
|
|
Registrieren
Login
FAQ
Suchen
