| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17264
|
 TomS Verfasst am: 29. Nov 2014 23:16 Titel: FAQ - gravitative, kosmologische und Doppler-Rotverschiebung |
 |
|
Ich möchte im Folgenden eine minimalistische Darstellung der Rotverschiebung präsentieren, wobei Dopplerverschiebung, gravitative sowie kosmologische Rotverschiebung für Spezialfälle aus einer vereinheitlichten Formel folgen. Dabei werde ich keinerlei spezielle Voraussetzung bzgl. Koordinatensystemen, Beobachtern oder Symmetrien der Raumzeit annehmen.
Meine Schlussfolgerung ist, dass die Unterscheidung bzw. Trennung der Effekte wie kinematische Dopplerverschiebung, gravitative und kosmologische Rotverschiebung nur in Spezialfällen, d.h. für spezielle Raumzeiten mit bestimmten Symmetrien sowie für spezielle Beobachter möglich ist. Im allgemeinen ist eine derartige Interpretation nicht sinnvoll und physikalisch auch nicht notwendig.
Ich definiere zunächst die lokal messbare Frequenz omega gemäß
 = u_\mu k^\mu)
u bezeichnet dabei die Vierergeschwindigkeit eines Beobachters, k den Wellenvektor des Photons (bzw. der el.-mag. Welle lokal am Ort des Beobachters). Dieser Ausdruck wird für den Ort der Quelle i = 1 sowie des Empfängers i = 2 für zwei jeweils dort befindliche Beobachter ausgewertet.
Die Rotverschiebung z ist dann gegeben als
}{(u_2,k_2)})
Diese Definition beinhaltet automatisch den kinematischen Dopplereffekt, wenn nämlich der Quotient für zwei verschiedene Beobachter mit unterschiedlicher Vierergeschwindigkeit u am selben Punkt der Raumzeit ausgewertet wird.
Quelle und Empfänger sind durch eine lichtartige Geodäte (= die Bahnkurve des Photons durch die Raumzeit) verbunden. Die Frage ist nun, wie sich der Wellenvektor k des Photons entlang der Geodäten x ändert. Geometrisch folgt dies aus der Parallelveschiebung. Physikalisch argumentiert man, dass k den Wellenvektor einer ebenen Welle beschreibt, deren Ausbreitungsrichtung lokal in Richtung der Geodäten erfolgt, wobei k auf den Wellenfronten senkrecht steht. Letzteres müsste prinzipiell aus einer Näherung der Einstein-Maxwell-Gleichungen abgeleitet werden. Ich denke, die physikalisch sinnvolle Voraussetzung ist, dass die Wellenlänge entlang der Geodäten stets klein gegen die typische Krümmung ist.
Ich definiere den Zusammenhang A, die kovariante Richtungsableitung D sowie die Parallelverschiebung von k mittels der Christoffel-Symbole Gamma
^\mu = \dot{k}^\mu - A^\mu_\rho \, k^\rho = 0)
entlang der Geodäten x
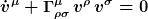
wobei v die Geschwindigkeit (Ableitung) bzgl. des affinen Parameters entlang x bezeichnet
)
Nun erfüllt x eine lichtartige Geodätengleichung, und der Wellen- bzw. Impulsvektor k eines Photons entlang x ist immer parallel zum Geschwindigkeitsvektor v. D.h. es gilt
für eine zunächst unbestimmte Konstante kappa.
Da x die Geodätengleichung löst, ist v außerdem eine spezielle Lösung der Gleichung zur Parallelverschiebung (es handelt sich um die Parallelverschiebung des Tangentenvektors v an x). Diese Gleichung ist aber linear im zu verschiebenden Vektor, d.h. mit v ist auch
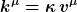
eine Lösung zur Parallelverschiebung (nicht jedoch der Geodätengleichung).
Für die Frequenz folgt also
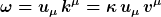
Die Konstante kappa fällt bei der Bildung des Quotienten heraus und es gilt
}{(u_2,k_2)} = \frac{(u_1,v_1)}{(u_2,v_2)})
Daraus folgt, dass die Rotverschiebung z alleine durch die lokal definierten Vierergeschwindigkeiten u zweier Beobachter i = 1,2 sowie die lichtartige Geodäte x bzw. den Tangentenvektor v gegeben ist. Letzterer kodiert die Effekte der Raumzeitkrümmung.
Interessant ist auch, dass z unabhängig von kappa, also von der ursprünglichen Frequenz ist, d.h. unabhängig davon, ob wir kurz- oder langweiliges Licht betrachten.
Die Schlussfolgerung, dass die Interpretation der Rotverschiebung mittels einzelner Effekte wie kinematischer Dopplerverschiebung, gravitativer und kosmologischer Rotverschiebung im allgemeinen nicht sinnvoll und physikalisch auch nicht notwendig ist, sondern lediglich in Spezialfällen, d.h. für spezielle Raumzeiten mit bestimmten Symmetrien sowie für spezielle Beobachter möglich ist, folgt aus der Tatsache, dass
1) die definierende Gleichung für z nicht ohne die Vierergeschwindigkeiten u formulierbar ist, d.h. dass man die kinematischen Effekte prinzipiell nicht abspalten oder eliminieren kann, und dass
2) die Raumzeitgeometrie nur implizit in der Geodäten x bzw. der lichtartigen Tangente v kodiert ist (und daraus, dass ein Gravitationspotential U bzw. ein Skalenfaktor a(t) nur für bestimmte Spezialfälle der Raumzeit definiert werden können).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Nov 2016 16:17, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17264
|
| TomS Verfasst am: 09. Dez 2014 00:46 Titel: |
|
|
Ich möchte nun für drei Fälle die Berechnung skizzieren
Kinematischer Dopplereffekt
Wir betrachten einen bzgl. der Lichtquelle ruhenden i=1 sowie einen sich bewegenden Beobachter i=2. Dann gilt
)
 = \gamma\,(1,u\hat{e}_2))
)
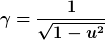
Man überprüft sofort
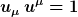
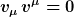
Für den Winkel zwischen dem Dreiervektor der Geschwindigkeit des zweiten Beobachters sowie der Ausbreitungsrichtung des Lichtsignals definiert man
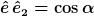
Damit ist
 = 1)
 = \frac{1-u\,\cos\alpha}{\sqrt{1-u^2}})
Daraus folgen die Formeln für den longitudinalen sowie transversalen Dopplereffekt
_________________
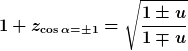
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17264
|
| TomS Verfasst am: 09. Dez 2014 01:05 Titel: |
|
|
Gravitationsrotverschiebung in der Schwarzschildlösung
Wir betrachten zwei ruhende Beobachter i=1,2 im Außenraum eines gravitierenden Körpers der Masse M mit Schwarzschildradius
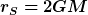
Die Schwarzschildmetrik lautet
\,dt^2 - f^{-1}(r)\,dr^2 - r^2\,d\Omega^2)
 = 1 - \frac{r_S}{r})
Wir betrachten rein radiale Lichtstrahlen, d.h. wir benötigen nur die t- sowie die r-Komponente der Metrik
)
Für radiale, lichtartige Geodäten gilt
})
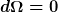
Daraus folgt
,r))
,1))
Für die Vierergeschwindigkeit eines bei r ruhenden Beobachters in der Schwarzschildgeometrie gilt
,0))
und daraus folgt
 = \frac{1}{\sqrt{f(r_i)}})
und damit die Gravitationsrotverschiebung
}{f(r_1)}})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17264
|
| TomS Verfasst am: 09. Dez 2014 01:34 Titel: |
|
|
Kosmologische Rotverschiebung im FRW-Universum
Wir betrachten zwei mitbewegte Beobachter i=1,2 in der FRW-Metrik mit zunächst beliebigem Skalenfaktor a(t). Die Metrik lautet
\,(dr^2 + r^2\,d\Omega^2))
Wir betrachten wiederum radiale Lichtstrahlen, d.h.
))
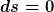
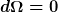
mit
} = dr)
Daraus folgt
,1))
Für die Vierergeschwindigkeit eines mitbewegten Beobachters in der FRW-Geometrie gilt
)
Daraus folgt
 = a_i)
und damit erhält man die Formel für die kosmologische Rotverschiebung
}{a(t_2)})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17264
|
| TomS Verfasst am: 09. Dez 2014 01:44 Titel: |
|
|
Zusammenfassung
- die Kenntnis der Geometrie sowie der lichtartigen Geodäten ist ausreichend für die Berechnung der Rotverschiebung z
- alle Spezialfälle folgen aus einer universellen Gleichung
- diese Gleichung ist nicht ohne die Vierergeschwindigkeiten formulierbar, d.h. kinematischen und geometrische Effekte sind i.A. nicht trennbar
- kinematische sowie geometrische Effekte können lediglich in Spezialfällen durch Auszeichnung spezieller Beobachter getrennt werden
- die Raumzeitgeometrie ist nur implizit in der Geodäten bzw. der lichtartigen Tangente kodiert
- die universelle Gleichung ist unabhängig von Interpretationen wie "Expansion" o.ä.; sie gilt insbs. auch dann, wenn derartige Interpretationen nicht möglich sind
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 20. Aug 2015 15:57, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17264
|
| TomS Verfasst am: 13. Mai 2015 10:18 Titel: |
|
|
Noch eine Ergänzung zu
}{(u_2,k_2)} )
Formal kann die Geodätengleichung für k
mittels eines sogenannten pfadgeordneten Produktes gelöst werden. Ich verwende als Notation die Umkehrung der oben eingeführten Ableitung D entlang der Geodäten C. Damit folgt der Wellenzahlvektor k an einem beliebigen Punkt auf der Geodäten aus dem Wellenzahlvektor im Startpunkt
^\mu)
Die allgemeingültige Formel für die Rotverschiebung lautet damit
}{(u_2, D^{-1}\,k_1)})
Anstatt den Vektor k entlang der Geodäten C vom Punkt 1 zum Punkt 2 parallelzuverschieben, kann man auch die Geschwindigkeit des Beobachters 2 entgegengesetzt entlang C zum Punkt 1 zurückverschieben. Damit erhält man eine alternative Darstellung
^\mu)
}{(\bar{u},k)})
wobei in dieser letzten Formel ausschließlich Größen vorkommen, die im Punkt 1 definiert sind.
Anschaulich gesprochen wird durch den Paralleltransport ein Beobachter bei 2 durch einen äquivalenten, "imaginären" Beobachter bei 1 ersetzt. Für diesen gilt dann im Punkt formal fast die selbe Formel wir für den rein kinematischen Dopplereffekt in der SRT. Allerdings muss man beachten, dass dennoch gewisse Unterschiede existieren: Eine Geschwindigkeit existiert tatsächlich im Punkt 1, die andere ist mittels Parallelverschiebung entlang der Geodäten C von 2 aus konstruiert; sie enthält die Effekte der Krümmung der Raumzeit entlang C (in den Skalarprodukten in Zähler und Nenner gehen noch die Komponenten des metrischen Tensors ein).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
