| Autor |
Nachricht |
kreis
Anmeldungsdatum: 27.04.2014
Beiträge: 93
|
 kreis Verfasst am: 17. Okt 2014 00:38 Titel: Wie bekomme ich das d\lambda weg? (Wien.Verschiebungsgesetz) |
 |
|
Hi liebe Community, 
ich bin gerade dabei (schon seit`ner weile  ) die letzte Aufgabe meines Experimentalphisikblattes-3 zu lösen und glaube halt, dass meine jetzigen Misserfolge beim bearbieten der Aufgabe einfach nur an meinen geringen Mathematikkentnissen liegen.
Die Aufgabe lautet wie folgt:
Es heißt: "Wienscher Verschiebungsgesetz
Aus der Vorlesung:  \dd \nu = \frac{8 \pi h \nu^3}{c^3}\cdot \frac{1}{exp(\frac{h\nu}{k_BT}) - 1} \cdot \dd \nu ) "
"Man leite hierraus das Wiensche Verschiebungsgesetz ab.
a) Erster Schritt dafür die einfache Umformung von  \longrightarrow \rho(\lambda, T)) .
b) Zweiter Schritt  .
c) Letzter Schritt  Und nach  auflösen.
Meine Überlegungen dazu:
Also ich habe folgende Rechnungen im meinem Heft dazu gemacht, zweifle aber sehr früh schon an einem gewissen Schritt (mit einem *** gekenzeichnet) bei dem ich mir nicht so sicher bin wie ich ein gewisses  wegbekomme. 
Vielleicht sind meine Überlegungen ja sowieso volkommen Falsch  und ich muss nochmal von vorne Anfangen. Hoffe aber ein Experte ist hier unter uns und kann mir dabei helfen den Fehler zu endecken und zu beheben. 
a)
 \dd \nu = \frac{8 \pi h \nu^3}{c^3}\cdot \frac{1}{exp(\frac{h\nu}{k_BT}) - 1} \cdot \dd \nu)
also da
  
und - [Zitat Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles Second Edition ISBN.:978-0-471-873730 Seite 18] -
" The quantity ) is defined from the equality  \dd \lambda = - \rho_T(\nu) \dd \nu ) . The minus sign indicates that, though and ) are both positive, and  have opposite signs. (An increase in frequency gives rise to a corresponding decrease in wavelength."
so dass : \dd \lambda = \frac{8 \pi h (\frac{c}{\lambda})^3}{c^3}\cdot \frac{1}{exp(\frac{h\frac{c}{\lambda}}{k_BT}) - 1} \cdot \frac{c}{\lambda^2}\cdot \dd \lambda = \frac{8 \pi h c}{\lambda^5}\cdot \frac{1}{exp(\frac{hc}{k_BT\lambda}) - 1} \cdot \dd \lambda)
und durch ***division auf beiden Seiten von folgt: = \frac{8 \pi h c}{\lambda^5}\cdot \frac{1}{exp(\frac{hc}{k_BT\lambda}) - 1})
b)
Da -1})= \frac{(y)exp(\frac{y}{x})}{(x^2)(exp(\frac{y}{x}) - 1)^2}) und "Produktregel"
}{\partial \lambda}= \frac{-5\cdot 8 \pi hc}{\lambda^6} \cdot \frac{1}{(exp(\frac{hc}{k_BT \lambda})-1)} + \frac{8 \pi hc}{\lambda^5} \cdot \frac{(\frac{hc}{k_BT})\cdot (exp(\frac{hc}{k_BT \lambda}))}{\lambda^2 \cdot (exp(\frac{hc}{k_BT \lambda})-1)^2} )
}{\partial \lambda}= \frac{8 \pi hc}{\lambda^6(exp(\frac{hc}{k_BT \lambda})-1)} \cdot (\frac{hc \cdot exp(\frac{hc}{k_BT \lambda})}{\lambda (exp(\frac{hc}{k_BT \lambda})-1)} - 5) )
c)
}{\partial \lambda}\stackrel{!}{=} 0 )
da der erste Term nicht null werden kann weil lambda im Nenner steht folgt
}{\lambda (exp(\frac{hc}{k_BT \lambda})-1)} - 5 = 0)
Aus Schreibfaulheit definieren wir 
Das heißt: 
=x \cdot e^x \Leftrightarrow 5e^x - 5 = x \cdot e^x)
e^x +5 =0) ????? Hat zwar eine Lösung weil ich den Graph geplottet habe (siehe Anhang) aber ich finde keine Umkehrfunktion um das hier analytisch zu lösen. Numerisch kann ich das auch nicht so ganz lösen weil ich Numerik noch nicht gehört habe. Darum habe ich mir überlegt die Exponentialfunktion bis auf 3 Terme linear mit einem Taylor-Polynom zu nähern...
(1+x+\frac{x^2}{2!}... \sigma(x^3)) +5 =0)
(1+x+\frac{x^2}{2}) +5 \approx 0)
 und  ..."p-q-Formel"
 = -\frac{7}{2}\pm \sqrt(\frac{49}{4}-\frac{48}{4}) =-\frac{7}{2}\pm \sqrt(\frac{1}{4})= -\frac{7}{2}\pm \frac{1}{2})
 und 
Jetzt könnte man das x zurücksubstituieren und dan für"  " auflösen...
z.B. für x=-3 
Das macht aber nicht so viel Sinn (siehe Graph), weshalb ich für jegliche Verbessurungvorschläge/Korrekturen offen bin.... 
PD: Danke für Diejenige/Derjenige die/der sich das hier durchgelesen hatt.
| Beschreibung: |
|
Download |
| Dateiname: |
Plott.jpg |
| Dateigröße: |
57.6 KB |
| Heruntergeladen: |
433 mal |
Zuletzt bearbeitet von kreis am 17. Okt 2014 11:34, insgesamt 2-mal bearbeitet |
|
 |
asassaaas
Gast
|
| asassaaas Verfasst am: 17. Okt 2014 09:16 Titel: |
|
|
a) Du kannst rho einfach durch Vergleich beider Seiten ablesen, ohne sich Gedanken um Lambda zu machen.
c) Das kannst du mit der Lambertschen W Funktion umformen. Das führt aber immernoch zur Numerik bzw Reihensummation. Ansonsten das Newton-Verfahren verwenden, welches du kennen sollst, da es zum Schulstoff gehört.
|
|
|
Ood
Anmeldungsdatum: 03.01.2014
Beiträge: 80
|
| Ood Verfasst am: 17. Okt 2014 09:43 Titel: |
|
|
| asassaaas hat Folgendes geschrieben: | | Das führt aber immernoch zur Numerik bzw Reihensummation. Ansonsten das Newton-Verfahren verwenden, welches du kennen sollst, da es zum Schulstoff gehört. |
Davon kann man heute leider nicht mehr ausgehen. Zumindest in Baden-Württemberg gehört das Newton-Verfahren nicht mehr zum Pflichtstoff.
|
|
|
kreis
Anmeldungsdatum: 27.04.2014
Beiträge: 93
|
| kreis Verfasst am: 17. Okt 2014 10:26 Titel: |
|
|
a)
| asassaaas hat Folgendes geschrieben: | a) Du kannst rho einfach durch Vergleich beider Seiten ablesen, ohne sich Gedanken um Lambda zu machen.
|
Heißt das etwa dass ich die Aufgabe richtig gelöst habe?
b)
Wenn ich a) richtig gemacht habe sollte b) auch richtig sein.
c)
| asassaaas hat Folgendes geschrieben: | | Das kannst du mit der Lambertschen W Funktion umformen. Das führt aber immernoch zur Numerik bzw Reihensummation. Ansonsten das Newton-Verfahren verwenden, welches du kennen sollst, da es zum Schulstoff gehört. |
Meinst du das hier?
.... Was ist eine Lambertschen W Funktion? (habe ich schon gelegentlich bei der Nutzung von Wolframalpha Mathematica gesehen...)
Geht das denn gar nicht mit Taylor? Also muss ich das mit dem Newton Verfahren machen?
PD: Wir wollen ja irgendwie auf das WIENSCHE VERSCHIEBUNGSGESETZ kommen.... http://de.wikipedia.org/wiki/Wiensches_Verschiebungsgesetz
|
|
|
kreis
Anmeldungsdatum: 27.04.2014
Beiträge: 93
|
|
|
kreis
Anmeldungsdatum: 27.04.2014
Beiträge: 93
|
| kreis Verfasst am: 17. Okt 2014 11:29 Titel: |
|
|
GELÖST!!!! Ok nach einigen Berechnungen ist mir aufgefallen das meine Näherung doch ganz ok ist....
Laut WIKIPEDIA besagt das Wiensche Verschiebungsgesetz :
| Zitat: | Die gebräuchlichste Formulierung des Verschiebungsgesetzes lautet:
: Wellenlänge, bei der die Intensität pro Wellenlängenintervall maximal ist
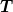 : absolute Temperatur der strahlenden Fläche
Die Frequenz von Wellen dieser Wellenlänge \lambda_\mathrm{max} ist nicht die Frequenz \nu_\mathrm{max}, bei der die Intensität pro Frequenzintervall maximal ist. Zwei weitere Maximumstellen ergeben sich, wenn man statt der Intensität die Photonenrate betrachtet. Es gibt kein „objektives“ Maximum.
(...) Die numerische Lösung ergibt x=4.9651142317.... |
Für meinen Wert von  ergibt sich:
JETZT STELLT SICH NUR NOCH DIE FRAGE FÜR WAS DAS GROSSE K IN DIESEM AUSDRUCK STEHT... WEIß DAS ZUFÄLLIGERWEISE JEMAND?
DANKE!!! 
Zuletzt bearbeitet von kreis am 17. Okt 2014 11:52, insgesamt einmal bearbeitet |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 17. Okt 2014 11:51 Titel: |
|
|
| kreis hat Folgendes geschrieben: |
JETZT STELLT SICH NUR NOCH DIE FRAGE FÜR WAS DAS GROSSE K IN DIESEM AUSDRUCK STEHT... WEIß DAS ZUFÄLLIGERWEISE JEMAND?
|
Kelvin.
|
|
|
kreis
Anmeldungsdatum: 27.04.2014
Beiträge: 93
|
| kreis Verfasst am: 17. Okt 2014 11:57 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | kreis hat Folgendes geschrieben: |
JETZT STELLT SICH NUR NOCH DIE FRAGE FÜR WAS DAS GROSSE K IN DIESEM AUSDRUCK STEHT... WEIß DAS ZUFÄLLIGERWEISE JEMAND?
|
Kelvin. |
´
Ach ja... die Boltzmann-konstante hat ja als Einheit J/K... auserdem muss sich die Einheit der Temperatur im Nenner wegheben damit die Dimension "Länge" für die Wellenlänge rauskommt.... ich Tollpatsch xD
MERCIE!
|
|
|
|
Registrieren
Login
FAQ
Suchen
