| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 30. März 2014 13:04 Titel: FAQ - virtuelle Teilchen und Hawkingstrahlung TomS Verfasst am: 30. März 2014 13:04 Titel: FAQ - virtuelle Teilchen und Hawkingstrahlung |
 |
|
Auch wenn selbst Hawking das Bild "virtueller Teilchen" benutzt, um die nach ihm benannte Hawkingstrahlung zu erklären, ist es eigtl. nicht ganz korrekt.
Im Kontext der Hawkingstrahlung handelt es sich gerade nicht um die aus der Störungstheorie (Feynmandiagramme) bekannten virtuellen Teilchen, sondern um die Problematik, überhaupt teilchenartige Zustände definieren zu können. Aufgrund der nicht-trivialen Raumzeitgeometrie (Existenz eines Horizontes) existiert keine global und eindeutig gültige Definition eines Vakuumzustandes und somit auch keine global gültige Definition von "Teilchen" als Anregung auf demselben. Das ist aber eine Aussage, die unabhängig von der Störungstheorie und der dort verwendeten virtuellen Teilchen formuliert werden kann. Noch besser sieht man dies anhand des Unruh-Effektes, bei dem ein beschleunigter Beobachter im (bzgl. eines ruhenden Beobachters definierten) Vakuum eine thermische Strahlung wahrnimmt.
Die im Kontext der Störungstheorie verwenden virtuellen Teilchen resultieren aus Wechselwirkungsprozessen. Von einem Vertex in einem Feynmandiagramm können äußere oder innere Linien ausgehen; letztere enden an einem anderen Vertex und entsprechen virtuellen Teilchen. Jeder Vertex entspricht einen „Wechselwirkungspunkt“. Im Kontext der Hawkingstrahlung werden jedoch freie, nicht wechselwirkende Felder betrachtet; diese haben offensichtlich nichts mit denen zuvor diskutierten, wechselwirkenden virtuellen Teilchen zu tun.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 30. März 2014 13:25, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Jan 2015 00:02 Titel: TomS Verfasst am: 25. Jan 2015 00:02 Titel: |
 |
|
Nun habe ich argumentiert, dass der Effekt der Hawkingstrahlung nicht auf sogenannte virtuelle Teilchen im herkömmlichen Sinn zurückgeht. Worauf denn dann?
******
Ich möchte dazu im Folgenden eine kurze Zusammenfassung der von Hawking ursprünglich durchgeführten Berechnung der thermischen Strahlung von Schwarzen Löchern präsentieren.
http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.cmp/1103899181
Wie bereits erwähnt - und wie von Hawking bereits in der Einleitung diskutiert - sollte die bekannte Interpretation mittels virtueller Teilchen sowie Tunneleffekt nicht zu wörtlich genommen werden. Hawking's Rechnung kommt ohne einen Tunneleffekt aus, obwohl es inzwischen neuere, alternative Herleitungen gibt, die den Tunneleffekt bemühen (*), und Hawking's Rechnung verwendet keine virtuellen Teilchen.
Zur Erinnerung: virtuelle Teilchen sind ein mathematisches Hilfsmittel, komplizierte Wechselwirkungen näherungsweise störungstheoretisch zu berechnen. Virtuelle Teilchen treten dabei als "innere Linien" in Feynman-Diagrammen auf, die frei zwischen Wechselwirkungspunkten propagieren und über deren Effekte integriert wird. Bei Hawking's Berechnung werden jedoch ausschließlich freie Teilchen ohne jegliche Wechselwirkung verwendet. Der berechnete Effekt ist also nicht störungstheoretischer Natur und existiert auch für wechselwirkungsfreie Felder (mit Ausnahme der Wechselwirkung mit der Raumzeit-Geometrie). Insofern halte ich den Begriff der virtuellen Teilchen in diesem Kontext für irreführend; die mathematischen Objekte haben nichts mit den virtuellen Teilchen der Störungstheorie gemein.
Ich halte mich im folgenden eng an Hawking's mathematische Herleitung. Die wesentliche Idee besteht in einer nicht-mathematischen Erklärung der quantenfeldtheoretischen Konzepte, jedoch ohne Rückgriff auf nicht-definierte Begriffe.
Hawking beginnt mit einer kurzen Einführung zur kanonische Quantisierung freier Felder auf Basis der Fourierzerlegung. Die dabei auftretenden Fourierkoeffizienten entsprechen den Erzeugungs- und Vernichtungsoperatoren. Hawking bemerkt, dass diese Konzepte nicht ohne Weiteres für gekrümmte Raumzeiten übernommen werden können, da sie auf nicht-lokalen Eigenschaften von Feldern beruhen. Insbs. funktioniert die Klassifizierung nach positiven und negativen Frequenzen der Fourierzerlegung nicht global, da diese sowohl von der lokalen Geometrie als auch vom jeweiligen lokalen Beobachter abhängen und somit kein invariante Klassifizierung möglich ist. Eine Schwingungsmode, die bzgl. einer kleinen Umgebung im Raum und einer dort lokalen Zeitkoordinate mit positiver Frequenz erscheint, kann bzgl. einer anderen Umgebung im Raum und bzgl. eines anderen Beobachters mit negativer Frequenz erscheinen u.u. Wesentlich ist außerdem, dass die betrachteten Eigenschwingungen einer allgemein-kovarianten Wellengleichung unter Berücksichtigung der Raumzeitgeometrie genügen. Diese werden für asymptotisch flache Raumzeiten in ebene Wellen übergehen, jedoch im Bereich nicht-trivialer Geometrie (Krümmung, Horizonte) von diesen abweichen. Hawking verwendet für die Quantisierung demnach eine Verallgemeinerung der Fourierzerlegung der Feldoperatoren nach diesen nicht-trivialen Lösungen der Feldgleichung.
Einen Vakuumzustand bzgl. eines bestimmten Satzes von Eigenschwingungen wird definiert als Zustand, in dem keine Schwingungen (= Teilchen) zu diesem Satz von Eigenschwingungen vorhanden sind; die quantenfeldtheoretische Methode zur "Abzählung" dieser Schwingungsmoden liefert Null. Der Vakuumzstand ist demnach abhängig vom zugrundeliegenden Satz von Eigenschwingungen. (Anmerkung: dies ist auch im Rahmen der QFT auf flachen Raumzeiten möglich; dort existiert jedoch eine globale Klassifizierung; und Lorentztransformationen ändern zwar die Frequenzen einer Mode, sie überführen jedoch keine Moden positiver Frequenz in solche negativer Frequenz u.u.).
Hawking argumentiert, dass im wesentlichen die nicht-verschwindende Krümmung für eine Unschärfe in der "lokalen Teilchenzahl" verantwortlich ist, was in gewisser Weise als "Teilchenerzeugung" interpretierbar ist. Obwohl dieser Effekt insbs. für kleine Krümmungen lokal vernachlässigbar ist, folgt global eine makroskopisch sichtbare, thermische Strahlung.
Hawking betrachtet den einfachsten Fall eines masselosen Skalarfeldes auf der gekrümmten Raumzeit einer sphärisch symmetrisch kollabierenden Massenverteilung, aus der ein schwarzes Loch resultiert. Im Außenraum der Massenverteilung gilt dabei trotz Kollaps immer eine stationäre Schwarzschildlösung (deren Gültigkeitsbereich im Zuge des Kollaps nach innen wächst, bis die Materie vollständig in ihren eigenen Schwarzschildradius hinein kollabiert ist). Hawking betrachtet die Lösungen der Wellengleichung des Skalarfeldes und konstruiert daraus die Feldoperatoren.
Dabei legt er diese zunächst in der unendlich fernen, lichtartige Vergangenheit masseloser Felder so fest, dass sie dort ausschließlich positive Frequenzen enthalten. Analog geht er bzgl. vom Ereignishorizont auslaufender Felder sowie in der unendlich fernen, lichtartige Zukunft vor. Daraus resultieren zwei unterschiedliche Darstellungen der Feldoperatoren. Diese werden konstruiert mittels Erzeugungs- und Vernichtungsoperatoren bzgl.
1) aus der lichtartigen Vergangenheit einlaufender Teilchen.
2) in die lichtartige Zukunft auslaufender Teilchen.
Die Darstellung (2) kann mittels geeigneter Linearkombinationen der Operatoren aus (1) gewonnen werden.
Hawking fixiert nun einen Vakuumzustand in der lichtartigen Vergangenheit, d.h. er legt fest, dass dieser Zustand bzgl. (1) keine Teilchen enthalten soll. Anschließend berechnet er den Erwartungswert, dass bzgl. (2) eine nicht-verschwindende Anzahl an Teilchen in der lichtartigen Zukunft vorhanden ist. Die o.g. Linearkombinationen müssen dabei interessanterweise nur für die asymptotisch flache Vergangenheit bzw. Zukunft berechnet werden, d.h. die Details der Lösungen der Wellengleichung in der Nähe des Schwarzen Lochs bzw. für den Kollaps sind nicht notwendig.
Hawking führt clevere, geometrische Argument an, um die Mischungskoeffizienten der Linearkombinationen zu berechnen. Dazu betreibt er im wesentlichen Streutheorie, insbs. eine Art distorted-wave Approximation für die o.g. Feldoperatoren auf der nicht-trivialen Raumzeitgeometrie. Die Details kann ich hier nicht ausführen.
Letztlich folgt, dass ausgehend von dem Vakuumzustand in der unendlich fernen, lichtartigen Vergangenheit ein positiver, exakt thermischer Fluss an masselosen Spin-0 Teilchen in der unendlich fernen, lichtartigen Zukunft resultiert. Dies resultiert aus unterschiedlichen (quantenmechanischen) Absorptions- und Emissionskoeffizienten des schwarzen Lochs. D.h. man erhält eine Strahlung entsprechend der Bose-Einstein-Statistik. Hawking argumentiert außerdem, dass für Spin-1 Teilchen ein analoges Resultat folgt, und dass für Fermionen stattdessen die Fermi-Dirac-Statistik gilt. Zuletzt motiviert Hawking, wie die Ergebnisse für massebehaftete Felder zu korrigieren sind. Hier geht in die Frequenz der Strahlungsgesetze die Ruhemasse der betrachteten Teilchen ein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 17. Feb 2015 13:04, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 17. Feb 2015 12:58 Titel: TomS Verfasst am: 17. Feb 2015 12:58 Titel: |
 |
|
Sehr treffend fand ich den Kommentar von Joan Baez:
| Zitat: | ... well, you'll find Hawking radiation explained this way in a lot of pop-science treatments:
"Virtual particle pairs are constantly being created near the horizon of the black hole, as they are everywhere. Normally, they are created as a particle-antiparticle pair and they quickly annihilate each other. But near the horizon of a black hole, it's possible for one to fall in before the annihilation can happen, in which case the other one escapes as Hawking radiation."
In fact this argument also does not correspond in any clear way to the actual computation. Or at least I've never seen how the standard computation can be transmuted into one involving virtual particles sneaking over the horizon, and in the last talk I was at on this it was emphasized that nobody has ever worked out a "local" description of Hawking radiation in terms of stuff like this happening at the horizon. |
Der insgs. sehr lesenswerte Artikel ist hier zu finden:
http://www.physicsfaq.co.uk/Relativity/BlackHoles/hawking.html
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 11. Mai 2015 12:34 Titel: TomS Verfasst am: 11. Mai 2015 12:34 Titel: |
 |
|
Nachdem die Erläuterungen zu Hawkings Originalarbeit im Wikipedia-Artikel http://de.wikipedia.org/wiki/Hawking-Strahlung zum großen Teil von mir stammen, erlaube ich mir mal, sie hier zu kopieren:
Erläuterungen zu Hawkings Originalarbeit
Vorbemerkungen
Seit Hawkings Veröffentlichung
http://www.itp.uni-hannover.de/~giulini/papers/BlackHoleSeminar/Hawking_CMP_1975.pdf
wurde eine Reihe unterschiedlicher Methoden zur Herleitung der thermischen Strahlung Schwarzer Löcher entwickelt, die auf verschiedenen Wegen seine ursprünglichen Ergebnisse bestätigen und ergänzen.
Hawking verwendete aus Gründen der Einfachheit in seiner Originalarbeit ein masseloses Skalarfeld. Die Ergebnisse können jedoch auf andere Teilchen wie beispielsweise Photonen und allgemeiner auch auf masselose Fermionen erweitert werden. Die Hawking-Strahlung enthält prinzipiell auch massebehaftete Teilchen, allerdings ist deren Beitrag im Vergleich zu masselosen Teilchen um viele Größenordnungen unterdrückt.
Entgegen den häufig anzutreffenden Veranschaulichungen verwendete S. Hawking in keine quantenmechanische Störungstheorie, wie der Begriff der „virtuellen Teilchen“ suggerieren könnte. Wäre dies der Fall, so müsste das Endergebnis von der Kopplungskonstante der betrachteten Wechselwirkung, wie z.B. der Feinstrukturkonstante bei der elektromagnetischen Wechselwirkung, abhängen. Das Ergebnis ist jedoch bereits für freie, nicht-wechselwirkende Felder gültig.
Erläuterungen
Hawking arbeitet in einer semiklassischen Näherung, d.h. er betrachtet eine freie Quantenfeldtheorie auf einer klassischen, schwach gekrümmten Raumzeit. Relevant ist im Wesentlichen die globale Struktur der Raumzeit sowie insbesondere die Existenz eines Ereignishorizontes.
Hawking setzt einen sphärisch-symmetrischen Kollaps einer Masse M voraus, d.h. er geht nicht von einer rein statischen Schwarzschild-Metrik aus. Letztere gilt jedoch aufgrund des Birkhoff-Theorems im Außenraum des Kollapses exakt. Die Details der Innenraumlösung sind für die Argumentation irrelevant.
Hawking beginnt mit der kanonischen Quantisierung freier Felder auf Basis einer verallgemeinerten Fourierentwicklung. Diese Fouriermoden sind dabei speziell Lösungen der Klein-Gordon-Gleichung für masselose Skalarfelder auf der Raumzeit-Geometrie. Die dabei notwendige Zerlegung der Fouriermoden nach positiven und negativen Frequenzen sowie die daraus folgende Klassifizierung von Teilchen und Antiteilchen sind aufgrund der Raumzeitgeometrie nicht eindeutig. Im Zuge der Quantisierung kann ein Beobachter mathematisch jeweils für ihn gültige Erzeugungs- und Vernichtungsoperatoren, sowie einen für ihn gültigen Vakuumzustand (Fock-Zustand) definieren, in dem entsprechend seiner Klassifizierung keine Teilchen und Antiteilchen existieren. Während diese Beobachterabhängigkeit in der Minkowski-Raumzeit für die Erzeugungs- und Vernichtungsoperatoren sowie für den Vakuumzustand letztlich irrelevant ist, führt sie bei Anwesenheit eines Ereignishorizontes zu inäquivalenten Vakuumzuständen.
Mathematisch existiert eine Transformation, die sogenannte Bogoljubov-Transformation, die die Erzeugungs- und Vernichtungsoperatoren beider Beobachter ineinander überführt. Hawking fixiert zunächst einen Vakuumzustand sowie die Erzeugungs- und Vernichtungsoperatoren für die ferne Vergangenheit. In diesem Zustand verschwindet der Erwartungswert des Teilchenzahloperators (definiert für die ferne Vergangenheit). Anschließend bestimmt er die Bogoljubov-Transformation für die Erzeugungs- und Vernichtungsoperatoren für die ferne Zukunft. Dazu wird im Wesentlichen die Streuung der Fouriermoden am kollabierenden Schwarzen Loch berechnet. Der für die Hawking-Strahlung relevante Anteil stammt dabei aus der Streuung der Moden innerhalb des kollabierenden Körpers. Damit kann nun der Erwartungswert des Teilchenzahloperators (definiert für die ferne Zukunft) im ursprünglichen Vakuumzustand (definiert für die ferne Vergangenheit) berechnet werden. Es zeigt sich, dass dieser Erwartungswert nicht verschwindet! Der Beobachter in der fernen Zukunft sieht demnach nicht den für ihn gültigen Vakuumzustand, sondern einen Zustand, in dem tatsächlich Teilchen und Antiteilchen (bzgl. seiner Definition) enthalten sind. Die thermische Natur des Spektrums folgt aus der genauen Form der Bogoljubov-Transformation.
Der physikalische Kern von Hawkings Argumentation lautet demnach wie folgt: Der Kollaps sowie die Anwesenheit eines Horizontes führt zu inäquivalenten Vakuumzuständen. Während in einer flachen Raumzeit die Zeitentwicklung das Vakuum invariant lässt, ist dieses in einer Raumzeit mit Schwarzen Loch einem „Streuprozess“ unterworfen ist, der das initiale Vakuum in einen thermischen Zustand überführt.
Mathematische Details
Hawking betrachtet die freie Klein-Gordon-Gleichung

eines masselosen Skalarfeldes.
Er führt auf den lichtartigen Cauchy-Hyperflächen  und und  vollständige Funktionensysteme vollständige Funktionensysteme 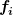 und und 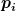 ein, mittels derer er den selben Feldoperator ein, mittels derer er den selben Feldoperator  jeweils als Fouriersumme von Erzeugern und Vernichtern (bzgl. der beiden Funktionensysteme) darstellt: jeweils als Fouriersumme von Erzeugern und Vernichtern (bzgl. der beiden Funktionensysteme) darstellt:

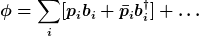
“…” steht dabei für ein weiteres Funktionensystem auf der lichtartigen Cauchy-Hyperfläche des Horizontes. Dieses ist prinzipiell notwendig, um die Cauchy-Daten zu vervollständigen, spielt jedoch im Folgenden keine Rolle.
Hawking definiert zunächst den Vakuumzustand

bezüglich der von  einlaufenden Teilchen. einlaufenden Teilchen.
Der allgemeine Zusammenhang zwischen den beiden Familien von Erzeugern und Vernichtern besteht nun in der Bogoljubov-Transformation


Hawking zeigt im Folgenden, dass die Streuung der aus  einlaufenden Moden am Schwarzen Loch dazu führt, dass ein Beobachter auf einlaufenden Moden am Schwarzen Loch dazu führt, dass ein Beobachter auf  dem Zustand dem Zustand 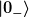 einen nicht-verschwindenden Teilcheninhalt einen nicht-verschwindenden Teilcheninhalt
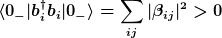
zuschreibt. Die Erzeugungsrate der Teilchen folgt dabei direkt aus den Koeffizienten  der Bogoljubov-Transformation. Diese mischen den Vernichtern auf der Bogoljubov-Transformation. Diese mischen den Vernichtern auf  einen Anteil von Erzeugern auf einen Anteil von Erzeugern auf  bei. bei.
Die Streuung der Moden erfolgt dabei sowohl an der äußeren Schwarzschildgeometrie als auch an der Geometrie des Innenraums des kollabierenden Sterns. Letztere ergibt einen nicht-trivialen Beitrag zu den 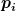 -Moden, die dann die spezielle Form der Bogoljubov-Koeffizienten bewirken. -Moden, die dann die spezielle Form der Bogoljubov-Koeffizienten bewirken.
Der Beitrag einer Mode mit Radialfrequenz 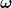 ist dabei ist dabei
 \sim \frac{1}{e^{2\pi\omega/\kappa} -1})
mit  . D.h. es liegt thermische Strahlung mit Temperatur . D.h. es liegt thermische Strahlung mit Temperatur

(in natürlichen Einheiten) entsprechend der Bose-Einstein-Statistik vor.
Hawking erläutert grob, dass für Fermionen ein Verlauf
 \sim \frac{1}{e^{2\pi\omega/\kappa} +1})
entsprechend der Fermi-Dirac-Statistik zu erwarten ist.
Der Beitrag massebehafteter Teilchen ist exponentiell unterdrückt, da in diesem Fall in der Frequenz bzw. der entsprechenden Energie die Ruhemasse m entsprechend

 \sim \frac{1}{e^{2\pi m /\kappa} })
zu berücksichtigen ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















