| Autor |
Nachricht |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 11:58 Titel: Hohlkugel mit Punktladung - Nicht konzentrisch JohnLemon Verfasst am: 28. März 2014 11:58 Titel: Hohlkugel mit Punktladung - Nicht konzentrisch |
 |
|
Hallo 
Ich hätte ne kleine Frage an euch, bin erst im 2. Semester und wir haben erst mit elektrostatik begonnen, also wird die Antwort hier nicht extrem sein (habe gegoogelt und was mit spiegelladungen usw. gefunden, aber auf soetwas sollte das NICHT hinauslaufen  ) )
(Vielleicht übersehe ich nur den leichtesten Weg, aber ich Hänge momentan)
Aufgabe:
Gegeben sei eine Hohlkugel aus leitendem Material mit einem Radius R. Darin sei eine Punktladung (-9 MikroC) an einem Punkt im Abstand R/2 von der Mitte der Hohlkugel angebracht. Die Schale der Hohlkugel sei elektrisch neutral.
A) Auf der inneren Oberfläche der Hohlkugel werden welche Ladungen induziert? sind die inhomogen oder homogen verteilt?
Ich denke mal positiv und inhomogen. Positiv weil die Ladung im Inneren negativ ist, somit durch Influenz negative Ladungen an der Oberfläche induziert. Inhomogen, da die Ladung nicht im Mittelpunkt ist, und eine inhomogene Verteilung notwendig ist damit das Feld im Inneren = 0 ist. (Durch die Punktladung kann ich die Innenseite quasi wie eine geladene Hohlkugel betrachten?  ) )
B) Auf der äußeren Oberfläche werden welche Ladungen induziert? Inhomogen oder homogen?
Negativ und homogen. Negativ weil die Positiven durch die Influenz ja eher auf der Innenseite sind. Da Innenseite mit Punktladung jetzt zusammen "feldfrei" (  ) sind verteilen diese sich homogen (naja kann man das so begründen, ist das überhaupt ansatzweise richtig? hab es mal gegoogelt und alle streitn sich darüber mit formeln weit über meinem derzeitigen Wissen, wobei die meisten sagen es ist homogen außen ^^) ) sind verteilen diese sich homogen (naja kann man das so begründen, ist das überhaupt ansatzweise richtig? hab es mal gegoogelt und alle streitn sich darüber mit formeln weit über meinem derzeitigen Wissen, wobei die meisten sagen es ist homogen außen ^^)
C) welchen Verlauf zeigt das elektrische Feld außerhalb der Hohlkugel?
Wenn meine Begründung stimmt müsste dass wie die einer (negativ) geladenen Hohlkugel sein (obwohl die Schale neutral ist, aber die negative Ladung am äußeren Rand erzeugt dieses Feld, da Punktladung und positive auf innerer Seite sich aufheben.
D) welchen Verlauf zeigt das elektrische Feld innerhalb der Hohlkugel?
Sollte ja feldfrei sein..
Tut mir leid wenn ich Schwachsinn schreibe 
Danke an alle die helfen! 
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 28. März 2014 13:04 Titel: GvC Verfasst am: 28. März 2014 13:04 Titel: |
 |
|
| JohnLemon hat Folgendes geschrieben: | | B) Auf der äußeren Oberfläche werden welche Ladungen induziert? Inhomogen oder homogen? |
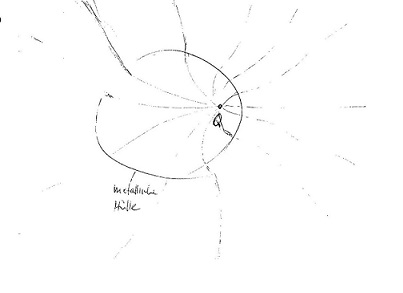
Ich denke ja, dass die negative Ladung auf der Außenseite der metallischen Kugel genauso inhomogen verteilt ist wie auf der Innenseite, denn innerhalb der metallischen Kugelschale ist das Feld Null. Dass kann aber nur sein, wenn den inhomogen verteilten positiven Ladungen auf der Innenseite entsprechend inhomogen verteilte negative Ladungen auf der Außenseite gegenüber stehen. Die Feldstärke in der Schale ergibt sich dann aus der Überlagerung des (verzerrten) Feldes der Punktladung und des "induzierten" Feld innerhalb der Schale. Die Feldlinien müssen jedenfalls immer senkrecht auf der Oberfläche der Kugelschale stehen, sowohl innen wie außen.
Ich gehöre mit meiner Meinung somit zu der Minderheit derjenigen, die vor knapp einem Jahr dieses Phänomen hier (oder in einem anderen Forum) bereits einmal diskutiert haben.
Meiner Meinung nach sieht der Feldverlauf insgesamt in etwa so aus:
| Beschreibung: |
|
| Dateigröße: |
12.88 KB |
| Angeschaut: |
10232 mal |
|
|
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 13:10 Titel: JohnLemon Verfasst am: 28. März 2014 13:10 Titel: |
 |
|
|
Ja, mir erscheint als hätten beide Seiten logische Argumente. Kann man es nicht so sehen, dass die innere Feldstärke nicht schon aufgrund der Zusammenwirkung von positiver Innenseite und Punktladung gleich 0 ist an dieser Stelle (ohne die Außenseite miteinzubeziehen) und deshalb die Außenseite homogen ist?
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 28. März 2014 13:41 Titel: as_string Verfasst am: 28. März 2014 13:41 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Dass kann aber nur sein, wenn den inhomogen verteilten positiven Ladungen auf der Innenseite entsprechend inhomogen verteilte negative Ladungen auf der Außenseite gegenüber stehen. |
Nö, da ist ja noch die negative Ladung im Inneren, die ja gerade durch die inhomogene Ladung auf der Innenseite erst "abgeschirmt" wird.
Wir sind uns doch einig, dass das Potential an der Innenseite schon an jeder Stelle gleich sein muss. Warum sollte es dann von außen gesehen eine Rolle spielen, wo die Ladung im Innern sich genau befindet?
Man "sieht" Ladungen nicht durch einen Leiter hindurch!
Du kompensierst mit der positiven Ladung an der Innenseite die negative Punktladung und auch umgekehrt!. Warum solltest Du dann die positive Ladung an der Innenseite nochmal durch entsprechend verteilte negative Ladung an der Außenseite kompensieren wollen?
Gruß
Marco
|
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 15:53 Titel: JohnLemon Verfasst am: 28. März 2014 15:53 Titel: |
 |
|
|
Hab mal gefragt und angeblich soll das Feld im inneren nicht 0 sein, wie ist es dann?
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 19:25 Titel: JohnLemon Verfasst am: 28. März 2014 19:25 Titel: |
 |
|
|
ja aber so ein trick mit einer gespiegelten Ladung funktioniert nur für das innere Feld, außen wäre es schon radialsymmetrisch oder?
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 28. März 2014 19:40 Titel: D2 Verfasst am: 28. März 2014 19:40 Titel: |
 |
|
Ja, wobei die Mitte die Punktladung selbst bildet + elektrisches Feld steht senkrecht zu der leitenden Hohlkugel.
Hier haben wir dies mal diskutiert
http://www.physikerboard.de/htopic,33439,feld++rohr.html
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 20:20 Titel: JohnLemon Verfasst am: 28. März 2014 20:20 Titel: |
 |
|
Gut ich würde es jetzt so beantworten:
Die von der Punktladung induzierten positiven Ladungen auf der innenseite sind inhomogen verteilt, da die Punktladung die protonen auf einer Seite stärker anzieht (bzw elektronen abstoßen). Zwischen innenseite und punktladung gibt es aber sehrwohl ein Feld, z.B ermittelbar mit einer Spiegelladung. Die Innenschicht und die negative Punktladung sind gemeinsam aber nach außen hin neutral(somit auch kein Feld welches Einfluss auf die äußere Schicht hat- Satz von Gauß)
Somit gibt es keinen Grund warum die Außenseite auch inhomogen verteilt sein sollte, da der rest ja bereits neutral ist.
Damit ist die äußere Fläche quasi wie eine geladene Hohlkugel zu behandeln mit einem radialsymmetrischen Feld nach außen. (wobei die linien natürlich hin zur oberfläche zeigen weil diese ja negativ geladen ist)
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 28. März 2014 20:44 Titel: D2 Verfasst am: 28. März 2014 20:44 Titel: |
 |
|
Versuche es bitte noch mal-
_________________
Lösungen gibt es immer, man muss nur darauf kommen.
Zuletzt bearbeitet von D2 am 28. März 2014 22:31, insgesamt einmal bearbeitet |
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 22:23 Titel: JohnLemon Verfasst am: 28. März 2014 22:23 Titel: |
 |
|
hm naja das innere Feld ist mir schon irgendwie klar, wobei ich nicht weiß wie genau man mit spiegelladungen umgeht da wir sie nicht gemacht haben. Nur versteh ich nicht ganz warum außen gar kein Feld ist.
Ich meine ich könnte es wie einen Faradayschen Käfig sehen, nur halt umgedreht, dass es nach außen abschirmt. Es kommt aufgrund der Kraftwirkung F=QE auf die in der Hülle frei beweglichen Ladungen Q zu räumlichen Umverteilung der Ladungen an der Oberfläche bis die tangential auf der Oberfläche stehende elektrische Feldkomponente (der Innenseite) null wird und damit ein Ausgleich gefunden ist. Dadurch entspringt bzw. endet im statischen Fall der elektrische Fluss an der Oberfläche der Hülle, womit dann das äußere Feldfrei bleibt.
Hm ja, mich würde nur interessiern welche Rolle die negativen Ladungen am Außenrand dann spielen? Aber vielleicht sollte ich mir einfach einen Faradayschen Käfig genauer ansehen...
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 28. März 2014 22:29 Titel: D2 Verfasst am: 28. März 2014 22:29 Titel: |
 |
|
Das Feld außen muss du selbst zeichnen(fehlt noch), dann werden wir sehen was du verstanden hast.
| Beschreibung: |
|
| Dateigröße: |
7.57 KB |
| Angeschaut: |
10036 mal |

|
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 28. März 2014 22:51 Titel: JohnLemon Verfasst am: 28. März 2014 22:51 Titel: |
 |
|
Ja da schwanke ich eben noch:
1)Wenn es wirklich wie ein Faradayscher Käfig funktioniert müsste das Feld außen =0 sein.
2)Eher glaube ich aber dass das Gesamtsystem nach außen hin ja schlussendlich negativ geladen ist und somit das Feld außen jenes einer geladenen Hohlkugel. Somit wäre das Außenfeld gleich dem Feld einer (virtuellen) Punktladung im Mittelpunkt der Kugel.
Das wäre mein Vorschlag, wenn er falsch ist dann würde ich gerne wissen wo ca. der Fehler ist (Wie gesagt wir haben erst gerade mit Elektrostatik begonnen)
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 29. März 2014 09:04 Titel: D2 Verfasst am: 29. März 2014 09:04 Titel: |
 |
|
Mein Vorschlag ist, alle dir gegebene Links (so viel waren es nicht) und die
Texte dazu aufmerksam durchzulesen. Ich habe so ein Gefühl, dass
du dies noch nicht wirklich getan hast. Zeichnen doch die elektrische Linien
so wie du kannst, dann wird bestimmt einer oder anderer sich melden.
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 29. März 2014 10:31 Titel: JohnLemon Verfasst am: 29. März 2014 10:31 Titel: |
 |
|
Naja, gilt der gaußsche Satz nur wenn die Punktladung in der Mitte ist.
In deinem Thread habe ich gelesen:
Der Grund für ungleichmäßige Feldverteilung liegt in der Tatsache begründet, dass metallische Oberflächen Äquipotentialflächen sind und deshalb keine Tangentialfeldstärken zulassen. So bewirkt die Influenz eine Ladungsverschiebung dergestalt, dass die Tangentialfeldstärke verschwindet. Da jede Ladung Quelle eines elektrischen Feldes ist, ist eine durch Influenz bewirkte größere oder kleinere Ladungsdichte auch Quelle eines größeren oder kleineren elektrischen Feldes.
Trotzdem macht das doch das einzeichnen des äußeren Feldes extrem kompliziert.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 10:57 Titel: as_string Verfasst am: 29. März 2014 10:57 Titel: |
 |
|
Hallo,
so ganz verstehe ich nicht, was noch offen ist. Du hast ja schon geschrieben, dass das Außenfeld genau so aussieht, wie wenn Du eine geladene, leitende Kugel hast, oder auch, wie wenn Du eine Punktladung in der Mitte der Hohlkugel hast und sonst nichts.
Gruß
Marco
|
|
 |
JohnLemon

Anmeldungsdatum: 02.03.2014
Beiträge: 31
|
 JohnLemon Verfasst am: 29. März 2014 11:04 Titel: JohnLemon Verfasst am: 29. März 2014 11:04 Titel: |
 |
|
|
ja Marco, der Meinung bin ich ja auch, und für mich wäre das auch gelöst, aber anscheinend hat D2 eine andere Ansicht und mich würde interessiern was er meint.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 11:11 Titel: as_string Verfasst am: 29. März 2014 11:11 Titel: |
 |
|
Ja, das wäre nicht das erste Mal...
Im Prinzip hast Du schon alles gesagt dazu, denke ich. Die Kugeloberfläche ist eine Äquipotentialfläche. Egal, wie das Feld innen aussieht (zumindest solange statisch), das Feld im Äußeren ist dann immer das selbe, und weil die Äquipontentialfläche kugelsymmetrisch ist, muss auch das Außenfeld kugelsymmetrisch sein. Wie das Feld genau aussieht bekommst Du dann genau so über Gauß mit der Summe der eingeschlossenen Ladungen und so, wie Du das auch schon erwähnt hast.
Vielleicht noch eine Bemerkung zu Gauß: Natürlich ist der immer gültig, ist ja ein mathematischer Satz... Aber nicht immer kann man ihn gewinnbringend einsetzen. Einfach ist es z. B. hier, wenn man eine Kugelsymmetrie verwenden kann, dann weiß man, dass auf den Flächen aller konzentrischen Kugeln die selbe Feldstärke senkrecht auf der Fläche steht und kann dann recht einfach weiter rechnen. Im Allgemeinen ist das natürlich nicht so einfach...
Gruß
Marco
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. März 2014 11:42 Titel: Huggy Verfasst am: 29. März 2014 11:42 Titel: |
 |
|
Man muss bei diesem Problem unterscheiden, ob man eine "geerdete" Hohlkugel oder eine isolierte Hohlkugel betrachtet. Geerdet bedeutet dabei, das die Hohlkugel dasselbe Potential haben soll, wie ein Punkt im Unendlichen. Man kann sich das so vorstellen, dass die Hohlkugel mit einem weit entfernten Ladungsreservoir durch einen feinen leitenden Draht verbunden ist, über den Ladungen beliebigen Vorzeichens fließen können, um die Potentialgleichheit herzustellen.
Geerdete Hohlkugel
Das Feld im Inneren der Hohlkugel kann mit der Methode der Spiegelladung bestimmt werden. Die auf der Hohlkugel influenzierte Ladungsverteilung kann aus der Richtungsableitung des Innenfeldes auf dem Rand der Hohlkugel in der Richtung senkrecht zur Oberfläche der Hohlkugel bestimmt werden. Die influenzierte Ladungsverteilung ist natürlich inhomogen. Die gesamte influenzierte Ladung ist gleich der Spiegelladung q'.
Das Feld im Außenbereich der Hohlkugel ergibt sich allerdings nicht aus der Überlagerung der Felder der Punktladung und ihrer Spiegelladung, wie es in dem von D2 verlinkten Bild angedeutet ist. Die Spiegelladung ist ja nicht wirklich vorhanden. Es kann nach dem Gaußschen Gesetz auch nicht Null sein, da die Spiegelladung nicht betragsmäßig gleich der gegebenen Punktlaung ist. Man muss es wohl durch numerische Integration des Feldes der influenzierten Ladungsverteilung im Außenbereich bestimmen und dazu das Feld der gegebenen Punktladung addieren.
Isolierte Kugel
Dieser Fall kann aus dem vorigen hergeleitet werden. Man betrachtet zunächst die geerdete Kugel und unterbricht dann die Leitung zu dem Ladungsreservoir. Jetzt bringt man eine zusätzliche Ladung -q' auf die Hohlkugel. Dadurch wird deren Gesamtladung Null, wie es eine isolierte Kugel erfordert. Da die Hohlkugel eine Äquipotentialfläche ist, verteilt sich diese zusätzliche Ladung gleichmäßig auf der Hohlkugel. Das Feld im Innenbereich ändert sich dadurch nicht, weil eine gleichmäßige Ladungsverteilung auf einer Kugelschale in deren Inneren kein Feld erzeugt. Im Außenbereich der Kugelschale erzeugt sie das gleiche Feld, wie eine Punktladung -q' im Zentrum der Hohlkugel. Dieses ist zu dem vorher betrachteten Feld der geerdeten Kugel zu addieren.
Im Jackson, Classical Electrodynamics, ist das Problem in Kapitel 2 relativ ausführlich behandelt.
In der Aufgabe steht, die Hohlkugel sei elektrisch neutral. Das interpretiere ich als isolierte Holkugel.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 12:01 Titel: as_string Verfasst am: 29. März 2014 12:01 Titel: |
 |
|
Ähm, ja, das ist ja alles schön und gut...
Aber was genau hat das jetzt mit der Aufgabe bzw. dem letztlich übrig gebliebenen Problem zu tun? Hier ist es eine (isoliert) leitende Hohlkugel, in der eine Punktladung ist, die sich nicht im Mittelpunkt der Kugel befindet.
Das Innenfeld bekommt man gut mit der Methode der Spiegelladungen hin. Das einzig fragliche war jetzt das Außenfeld, bzw. ob sich das anders verhalten kann, als das eine Punktladung im Zentrum, durch die Punktladung, die hier nicht im Zentrum ist.
Ich meine nein, GvC hatte was anderes gesagt und D2 anscheinend auch, äußert sich aber nicht so recht, was denn nun...
Gruß
Marco
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. März 2014 12:22 Titel: Huggy Verfasst am: 29. März 2014 12:22 Titel: |
 |
|
| as_string hat Folgendes geschrieben: |
Das einzig fragliche war jetzt das Außenfeld, bzw. ob sich das anders verhalten kann, als das eine Punktladung im Zentrum, durch die Punktladung, die hier nicht im Zentrum ist. |
Darauf bin ich doch eingegangen. Das Feld im Außenbereich bei isolierter Kugel ergibt sich als Summe der Felder der gegebenen Punktladung, einer Ladung -q' im Zentrum der Hohlkugel und des Feldes der induzierten Ladungsverteilung bei Annahme einer geerdeten Kugel. Ich sehe keine Grund, weshalb die Summe dieser drei Felder gleich dem Feld einer einzelnen Punktladung sein sollte, wo immer auch postiert.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 12:36 Titel: as_string Verfasst am: 29. März 2014 12:36 Titel: |
 |
|
Na weil ich auf der kompletten Kugelaußenseite eben das selbe Potential habe. 
Ich verstehe Dich glaube ich gerade nicht so richtig... 
Gruß
Marco
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 12:47 Titel: as_string Verfasst am: 29. März 2014 12:47 Titel: |
 |
|
Ok, vielleicht nochmal anders, was ich meine:
Stellt Euch eine Hohlkugel vor, deren Schale aber eine gewisse Dicke hat. Insgesamt soll dieses Leitervolumen neutral geladen sein.
Wenn ich innerhalb des Innenradius (also im Hohlraum in der Kugel) eine beliebige Ladungsverteilung habe, dann werden sich die freien Ladungsträger im Leitervolumen so sortieren, dass innerhalb des Leitervolumens wieder alles feldfrei ist, logisch.
Das bedeutet also, die Innenseite "spiegelt" die innere Ladungsverteilung wider, genau so, dass ein kleines Stück weiter ins Volumen rein gar kein Feld mehr ist.
Da die Ladungsträger, die das an der Innenseite so machen, bei einer isolierten Kugel ja irgendwo herkommen müssen, fehlen die natürlich an der Außenseite. Da aber dort ja erstmal alles feldfrei ist, verteilen diese Ladungsträger (oder "Löcher" quasi, je nach Polung und eigentlich auch völlig egal...) sich völlig gleichmäßig. Warum sollten sie auch eine Vorzugsrichtung haben? Fakt ist: nach Innen ist ja aber der Innenseite alles feldfrei, nach außen ist es dann so, als ob nur diese dünne geladene Hohlkugel vorhanden wäre. Da wir wissen, dass das Außenfeld einer geladenen leitenden Kugel so ist, wie das einer einzelnen Punktladung in der Mitte, ist es da eben auch ganz genau so.
Ich weiß nicht genau, ob wir nur aneinander vorbei reden, aber eigentlich ist das doch alles recht klar, oder?
Gruß
Marco 
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. März 2014 13:14 Titel: Huggy Verfasst am: 29. März 2014 13:14 Titel: |
 |
|
|
Deine Argumentation kann ich nicht nachvollziehen. Du meinst, dass das Außenfeld lediglich durch den Anteil de gleichmäßigen Ladungsverteilung auf der Kugelschale bestimmt wird, der nach der Jacksonherleitung benötigt wird, die isolierte Kugelschale elektrisch neutral zu machen. Nach dieser Vorstellung müsste das Außenfeld der geerdeten Kugelschale Null sein, weil der Anteil der gleichmäßigen Ladungsverteilung dann Null ist. Das ist es aber nach dem Gaußschen Gesetz nicht.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 13:38 Titel: as_string Verfasst am: 29. März 2014 13:38 Titel: |
 |
|
Wieso sollte das Außenfeld dann null sein, wenn ich eine Kugelschale mit gleichmäßiger Ladungsverteilung habe???
Nochmal: Hohlkugel-Innenschale hebt Feld der in ihr vorhandenen beliebigen Ladungsverteilung auf -> Feldfreiheit im Leitervolumen. Die dann fehlende Ladung im Leitervolumen bildet eine gleichmäßige/homogen geladene Kugelschale an der Leiter-Außenseite-> Feld im Leitervolumen wird dadurch unbeeinflusst bleiben, Feld im Außenbereich ist das einer homogen geladenen Kugel gleich einer Punktladung im Zentrum der homogen geladenen Kugel.
Das ist doch eigentlich ziemlich offensichtlich, denke ich, oder?
Gruß
Marco
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. März 2014 14:14 Titel: Huggy Verfasst am: 29. März 2014 14:14 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | Wieso sollte das Außenfeld dann null sein, wenn ich eine Kugelschale mit gleichmäßiger Ladungsverteilung habe??? |
Habe ich nicht behauptet. Bitte diesen Teil bei mir noch mal genau lesen.
| Zitat: | | Das ist doch eigentlich ziemlich offensichtlich, denke ich, oder? |
Für mich ist das überhaupt nicht offensichtlich.
Für das Feld einer Ladungsverteilung gilt das Superpositionsprinzip. Die Felder der einzelnen Teilladungen können unabhängig voneinander bestimmt werden und dann zu dem Gesamtfeld addiert werden. Diese Prinzip gilt auch, wenn sich Leiter in dem Feld befinden. Die Leiter bewirken lediglich, dass sich zusätzlich zu den gegebenen Ladungen noch induzierte Ladungen ergeben, die so beschaffen sein müssen, dass das Gesamtfeld für die Leiterbereiche Äquipotentialflächen ergibt. Sind wir uns bis hier einig?
Insbesondere gibt es kein eigenständiges Abschirmprinzip für geschlossene Leiterflächen. Die Abschirmwirkung (Faradayscher Käfig) ergibt sich automatisch oder auch nicht aus dem Superpositionsprinzip unter Einschluss der Felder der induzierten Ladungen. Das Superpositionsprinzip bewirkt, dass der Innenraum einer geschlossenen Leiterfläche gegen die Felder von Ladungen außerhalb der Fläche abgeschirmt ist. Das Superpositionsprinzip bewirkt aber nicht, dass der Außenraum einer geschlossenen Leiterfläche gegenüber den Feldern von Ladungen im Innenraum abgeschirmt ist. Siehe dazu auch den Wikiartikel zum Faradayschen Käfig. Und das macht deine Argumentation hinfällig.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 14:52 Titel: as_string Verfasst am: 29. März 2014 14:52 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Für das Feld einer Ladungsverteilung gilt das Superpositionsprinzip. Die Felder der einzelnen Teilladungen können unabhängig voneinander bestimmt werden und dann zu dem Gesamtfeld addiert werden. Diese Prinzip gilt auch, wenn sich Leiter in dem Feld befinden. Die Leiter bewirken lediglich, dass sich zusätzlich zu den gegebenen Ladungen noch induzierte Ladungen ergeben, die so beschaffen sein müssen, dass das Gesamtfeld für die Leiterbereiche Äquipotentialflächen ergibt. Sind wir uns bis hier einig? |
Ja, klar.
| Huggy hat Folgendes geschrieben: | | Insbesondere gibt es kein eigenständiges Abschirmprinzip für geschlossene Leiterflächen. |
Ich weiß nicht, was ein "eigenständiges Abschirmprinzip" sein soll.
| Huggy hat Folgendes geschrieben: | | Die Abschirmwirkung (Faradayscher Käfig) ergibt sich automatisch oder auch nicht aus dem Superpositionsprinzip unter Einschluss der Felder der induzierten Ladungen. |
Das ist es ja, was ich geschrieben habe, oder?
| Huggy hat Folgendes geschrieben: | | Das Superpositionsprinzip bewirkt, dass der Innenraum einer geschlossenen Leiterfläche gegen die Felder von Ladungen außerhalb der Fläche abgeschirmt ist. |
Wenn Du mit "Leiterfläche" die Oberfläche des von mir häufiger erwähnten Leitervolumens meinst, sind wir da einer Meinung!
| Huggy hat Folgendes geschrieben: | | Das Superpositionsprinzip bewirkt aber nicht, dass der Außenraum einer geschlossenen Leiterfläche gegenüber den Feldern von Ladungen im Innenraum abgeschirmt ist. Siehe dazu auch den Wikiartikel zum Faradayschen Käfig. Und das macht deine Argumentation hinfällig. |
Wo bitte habe ich das behauptet? Lies doch Du mal meinen Text nochmal genau:
In Kugelkoordinaten: von r=0 bis R_innen habe ich eine beliebige, festgehaltene (also statische) Ladungsverteilung, von R_innen bis R_außen habe ich einen Leiter (dementsprechend Feldfreiheit) und von R_außen bis unendlich habe ich eben ein Feld, wie wenn eine Punktladung im Zentrum der Hohlkugel wäre, die der integrierten Ladung der Ladungsverteilung im Inneren entspricht.
Wo bitte behaupte ich jetzt, dass das Außenfeld auch verschwinden würde, was Du mir ja offenbar vorwirfst, oder verstehe ich Dich an diesem Punkt falsch???
Ich habe auch geschrieben, wie ich darauf komme: die Ladung bei r=R_innen (also Innenseite) wird sich so verteilen, dass sie ein Feld generiert, das für das Leitervolumen (also im Bereich zwischen R_innen und R_außen) zusammen mit der Ladungsverteilung im inneren (also von r=0 bis r=R_innen) sich gerade aufhebt --> Feldfreiheit.
Und ich habe auch geschrieben: Bei R_außen werden sich Ladungsträger sammeln, die in Summe gerade die Ladungsverteilung bei R_innen aufhebt (Leiter soll ja insgesamt neutral geladen sein).
Sind wir uns soweit wenigstens einig?
Die Frage jetzt ist: Wie ist diese Ladung verteilt? Darauf ist die Antwort eigentlich ziemlich einfach: Sie wird sich homogen verteilen, weil ja von Innen gar kein Feld mehr "zu sehen" ist, weil das schon von der Ladungsverteilung bei R_innen aufgehoben wurde.
Deshalb bleibt von außen gesehen nur noch das Feld von der homogenen Ladungsverteilung auf der äußeren Kugelschale bei R_außen übrig, weil sich durch das Superpositionsprinzip eben alle anderen Ladungsverteilungen gegenseitig aufheben!!!
Ich hab ich keine Ahnung, wie ich das jetzt noch anderes/deutlicher sagen soll. Lies bitte meinen Text erst nochmal genau durch, wenn Du immer noch meinst, ich hätte etwas falsch verstanden oder so...
Gruß
Marco
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 29. März 2014 15:09 Titel: D2 Verfasst am: 29. März 2014 15:09 Titel: |
 |
|
s. mein Vorschlag unten
| Beschreibung: |
|
| Dateigröße: |
14.53 KB |
| Angeschaut: |
10178 mal |

|
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 29. März 2014 15:12 Titel: GvC Verfasst am: 29. März 2014 15:12 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Da die Hohlkugel eine Äquipotentialfläche ist, verteilt sich diese zusätzliche Ladung gleichmäßig auf der Hohlkugel. |
Auf Äquipotentialflächen sind die Ladungen nur in speziellen Fällen gleichmäßig verteilt. Man denke nur an einen Plattenkondensator mit parallel geschichteten Dielektrika unterschiedlicher Permittivität. Da ist die Ladungsdichte auf dem Teil der Kondensatorplatte, die den Bereich mit der größeren Permittivität begrenzt, höher als auf dem Teil der Platte, die an den Bereich mit der kleineren Permittivität grenzt. Dennoch ist die gesamte Plattenoberfläche eine Äquipotentialfläche.
Oder auch im hier vorliegenden Beispiel: Die innere Oberfläche der Kugelschale ist ebenfalls eine Äquipotentialfläche, dennoch ist die Ladung, wie mittlerweile übereinstimmend akzeptiert zu sein scheint, inhomogen verteilt.
Jedenfalls ist die Tatsache, dass es sich bei der äußeren Oberfläche der Hohlkugel um eine Äquipotentialfläche handelt, keine Begründung für eine homogene Ladungsverteilung auf dieser Fläche.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 15:19 Titel: as_string Verfasst am: 29. März 2014 15:19 Titel: |
 |
|
| D2 hat Folgendes geschrieben: | | s. mein Vorschlag unten |
Nein, das ist eindeutig falsch: Das Außenfeld würde so niemals der Laplace-Gleichung genügen!
Gruß
Marco
Zuletzt bearbeitet von as_string am 29. März 2014 15:25, insgesamt einmal bearbeitet |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 15:24 Titel: as_string Verfasst am: 29. März 2014 15:24 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Jedenfalls ist die Tatsache, dass es sich bei der äußeren Oberfläche der Hohlkugel um eine Äquipotentialfläche handelt, keine Begründung für eine homogene Ladungsverteilung auf dieser Fläche. |
Nein, das hat auch keiner behauptet (zumindest soweit ich gelesen habe...)
Aber meine Begründung ist die: Die Ladung auf der Innenfläche verteilt sich gerade so, dass außerhalb dieser Innen-Kugel-Schale kein Feld mehr ist. Deshalb verteilen sich die Ladungen auf der Außenseite aus Symmetriegründen dann homogen!
Das ist für die Außenschale genau so, als ob Du eine Hohlkugel ganz ohne Feld in der Mitte hättest und darauf einen Ladungsüberschuss platzieren würdest. Auch der würde sich homogen auf der Hohlkugel verteilen!
Denk Dir doch mal die Innenseite und die Außenseite der Hohlkugel getrennt, die Innere geerdet und die äußere gerade so geladen, als ob die Ladung, die von der Erdung auf die Innere geflossen wäre, von dieser abgezogen worden wäre. Dann würde zwischen den beiden Kugeln auch kein Feld sein (weil innere Kugel geerdet) und die äußere Kugel wäre in einem feldfreien Raumbereich, so dass sich wieder die Ladungsträger homogen verteilen würden.
Gruß
Marco
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 29. März 2014 15:35 Titel: GvC Verfasst am: 29. März 2014 15:35 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | GvC hat Folgendes geschrieben: | | Jedenfalls ist die Tatsache, dass es sich bei der äußeren Oberfläche der Hohlkugel um eine Äquipotentialfläche handelt, keine Begründung für eine homogene Ladungsverteilung auf dieser Fläche. |
Nein, das hat auch keiner behauptet (zumindest soweit ich gelesen habe...) |
Doch, das hat Huggy behauptet. Ich zitiere ihn/sie nochmal, obwohl ich das bereits in meinem vorigen Beitrag getan habe. (Aber so weit hast Du nach eigener Aussage ja nicht gelesen.)
| Huggy hat Folgendes geschrieben: | | Da die Hohlkugel eine Äquipotentialfläche ist, verteilt sich diese zusätzliche Ladung gleichmäßig auf der Hohlkugel. |
Ich werde auch weder etwas für noch gegen Deine Argumentation sagen, mir war es nur wichtig, auf die offensichtlich falsche Begründung von Huggy hinzuweisen.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. März 2014 16:21 Titel: as_string Verfasst am: 29. März 2014 16:21 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | as_string hat Folgendes geschrieben: | | GvC hat Folgendes geschrieben: | | Jedenfalls ist die Tatsache, dass es sich bei der äußeren Oberfläche der Hohlkugel um eine Äquipotentialfläche handelt, keine Begründung für eine homogene Ladungsverteilung auf dieser Fläche. |
Nein, das hat auch keiner behauptet (zumindest soweit ich gelesen habe...) |
Doch, das hat Huggy behauptet. Ich zitiere ihn/sie nochmal, obwohl ich das bereits in meinem vorigen Beitrag getan habe. (Aber so weit hast Du nach eigener Aussage ja nicht gelesen.)
| Huggy hat Folgendes geschrieben: | | Da die Hohlkugel eine Äquipotentialfläche ist, verteilt sich diese zusätzliche Ladung gleichmäßig auf der Hohlkugel. |
Ich werde auch weder etwas für noch gegen Deine Argumentation sagen, mir war es nur wichtig, auf die offensichtlich falsche Begründung von Huggy hinzuweisen. |
Aber das ist doch auch aus dem Zusammenhang gerissen. Da ging es um die Außenseite der leitenden Hohlkugel und da wird sich die Ladung dann schon homogen verteilen, wenn im Außenbereich keine Ladung mehr ist!
Das ist es ja auch, was ich letztlich sage. Ich weiß an sich nur nicht, was Huggy da noch integrieren will, wenn er selbst schreibt, dass die Ladung im Inneren durch die induzierte Ladung an der Kugelinnenseite nach außen kompensiert wird, dann bleibt doch nur noch die Lasung auf der Außenscjake übrig.
Gruß
Marco
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 29. März 2014 16:32 Titel: D2 Verfasst am: 29. März 2014 16:32 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | D2 hat Folgendes geschrieben: | | s. mein Vorschlag unten |
Nein, das ist eindeutig falsch: Das Außenfeld würde so niemals der Laplace-Gleichung genügen! |
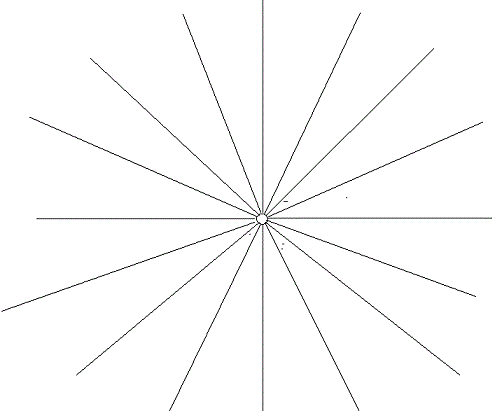
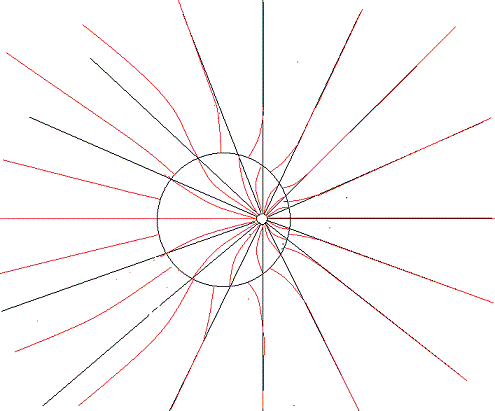
Die Idee ist folgende: Zuerst wird das E Feld einer Ladung gezeichnet.
Diese Ladung wird von einer leitenden Kugel asymmetrisch erfasst.
Die schwarze Hilfslinien werden durch rote Linien ersetzt die das Feld
wie innen so auch außerhalb der Kugel zeichnen.
| Beschreibung: |
|
| Dateigröße: |
7.53 KB |
| Angeschaut: |
10214 mal |
|
| Beschreibung: |
|
| Dateigröße: |
14.27 KB |
| Angeschaut: |
10214 mal |
|
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. März 2014 16:38 Titel: Huggy Verfasst am: 29. März 2014 16:38 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Huggy hat Folgendes geschrieben: | | Da die Hohlkugel eine Äquipotentialfläche ist, verteilt sich diese zusätzliche Ladung gleichmäßig auf der Hohlkugel. |
|
Vielleicht sollte man präziser sagen, man kann zusätzlich zu der induzierten ungleichfömig verteilten Ladung, die die Kugelschale zu einer Äquipotentialfläche macht, eine beliebige weitere Ladung gleichförmig auf der Kugelschale verteilen und diese bleibt dabei eine Äquipotentialfläche. Auf diese Weise kann man der Kugelschale ein beliebiges Potential geben. So steht es im Jackson.
@as_string
Nach deiner Vorstellung hängt das Feld im Außenbereich nur von dieser willkürlich großen gleichförmig verteilten Zusatzladung ab und damit nicht von der gegebenen Punktladung im Innenbereich. Das ist doch inhaltlich identisch mit der Behauptung, dass der Außenraum vom Feld der Ladung im Innenraum durch die Kugelschale abgeschirmt wird.
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 29. März 2014 17:06 Titel: GvC Verfasst am: 29. März 2014 17:06 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | Aber das ist doch auch aus dem Zusammenhang gerissen. Da ging es um die Außenseite der leitenden Hohlkugel und da wird sich die Ladung dann schon homogen verteilen, wenn im Außenbereich keine Ladung mehr ist! |
Eben! Es ging um die Außenseite der Hohlkugel. Und die Begründung von Huggy für eine homogene Ladungsverteilung auf dieser Außenseite war, dass es sich um eine Äquipotentialfläche handele. Und das ist eine falsche Begründung. Nichts anderes habe ich angemerkt.
Du hast eine ganz andere Begründung für die homogene Ladungsverteilung auf der Außenseite der Hohlkugel, zu der ich mich in überhaupt keiner Art und Weise geäußert habe, was ich auch weiterhin so halten werde.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 30. März 2014 11:04 Titel: Huggy Verfasst am: 30. März 2014 11:04 Titel: |
 |
|
@as_string
Habe mir die Sache noch mal durch den Kopf gehen lassen und bin jetzt überzeugt, dass du richtig liegst: Das Feld im Außenbereich entspricht dem Feld einer Punktladung im Zentrum der Hohlkugel. Deine Argumentation mit der Äquipotentialfläche ist zwingend. Im Außenbereich wird für das Potential  eine Lösung gesucht, für die gilt: eine Lösung gesucht, für die gilt:
 =0 \text { für } |\vec r| > R )
=const.)
Das Gaußsche Gesetz wird erfüllt.
Das Feld einer Punktladung im Zentrum der Hohlkugel erfüllt diese Bedingungen. Nach dem Eindeutigkeitssatz ist es die einzige Lösung.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 30. März 2014 15:00 Titel: as_string Verfasst am: 30. März 2014 15:00 Titel: |
 |
|
Ich hab das auch mal geplottet
Gruß
Marco
| Beschreibung: |
|
| Dateigröße: |
12.63 KB |
| Angeschaut: |
8142 mal |

|
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. März 2014 15:02 Titel: jh8979 Verfasst am: 30. März 2014 15:02 Titel: |
 |
|
|
Das sieht an einigen Stellen aus als ob die Feldlinien nicht senkrecht auf der Oberfläche stehen. Aber das liegt vermutlich nur an der Darstellung der Pfeile.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 30. März 2014 15:07 Titel: as_string Verfasst am: 30. März 2014 15:07 Titel: |
 |
|
Ja, das ist halt Gnuplot... 
Der Anfang der Vektorpfeile (also da wo keine Pfeilspitze ist), gibt die Richtung an. Man übergibt dann nur noch ein "dx" und ein "dy", was dann das Ende des Pfeils angibt. Da die Pfeile eine gewisse Länge haben, stimmt dann die Richtung eigentlich nicht mehr am Pfeilende, also da wo die Pfeilspitze ist.
Wäre schön, wenn man gebogene Pfeile oder eben gleich richtige Feldlinien zeichnen könnte...
Gruß
Marco
|
|
 |
|

















 )
)
 )
)