| Autor |
Nachricht |
1
Anmeldungsdatum: 11.11.2012
Beiträge: 1
|
 1 Verfasst am: 11. Nov 2012 14:39 Titel: Kepler Problem/ Lagrange Gleichungen 1 Verfasst am: 11. Nov 2012 14:39 Titel: Kepler Problem/ Lagrange Gleichungen |
 |
|
Meine Frage:
Aufgabe 1 Kepler-Problem
Wir betrachten das Potential V(r) =  /r, /r,
r (� > 0) und verwenden ebene Polarkoordinaten (r,phi)
(aufgrund der Drehimpulserhaltung verlaufen alle Bahnkurven in einer Ebene).
a) Stellen Sie die Lagrange-Funktion und die Lagrange-Gleichungen auf! Reduzieren Sie
das Problem auf eine effektive Gleichung f¨ur r(t) mithilfe der Drehimpulserhaltung
Hallo! Also mit dieser Aufgabe haben wir leider Probleme...
Meine Ideen:
Also wir haben zuerst versucht die Gleichungen mit r in Abhaengigkeit von phi darzustellen, kamen dabei aber nur auf einen riesigen Term der ziemlich falsch aussah 
Ausserdem haben wir auch keine Ahnung wie wir die Drehimpulserhaltung reinbringen sollen. Es gilt ja : 
mit L=  . .
aber wo wir das nun in der Gleichung verwenden koennen...
Waere schoen wenn ihr uns weiterhelfen koenntet. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 11. Nov 2012 15:52 Titel: TomS Verfasst am: 11. Nov 2012 15:52 Titel: |
 |
|
Zunächst mal verlaufen die Bahnen nicht alle in einer Ebene, weil Drehimpulserhaltung gilt. Sondern man kann für eine spezielle Bahn den Drehimpuls in z-Richtung festlegen und dann wird diese eine Bahn in der xy-Ebene verlaufen. Für andere Bahnen kann man andere Ebenen festlegen.
Da die phi-Koordinate zyklisch ist folgt eine Erhaltungsgröße, d.h.

Die letzte Gleichung kann man nach der Winkelgeschwindigkeit auflösen und diese dann die in die Lagrangfunktion einsetzen; damit sind Winkel und Winkelgeschwindigkeit eliminiert, d.h. man hat die Lagrangefunktion auf die eines eindimensionalen Problems reduziert

wobei L_z nur noch als konstanter Parameter fungiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Chuddyholic
Anmeldungsdatum: 18.07.2012
Beiträge: 6
|
 Chuddyholic Verfasst am: 11. Nov 2012 23:15 Titel: Chuddyholic Verfasst am: 11. Nov 2012 23:15 Titel: |
 |
|
hmm also ich hätte jetzt  + \alpha /r ) ... ...
aber wo kommt jetzt der Drehimpuls mit rein?
wie genau meinst du das mit dem nach  umstellen? Damit komme ich leider auch nicht weiter umstellen? Damit komme ich leider auch nicht weiter 
Zuletzt bearbeitet von Chuddyholic am 11. Nov 2012 23:38, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 11. Nov 2012 23:22 Titel: TomS Verfasst am: 11. Nov 2012 23:22 Titel: |
 |
|
Jetzt schreib doch deine Lagrangefunktion L erstmal ordentlich und fehlerfrei in LaTeX (dein letzter Ansatz ist noch nicht ganz korrekt). Mit L meine ich immer die Lagrangefunktion, mit L_z die z-Komponente des Drehimpulses (alle anderen Komponenten verschwinden wenn du die Bahn in die xy-Ebene legst).
Dann berechnest du aus L den von Drehimpuls L_z wie von mir angegeben. Da dieser erhalten (konstant) ist, solltest du anschließend die Gleichung

auflösen

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Chuddyholic
Anmeldungsdatum: 18.07.2012
Beiträge: 6
|
 Chuddyholic Verfasst am: 11. Nov 2012 23:32 Titel: Chuddyholic Verfasst am: 11. Nov 2012 23:32 Titel: |
 |
|
Achso, man könnte ja L ausschreiben -
in Polarkoordinaten wäre
 x x  ) , also , also

und das stelle ich dann nach  um und setzte es in die Lagrangefunktion ein. um und setzte es in die Lagrangefunktion ein.
Aber jetzt hängt 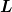 ja auch von ja auch von  ab, und wenn ich die Lagrangefunktion dann nach ab, und wenn ich die Lagrangefunktion dann nach  ableite kommt das ableite kommt das  doch wieder mit rein... doch wieder mit rein... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Nov 2012 07:10 Titel: TomS Verfasst am: 12. Nov 2012 07:10 Titel: |
 |
|
Du meinst im Folgenden offensichtlich L_z; hast du das aus der Euler-Lagrange-Gleichung bzw. als konjugierten Impuls berechnet?

Das löst du jetzt nach 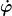 auf und auf und
1) setzt in L ein
2) alternativ berechnest du die Euler-Lagrange-Gleichung für  und setzt und setzt 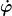 in diese eine (ist eigtl. der korrekte Weg) in diese eine (ist eigtl. der korrekte Weg)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 12. Nov 2012 09:36 Titel: pressure Verfasst am: 12. Nov 2012 09:36 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
1) setzt in L ein
2) alternativ berechnest du die Euler-Lagrange-Gleichung für  und setzt und setzt 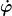 in diese eine (ist eigtl. der korrekte Weg) in diese eine (ist eigtl. der korrekte Weg) |
2) ist nicht nur der bessere Weg. Wenn du 1) ausführst bekommt man einen Vorzeichenfehler, weil man eben nicht in der Lagrangefunktion den konjungierten Impuls von zyklischen Koordinaten durch eine Konstante ersetzen darf.
Was man alternativ machen kann (bei konstanter Energie, also nicht explizit zeitabhängiger Lagrangefunktion), ist bei der Gesamtenergie E=T+V die entsprechende Ersetzung vorzunehmen und dann wiederum die Lagrangefunktion gemäß L=T-V aufzustellen, wobei man den neu erhaltenen Ausdruck mit dem alten Potential zu einem effektive Potential zusammenfasst. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Nov 2012 09:48 Titel: jh8979 Verfasst am: 12. Nov 2012 09:48 Titel: |
 |
|
| pressure hat Folgendes geschrieben: |
2) ist nicht nur der bessere Weg. Wenn du 1) ausführst bekommt man einen Vorzeichenfehler, weil man eben nicht in der Lagrangefunktion den konjungierten Impuls von zyklischen Koordinaten durch eine Konstante ersetzen darf.
Was man alternativ machen kann (bei konstanter Energie, also nicht explizit zeitabhängiger Lagrangefunktion), ist bei der Gesamtenergie E=T+V die entsprechende Ersetzung vorzunehmen und dann wiederum die Lagrangefunktion gemäß L=T-V aufzustellen, wobei man den neu erhaltenen Ausdruck mit dem Potential zu einem effektive Potential zusammenfasst. |
So ein Quatsch... die Euler-Lagrange-Gleichungen sagen genau aus, dass der konjugierte Impuls konstant ist fuer zyklische Variablen. Beide Vorgehensweisen von TomS sind demnach äquivalent... und ob man das im Hamilton-Formalismus rechnet (T+V) oder mit Lagrange (T-V) ist natuerlich auch egal... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Nov 2012 11:07 Titel: TomS Verfasst am: 12. Nov 2012 11:07 Titel: |
 |
|
| pressure hat Folgendes geschrieben: | | 2) ist nicht nur der bessere Weg. Wenn du 1) ausführst bekommt man einen Vorzeichenfehler, ... |
nein, es gibt keinen Vorzeichenfehler, das funktioniert; das Problem kann theoretisch wo anders liegen (z.B. bei Systemen mit Zwangsbedingungen), aber nicht in diesem Fall.
| pressure hat Folgendes geschrieben: | | Was man alternativ machen kann (bei konstanter Energie, also nicht explizit zeitabhängiger Lagrangefunktion), ist bei der Gesamtenergie E=T+V die entsprechende Ersetzung vorzunehmen und dann wiederum die Lagrangefunktion gemäß L=T-V aufzustellen, wobei man den neu erhaltenen Ausdruck mit dem alten Potential zu einem effektive Potential zusammenfasst. |
Im vorliegenden Fall geht es um die Drehimpulserhaltung sowie um das effektive Potential; also betrachten wir L_z und nicht E, das kommt später.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 12. Nov 2012 12:04 Titel: pressure Verfasst am: 12. Nov 2012 12:04 Titel: |
 |
|
Ihr beide seid ja schnell am widersprechen, aber auch ein bisschen zu schnell.
+\frac{\alpha}{r})

Betrachten wir die hier eingeführte Lagrangefunktion 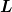 und bilden daraus die Bewegungsgleichung für und bilden daraus die Bewegungsgleichung für  , so erhält man: , so erhält man:

Setzen wir hier nun den Drehimpuls  für für  ein, ergibt sich (die korrekte Bewegungsgleichung): ein, ergibt sich (die korrekte Bewegungsgleichung):

Führen wir die Ersetzung bereits in der Lagrangefunktion durch erhalten wir eine neue Lagrangefunktion

aus der die Bewegungslgeichung
 , ,
resultiert. Und zum Erstaunen von euch beiden, sind die resultierenden Bewegungsgleichungen eben nicht identisch, sondern unterscheiden sich im Vorzeichen des Zentrifugalterm.
Also nochmal zusammengefasst: Es ist unzulässig Erhaltungsgrößen in die Lagrangefunktion einzusetzen. |
|
 |
Chuddyholic
Anmeldungsdatum: 18.07.2012
Beiträge: 6
|
 Chuddyholic Verfasst am: 12. Nov 2012 13:34 Titel: Chuddyholic Verfasst am: 12. Nov 2012 13:34 Titel: |
 |
|
| pressure hat Folgendes geschrieben: |
 , ,
|
super =) das hatte ich am Ende auch raus |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Nov 2012 15:02 Titel: jh8979 Verfasst am: 12. Nov 2012 15:02 Titel: |
 |
|
| pressure hat Folgendes geschrieben: | | Ihr beide seid ja schnell am widersprechen, aber auch ein bisschen zu schnell. |
Da hab ich wohl den Post von TomS nicht genau gelesen. Ich hatte nie vor irgendwas wieder in die Lagrangafunktion einzusetzen. Du hast natuerlich recht, dass man dasn icht machen darf (aber wieso sollte man ueberhaupt auf so eine Idee kommen?  ). ).
Mea culpa. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Nov 2012 22:26 Titel: TomS Verfasst am: 12. Nov 2012 22:26 Titel: |
 |
|
sorry, da hab' ich mich vertan; man darf diese Ersetzung in diesem Fall in der Hamiltonfunktion durchführen, nicht jedoch in der Lagrangefunktion
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|

















 ).
).