| Autor |
Nachricht |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 15:48 Titel: Lagrange Funktion, zwei gleiche Massen m1=m2, Tischplatte Ula Verfasst am: 17. Mai 2014 15:48 Titel: Lagrange Funktion, zwei gleiche Massen m1=m2, Tischplatte |
 |
|
Meine Frage:
Zwei gleiche Massen m1= m2 = m sind durch einen masselosen Faden der Länge l miteinander verbunden, der durch ein Loch in einer reibungsfreien horizontalen Tischplatte verläuft. Die erste Masse gleitet auf dem Tisch, die zweite hängt unter dem Tisch und kann
sich vertikal auf und ab bewegen.
(a) Nehmen Sie an, dass der Faden stets straff bleibt. Stellen Sie dann die Lagrange-Funktion für das System mithilfe der Polarkoordinaten r und 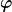 der Masse auf dem Tisch auf. der Masse auf dem Tisch auf.
(b) Stellen Sie die beiden Lagrange-Gleichungen auf und interpretieren Sie die Gleichung mithilfe des Drehimpulses L der ersten Masse
Meine Ideen:
Ich soll die Polarkoordinaten nutzen: r und 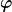 . Nur ich weiß nicht, wo eigentlich . Nur ich weiß nicht, wo eigentlich 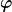 ist und wo r... ist und wo r...
Kann ich annehmen, dass der Faden auf dem Tisch die Länge r hat? Der Winkel 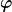 wäre dann, wenn die Masse m1 gleitet... Ist es so? wäre dann, wenn die Masse m1 gleitet... Ist es so?
Nun müsste die Lagrange Funktion der Masse m1 aufgestellt werden.
 + \frac{1}{2} m_{2} (\frac{\dd (l-r)}{\dd t} )² ))
Und )
Aber ich weiß nicht, warum da  steht. steht.
Gruß
Ula |
|
 |
jumi
Gast
|
 jumi Verfasst am: 17. Mai 2014 17:09 Titel: jumi Verfasst am: 17. Mai 2014 17:09 Titel: |
 |
|
Wahrscheinlich ein Tippfehler.
Es muss heißen:
 |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 17:11 Titel: Ula Verfasst am: 17. Mai 2014 17:11 Titel: |
 |
|
|
Ja, stimmt, mit "²". Weiß aber trotzdem nicht, warum das so sein soll |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 17:22 Titel: Ula Verfasst am: 17. Mai 2014 17:22 Titel: |
 |
|
|
Sonst ist T und V richtig? |
|
 |
jumi
Gast
|
 jumi Verfasst am: 17. Mai 2014 17:31 Titel: jumi Verfasst am: 17. Mai 2014 17:31 Titel: |
 |
|
Die Masse auf dem Tisch hat die Radialgeschwindigkeit

und die Tangentialgeschwindigkeit
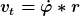
Gesamtgeschwindigkeit mit Pithagoras. |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 17:39 Titel: Ula Verfasst am: 17. Mai 2014 17:39 Titel: |
 |
|
Also dann erhalte ich L:

Ist das richtig? |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 17:50 Titel: Ula Verfasst am: 17. Mai 2014 17:50 Titel: |
 |
|
WEil bei mir m1=m2 = m ist, dann kann ich wohl die unterscheidung zwischen m1 und m2 vermeiden,...

und dann:
) |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 18:18 Titel: Ula Verfasst am: 17. Mai 2014 18:18 Titel: |
 |
|
|
Könnte jemand nachschauen, ob die Rechnung stimmt? Ich bin mir nicht sicher |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 18:34 Titel: Ula Verfasst am: 17. Mai 2014 18:34 Titel: |
 |
|
| Ula hat Folgendes geschrieben: | Also dann erhalte ich L:

Ist das richtig? |
Ich bin mir vor allem unsicher, ob das richtig ist |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 17. Mai 2014 18:55 Titel: as_string Verfasst am: 17. Mai 2014 18:55 Titel: |
 |
|
| Ula hat Folgendes geschrieben: | Also dann erhalte ich L:

Ist das richtig? |
Nein, das ist falsch:
Erstens kommt bei Dir jetzt ja 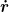 gar nicht mehr vor, obwohl sich doch beide Massen bewegen, wenn sich r verändert, zweitens ist mE Das Vorzeichen beim Potentialterm falsch. gar nicht mehr vor, obwohl sich doch beide Massen bewegen, wenn sich r verändert, zweitens ist mE Das Vorzeichen beim Potentialterm falsch.
[edit: Hab übersehen: 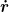 kommt zwar schon vor, aber an einer Stelle, an der eher r stehen sollte und das kommt zwar schon vor, aber an einer Stelle, an der eher r stehen sollte und das 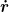 gar keinen Sinn macht!] gar keinen Sinn macht!]
Schau Dir nochmal den Tipp von Jumi mit dem Pythagoras an und überlege Dir auch, mit welcher Geschwindigkeit sich die Masse unter dem Tisch bewegt!
Gruß
Marco |
|
 |
Ula
Gast
|
 Ula Verfasst am: 17. Mai 2014 19:24 Titel: Ula Verfasst am: 17. Mai 2014 19:24 Titel: |
 |
|
Also nochmal zurück zu der kinetischen Energie:
 + \frac{1}{2}m_{2} (.....)²)
²= Ableitung \ von(l-r)?) |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 17. Mai 2014 23:54 Titel: as_string Verfasst am: 17. Mai 2014 23:54 Titel: |
 |
|
Naja, was heißt Ableitung... l ist konstant und das Vorzeichen vor r spielt keine Rolle, weil es so wie so quadriert wird! Du bekommst einfach 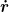 raus. raus.
Stell Dir das doch einfach mal vor: m2 bewegt sich immer so viel hoch und runter, wie das r auf der Tischplatte größer oder kleiner wird. Da spielt es doch gar keine Rolle, wie groß l überhaupt ist.
Die Bewegungsrichtung wird erst wichtig, wenn Du Dir die potentielle Energie anschaust. Aber auch da ist klar: Wird r größer, wandert m2 nach oben. Also ist die potentielle Energie gerade  . Wie lange da l ist, spielt hier auch wieder keine wirkliche Rolle: Wenn l länger ist, dann legt man halt das Nullniveau für die potentielle Energie niedriger. . Wie lange da l ist, spielt hier auch wieder keine wirkliche Rolle: Wenn l länger ist, dann legt man halt das Nullniveau für die potentielle Energie niedriger.
Gruß
Marco |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 09:47 Titel: Ula Verfasst am: 18. Mai 2014 09:47 Titel: |
 |
|
Ok, dann erhalte ich
+ \frac{1}{2} m_{2} \dot{r} ²\\
<br />
V=m_{2}rg)
Und die E.-L.-Gleichungen :
=0\\
<br />
(m_{1}+m_{2} )\ddot{r} - m_{1}r\dot{\varphi } ² + m_{2}g=0
<br />
)
Soll ich dies in dieser Form lassen, oder soll ich m=m1=m2 einsetzten. Ich denke, wenn da m1, m2 steht, dann kann man einfacher interpretieren, oder?
Außerdem:
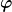 ist zyklisch und der Drehimpuls: ist zyklisch und der Drehimpuls:

Drehimpulserhaltung!
Ist das soweit ok?
Gruß,
Ula |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 09:58 Titel: Ula Verfasst am: 18. Mai 2014 09:58 Titel: |
 |
|
Jetzt kommen noch die Aufgaben c) und d):
c).Drücken Sie  mithilfe von L aus und eliminieren Sie mithilfe von L aus und eliminieren Sie  aus der Gleichung für r . aus der Gleichung für r .
Berechnen Sie nun mit der GLeichung für r den Wert  , bei dem sich die erste Masse entlang einer kreisförmigen Bahn bewegen kann. , bei dem sich die erste Masse entlang einer kreisförmigen Bahn bewegen kann.
d). Nehmen Sie an, die erste Masse bewege sich auf einer kreisförmigen Bahn und würde einen kleinen radialen Stoß erhalten. Setzen Sie =r_{0}+\epsilon (t)) an und schreiben Sie die Gleichung für r mithilfe von an und schreiben Sie die Gleichung für r mithilfe von ) um, indem Sie alle höheren Potenzen von um, indem Sie alle höheren Potenzen von ) vernachlässigen. Zeigen Sie, dass die kreisförmige Bahn stabil ist und dass r(t) sinusförmig um vernachlässigen. Zeigen Sie, dass die kreisförmige Bahn stabil ist und dass r(t) sinusförmig um 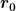 schwingt. Welche Frequenz hat die Schwingung? schwingt. Welche Frequenz hat die Schwingung?
Gruß,
Ula |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Mai 2014 11:28 Titel: as_string Verfasst am: 18. Mai 2014 11:28 Titel: |
 |
|
| Ula hat Folgendes geschrieben: | Ok, dann erhalte ich
+ \frac{1}{2} m_{2} \dot{r} ²\\
<br />
V=m_{2}rg)
Und die E.-L.-Gleichungen :
=0\\
<br />
(m_{1}+m_{2} )\ddot{r} - m_{1}r\dot{\varphi } ² + m_{2}g=0
<br />
)
Soll ich dies in dieser Form lassen, oder soll ich m=m1=m2 einsetzten. Ich denke, wenn da m1, m2 steht, dann kann man einfacher interpretieren, oder?
Außerdem:
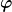 ist zyklisch und der Drehimpuls: ist zyklisch und der Drehimpuls:

Drehimpulserhaltung!
Ist das soweit ok?
Gruß,
Ula |
Ja, das habe ich auch so! 
Ich würde dann schon m1 und m2 durch m ersetzen, aber da Du ja schon alles so gerechnet hast, würde ich das auch ganz am Ende erst machen. Die Gleichungen mit den potentiell unterschiedlichen Massen sind ja allgemeiner und die Gleichsetzung ist hier eher eine Vereinfachung.
Allerdings würde ich dann in der Folge für c) und d) doch eher von einer gleichen Masse m ausgehen, um es da nicht unnötig komplizierter zu machen.
Hast Du Dir schon Gedanken zu c) und d) gemacht?
Ein paar Tipps vielleicht:
In der Gleichung für r kommt ja ein  vor. In L aber ohne Quadrat. vor. In L aber ohne Quadrat.
Am einfachsten ist es wohl, wenn Du die Gleichung für L nach  auflöst und dann einsetzt. auflöst und dann einsetzt.
Was aber dabei interessant ist: Das ist schon wieder so was wie mit dem effektiven Potential! Der einzige größere Unterschied ist, dass zwei Massen bewegt werden müssen (also die kinetische Energie eigentlich doppelt so groß ist), aber sowohl für das Gravitationspotential wie auch für das "Zentrifugal-Potential) jeweils nur eine einzelne Masse zählt. Wenn Du z. B. eine Lagrange-Funktion mit nur einer Variablen r schreiben würdest:
 \dot r^2 - \frac{L}{2mr^2} - mgr) [edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!] [edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!]
Und daraus die Bewegungsgleichung ableitest, siehst Du, dass Du wieder das selbe da stehen hast in r. Wenn Du mal nach dem effektiven Potential schaust, dann wirst Du sehen, dass auch hier wieder dieser "Zentrifugal-Potential"-Term mit L/(2mr²) drin vorkommt.[edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!]
Naja, gut, ich will da jetzt länger drauf rum reiten, weil es ja jetzt nicht wirklich das Thema so genau war...
Die Frage war jetzt nach konstantem r. Das bedeutet ja, dass alle Ableitungen von r nach der Zeit 0 sein müssen. Kannst Du damit schon einen Ausdruck für r in Abhängigkeit von L finden?
Gruß
Marco
Zuletzt bearbeitet von as_string am 18. Mai 2014 21:20, insgesamt einmal bearbeitet |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 12:15 Titel: Ula Verfasst am: 18. Mai 2014 12:15 Titel: |
 |
|
Also die Bewegungsgleichung für r (wenn m1=m2=m):

und

Dann ist:

und

Wenn ich  in die erste Gleichung einsetze, dann erhalte ich in die erste Gleichung einsetze, dann erhalte ich

Außerdem:  Deswegen habe ich: Deswegen habe ich:

Ula |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Mai 2014 12:51 Titel: as_string Verfasst am: 18. Mai 2014 12:51 Titel: |
 |
|
|
Dritte Wurzel |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 12:54 Titel: Ula Verfasst am: 18. Mai 2014 12:54 Titel: |
 |
|
|
Ja, das stimmt |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 13:06 Titel: Ula Verfasst am: 18. Mai 2014 13:06 Titel: |
 |
|
So, und bei der Aufgabe d) habe ich das gegeben:
= r_{0} + \epsilon (t)\\
<br />
r_{0}=\sqrt[3]{\frac{L²}{m²g} } )
Ich weiß jetzt nicht wirklich, wie ich das machen soll...

Ula |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Mai 2014 13:23 Titel: as_string Verfasst am: 18. Mai 2014 13:23 Titel: |
 |
|
Hallo!
Ja, ganz sicher bin ich mir da auch nicht, wie es gemeint ist. Allerdings würde ich das hier "hinein interpretieren":
Du hast ja jetzt:
 [edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!] [edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!]
als Bewegungsgleichung. Bzw. ich sehe gerade, Du hattest das noch durch m geteilt, aber sonst das selbe, wenn ich mich jetzt nicht verschrieben habe.
Ich würde das jetzt so machen: Auf der linken Seite kannst Du ja r direkt durch ) ersetzen. Zweimal ableiten macht daraus einfach ersetzen. Zweimal ableiten macht daraus einfach  . Das war einfach... . Das war einfach...
Auf der anderen Seite kommt r aber im Nenner mit r³ vor. Ich würde jetzt die Taylor-Entwicklung nutzen (und glaube auch, dass das gemeint ist). Und zwar folgende Aufgabe von mir  : :
Entwickle die Funktion  mit Taylor um den Punkt mit Taylor um den Punkt 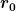 und schreibe gleich und schreibe gleich  . Die Aufgabenstellung legt nahe, dass Du den Terme ab . Die Aufgabenstellung legt nahe, dass Du den Terme ab  und höher vernachlässigen kannst. und höher vernachlässigen kannst.
Dann setze dieses entwickelte r in
 [edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!] [edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!]
ein (statt der eckigen Klammer).[edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!]
Beachte dabei, dass Du schon weißt, welchen Wert  ergibt, nämlich Du hast ja r0 genau so bestimmt, dass das dabei raus kommt.[edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!] ergibt, nämlich Du hast ja r0 genau so bestimmt, dass das dabei raus kommt.[edit: <-- hier fehlt ein Quadrat beim L für den Drehimpuls!]
Wenn Du das hast, steht die Differential-Gleichung für einen harmonischen Oszillator da. Vergleiche die Konstanten mit der normalen Form des harmonischen Oszillators, identifiziere die Konstanten und schau Dir die Lösung für einen harmonischen Oszillator und dessen Schwingungsfrequenz etc. an.
Gruß
Marco
Zuletzt bearbeitet von as_string am 18. Mai 2014 21:21, insgesamt 2-mal bearbeitet |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 17:20 Titel: Ula Verfasst am: 18. Mai 2014 17:20 Titel: |
 |
|
Oh, ich verstehe den ersten Teil nicht wirklich....
Soll ich so einsetzten?

Dann habe ich

Was soll ich nun mit der zweiten Seite machen?
Ula |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 17:45 Titel: Ula Verfasst am: 18. Mai 2014 17:45 Titel: |
 |
|
|
Soll es nicht in deiner Lösung überall L² stehen? |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 18:09 Titel: Ula Verfasst am: 18. Mai 2014 18:09 Titel: |
 |
|
Also ich gehe davon aus, dass da L² steht.
Dann erhalte ich mit der Tayler Entwicklung :

und
= \frac{L²}{mr³} - mg)
Ist das OK?
Gruß
Ula |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Mai 2014 21:17 Titel: as_string Verfasst am: 18. Mai 2014 21:17 Titel: |
 |
|
| Ula hat Folgendes geschrieben: | | Also ich gehe davon aus, dass da L² steht. |
Ja, verdammt... Das hab ich überall vergessen!
| Ula hat Folgendes geschrieben: | Dann erhalte ich mit der Tayler Entwicklung :
 |
Warum eine hoch-minus-4 und dann ein r ohne index-0 im letzten Bruch?
| Ula hat Folgendes geschrieben: | und
= \frac{L²}{mr³} - mg) |
Ja, da musst Du jetzt rechts noch den Bruch durch die Entwicklung von oben ersetzen.
Als Du r0 ausgerechnet hast, da hattest Du doch eine Gleichung verwendet, die Du nach r0 aufgelöst hast. Schau mal, ob Du damit  nicht noch durch etwas ersetzen könntest... nicht noch durch etwas ersetzen könntest...
Gruß
Marco |
|
 |
Ula
Gast
|
 Ula Verfasst am: 18. Mai 2014 22:56 Titel: Ula Verfasst am: 18. Mai 2014 22:56 Titel: |
 |
|
|
Klar. Ohne minus und mit ro. |
|
 |
Ula
Gast
|
 Ula Verfasst am: 20. Mai 2014 07:14 Titel: Ula Verfasst am: 20. Mai 2014 07:14 Titel: |
 |
|
No eine Frage. Soll ich wirklich so einsetzten?

Dann habe ich

Oder eher so:

Dann habe ich
 |
|
 |
Ula
Gast
|
 Ula Verfasst am: 20. Mai 2014 08:16 Titel: Ula Verfasst am: 20. Mai 2014 08:16 Titel: |
 |
|
Also ich gehe zuerst davon aus, dass:

Dann habe ich :
=\frac{L²}{mr_{0}^{3} } - \frac{3L²}{mr_{0}^{4} } \cdot \epsilon - mg)

(nach der Aufgabe c): kreisförmige Bewegung)
=\frac{L²}{mr_{0}^{3} } - \frac{3L²}{mr_{0}^{4} } \cdot \epsilon - mg\\
<br />
<br />
\ddot{\epsilon } (t)= mg - \frac{3L²}{mr_{0}^{4} } \cdot \epsilon - mg\\
<br />
\ddot{\epsilon } (t)=- \frac{3L²}{mr_{0}^{4} })
Substitution:

Ist das so ok?
Gruß
Ula |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 20. Mai 2014 11:56 Titel: as_string Verfasst am: 20. Mai 2014 11:56 Titel: |
 |
|
| Ula hat Folgendes geschrieben: | =- \frac{3L²}{mr_{0}^{4} }) |
Hier fehlt das epsilon auf der rechten Seite.
| Ula hat Folgendes geschrieben: | | Ist das so ok? |
Soweit ich das Ende jetzt zumindest grob überflogen habe, denke schon...
Kannst Du jetzt das  irgendwie mit dem irgendwie mit dem  vom harmonischen Oszillator identifizieren? vom harmonischen Oszillator identifizieren?
Gruß
Marco |
|
 |
Ula
Gast
|
 Ula Verfasst am: 20. Mai 2014 19:13 Titel: Ula Verfasst am: 20. Mai 2014 19:13 Titel: |
 |
|
Ich kann auch so schreiben:

Dann habe ich :

Nun weiß ich nicht, wie die Lösung der DGl ist. Irgendwas in der Form:
= \epsilon_{0} \sin(\omega_{ o}(t)+\varphi ) )
Sieht man, dass die kreisförmige Bahn sinusförmig schwingt.
Und die Frequenz ist:

Ist das ok?
Gruß,
Ula |
|
 |
Ula
Gast
|
 Ula Verfasst am: 20. Mai 2014 20:04 Titel: Ula Verfasst am: 20. Mai 2014 20:04 Titel: |
 |
|
Sorry, das war nun falsch:
"Sieht man, dass die kreisförmige Bahn sinusförmig schwingt. "
 + \varphi ) )
Man sieht, dass r(t) sinusförmig schwingt. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 20. Mai 2014 20:22 Titel: as_string Verfasst am: 20. Mai 2014 20:22 Titel: |
 |
|
| Ula hat Folgendes geschrieben: | Ich kann auch so schreiben:

|
Das Minus ist doch falsch. Und warum schreibst Du eigentlich nicht gleich omega, wenn Du schon das Quadrat nimmst. Omega aber nicht komplex und alle Konstanten in der Gleichung sind positive Zahlen.
Gruß
Marco |
|
 |
Ula
Gast
|
 Ula Verfasst am: 20. Mai 2014 20:28 Titel: Ula Verfasst am: 20. Mai 2014 20:28 Titel: |
 |
|
Ja! Klar, ohne minus. Falsch getippt. Sonst alles richtig?
Ula |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 20. Mai 2014 20:41 Titel: as_string Verfasst am: 20. Mai 2014 20:41 Titel: |
 |
|
Soweit sieht alles gut aus, würde ich sagen!  Zumindest habe ich das auch raus, könnte natürlich trotzdem falsch sein, wer weiß... Zumindest habe ich das auch raus, könnte natürlich trotzdem falsch sein, wer weiß...
Noch eine Sache würde ich aber schreiben: Du sollst ja zeigen, dass die Bahn "stabil" ist, dass also bei r0 ein stabiles Gleichgewicht herrscht. Das kannst Du damit begründen, dass die Beschleunigung immer entgegen gesetzt zur Auslenkung ist, also immer zurück treibt zu r0. So wie es eben auch bei einem harmonischen Oszillator der Fall ist. Deshalb ist das Minus wichtig, wenn Du  auf der einen und auf der einen und  auf der anderen Seite stehen hast (also entgegen gesetztes Vorzeichen von Auslenkung zu Beschleunigung), oder eben ein Plus, wenn Du es auf einer Seite stehen hast. auf der anderen Seite stehen hast (also entgegen gesetztes Vorzeichen von Auslenkung zu Beschleunigung), oder eben ein Plus, wenn Du es auf einer Seite stehen hast.
Wäre das nicht so, dann wäre es ein instabiles Gleichgewicht und bei der geringsten Störung auch der Gleichgewichtslage, würde r entweder immer größer oder immer kleiner werden, aber nicht mehr zu r0 zurück kehren.
Gruß
Marco |
|
 |
Ula
Gast
|
 Ula Verfasst am: 20. Mai 2014 20:55 Titel: Ula Verfasst am: 20. Mai 2014 20:55 Titel: |
 |
|
D A N K E!!!

Gruß,
Ula |
|
 |
|


















 :
:
 Zumindest habe ich das auch raus, könnte natürlich trotzdem falsch sein, wer weiß...
Zumindest habe ich das auch raus, könnte natürlich trotzdem falsch sein, wer weiß...