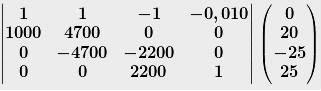| Autor |
Nachricht |
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
 Elektronik91 Verfasst am: 22. Mai 2015 16:16 Titel: Umformen von Gleichungen bei Kirchhoffscher Berechnung |
 |
|
Hallo zusammen,
ich bin neu hier im Forum.
Ich habe ein großes Problem mit dem umstellen von Gleichungen bei einer Kirchhoffschen -Schaltungsberechnung.
Die Kirchhoffschen Regeln sind mir klar und ich habe auch kein Problem damit die Knoten und Maschengleichungen aufzustellen.
Mein Problem ist das Eliminieren der unbekannten durch umformen der Gleichungen.
Hier das Beispiel:
Gegeben: Uq1 = 10V, Uq2 = 5V, R1 = 100Ohm, R2 = 220Ohm, R3 = 1k Ohm, R4 = 1kOhm
Gesucht wird: I, I3, I4
Nun zu den 3 Gleichungen:
Knoten: 
Masche 1: 
Masche 2: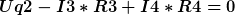 
Als erstes habe ich die Masche 1 nach I3 umgeformt.
Als nächstes kann ich die umgeformte Gleichung in die 1 & 2 Gleichung einsetzen (Knoten & Masche 2).
Neue Knotengleichung: 
Neue Maschengleichung 2:  + I*R1 + I*R2 -Uq2}{R3} *R3 + I4*R4 = 0)
Ab hier komme ich nicht mehr weiter.
In der Knotengleichung habe ich I auf der rechten und linken Seite, weiters habe ich I4 auch noch als unbekannte.
Bei der neuen Maschengleichung 2 habe ich ebenfalls zwei unbekannte (I & I4).
Ich verstehe einfach nicht wie ich da weiter machen sollte.
Ich bitte euch um Hilfe!!
MfG
|
|
 |
erkü
Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
| erkü Verfasst am: 22. Mai 2015 19:06 Titel: |
|
|
Hey !
Zur Wahrung der Übersicht bringt man die gesuchten Größen auf eine Seite (z.B. links) der Gleichung, wie
I+R_3I_3=U_1+U_2\\\cdots)
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk:
Zuletzt bearbeitet von erkü am 24. Mai 2015 00:18, insgesamt einmal bearbeitet |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 23. Mai 2015 20:54 Titel: |
|
|
|
Und wie würde man es mit einer normalen Umformung machen?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 23. Mai 2015 21:43 Titel: |
|
|
|
Genauso... aber es systematisch zu machen ist einfach praktischer...
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 23. Mai 2015 21:50 Titel: |
|
|
| Elektronik91 hat Folgendes geschrieben: | | Und wie würde man es mit einer normalen Umformung machen? |
Natürlich geht es immer auch mit den unterschiedlichsten Methoden - es muss ja immer das Gleiche rauskommen. Ich schau mal Deine Ergebnisse durch.
Aber das Problem ist meistens nur die fehlende Kontrollmöglichkeit bei den umfangreichen Gleichungssystemen. Außerdem sollte man möglichst wenig schreiben, da man leicht Zahlendreher und dgl. bekommt.
Dies ist der Grund, warum man mehr mechanische Verfahren nutzt, die sich leicht überprüfen lassen.
Hier kannst gut nachverfolgen, wie man die Kirchhoffgleichungen effizient löst.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 23. Mai 2015 22:21 Titel: Re: Umformen von Gleichungen bei Kirchhoffscher berechnung |
|
|
ja ....
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:22, insgesamt 2-mal bearbeitet |
|
|
erkü
Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
| erkü Verfasst am: 24. Mai 2015 00:32 Titel: Re: Umformen von Gleichungen bei Kirchhoffscher berechnung |
|
|
| isi1 hat Folgendes geschrieben: |
...
Per Matrix gehts leichter:
| Code: | [code]Ordnen
I I3 I4 =
1 -1 -1 0
R1+R2 R3 0 Uq1+Uq2
0 -R3 R4 Uq2
...[/code][
1 -1 -1 0
R1+R2 R3 0 Uq1+Uq2
0 -R3 R4 Uq2
... |
|
| Code: |
1 -1 -1 0
R1+R2 R3 0 Uq1+Uq2
0 -R3 R4 - Uq2
... |
(s. Themenstart)
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 24. Mai 2015 07:33 Titel: |
|
|
so ....
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:23, insgesamt 2-mal bearbeitet |
|
|
erkü
Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 24. Mai 2015 16:38 Titel: |
|
|
Sehr gut, Erkü
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:24, insgesamt einmal bearbeitet |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 27. Mai 2015 11:23 Titel: |
|
|
Danke erstmals für die Hilfe.
Ich habe es jetzt mal selbst versucht die Matrix nach dem Gauß-Verfahren zu lösen. Doch leider weicht mein Ergebnis vom Richtigen ab.
Hier meine Lösung:
Hier mache ich nichts anderes als die 0,32 aus der zweiten Zeile mit der ersten Zeile zu multiplizieren und anschließen die erste Zeile mit der zweiten Zeile zu addieren. Die 0,32 mache ich zuerst negativ.
Dasselbe mache ich auch mit der dritten Zeile.
Nun sieht die Matrix so aus:
Jetzt multipliziere ich -1 aus der 3. Zeile mit der 2. Zeile:
Nun nehme ich die 1,32 aus der dritten Zeile und setze ein minus davor
-1,32 und multipliziere es anschließend wieder mit der 2. Zeile:
Jetzt bin ich mit der Matrix berechnung fertig.
Im nächsten Schritt muss ich jetzt meine drei Zeilen nur mehr umformen:
Zeile 3:
Was mache ich Falsch?
Das Ergebnis sollte lauten 5,12mA, mein Ergebnis ist dazu noch negativ??
MfG
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 27. Mai 2015 14:57 Titel: |
|
|
Prima ...
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:24, insgesamt einmal bearbeitet |
|
|
erkü
Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 03. Jun 2015 18:42 Titel: |
|
|
Als erstes möchte ich euch für eure Hilfe danken!!
Ich habe jetzt ein paar Beispiele erfolgreich durchgerechnet!
Nur bei einem Beispiel stimmt meine Lösung nicht.
Bei diesem Beispiel wird der Widerstandswert für den Widerstand R4 gesucht, wenn durch Ihn ein Strom von 10mA fließt.
Geg: Uq1 = 20V, Uq2 = 25V, R1 = 1k, R2 = 4,7k, R3 = 2,2k, I4 = 10mA
In diesem Beispiel gibt es zwei Knoten die zu einem zusammengefasst wurden.
Knoten: I1 + I3 = I2 + I4
M1: I1*R1+I2*R2 = Uq1
M2: -I2*R2-I3*R3 = -Uq2
M3: I3*R3+I4*R4 = Uq2
Ich habe anschließend eine Umformung für die Matrix durchgeführt.
So sieht meine Matrix aus:
für R4 sollte 1,28kOhm herauskommen, tut es aber leider nicht.
Ich habe meine Matrix zur Sicherheit mal in den online Rechner eingetippt und dieser hat auch nicht das richtige Ergebnis errechnet.
Was mache ich falsch?
MfG
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 03. Jun 2015 18:58 Titel: |
|
|
Die Methoden Maschenstrom- und Knotenpotentialverfahren sind ausgeprochen sicher für solche Aufgaben
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:25, insgesamt 3-mal bearbeitet |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 03. Jun 2015 18:59 Titel: |
|
|
|
Um welche Schaltung geht es denn?
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 04. Jun 2015 09:14 Titel: |
|
|
Hier die Schaltung:
V1 = Uq1
V2 = Uq2
| Beschreibung: |
|
Download |
| Dateiname: |
Schaltung.jpg |
| Dateigröße: |
64.55 KB |
| Heruntergeladen: |
366 mal |
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 04. Jun 2015 10:39 Titel: |
|
|
Die Lösung erfordert wirklich nicht mehr Schreiberei, als unter dem Bild.
| Beschreibung: |
|
Download |
| Dateiname: |
Schaltung.png |
| Dateigröße: |
142.75 KB |
| Heruntergeladen: |
354 mal |
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 07. Jun 2015 12:50 Titel: |
|
|
Wie kommt Ihr auf so eine Matrix:
i1 ik2 i4
5,7 -4,7 0 20
-4,7 6,9 -2,2 -25
0 0 1 10
wenn ich Sie aufstelle, sieht Sie so aus (Siehe Bild: Matrix)
MfG
| Beschreibung: |
|
| Dateigröße: |
6.68 KB |
| Angeschaut: |
7680 mal |
|
|
|
|
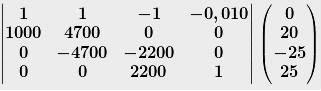
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 07. Jun 2015 14:45 Titel: |
|
|
| Elektronik91 hat Folgendes geschrieben: | Wie kommt Ihr auf so eine Matrix:
i1 ik2 i4
5,7 -4,7 0 20
-4,7 6,9 -2,2 -25
0 0 1 10 |
Ganz simpel - siehe: forum.physik-lab.de/ftopic37.html
Links Kreisstrom i1, in der Mitte oben nach rechts ik2 und rechts eingeprägt i4=10mA.
1. Zeile: 5,7k=4,7k+1k ... die Widerstände im linken Kreis
Kopplung zum 2. Kreis: -4,7 und mit rechts keine Kopplung, deshalb die Null.
Als Spannung kommt rechts 20 hinzu, die V1
2. Zeile: gleiches Verfahren: Kopplung zum 1. Kreis die schon erwähnten -4,7
Summe der Widerstände im Kreis 4,7 + 2,2 = 6,9 und Kopplung nach rechts -2,2k. Bleibt noch die Spannung mit -25V, da Kreisstrom und Spannungspfeil in gleiche Richtung weisen.
3. Zeile sagt nur, dass der rechte Kreisstrom 10 mA ist
Alles klar?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 07. Jun 2015 19:10 Titel: |
|
|
Du verwendest also das Maschenstromverfahren.
Wie löse ich dies mit der Knoten & Maschenregel?
Danke!
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 07. Jun 2015 19:44 Titel: |
|
|
Genau so, Du darfst nur keine falschen Gleichungen eingeben. Die Matrix sieht dann zwar etwas anders aus, aber R4 sollte bei jedem beliebigen Verfahren gleich groß werden.
Dieses Kreisstromverfahren und auch das Knotenpotentialverfahren verwenden die gleichen Regeln, nur hat man sich dabei Gedanken gemacht, wie man das möglichst fehlerfrei, möglichst einfach und möglichst ohne langes Nachdenken durchführen kann.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 07. Jun 2015 19:55 Titel: |
|
|
gelösct
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:27, insgesamt einmal bearbeitet |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 07. Jun 2015 21:23 Titel: |
|
|
Da ist mir beim Formeleditor ein Fehler passiert. Sorry.
Es handel sich hierbei um eine ganz normale Koeffizientenmatrix.
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 07. Jun 2015 21:48 Titel: |
|
|
| Elektronik91 hat Folgendes geschrieben: | Da ist mir beim Formeleditor ein Fehler passiert. Sorry.
Es handel sich hierbei um eine ganz normale Koeffizientenmatrix. |
Aber ist das so
Matrix * (I1|I2|I3|I4)' = (0|20|-25|25)'
gemeint?
Jedenfalls verstehe ich schon die 1. Zeile der Matrix nicht. Erklär mal, bitte.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 08. Jun 2015 15:08 Titel: |
|
|
In der ersten Zeile habe ich einfach das selbe gemacht wie bei meinem ersten Beispiel in diesem Beitrag.
Ich habe in der ersten Zeile der Matrix meine Knotengleichung eingesetzt.
Vorher habe ich die Knotengleichung so umgeformt, das die Summe der Ströme gleich Null ergibt.
Deshalb sieht meine Knotengleichung in der Matrix so aus:
I1 + I3 - I2 - I4 = 0
Ich dachte mir ich muss das so machen, da wir es im anderen Beispiel auch so gemacht haben?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 08. Jun 2015 15:42 Titel: |
|
|
| Elektronik91 hat Folgendes geschrieben: | Deshalb sieht meine Knotengleichung in der Matrix so aus:
I1 + I3 - I2 - I4 = 0
|
Nein, was Du hingeschrieben hast, ist
Hattest Du nicht selber gesagt, dass es sich um eine Koeffizientenmatrix handelt? Dann stehen in der ersten Zeile die Koeffizienten der Ströme. Wie kommst Du auf den seltsamen Koeffizienten von I4?
Im Übrigen würde ich hier das Knotenspannungsverfahren anwenden. Dann besteht die zu lösende Matrizengleichung aus einer einzigen Zeile, und Du hast das richtige Ergebnis (R4=1,2 kOhm) in zwei Zeilen.
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 08. Jun 2015 15:58 Titel: |
|
|
gelöscht
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 19:27, insgesamt einmal bearbeitet |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 08. Jun 2015 18:09 Titel: |
|
|
Nochmals zur Wiederholung:
Die Knotengleichung kommt schon so wie ich es mir gedacht habe immer in die erste Zeile. Da aber I4 bereits bekannt ist, wandert es in die Spalte in der auch die Spannungen stehen.
An der ursprünglichen stelle von I4 schreibe ich nun eine 0 hin, da I4 ja nach rechts gewandert ist.
Wenn ich an die ursprüngliche stelle von I4, R4 hinschreiben würde, dann müsste ich ja eine 1 hinschreiben und keine 0 oder?
0 bedeutet ja das hier keine Variable vorhanden ist.
1 bedeutet, das hier eine Variable vorhanden ist deren Wert aber nicht bekannt ist.
Nochmals vielen dank für Deine bemühungen!!
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 09. Jun 2015 08:47 Titel: |
|
|
Ganz falsch ist das nicht, aber besser, Du vergegenwärtigst Dir immer die normal geschriebene Gleichung, für die die Matrixzeile steht. Die Matrix ist ja nur eine Abkürzungsschreibweise des (geordneten) Gleichungssystems.
Schau Dir im Mathebuch oder Internet die Multiplikation von Matrizen an.
Kurz:
Jede Spalte enthält die Multiplikatoren für die zur Spalte gehörenden Unbekannten.
Für den Gauß-Jordan-Algorithmus fügt man rechts noch den Ergebnisvektor an.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 09. Jun 2015 19:30 Titel: |
|
|
Es hat ja grundsätzlich alles gepasst, bis auf den kleinen Fehler.
Wenn ich immer gleich vorgehe und die Gleichungen so schreibe:
1. Knotengleichung
2. Maschengleichungen
Hinweis:
(Natürlich muss jetzt eine passende Umformung durchgeführt werden.)
dann sollte es keine Probleme geben.
Vielen dank nochmals für eure Hilfe!!
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 10. Jun 2015 17:24 Titel: |
|
|
Wenn bei diesem Beispiel (nur zum Verständnis) I3 & I4 bekannt wären (z.B. I3 = 5mA & I4 = 10mA), dann müsste die erste Zeile der Matrix so aussehen:
einsetzen der Werte:
MfG
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 10. Jun 2015 19:40 Titel: |
|
|
| Elektronik91 hat Folgendes geschrieben: | Wenn bei diesem Beispiel (nur zum Verständnis) I3 & I4 bekannt wären (z.B. I3 = 5mA & I4 = 10mA), dann müsste die erste Zeile der Matrix so aussehen:
einsetzen der Werte:
|
Schwer zu sagen, Elektronik91, wenn Du den Vektor der Unbekannten nicht verrätst.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 11. Jun 2015 19:54 Titel: |
|
|
Meine Frage bezieht sich auf das zuletzt angesprochene Beispiel:
Knoten: I1 + I3 = I2 + I4
M1: I1*R1+I2*R2 = Uq1
M2: -I2*R2-I3*R3 = -Uq2
M3: I3*R3+I4*R4 = Uq2
Nur jetzt ist auch I3 bekannt, sonst ist alles gleich.
MfG
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 13. Jun 2015 19:13 Titel: |
|
|
|
Ist das so korrekt wie ich mir das gedacht habe??
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 13. Jun 2015 19:17 Titel: |
|
|
| Elektronik91 hat Folgendes geschrieben: | | Ist das so korrekt wie ich mir das gedacht habe?? |
Welches sind denn dann die Unbekannten? | isi1 hat Folgendes geschrieben: | | Schwer zu sagen, Elektronik91, wenn Du den Vektor der Unbekannten nicht verrätst. |
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 07. Jul 2015 18:07 Titel: |
|
|
Sorry, das ich mich länger nicht mehr gemeldet habe. Hatte eine wichtige Prüfung in Mathe.
Zu meinen letzten Post:
Dieses Beispiel dient nur zum Verständnis.
Ich habe hier einfach das letzte Beispiel herangenommen und zusätzlich eine bekannte hinzugefügt:
Knoten: I1 + I3 = I2 + I4
M1: I1*R1+I2*R2 = Uq1
M2: -I2*R2-I3*R3 = -Uq2
M3: I3*R3+I4*R4 = Uq2
Es ist alles gleich wie beim letzten Beispiel, bis auf I3. I3 ist jetzt keine unbekannte mehr. I3 = 5mA. I4 war im letzten Beispiel auch schon bekannt. I4 = 10mA
Dann müsste die erste Zeile der Matrix so aussehen:
einsetzen der Werte:
Ich muss ja die bekannten Größen auf die rechte Seite bringen und die unbekannten Größen auf die linke Seite.
Ich bitte euch mir das zu Bestätigen, wenn es stimmt. Damit ich mir sicher sein kann, das ich das Verstanden habe.
MfG und Danke!!
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 09. Jul 2015 11:31 Titel: |
|
|
Ich bitte euch um eine Antwort.
Danke!!
|
|
|
Elektronik91
Anmeldungsdatum: 22.05.2015
Beiträge: 51
|
| Elektronik91 Verfasst am: 16. Jul 2015 22:54 Titel: |
|
|
|
Ich bitte euch nochmals um eine Antwort.
|
|
|
|
Registrieren
Login
FAQ
Suchen
