| Autor |
Nachricht |
die.fly

Anmeldungsdatum: 03.11.2011
Beiträge: 121
|
 die.fly Verfasst am: 23. März 2012 23:49 Titel: Frage zu den "Deltas" die.fly Verfasst am: 23. März 2012 23:49 Titel: Frage zu den "Deltas" |
 |
|
Irgendwie gibts immer verschiedene Deltas. Ist das alles das selbe oder??
Also es gibt ja:
d
Δ
δ
Beim Nablaoperator nimmt man ja bsw. das δ.
hier wieder d

 = \frac{\mathrm{d}Q}{\mathrm{d}V})
_________________
Physikstudent 2tes Semester |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 24. März 2012 01:15 Titel: MI Verfasst am: 24. März 2012 01:15 Titel: |
 |
|
Da haben wir wieder das Problem, dass die Physiker die Mathematik so malträtieren, wie sie möchten - bzw. einfach mal drauflos hantieren, ohne genau zu wissen, was dahintersteckt. Aber sonst kommt man halt nicht voran...
Zunächst:  ist der Nablaoperator, nicht ist der Nablaoperator, nicht  . .
Dann fangen wir mal an:
 ist der Nablaoperator und fasst den Vektor der partiellen Ableitungen einer skalaren Funktion (z.B. ein Potential) zusammen. Manchmal sieht man auch den Nablaoperator auf eine vektorwertige Funktion angewendet - da bezeichnet er dann so etwas wie die Matrix der ersten Ableitungen. ist der Nablaoperator und fasst den Vektor der partiellen Ableitungen einer skalaren Funktion (z.B. ein Potential) zusammen. Manchmal sieht man auch den Nablaoperator auf eine vektorwertige Funktion angewendet - da bezeichnet er dann so etwas wie die Matrix der ersten Ableitungen.
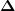 hat (mindestens) zwei Bedeutungen. hat (mindestens) zwei Bedeutungen.
Die erste (und einfachste) ist die des Laplaceoperators. Der Laplaceoperator ist ein Differentialoperator, der z.B. in der Poissongleichung auftritt und ist nichts anderes als die Spur der Hessematrix (Matrix der zweiten Ableitungen einer skalaren Funktion eines Vektors - z.B. des Potentials).
Also in kartesischen Koordinaten für )

wobei das  für die partielle Ableitung steht, was du vermutlich weißt. für die partielle Ableitung steht, was du vermutlich weißt.
In anderen Koordinaten sieht das Ding dann völlig anders aus. In der Form könnte man (mehr formal) auch schreiben 
Die zweite Bedeutung von 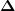 ist die als Änderungsrate. Zum Beispiel in Form einer Geschwindigkeitsänderung: ist die als Änderungsrate. Zum Beispiel in Form einer Geschwindigkeitsänderung:  Änderung der Geschwindigkeit ist Beschleunigung mal zeitliche Änderung. Änderung der Geschwindigkeit ist Beschleunigung mal zeitliche Änderung. 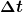 ist dabei ein kleines Zeitintervall - klein, aber endlich. Man hat zum Beispiel: ist dabei ein kleines Zeitintervall - klein, aber endlich. Man hat zum Beispiel:  - die Formel zur Berechnung der Steigung. Wenn man jetzt formal - die Formel zur Berechnung der Steigung. Wenn man jetzt formal 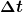 gegen Null gehen lässt, dann hätte man die Ableitung: gegen Null gehen lässt, dann hätte man die Ableitung:  in Leibnitzschreibweise. in Leibnitzschreibweise.
Im Grunde müssten Physiker fast immer mit diesen Deltas anfangen und dann den Grenzübergang nach ihren ganzen Rechnungen machen - tun sie aber nicht, weil's lästig ist und (fast) nie schiefgeht.
Nächstes d: Jetzt kommen wir zu  . Da wird's haarig - Mathematiker kriegen da gerne einen Koller (siehe MatheBoard), wie Physiker mit dem Ding umspringen. . Da wird's haarig - Mathematiker kriegen da gerne einen Koller (siehe MatheBoard), wie Physiker mit dem Ding umspringen.
Eine Möglichkeit ist folgende: 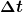 ist, wie ich gesagt habe, meist "sehr klein, aber endlich" zu verstehen. Wenn man jetzt also das ganze infinitesimal werden lässt, dann kommt man zu ist, wie ich gesagt habe, meist "sehr klein, aber endlich" zu verstehen. Wenn man jetzt also das ganze infinitesimal werden lässt, dann kommt man zu 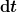 - Im Grunde handelt es sich also bei solchen Dingen um infinitesimale Größen (also Größen, die kleiner sind, als jede Zahl, aber größer als Null). In dieser Form: - Im Grunde handelt es sich also bei solchen Dingen um infinitesimale Größen (also Größen, die kleiner sind, als jede Zahl, aber größer als Null). In dieser Form:

ist das dann eine Summation dieser infinitesimalen Größen.
Sprich (um zum Beispiel mit der Geschwindigkeit zurückzukommen):
 für endliche Zeitabstände wird beim Grenzübergang für endliche Zeitabstände wird beim Grenzübergang
 für infinitemsimale Zeitabstände. So (oder so ähnlich) hat Leibnitz das ursprünglich eingeführt, denn das Integralzeichen steht ja für "Summe". für infinitemsimale Zeitabstände. So (oder so ähnlich) hat Leibnitz das ursprünglich eingeführt, denn das Integralzeichen steht ja für "Summe".
In der Vektorschreibweise (dein Beispiel) gibt es dann einfach Regeln, wie man das ganze in gewöhnliche Integrale umwandelt (siehe "Wegintegrale" und "Integrale über Oberflächen"). Das sind Dinge, die eigentlich im ersten Semester theoretische Physik besprochen werden.
Das (infinitesimale Objekte) ist für die Vorstellung in der Physik meist ausreichend, mathematisch aber extrem kompliziert - möchte man den Ansatz vernünftig machen, muss man die sogenannte "Nichtstandardanalysis" betreiben, die - wie der Name sagt - eben "Nichtstandard" ist.
Mathematisch muss man da anders rangehen: Zunächst gibt es Dinge wie  - das ist einfach die Leibnitzschreibweise für eine Ableitung. - das ist einfach die Leibnitzschreibweise für eine Ableitung.
Der Physiker nutzt das auch so, macht aber noch einen kleinen Unterschied: Während er mit  ganz normal die partielle Ableitung bezeichnet, bezeichnet er mit ganz normal die partielle Ableitung bezeichnet, bezeichnet er mit  gerne die sog. totale Ableitung. Gemeint ist, dass nicht nur nach der "expliziten Zeitabhängigkeit" abgeleitet wird, sondern auch nach allen impliziten Abhängigkeiten. Nehmen wir beispielsweise an, du hast eine Größe gerne die sog. totale Ableitung. Gemeint ist, dass nicht nur nach der "expliziten Zeitabhängigkeit" abgeleitet wird, sondern auch nach allen impliziten Abhängigkeiten. Nehmen wir beispielsweise an, du hast eine Größe 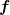 gegeben, die von den Ortskoordinaten deines Teilchens abhängt und nochmal von der Zeit, also gegeben, die von den Ortskoordinaten deines Teilchens abhängt und nochmal von der Zeit, also ) . Die explizite Zeitabhängigkeit ist das t hinten drin. Nun hängt aber die Position des Teilchens in der Regel AUCH von der Zeit ab - das ist die implizite Zeitabhängigkeit, d.h.: . Die explizite Zeitabhängigkeit ist das t hinten drin. Nun hängt aber die Position des Teilchens in der Regel AUCH von der Zeit ab - das ist die implizite Zeitabhängigkeit, d.h.: ,x_2(t),x_3(t),t)) . Für die totale Zeitableitung muss man jetzt per Kettenregel nach allem ableiten. Konkret: . Für die totale Zeitableitung muss man jetzt per Kettenregel nach allem ableiten. Konkret:

So, das war jetzt die Ableitung.
Wenn das  jetzt alleine steht (und alleine meine ich: Nicht im Integral!), dann ist das mathematisch gesehen etwas ganz anderes - nämlich ein Differential. Deswegen darf man die Teile (in der Mathematik) auch nicht einfach hin- und herschmeißen, dadurch teilen, etc. Ein Differential im Nenner ergibt keinen Sinn! jetzt alleine steht (und alleine meine ich: Nicht im Integral!), dann ist das mathematisch gesehen etwas ganz anderes - nämlich ein Differential. Deswegen darf man die Teile (in der Mathematik) auch nicht einfach hin- und herschmeißen, dadurch teilen, etc. Ein Differential im Nenner ergibt keinen Sinn!
Ein Differential ist nun ein Objekt aus der Differentialgeometrie und ist so etwas wie eine Ableitung - allerdings verändert es das Objekt. Das Zauberwort hier sind "Differentialformen". Kurz gesagt sind Differentialformen antisymmetrische Tensoren (jetzt auf diff'baren Mannigfaltigkeiten), aber das bringt dir vermutlich nichts. Leider habe ich auch keine ganz einfache Erklärung zur Hand, nur folgendes:
- Eine skalare Funktion (diff'bar) ist eine Differentialform nullter Ordnung.
- Eine vektorwertige Funktion ist so etwas wie eine Differentialform erster Ordnung (in gewisser Weise, eigentlich verhält sich eine Funktion etwas anders...).
- Das  erhöht die Ordnung der Differentialform um eins. erhöht die Ordnung der Differentialform um eins.
Mit den Differentialformen kann man jetzt rechnen. Man kann sie so handhaben, wie du das später in der Thermodynamik kennenlernen wirst - und man kann sie integrieren (nennt sich dann "Integration über Differentialformen" oder einfacher "Integration auf (diff'baren) Mannigfaltigkeiten"). Das sieht dann etwas anders aus (guck dir den Abschnitt zu den Maxwellgleichungen in Differentialformen bei Wikipedia an). Damit kann man also auch erklären, was das in der Integration soll.
Dein Beispiel ist aber jetzt NOCH mal anders. Die Behandlung z.B. deines Beispiels
 verläuft anders, da es nicht in der Sprache der Differentialgeometrie verfasst. verläuft anders, da es nicht in der Sprache der Differentialgeometrie verfasst.
In der Mathematik fällt das (und Sätze wie der Gaußsche Satz, der Stokessche Satz, etc.) unter den Begriff Vektoranalysis und kann im Rahmen der Mehrdimensionalen Diff- und Int'rechnung wohlbegründet werden. Alleinstehende 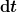 gibt's da aber nicht. gibt's da aber nicht.
Vektoranalysis funktioniert im Endeffekt genauso wie Differentialgeometrie - ist aber in ihrer Handhabung wesentlich komplizierter als die Differentialgeometrie (und weniger allgemein), dafür mit einfacheren Mitteln zugänglich, weil sie nur das Konzept der Ableitung und Integration auf mehrere Dimensionen verallgemeinert.
Zusammenfassung zum  : :
- In der Form  ist's Leibnitzschreibweise für (totale) Ableitung. ist's Leibnitzschreibweise für (totale) Ableitung.
- In der Form  beschreibt es (in der Sprache der Vektoranalysis), worüber integriert wird. Es ist dann ein rein formales Objekt, das man erst einmal in ein "normales" Integral umformt. beschreibt es (in der Sprache der Vektoranalysis), worüber integriert wird. Es ist dann ein rein formales Objekt, das man erst einmal in ein "normales" Integral umformt.
- In derselben Form kann es auch ein Differential sein, dass über eine Mannigfaltigkeit integriert wird. Die Schreibweise ist innerhalb der Physik aber selten verwendet! (insbesondere Jackson verwendet sie NICHT)
- Alleinstehend, z.B. in der Zustandsgleichung beim Gay-Lussac-Versuch:
 ist es ein Differential - in der Physik stellt man sich auch gerne "infinitesimale Größen" vor und hat dann eine "normale Integration" aus der Summe gewonnen. In der Form ergibt die Leibnitzschreibweise Sinn in Form eines Quotienten infinitesimaler Größen. ist es ein Differential - in der Physik stellt man sich auch gerne "infinitesimale Größen" vor und hat dann eine "normale Integration" aus der Summe gewonnen. In der Form ergibt die Leibnitzschreibweise Sinn in Form eines Quotienten infinitesimaler Größen.
Und jetzt zum letzten  . .
Auch dieses  hat - wie könnte es anders sein - verschiedene Bedeutungen. hat - wie könnte es anders sein - verschiedene Bedeutungen.
Einerseits steht es meistens für sogenannte "virtuelle Verrückungen" in der theoretischen Mechanik (siehe d'Alembertsches Prinzip). Das sind auch so infinitesimale Größen, die man zum Beispiel beim Einbau von Zwangsbedingungen benutzt - allerdings gefielen mir die auch nie so richtig...
Andererseits wird  auch gerne für die Funktionalableitung benutzt. In der Variationsrechnung ist es nötig, Funktionen nach sogenannten "Funktionalen" abzuleiten (mit Hilfe der Variationsrechnung werden in der Mechanik die Lagrangegleichungen, die in der Mathematik auch Euler-Lagrangegleichungen heißen, abgeleitet). Das funktioniert so ähnlich wie normale Ableitung und wird manchmal mit dem "normalen" auch gerne für die Funktionalableitung benutzt. In der Variationsrechnung ist es nötig, Funktionen nach sogenannten "Funktionalen" abzuleiten (mit Hilfe der Variationsrechnung werden in der Mechanik die Lagrangegleichungen, die in der Mathematik auch Euler-Lagrangegleichungen heißen, abgeleitet). Das funktioniert so ähnlich wie normale Ableitung und wird manchmal mit dem "normalen"  manchmal - zur Unterscheidung - mit einem manchmal - zur Unterscheidung - mit einem  versehen. Das sieht man z.B. auch im Wiki-Artikel zum Thema "Funktionalableitung". versehen. Das sieht man z.B. auch im Wiki-Artikel zum Thema "Funktionalableitung".
Ganz kurze Zusammenfassung: Wenn man sich also auf den Standpunkt der infinitesimalen Größen bezieht, dann könnte man sagen: Wenn 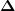 kein Differentialoperator ist, dann gilt: kein Differentialoperator ist, dann gilt:
 ist der Grenzwert von ist der Grenzwert von 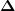 und und  ist ein Synonym für ist ein Synonym für  für spezielle Fälle (Funktionalableitung, virtuelle Verrückungen) - und alles hat etwas mit "Änderungen" bzw. Ableitungen zu tun. für spezielle Fälle (Funktionalableitung, virtuelle Verrückungen) - und alles hat etwas mit "Änderungen" bzw. Ableitungen zu tun.
So - und jetzt stelle ich erschrocken fest, dass ich höchstens ein Viertel hätte schreiben wollen - aber da ich's schon mal geschrieben habe (und doch hoffentlich alles einigermaßen richtig sein sollte  - für Verbesserungen bin ich dankbar!) kann ich's auch posten. Vielleicht nützt es ja was und gibt's jemanden, der das noch anders und wesentlich kürzer zusammenfasst... - für Verbesserungen bin ich dankbar!) kann ich's auch posten. Vielleicht nützt es ja was und gibt's jemanden, der das noch anders und wesentlich kürzer zusammenfasst...
Gruß
MI |
|
 |
die.fly

Anmeldungsdatum: 03.11.2011
Beiträge: 121
|
 die.fly Verfasst am: 24. März 2012 02:34 Titel: die.fly Verfasst am: 24. März 2012 02:34 Titel: |
 |
|
Ok, danke man. hab alles kapiert.
also das mit dem Nablaoperator wusste ich schon. ich meinte die ausgeschreibene form, aber hatte das zeichen falsch geschreiben.
_________________
Physikstudent 2tes Semester |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 24. März 2012 10:07 Titel: MI Verfasst am: 24. März 2012 10:07 Titel: |
 |
|
Ich hatte mir gedacht, dass du den Nabla-Operator in seiner richtigen Form kennst - wollte das nur der Form halber (und falls noch mal jemand hierüber stolpert) erwähnen. Vermutlich wusstest du auch das ein oder andere von dem anderen Kram, den ich geschrieben habe, aber jetzt steht's mal alles zusammen  . .
Gruß
MI |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 30. März 2012 12:11 Titel: franz Verfasst am: 30. März 2012 12:11 Titel: |
 |
|
Noch ein ein Schmankerl: Das waagerecht durchgestrichene / unvollständige Differential (LaTeX so ähnlich  ? neee, oder so ähnlich ? neee, oder so ähnlich 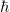 ), bedeutsam in der Thermodynamik. ), bedeutsam in der Thermodynamik.  |
|
 |
|
|
















 - für Verbesserungen bin ich dankbar!) kann ich's auch posten. Vielleicht nützt es ja was und gibt's jemanden, der das noch anders und wesentlich kürzer zusammenfasst...
- für Verbesserungen bin ich dankbar!) kann ich's auch posten. Vielleicht nützt es ja was und gibt's jemanden, der das noch anders und wesentlich kürzer zusammenfasst...
