| Autor |
Nachricht |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 17. Jan 2011 15:06 Titel: DGL aufstellen pippo Verfasst am: 17. Jan 2011 15:06 Titel: DGL aufstellen |
 |
|
Meine Frage:
Hallo,
meine Aufgabe lautet...
Ein Körper der Masse m rutscht mit der Geschwindikeit v in ein Wasserbecken. Dort wird der Körper mit der Kraft F=-bv abgebremst.
a) stellen Sie eine DGL auf, welche den Abbremsvorgang beschreibt.
Mein Problem ist dass wir in unserer Mathevorlesung noch nicht bei den DGL angelangt sind, also ich nur raten kann...
Meine Ideen:
meine Idee wäre sowas:
 |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jan 2011 15:10 Titel: dermarkus Verfasst am: 17. Jan 2011 15:10 Titel: |
 |
|
Wie die Kraft von der Geschwindigkeit v abhängt, ist ja schon gegeben.
Weißt du schon wie eine Beschleunigung a mit der Kraft F zusammenhängt?
Und weißt du vielleicht sogar schon, was eine Beschleunigung mit einer Geschwindigkeit zu tun hat? Was muss man da nach der Zeit ableiten, um das andere zu bekommen?
Kannst du mit solchen Überlegungen zum Beispiel schon eine Gleichung aufstellen, in der als unbekannte Größen nur noch die Funktion v(t) und Ableitungen dieser Funktion v(t) nach der Zeit vorkommen? |
|
 |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 17. Jan 2011 15:28 Titel: pippo Verfasst am: 17. Jan 2011 15:28 Titel: |
 |
|
also die Kraft hängt mit der Beschleunigung über F=ma zusammen;
und die Beschleunigung ist die zeitliche Ableitung der Geschwindigkeit.
so dann versuch ichs nochmal,
der Abbremsvorgang ist ja eine negative Beschleunigung, also die zeitliche Ableitung von v(t) dann müsste die DGL lauten:
 =\frac{ v(t)-b}{m} ) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2011 04:02 Titel: dermarkus Verfasst am: 18. Jan 2011 04:02 Titel: |
 |
|
| pippo hat Folgendes geschrieben: | also die Kraft hängt mit der Beschleunigung über F=ma zusammen;
und die Beschleunigung ist die zeitliche Ableitung der Geschwindigkeit.
|
Einverstanden 
| Zitat: |
der Abbremsvorgang ist ja eine negative Beschleunigung, also die zeitliche Ableitung von v(t) dann müsste die DGL lauten:
 =\frac{ v(t)-b}{m} ) |
Nein, da bist du irgendwie gestolpert, mit diesem Schritt bin ich nicht einverstanden.
Vielleicht magst du lieber erstmal überlegen, ob du laut Aufgabenstellung einfach schon weißt, wie groß das F=m*a sein muss, dann kannst du das nämlich gleich schon mit dem gleichsetzen, was du links mit ) schon stehen hast: schon stehen hast:
 = ???) |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 18. Jan 2011 06:31 Titel: Grundgesetz Systemdynamiker Verfasst am: 18. Jan 2011 06:31 Titel: Grundgesetz |
 |
|
Das Aufstellen der DGL ist die Kernaufgabe der Physik und hat mit Mathematik noch wenig zu tun. In der Mechanik geht das wie folgt:
1. Freischneiden (Kräfte einzeichnen): in der Horizontalen wirkt nur die Reibkraft des Wassers
2. Grundgesetzt (2. Newtonaxiom, Impulsbilanz) aufstellen:
F_1 + F_2 + F_3 +... = dp/dt = m*dv/dt = m*d^2x/dt^2
3. Kraftgesetze ins Grundgesetz einbauen: F_1 = -bv, keine weiteren Kräfte
-b*v = m*dv/dt
Das geht doch wie Lego. Deine Idee war schon richtig, Du hast einfach nur die Lösung hingeschrieben, ohne das Verfahren zu kennen.
_________________
Herzliche Grüsse Werner Maurer |
|
 |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 18. Jan 2011 10:50 Titel: pippo Verfasst am: 18. Jan 2011 10:50 Titel: |
 |
|
Jetzt glaub ich hab ich´s.
Mein Fehler war dass ich links der Gleichung die Beschleunigung hatte, aber da die Kraft hätte stehen müssen... also *m )
und das dann mit der abbremsenden Kraft gleichsetzen...
=\dot{v}(t)*m )
dann dürfte das jetzt so stimmen oder?
Der zweite Aufgabenteil wäre dann:
Lösen Sie die DGL (tipp das geht ganz analog zum Kriechfall des harmonischen gedämpften Oszilators)
In dem Fall habe wir uns eine  Funktion gebastelt und ich denke das dürfte hier wohl auch richtig sein. Funktion gebastelt und ich denke das dürfte hier wohl auch richtig sein.
Mein Ansatz wäre hier dass sich die Kraft mit abnehmender Geschwindigkeit ändert also sowas wie  , mit , mit 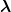 als Reibungskoeffizient. als Reibungskoeffizient.
Stimmt das so? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 18. Jan 2011 11:45 Titel: franz Verfasst am: 18. Jan 2011 11:45 Titel: |
 |
|
| pippo hat Folgendes geschrieben: | =\dot{v}(t)*m ) |
Ohne was gelesen zu haben: Das riecht nach einer Trennung der Variablen (v, t) und dann irgendwie logarithmisch, exponentiell ...  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 18. Jan 2011 14:36 Titel: dermarkus Verfasst am: 18. Jan 2011 14:36 Titel: |
 |
|
| pippo hat Folgendes geschrieben: | Jetzt glaub ich hab ich´s.
Mein Fehler war dass ich links der Gleichung die Beschleunigung hatte, aber da die Kraft hätte stehen müssen... also *m )
und das dann mit der abbremsenden Kraft gleichsetzen...
=\dot{v}(t)*m )
dann dürfte das jetzt so stimmen oder?
|
Einverstanden 
| Zitat: |
Der zweite Aufgabenteil wäre dann:
Lösen Sie die DGL (tipp das geht ganz analog zum Kriechfall des harmonischen gedämpften Oszilators)
In dem Fall habe wir uns eine  Funktion gebastelt und ich denke das dürfte hier wohl auch richtig sein. Funktion gebastelt und ich denke das dürfte hier wohl auch richtig sein.
Mein Ansatz wäre hier dass sich die Kraft mit abnehmender Geschwindigkeit ändert also sowas wie  , mit , mit 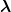 als Reibungskoeffizient. als Reibungskoeffizient.
|
So einen Ansatz hätte auch ich als erstes mal probiert.
Was kommt heraus, wenn du diesen Ansatz versuchst? Passt der Ansatz, und falls ja, was liefert er? |
|
 |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 18. Jan 2011 16:28 Titel: pippo Verfasst am: 18. Jan 2011 16:28 Titel: |
 |
|
ich habs jetzt nochmal überdacht und schlage als Lösung
=-\frac{1}{2} vt^{-2} m )
Denn die Ableitung von 
ist ja  was wiederum die Beschleunigung ist. was wiederum die Beschleunigung ist.
Kanns so stimmen? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 18. Jan 2011 17:42 Titel: franz Verfasst am: 18. Jan 2011 17:42 Titel: |
 |
|
Hallo pippo, mit =\dot{v}(t)*m ) stehst Du dicht an der Lösung. Für welche wichtige Funktion ist die Ableitung gleich der Funktion selber stehst Du dicht an der Lösung. Für welche wichtige Funktion ist die Ableitung gleich der Funktion selber =f(x)) respektiv respektiv \sim v(t)) ? (Das wird doch immer beim Erlernen der Ableitungsregeln hervorgehoben.) Von daher liegt meines Erachtens ein Ansatz für ? (Das wird doch immer beim Erlernen der Ableitungsregeln hervorgehoben.) Von daher liegt meines Erachtens ein Ansatz für ) ganz nahe... ganz nahe...
[Für einen exponentiellen Kraftansatz sehe ich keine Begründung, abgesehen davon, daß die Einheiten nicht stimmen.] |
|
 |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 18. Jan 2011 18:14 Titel: pippo Verfasst am: 18. Jan 2011 18:14 Titel: |
 |
|
Das wäre dann ja wieder di  Funktion oder? Funktion oder? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 18. Jan 2011 18:39 Titel: franz Verfasst am: 18. Jan 2011 18:39 Titel: |
 |
|
| pippo hat Folgendes geschrieben: | Das wäre dann ja wieder di  Funktion oder? Funktion oder? |
 Richtig. Und jetzt übersetzt für das v(t) Problem? Was entspricht dem x? ... Richtig. Und jetzt übersetzt für das v(t) Problem? Was entspricht dem x? ... |
|
 |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 19. Jan 2011 18:42 Titel: pippo Verfasst am: 19. Jan 2011 18:42 Titel: |
 |
|
|
Also da Die Abbremsung von der Geschwindigkeit abhängt und diese von der Zeit, müsste für x entweder v oder t stehen oder? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 19. Jan 2011 18:58 Titel: franz Verfasst am: 19. Jan 2011 18:58 Titel: |
 |
|
Nochmal der Vergleich von oben
=v'(t) \cdot m\rightarrow v'(t)=-\frac{b}{m}v) und und
'=e^x\rightarrow\left(e^{qx}\right)'=q \cdot \left(e^{qx}\right)) |
|
 |
pippo
Anmeldungsdatum: 31.10.2010
Beiträge: 26
|
 pippo Verfasst am: 19. Jan 2011 19:40 Titel: pippo Verfasst am: 19. Jan 2011 19:40 Titel: |
 |
|
Heisst das ich muss eine Funktion finden deren erste Ableitung | franz hat Folgendes geschrieben: |
 |
ist? |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 19. Jan 2011 21:40 Titel: Re: DGL aufstellen franz Verfasst am: 19. Jan 2011 21:40 Titel: Re: DGL aufstellen |
 |
|
Ja, denn
| pippo hat Folgendes geschrieben: | | stellen Sie eine DGL auf, welche den Abbremsvorgang beschreibt. |
... kann man als Frage nach v(t) interpretieren und dazu dient ein, hier schon mehrfach ventilierter, exponentieller Ansatz =p\cdot e^{q\cdot t}) , der (erstmal) zur Ermittlung von q in Deine Gleichung für v(t) , der (erstmal) zur Ermittlung von q in Deine Gleichung für v(t) =\dot{v}(t)*m ) eingesetzt wird. eingesetzt wird. |
|
 |
|

















 Richtig. Und jetzt übersetzt für das v(t) Problem? Was entspricht dem x? ...
Richtig. Und jetzt übersetzt für das v(t) Problem? Was entspricht dem x? ...