| Autor |
Nachricht |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 08. Jun 2015 21:16 Titel: erkü Verfasst am: 08. Jun 2015 21:16 Titel: |
 |
|
Hallo,
stell erst mal die Maschengleichung für die drei zeitabhängigen Spannungen auf.
Dann sehen wir weiter. 
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 08. Jun 2015 23:25 Titel: erkü Verfasst am: 08. Jun 2015 23:25 Titel: |
 |
|
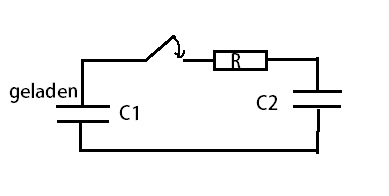
Der Maschenumlauf bei geschlossenem Schalter ergibt:
+U_R(t)+U_{C_2}(t)=0)
Wie willst Du hier eine DGL aufstellen ?
Also wird der (alleinige) Strom ) eingeführt. eingeführt.
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 09. Jun 2015 18:07 Titel: Max Cohen Verfasst am: 09. Jun 2015 18:07 Titel: |
 |
|
Hallo erkü, so ganz sehe ich nicht wie mich das nun weiter bringt. Die Spannung in den Kondensatoren müsste ich erhalten indem ich berechne =\frac{1}{C}\int i(t)dt) . Für die Spannung des Widerstandes kann ich ja . Für die Spannung des Widerstandes kann ich ja 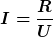 setzen. setzen.
Wie soll ich das denn nun berechnen?
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 09. Jun 2015 18:50 Titel: erkü Verfasst am: 09. Jun 2015 18:50 Titel: |
 |
|
| erkü hat Folgendes geschrieben: | Der Maschenumlauf bei geschlossenem Schalter ergibt:
+U_R(t)+U_{C_2}(t)=0)
Wie willst Du hier eine DGL aufstellen ?
Also wird der (alleinige) Strom ) eingeführt. eingeführt. |
Und dann obige Gleichung nach der Zeit t abgeleitet.
Das ergibt eine DGL in ) ! !
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 09. Jun 2015 19:26 Titel: Max Cohen Verfasst am: 09. Jun 2015 19:26 Titel: |
 |
|
Mit  und und  erhalte ich dann: erhalte ich dann:




=-\int \frac{1}{C}[i_1+i_2]dt)
Meinst du das so?
Gruß
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 09. Jun 2015 22:02 Titel: GvC Verfasst am: 09. Jun 2015 22:02 Titel: |
 |
|
| erkü hat Folgendes geschrieben: | Der Maschenumlauf bei geschlossenem Schalter ergibt:
+U_R(t)+U_{C_2}(t)=0)
... |
Das ist nicht ganz richtig. Richtig wäre
+U_R(t)+U_{C_2}(t)=0)
Allerdings musst Du dann auch berücksichtigen, dass wegen entgegengesetzter Richtung von Spannung und Strom an C1 gilt
=-\frac{1}{C_1}\int i(t)\, dt)
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 09. Jun 2015 22:11 Titel: GvC Verfasst am: 09. Jun 2015 22:11 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Mit  und und  erhalte ich dann: erhalte ich dann:


... |
Da geht ja Einiges bei Dir durcheinander. Das stimmt ja schon dimensionsmäßig nicht. Dabei hattest Du schon den richtigen Ansatz. Du wolltest die Spannungen an den Kondensatoren ersetzen durch
=\frac{1}{C}\int i(t)\, dt)
Warum machst Du das nicht?
\, dt+R\cdot i(t)+\frac{1}{C_2}\int i(t)\, dt)
Ableitung nach der Zeit ergibt
\cdot i(t)+R\cdot\frac{di(t)}{dt}=0)
Kommst Du jetzt weiter?
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 10. Jun 2015 14:25 Titel: Max Cohen Verfasst am: 10. Jun 2015 14:25 Titel: |
 |
|
Hi GvC, damit komme ich jetzt zurecht. Ich trottel habe das ohmsche Gesetz nach i aufgelöst und dann eingesetzt und nicht U=Ri eingesetzt. Dann komme ich auf deine besagte DGL. Die DGL lässt sich mittels Seperation lösen. Ich komme dann auf:
=i_0e^{-\frac{1}{R}(\frac{1}{C_1}+\frac{1}{C_2})t})
Da laut Aufgabenstellung die Kapazitäten in beiden Kondensatoren Gleich sind kann ich  setzen und komme dann auf: setzen und komme dann auf:
=i_0e^{-\frac{2}{RC}t})
Da nach den Spannungen in den jeweiligen Kondensator gefragt ist muss ich nun das Integral =\frac{1}{C}\int_0^{\infty} i_0e^{-\frac{2}{RC}t}dt) lösen mit den Integrationsgrenzen 0 und Unendlich da laut Aufgabenstellung der Kondensator den stationären Zustand erreicht hat. Ich denke da wählt man als Integrationsgrenze Unendlich? lösen mit den Integrationsgrenzen 0 und Unendlich da laut Aufgabenstellung der Kondensator den stationären Zustand erreicht hat. Ich denke da wählt man als Integrationsgrenze Unendlich?
Falls ja komme ich auf:

=\frac{1}{2}Ri_0)
Und das gilt dann für beide Kondensatoren.
Ist das soweit richtig?
Danke euch beiden!
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 10. Jun 2015 15:17 Titel: GvC Verfasst am: 10. Jun 2015 15:17 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Hi GvC, damit komme ich jetzt zurecht. Ich trottel habe das ohmsche Gesetz nach i aufgelöst und dann eingesetzt und nicht U=Ri eingesetzt. Dann komme ich auf deine besagte DGL. Die DGL lässt sich mittels Seperation lösen. Ich komme dann auf:
=i_0e^{-\frac{1}{R}(\frac{1}{C_1}+\frac{1}{C_2})t})
Da laut Aufgabenstellung die Kapazitäten in beiden Kondensatoren Gleich sind kann ich  setzen und komme dann auf: setzen und komme dann auf:
=i_0e^{-\frac{2}{RC}t}) |
Nun musst Du nur noch bestimmen, wie groß  ist. Außerdem würde ich, um im Folgenden Schreibarbeit zu sparen, die Zeitkonstante einführen: ist. Außerdem würde ich, um im Folgenden Schreibarbeit zu sparen, die Zeitkonstante einführen:

| Max Cohen hat Folgendes geschrieben: | Da nach den Spannungen in den jeweiligen Kondensator gefragt ist muss ich nun das Integral =\frac{1}{C}\int_0^{\infty} i_0e^{-\frac{2}{RC}t}dt) lösen mit den Integrationsgrenzen 0 und Unendlich da laut Aufgabenstellung der Kondensator den stationären Zustand erreicht hat. lösen mit den Integrationsgrenzen 0 und Unendlich da laut Aufgabenstellung der Kondensator den stationären Zustand erreicht hat. |
Nein, das steht da nicht. Im Gegenteil, laut der von Dir vorgelegten Aufgabenstellung ist nach dem zeitlichen Verlauf der Spannung an den beiden Kondensatoren gefragt.
| Max Cohen hat Folgendes geschrieben: | | Ich denke da wählt man als Integrationsgrenze Unendlich? |
Wie gesagt, nein.
| Max Cohen hat Folgendes geschrieben: | Falls ja komme ich auf:

=\frac{1}{2}Ri_0)
Und das gilt dann für beide Kondensatoren.
Ist das soweit richtig? |
Nein, das wäre nur richtig für den Endwert der beiden Spannungen, Allerdings müsste der Anfangsstrom noch durch die gegebenen Größen ausgedrückt werden.
Der zeitliche Verlauf der beiden Spannungen ist übrigens unterschiedlich. Der linke Kondensator entlädt sich, während der rechte aufgeladen wird.
Der Spannungsverlauf errechnet sich allgemein aus
=\frac{1}{C}\int i(t)\, dt)
Denke daran, dass es sich um ein unbestimmtes Integral handelt, welches noch eine additive Konstante enthält (Integrationskonstante), die Du aus der jeweiligen Anfangsbedingung bestimmen kannst.
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 10. Jun 2015 15:42 Titel: Max Cohen Verfasst am: 10. Jun 2015 15:42 Titel: |
 |
|
Also ich denke man kann die Anfangsbedingung =0) wählen? Dann komme ich auf wählen? Dann komme ich auf  und erhalte dann: und erhalte dann:
=e^{-\frac{2RC}t})
Nun muss der Spannungsverlauf in den beiden Kondensatoren bestimmt werden mit der Formel =\frac{1}{C}\int i(t)dt)
Wenn es keine Integrationsgrenzen gibt dann macht das auch keinen Sinn meine Lösung. Wenn ich dies einmal integriere erhalte ich:
=\frac{1}{C}\int i(t)dt=\frac{1}{C}\int e^{-\frac{2RC}t}dt=-\frac{1}{2}Re^{-\frac{2}{RC}t}+k)
Nun kommt es auf den jeweiligen Kondensator an der betrachtet wird. Das heißt beide besitzen unterschiedliche Anfangsbedingungen. Da zweite Kondensator muss die Anfangsbedingung =0) besitzen und der erste weiß ich ehrlich gesagt nicht. besitzen und der erste weiß ich ehrlich gesagt nicht.
Muss ich dazu noch eine weitere Rechnung durchführen oder nur scharf hinschauen?
Danke dir!
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 10. Jun 2015 22:39 Titel: erkü Verfasst am: 10. Jun 2015 22:39 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Also ich denke man kann die Anfangsbedingung =0) wählen? Dann komme ich auf wählen? Dann komme ich auf  und erhalte dann: und erhalte dann:
=e^{-\frac{2RC}t})
...
|
Links Strom, rechts dimensionslose Zahl (und auch noch verkehrt) ! 
Oh man, das ist alles für's 
1. Der Exponent muss lauten 
2. Die Lösung der DGL ergibt =c\cdot e^{-t/\tau})
3. Anfangsbedingung =\frac{U_0}{R}=c) (Ein ungeladener Kondensator stellt einen Kurzschluss dar !) (Ein ungeladener Kondensator stellt einen Kurzschluss dar !)
4. =-\frac{1}{C_1}\int\frac{U_0}{R}\,e^{-t/\tau}\,\mathrm dt)
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk:
Zuletzt bearbeitet von erkü am 11. Jun 2015 02:07, insgesamt 3-mal bearbeitet |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 10. Jun 2015 23:03 Titel: Max Cohen Verfasst am: 10. Jun 2015 23:03 Titel: |
 |
|
Hallo erkü, ich sehe es gerade selber das ich mich verschrieben habe. In meinen Beiträgen zuvor hätte das eigentlich auffallen müssen da ich den Strom i korreckt angegeben habe.
Mit der Anfangsbedingung lautet dann der Strom =\frac{U_0}{R}e^{-\frac{2}{RC}t})
=-\frac{1}{C}\frac{U_1}{R}\int e^{-\frac{2}{RC}t}=\frac{1}{C}\frac{U_0}{R}\frac{RC}{2}e^{-\frac{2}{RC}t}+k=\frac{1}{2}U_0e^{-\frac{2}{RC}t}+k)
Damit habe ich dann =\frac{1}{2}U_0e^{-\frac{2}{RC}t}+k)
Für den Kondensator 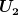 erhält man dann den selben Ausdruck bloß mit einem Minuszeichen. erhält man dann den selben Ausdruck bloß mit einem Minuszeichen.
=-\frac{1}{2}U_0e^{-\frac{2}{RC}t}+g)
Nun fehlen noch die Konstanten k und g. Dazu muss ich die Anfangsbedingungen wissen also ) und und ) . Wie erhalte ich die oder was gilt in dem Fall? . Wie erhalte ich die oder was gilt in dem Fall?
Danke!
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 11. Jun 2015 09:40 Titel: GvC Verfasst am: 11. Jun 2015 09:40 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | ...
Für den Kondensator 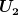 erhält man dann den selben Ausdruck bloß mit einem Minuszeichen. erhält man dann den selben Ausdruck bloß mit einem Minuszeichen.
=-\frac{1}{2}U_0e^{-\frac{2}{RC}t}+g) |
Nein. Weshalb Minuszeichen? Beim rechten Kondensator sind doch Strom und Spannung nicht entgegengesetzt gerichtet, oder?
| Max Cohen hat Folgendes geschrieben: | Nun fehlen noch die Konstanten k und g. Dazu muss ich die Anfangsbedingungen wissen also ) und und ) . Wie erhalte ich die oder was gilt in dem Fall? . Wie erhalte ich die oder was gilt in dem Fall?
|
Denke daran, dass die Spannung am Kondensator sich nicht sprunghaft ändern kann. Also:
1. Wie groß ist die Spannung am linken Kondensator unmittelbar vor dem Schalten? (Die Antwort auf diese Frage hast Du bereits bei der Bestimmung des Anfangsstromes verwendet.)
2. Wie groß ist die Spannung am rechten Kondensator unmittelbar vor dem Schalten?
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Jun 2015 21:32 Titel: Max Cohen Verfasst am: 11. Jun 2015 21:32 Titel: |
 |
|
Hallo GvC, ich dachte das Minuszeichen bei 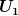 kam dadurch zustande da du in deinem ersten Beitrag geschrieben hast das kam dadurch zustande da du in deinem ersten Beitrag geschrieben hast das  gilt. Für gilt. Für 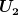 hast du geschrieben das hast du geschrieben das 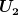 positiv ist. Deshalb dachte ich kommen unterschiedliche Vorzeichen zustande. Scheint aber nicht so zu sein. Woher kommt dann das Vorzeichen für positiv ist. Deshalb dachte ich kommen unterschiedliche Vorzeichen zustande. Scheint aber nicht so zu sein. Woher kommt dann das Vorzeichen für 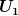 ? ?
Das heißt dann also das
=\frac{1}{2}U_0e^{-\frac{2}{RC}t}+g) und und
=\frac{1}{2}U_0e^{-\frac{2}{RC}t}+k) gilt. gilt.
Jetzt zu der Bestimmung der Anfangsbedingungen.
Zum de linken Kondensator: Hier habe ich mit dem ohmschen Gesetz den Anfangsstrom bestimmt ich denke dann gilt =Ri)
Im rechten Kondensator ist die Spannung =0) da der Schalter noch nicht umgelegt wurde da der Schalter noch nicht umgelegt wurde
Ich denke das macht Sinn. 
Danke
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 12. Jun 2015 01:24 Titel: GvC Verfasst am: 12. Jun 2015 01:24 Titel: |
 |
|
@Max Cohen
Beim Vorzeichen von U2 habe ich mich vertan. Ich hatte Deine Integrationskonstante g übersehen (avber selbst dann hätte ich falsch gelegen, sorry).
Wieso schreibst Du für die Anfangsspannung des linken Kondensators R*i? Das ist zwar nicht ganz falsch, aber eigentlich orientiert man sich bei der Anfangsspannung eines Kondensators an seiner Spannung unmittelbar vor dem Schalten. Der Strom i fließt aber erst nach dem Schalten.
Noch einmal der ganz wesentliche Merksatz: Die Spannung an einem Kondensator kann sich nicht sprunghaft ändern.
Einen ähnlichen Satz gibt es für die Induktivität (in dieser Aufgabe nicht relevant, da es keine Induktivität gibt): Der Strom durch eine Induktivität kann sich nicht sprunghaft ändern.
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 12. Jun 2015 16:24 Titel: Max Cohen Verfasst am: 12. Jun 2015 16:24 Titel: |
 |
|
Hallo ihr beiden, also die Anfangsbedingung für den zweiten Kondensator passt also?
Es erscheint mir erstmal logisch da der erste Kondensator von 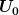 vor dem Schalten aufgeladen wird. Die Frage die sich mir allerdings stellt, wie lange wird dieser aufgeladen. Bis der Kondensator voll geladen ist und dann wird geschaltet? Falls dem so ist dann besitzt vor dem Schalten aufgeladen wird. Die Frage die sich mir allerdings stellt, wie lange wird dieser aufgeladen. Bis der Kondensator voll geladen ist und dann wird geschaltet? Falls dem so ist dann besitzt 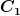 die selbe Ladung wie die selbe Ladung wie 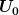 . Also die Ladung . Also die Ladung 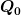 und dieser besitzt die Kapazität und dieser besitzt die Kapazität  Mit Mit  gilt dann gilt dann  Jetzt mal ohne Einheiten. Jetzt mal ohne Einheiten.
Wie ist das denn definiert, also wann sagt man der Schalter wird umgelegt. Wenn der erste Kondensator voll geladen ist?
Das die Spannung an einem Kondensator keine Sprünge macht sagt dann ja quasi das der Aufladevorgang des Kondensators nicht infinitesimal klein ist sondern das eine gewisse Zeit dafür benötigt wird.
Danke!
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Jun 2015 12:36 Titel: Max Cohen Verfasst am: 13. Jun 2015 12:36 Titel: |
 |
|
Hat noch jemand eine Idee?
Zum Teil b) dachte ich nun die Leistung zu integrieren. Es gilt hier  und und ) und und ) habe ich im Teil a) bestimmt. habe ich im Teil a) bestimmt.
Dann gilt nämlich U(t)dt=\int\frac{U_0}{R}e^{-\frac{2}{RC}t}\cdot\frac{U_0}{2}e^{-\frac{2}{RC}t}dt=\frac{U_0^2}{2R}\int e^{-\frac{4}{RC}t}dt)
Für den zweiten Fall müssten die Grenzen von  gehen. Bei dem ersten Fall bin ich mir nicht sicher aber den müsste ich wohl mit einem Grenzwert betrachten indem ich gehen. Bei dem ersten Fall bin ich mir nicht sicher aber den müsste ich wohl mit einem Grenzwert betrachten indem ich  laufen lasse. Dann erhält man laufen lasse. Dann erhält man  . .
Ich habe auch noch garnicht die Anfangsbedingung für die Spannung eingesetzt. Eventuell vereinfacht sich das ganze auch noch ... ?
Danke!
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 13. Jun 2015 14:13 Titel: GvC Verfasst am: 13. Jun 2015 14:13 Titel: |
 |
|
Ich weiß gar nicht, was Du immer mit der Ladung hast. Laut Aufgabenstellung ist der linke Kondensator auf die Spannung U0 aufgeladen, basta. Mehr brauchst Du doch gar nicht zu wissen. Die Spannung vor dem Schalten ist also U0. Da die Spannung am Kondensator wegen
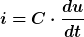
sich nicht sprunghaft ändern kann (das würde nämlich nach dieser Gleichung einen unendlich hohen Strom erfordern, den es realistischerweise nicht gibt), ist die Spannung des linken Kondensators unmittelbar nach dem Schalten eben U0, während die des rechten Kondensators null ist. Aus diesen Anfangsbedingungen lassen sich die Integrationskonstanten, die Du k und g genannt hast, sofort bestimmen.
| Max Cohen hat Folgendes geschrieben: | | Das die Spannung an einem Kondensator keine Sprünge macht sagt dann ja quasi das der Aufladevorgang des Kondensators nicht infinitesimal klein ist sondern das eine gewisse Zeit dafür benötigt wird. |
So ist es. Das drückt sich in der nach u aufgelösten obigen Gleichung aus:

| Max Cohen hat Folgendes geschrieben: | | Zum Teil b) dachte ich nun die Leistung zu integrieren. |
Das kannst Du zwar machen, aber wenn Du das tust, dann solltest Du es richtig machen. Warum verwendest Du nicht einfach die allgemeine Formel für einen auf die Spannung U aufgeladenen Kondensator?
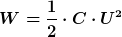
Zu Beginn der Umladung ist die gesamte Energie im ersten (linken) Kondensator gespeichert, ist also

Nach der Umladung haben beide Kondensatoren die Spannung U2, die Du noch bestimmen musst. Da beide Kondensatoren dieselbe Kapazität haben, ist dann die in beiden Kondensatoren gespeicherte Energie

und ist verblüffenderweise kleiner als die Anfangsenergie, was dem Energieergaltungssatz zu widersprechen scheint. Kannst Du Dir vorstellen, wo die fehlende Energie gebleiben ist?
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Jun 2015 15:02 Titel: Max Cohen Verfasst am: 13. Jun 2015 15:02 Titel: |
 |
|
Ok, dann gilt für den ersten Kondensator also =U_0)
mit =\frac{1}{2}U_0e^{-\frac{2}{RC}t}+k) gilt dann: gilt dann:
=U_0=\frac{1}{2}U_0e^{-\frac{2}{RC}t}+k) damit ist damit ist
 Eingesetzt erhalte ich dann... Eingesetzt erhalte ich dann...
=U_0)
Für den zweiten kondensator gilt dann: =0 )
=0=\frac{1}{2}U_0e^{-\frac{2}{RC}t}+g)

Damit lautet =\frac{1}{2}U_0e^{-\frac{2}{RC}t}-\frac{1}{2}U_0e^{-\frac{2}{RC}t}=0)
Passt das jetzt?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 13. Jun 2015 15:26 Titel: GvC Verfasst am: 13. Jun 2015 15:26 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | | Passt das jetzt? |
Nein, das passt ganz und gar nicht.
Für den linken Kondensator hast Du die Anfangsbedingung U1(0)=U0 eingesetzt und erhältst als Ergebnis U1(0)= U0. Was soll das denn? Du drehst Dich im Kreise. Du willst doch nicht U1(0) bestimmen, das kennst Du ja schon, das hast Du ja vorgegeben. Was Du bestimmen willst, ist doch der zeitliche Verlauf U1(t), oder?
Beim rechten Kondensator kommt bei Dir als Ergebnis des zeitlichen Verlaufs eine Konstante heraus, nämlich U2(t)=0. Das kann nicht sein. Wir hatten doch bereits festgestellt, dass der linke Kondensator sich entlädt, während der rechte sich auflädt. Und diesen Entlade- bzw. Aufladevorgang willst Du doch bestimmen.
Tipp: Wenn Du U1(0) bzw. U2(0) einsetzt, musst Du in Deiner allgemeinen Lösung überall dort, wo die Zeit t auftaucht, natürlich t=0 einsetzen. Daraus berechnest Du dann die Integrationskonstanten k bzw. g (bei Dir sind die Konstanten komischerweise zeitlich abhängig), und setzt die dann in die allgemeine Lösungsformel ein.
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Jun 2015 16:05 Titel: Max Cohen Verfasst am: 13. Jun 2015 16:05 Titel: |
 |
|
So, jetzt nochmal langsam.
Ich soll ) einsetzen gilt dann auch einsetzen gilt dann auch =U_0) oder was ist das dann? oder was ist das dann?
=U_0=\frac{1}{2}U_0+k) dann ist dann ist 
Also =\frac{1}{2}U_0e^{-\frac{2}{RC}t}+\frac{1}{2}U_0)
Für =0 )
 dann ist dann ist 
Jetzt muss es aber passen. Dieses mal sind es zumindest Konstanten.
Gruß
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 13. Jun 2015 17:00 Titel: GvC Verfasst am: 13. Jun 2015 17:00 Titel: |
 |
|
Wenn Du jetzt bei U1(t) noch ein bisschen zusammenfasst, dann ist U1(t) schon mal richtig.
Bei U2(t) hast Du das Minuszeichen vergessen. Die allgemeine Lösug lautet ja
=-\frac{1}{2}U_0\cdot e^{-\frac{t}{\tau}}+g)
Dann ist

Das setzt Du in die allgemeine Lösung ein (das hast Du bislang noch micht gemacht).
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Jun 2015 18:15 Titel: Max Cohen Verfasst am: 13. Jun 2015 18:15 Titel: |
 |
|
Ich erhalte dann für die Spannungen
=\frac{1}{2}U_0[e^{-\frac{2}{RC}t}+1] )
=-\frac{1}{2}U_0[e^{-\frac{2}{RC}t}-1])
Jetzt zu der b)
Da hast du ja schon die Antwort gegeben mit  für die Energie im linken Kondensator und für die Energie im linken Kondensator und 
Ich denke die fehlende Energie ist in Reibung über gegangen da sich z.B. zwischen den Kondensatorplatten ein Medium befindet?
Soweit Danke!
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 13. Jun 2015 18:41 Titel: GvC Verfasst am: 13. Jun 2015 18:41 Titel: |
 |
|
Ich hätte das ja so geschrieben:
=\frac{1}{2}U_0\cdot (1+e^{-\frac{t}{\tau}}) )
=\frac{1}{2}U_0\cdot (1-e^{-\frac{t}{\tau}}) )
Dann hat man die Spannungsverläufe gleich vor Augen.
| Max Cohen hat Folgendes geschrieben: | Jetzt zu der b)
Da hast du ja schon die Antwort gegeben mit  für die Energie im linken Kondensator und für die Energie im linken Kondensator und  |
Wie groß ist denn U2? Wie groß ist also W2? Man will das doch mit der Anfangsenergie vergleichen. Wieviel Energie ist also verloren gegangen?
| Max Cohen hat Folgendes geschrieben: | | Ich denke die fehlende Energie ist in Reibung über gegangen da sich z.B. zwischen den Kondensatorplatten ein Medium befindet? |
Bei den Kondensatoren handelt es sich um ideale Elemente. Da fließt kein ladungsträgergebundener Strom durch, nur ein sog. Verschiebungsstrom. Der macht keine Verluste. Aber der Ladungsträgerstrom fließt ja durch den Widerstand R und macht dort Verluste. Die "fehlende" Energie wird im Widerstand in Wärmeenergie ungewandelt.
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Jun 2015 20:12 Titel: Max Cohen Verfasst am: 13. Jun 2015 20:12 Titel: |
 |
|
Für die Energie  Also Also  und und 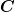 ist bekannt allerdings ist bekannt allerdings 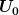 ist in der Aufgabe nicht bekannt. Soll man hier den Grenzwert betrachten mit ist in der Aufgabe nicht bekannt. Soll man hier den Grenzwert betrachten mit 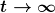 ? ?
Sonst hätte ich jetzt auch keinen Ansatz ...
Danke!
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 05. Jul 2015 12:28 Titel: Max Cohen Verfasst am: 05. Jul 2015 12:28 Titel: |
 |
|
Ich muss den Thread noochmal ausgraben da mich immer noch eine Frage beschäftigt und zwar wenn der Schalter umgelegt wird gilt die DGL 
Der erste Einwand von GvC war das ein Minus vor  stehen muss was doch laut Maschensatz auch richtig auch schon aufgrund Energieerhaltung? stehen muss was doch laut Maschensatz auch richtig auch schon aufgrund Energieerhaltung?
Warum muss hier ein Plus stehen?
Danke schonmal
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 07. Jul 2015 18:32 Titel: GvC Verfasst am: 07. Jul 2015 18:32 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | | Warum muss hier ein Plus stehen? |
Weil Spannung und Strom beim sich entladenden Kondensator einander entgegengerichtet sind.
Im Übrigen bist Du ja immer noch mit der Ladung zugange. Warum? Das ist zwar nicht grundsätzlich falsch, aber es ist doch ausschließlich nach den Spannungen und dem Strom gefragt. Also stellst Du den Maschensatz auf

und setzt die Beziehung zwischen Spannung und Strom an einer Kapazität ein, nämlich

Wegen der oben erwähnten Richtungsbesonderheit an C1 gilt dann
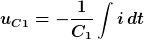
und
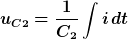
Damit ergibt sich der Maschensatz zu

usw.
Da
)
könnte man natürlich, ähnlich wie Du, schreiben
}{C1}+i\cdot R+\frac{q_2(t)}{C_2}=0)
aber wozu? Es ist doch nach dem Strom gefragt!
|
|
 |
|