| Autor |
Nachricht |
m11lk
Gast
|
 m11lk Verfasst am: 13. Mai 2009 18:55 Titel: DGL gedämpfte Schwingungen m11lk Verfasst am: 13. Mai 2009 18:55 Titel: DGL gedämpfte Schwingungen |
 |
|
Hallo
Ich hab da eine Frage:
Ich habe folgende DGL:
+k\dot y(t)+Dy(t)=0)
Kann ich das nach ) umstellen? umstellen?
Ich habe schon probiert:
)
sowie deren Ableitungen einzusetzen und nach 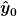 umzustellen. Aber da kommt dann umzustellen. Aber da kommt dann 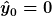 raus. (Ich folgere daraus mein Ansatz ist falsch) raus. (Ich folgere daraus mein Ansatz ist falsch)
Ich bin jetzt beim Suchen nach anderen Ansätzen u.a. auf folgende Seite gestoßen:
matheboard.de/archive/289488/thread.html
Der Treadstarter wird u.a. auf math.tu-berlin.de/geometrie/Lehre/WS03/AuG_inf/vl10.all.pdf verwiesen.
Leider verstehe ich das nicht.

könnt ihr mir vielleicht noch sagen warum mein Lösungsansatz nicht funktioniert hat?
Und: Ich kenne mich nicht mit Differentalgleichungen aus... 
Ach ich hab gerade das bei euch gefunden...
physikerboard.de/topic,13589,-dgl-harmonischer-oszillator.html |
|
 |
bottom

Anmeldungsdatum: 04.02.2009
Beiträge: 333
Wohnort: Kiel
|
 bottom Verfasst am: 13. Mai 2009 20:25 Titel: Re: DGL gedämpfte Schwingungen bottom Verfasst am: 13. Mai 2009 20:25 Titel: Re: DGL gedämpfte Schwingungen |
 |
|
erstmal hallo und ein lob an dich dass du schon selbst recherchiert hast, bevor du einfach fragst! ist heutzutage leider nichtmehr selbstverständlich 
| m11lk hat Folgendes geschrieben: | Ich habe folgende DGL:
+k\dot y(t)+Dy(t)=0)
Kann ich das nach ) umstellen? umstellen?
|
umstellen im sinne von termunformungen geht nicht. was du willst, ist die dgl lösen
| m11lk hat Folgendes geschrieben: | Ich habe schon probiert:
)
sowie deren Ableitungen einzusetzen und nach 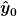 umzustellen. Aber da kommt dann umzustellen. Aber da kommt dann 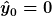 raus. (Ich folgere daraus mein Ansatz ist falsch) raus. (Ich folgere daraus mein Ansatz ist falsch)
[...]
könnt ihr mir vielleicht noch sagen warum mein Lösungsansatz nicht funktioniert hat?
|
bist du sicher, dass 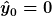 raus kommt? hab dass jetzt nicht nachgerechnet, aber auf den ersten blick würde ich behaupten, dass sich raus kommt? hab dass jetzt nicht nachgerechnet, aber auf den ersten blick würde ich behaupten, dass sich 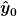 rauskürzen müsste. rauskürzen müsste.
dein Lösungsansatz kann aber so auch nicht funktionieren, da es sich dabei sozuagen um einen teil der entgültigen lösung handelt, sozusagen eine vereinfachte lösung. so schlecht war deine idee aber auch nicht 
du sagst du kennst dich (noch) nicht mit dgl's aus. wenn du deine lösen möchtest, musst du da wohl oder übel ein wenig zu lernen 
ich nur kurz versuchen den ansatz zu erklären, wenn du wirklich verstehen möchtest warum mann das so machen kann, musst du dich näher damit auseinandersetzen. folgendes ist also mehr eine art "kochrezept" nach dem du in deinem fall vorgehen kannst.
Bei deiner DGL handelt es sich um eine lineare, homogene dgl zweiten Grades. der ansatz den du zur lösung brauchst ist der sogenannte exponentialansatz. du sagst einfach =c\cdot e^{\lambda t}) . Mit dieser gleichung machst du dann genau dass was du schon probiert hast: du setzt sie (und die ableitungen) in die dgl ein. . Mit dieser gleichung machst du dann genau dass was du schon probiert hast: du setzt sie (und die ableitungen) in die dgl ein.
Daraus bekommst du dann eine quadratische Gleichung mit  als variablen (das ist die sogenannte Charakteristische Gleichung). wenn du sie löst erhälst du 2 lösungen: als variablen (das ist die sogenannte Charakteristische Gleichung). wenn du sie löst erhälst du 2 lösungen: 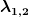 . Diese Beiden Lösungen werden als Fundamentalsystem bezeichnet. . Diese Beiden Lösungen werden als Fundamentalsystem bezeichnet.
=c_1 \cdot e^{\lambda_1 t})
=c_2 \cdot e^{\lambda_2 t})
Die sogennante Linearkombination dieser beiden speziellen Lösungen ergibt dann die allgemeine Lösung:
=c_1 \cdot e^{\lambda_1 t}+c_1 \cdot e^{\lambda_2 t})
hierbei handelt es sich um die allgemeine Lösung der dgl. Diese beinhaltet unterschiedliche Fälle (für unterschiedliche starke Dämpfung). Du bist warsch interessiert an der lösung für die schwache dämpfung (die gleichung die du schon oben genannt hast).
versuch doch mal dass soweit nachvollzuziehen, dann kann ich dir noch zeigen wie man von da zum speziellen fall der schwachen dämpfung kommt.
gruß bottom
_________________
Zuletzt bearbeitet von bottom am 13. Mai 2009 23:28, insgesamt einmal bearbeitet |
|
 |
m12lk
Gast
|
 m12lk Verfasst am: 13. Mai 2009 23:00 Titel: Re: DGL gedämpfte Schwingungen m12lk Verfasst am: 13. Mai 2009 23:00 Titel: Re: DGL gedämpfte Schwingungen |
 |
|
| bottom hat Folgendes geschrieben: | erstmal hallo und ein lob an dich dass du schon selbst recherchiert hast, bevor du einfach fragst! ist heutzutage leider nichtmehr selbstverständlich 
|
Ich hab sogar ein paar Lehrer genervt, die mir aber nicht direckt weiter helfen konnten.
| bottom hat Folgendes geschrieben: |
| m11lk hat Folgendes geschrieben: | Ich habe folgende DGL:
+k\dot y(t)+Dy(t)=0)
Kann ich das nach ) umstellen? umstellen?
|
umstellen im sinne von termunformungen geht nicht. was du willst, ist die dgl lösen
| m11lk hat Folgendes geschrieben: | Ich habe schon probiert:
)
sowie deren Ableitungen einzusetzen und nach 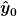 umzustellen. Aber da kommt dann umzustellen. Aber da kommt dann 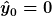 raus. (Ich folgere daraus mein Ansatz ist falsch) raus. (Ich folgere daraus mein Ansatz ist falsch)
[...]
könnt ihr mir vielleicht noch sagen warum mein Lösungsansatz nicht funktioniert hat?
|
bist du sicher, dass 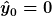 raus kommt? hab dass jetzt nicht nachgerechnet, aber auf den ersten blick würde ich behaupten, dass sich raus kommt? hab dass jetzt nicht nachgerechnet, aber auf den ersten blick würde ich behaupten, dass sich 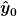 rauskürzen müsste. rauskürzen müsste.
dein Lösungsansatz kann aber so auch nicht funktionieren, da es sich dabei sozuagen um einen teil der entgültigen lösung handelt, sozusagen eine vereinfachte lösung. so schlecht war deine idee aber auch nicht 
|
Ja ich bin mir sicher. Bei den Ableitungen kann ich ja 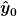 einfach ausklammern (muss ich ja nicht ableiten). Dann erhalte ich nach dem einsetzen einfach einfach ausklammern (muss ich ja nicht ableiten). Dann erhalte ich nach dem einsetzen einfach 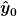 mal den Rest gleich null. Ja und dann passiert das was ich beschrieben habe. (Ich hoffe das war ausführlich genug, ick kann sonst gerne nen ooo Dokument dir Zeigen mal den Rest gleich null. Ja und dann passiert das was ich beschrieben habe. (Ich hoffe das war ausführlich genug, ick kann sonst gerne nen ooo Dokument dir Zeigen  ) )
Sorry die Erklärung warum das nicht geht hab ich nicht verstanden 
| bottom hat Folgendes geschrieben: |
du sagst du kennst dich (noch) nicht mit dgl's aus. wenn du deine lösen möchtest, musst du da wohl oder übel ein wenig zu lernen 
|
Damit hab ich kein Problem. Morgen ist schon mein Weg zur Bückerei geplant... Das Dumme ist, mir fehlen fast alle Grundlagen (bin erst 12.)
| bottom hat Folgendes geschrieben: |
ich nur kurz versuchen den ansatz zu erklären, wenn du wirklich verstehen möchtest warum mann das so machen kann, musst du dich näher damit auseinandersetzen. folgendes ist also mehr eine art "kochrezept" nach dem du in deinem fall vorgehen kannst.
|
Kochrezept... Hmm ich koch normalerweise nur dann wenn ich das Nachvollziehen kann...
| bottom hat Folgendes geschrieben: |
Bei deiner DGL handelt es sich um eine lineare, homogene dgl zweiten Grades. der ansatz den du zur lösung brauchst ist der sogenannte exponentialansatz. du sagst einfach =c\cdot e^(\lambda t)) . .
|
*Stop* wo kommt dieser Ansatz her?! und das soll doch =c\cdot e^{(\lambda t)}) heißen oder? heißen oder?
Ist das  da die Wellenlänge und das da die Wellenlänge und das  die Ausbreitungsgeschwindigkeit? die Ausbreitungsgeschwindigkeit?
| bottom hat Folgendes geschrieben: |
Mit dieser gleichung machst du dann genau dass was du schon probiert hast: du setzt sie (und die ableitungen) in die dgl ein.
Daraus bekommst du dann eine quadratische Gleichung mit  als variablen (das ist die sogenannte Charakteristische Gleichung). wenn du sie löst erhälst du 2 lösungen: als variablen (das ist die sogenannte Charakteristische Gleichung). wenn du sie löst erhälst du 2 lösungen: 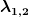 . Diese Beiden Lösungen werden als Fundamentalsystem bezeichnet. . Diese Beiden Lösungen werden als Fundamentalsystem bezeichnet.
=c_1 \cdot e^{\lambda_1 t})
=c_2 \cdot e^{\lambda_2 t})
|
Sehe ich das rchtig? Als erstes setze ich das die gleichung mit den Ableitungen in meine Ausgangsgleichung ein, danach erhalte ich 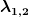 und das setze ich dann in die voher eingesetzte Gleichung? und das setze ich dann in die voher eingesetzte Gleichung?
| bottom hat Folgendes geschrieben: |
Die sogennante Linearkombination dieser beiden speziellen Lösungen ergibt dann die allgemeine Lösung:
=c_1 \cdot e^{\lambda_1 t}+c_1 \cdot e^{\lambda_2 t})
hierbei handelt es sich um die allgemeine Lösung der dgl. Diese beinhaltet unterschiedliche Fälle (für unterschiedliche starke Dämpfung). Du bist warsch interessiert an der lösung für die schwache dämpfung (die gleichung die du schon oben genannt hast).
versuch doch mal dass soweit nachvollzuziehen, dann kann ich dir noch zeigen wie man von da zum speziellen fall der schwachen dämpfung kommt.
gruß bottom |
Hmm, kann ich nicht einfach:
=c_1 \cdot e^{\lambda_1 t}+c_1 \cdot e^{\lambda_2 t})
nehmen und einfach einsetzen (dafür müsste ich dann ja nur  die Wellenlänge die Wellenlänge  , die Ausbreitungsgeschwindigkeit einstzen oder?) , die Ausbreitungsgeschwindigkeit einstzen oder?)
Falls das nicht so ist (so sieht es für mich aus) dann Frage ich:
Wieso gibt es unterschiedliche Lösungen für starke und schwache Dämpfungen und woher weißt du, dass ich eine Schwache Dämpfung brauche? Ach was ist eigentlich schwach und stark in diesem Zusammenhang?
Laut Aufgabe soll ich übrigens ein Prog schreiben Das mit die Auslenkung plottet. einmal mit 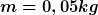 , , 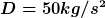 und und 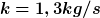 . .
Danach soll ich k varieren.
und: ich bin nur hier m die DGL zu lösen und nicht um das Programm zu schreiben (Ein Plot Programm zu schreiben sollte ich noch hinbekommen).
Entschuldige die Rechtschreibehller, ich muss noch ein bisschen Englisch machen und hab keine Zeit mehr. |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 13. Mai 2009 23:41 Titel: Re: DGL gedämpfte Schwingungen MI Verfasst am: 13. Mai 2009 23:41 Titel: Re: DGL gedämpfte Schwingungen |
 |
|
Ich möchte keine Verwirrung stiften, indem ich mich in den mathematischen Lösungsteil einmische.
Daher nur zu den Variablen ein paar Kommentare, weil ich das Gefühl habe, dass da noch ein wenig Klärungsbedarf besteht:
| Zitat: |
*Stop* wo kommt dieser Ansatz her?! und das soll doch =c\cdot e^{(\lambda t)}) heißen oder? heißen oder?
Ist das  da die Wellenlänge und das da die Wellenlänge und das  die Ausbreitungsgeschwindigkeit? die Ausbreitungsgeschwindigkeit?
|
Ja, das soll es heißen. Und nein, lambda ist NICHT die Wellenlänge und c NICHT die Ausbreitungsgeschwindigkeit.
Zur Zeit sind das nur irgendwelche Variablen.
Das Lambda ist quasi die Lösung der von bottom angesprochenen "charakteristischen Gleichung" (die wiederum vom Eigenwertproblem kommt - aber das braucht dich zum Lösen nicht unbedingt zu interessieren). Das Ding heißt einfach lambda. Du könntest es auch 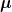 oder sonstwie nennen, aber traditionell heißt es halt lambda. Es gibt leider nicht genügend Buchstaben, damit nie Verwirrung aufkommen kann oder sonstwie nennen, aber traditionell heißt es halt lambda. Es gibt leider nicht genügend Buchstaben, damit nie Verwirrung aufkommen kann  . .
Das c wiederum ist auch nicht die Ausbreitungsgeschwindigkeit, es ist einfach eine Variable, die von den Anfangsbedingungen deines Systems abhängt. Sagen wir einmal du hast eine Diffgleichung zweiter Ordnung (höchste Ableitung = Ordnung) der einfachsten Form gegeben:
= t)
Wie löst du diese? Mit einem doppelten Integral über  - soviel Analysis solltet ihr schon gemacht haben. Wenn du nun integrierst, bekommst du bei jeder Integration Konstanten hinzu (eine pro Integration). - soviel Analysis solltet ihr schon gemacht haben. Wenn du nun integrierst, bekommst du bei jeder Integration Konstanten hinzu (eine pro Integration).
Und so ist es hier: Die DGL ist zweiter Ordnung, also hat die Lösung zwei freie Parameter (c1 und c2), die physikalisch von den Anfangsbedingungen deines Systems (Auslenkung am Anfang + Startgeschwindigkeit) abhängen. Wie genau, das wirst du dann selbst ausrechnen  . .
Gruß
MI
PS:
| Zitat: |
Ich hab sogar ein paar Lehrer genervt, die mir aber nicht direckt weiter helfen konnten. |
Was schon bedenklich ist! Zumindest ein Physiklehrer sollte in der Lage sein, diese DGL zu lösen, weil es einfach eine der bekanntesten DGL ist. |
|
 |
bottom

Anmeldungsdatum: 04.02.2009
Beiträge: 333
Wohnort: Kiel
|
 bottom Verfasst am: 14. Mai 2009 00:45 Titel: Re: DGL gedämpfte Schwingungen bottom Verfasst am: 14. Mai 2009 00:45 Titel: Re: DGL gedämpfte Schwingungen |
 |
|
Achja, eine sache hatte ich noch vergessen. bevor du den exponentialansatz benutzt, solltest du noch folgende umformungen mit deiner dgl machen. das ist nur dafür da, um später den physikalischen zusammenhang besser hinzubekommen:
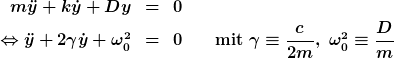
| m12lk hat Folgendes geschrieben: |
Ja ich bin mir sicher. Bei den Ableitungen kann ich ja 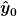 einfach ausklammern (muss ich ja nicht ableiten). Dann erhalte ich nach dem einsetzen einfach einfach ausklammern (muss ich ja nicht ableiten). Dann erhalte ich nach dem einsetzen einfach 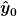 mal den Rest gleich null. mal den Rest gleich null. |
ok, aber dann muss doch nicht automatisch 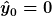 sein, es könnte doch auch dieser gesammte rest insgesammt null ergeben (was physikalisch gesehen mehr sinn macht). sein, es könnte doch auch dieser gesammte rest insgesammt null ergeben (was physikalisch gesehen mehr sinn macht).
| m12lk hat Folgendes geschrieben: | Sorry die Erklärung warum das nicht geht hab ich nicht verstanden 
|
also, deine erste idee einfach die schwingungsgleichung wie du sie aus der schule kennst zu nehmen und in die dgl einzusetzen, war schonmal sehr gut. sollte man denken, dass das auch funktioniert, da die schwingungsgleuchung ja eine lösung der dgl ist und damit diese erfüllen müsste. das problem ist aber, dass diese gleichung für die gedämpfte schwingung wie wir sie in der schule kennen lernen ein weinig vereinfacht ist, die eigendliche lösung der dgl ist noch ein wenig komplexer.
| m12lk hat Folgendes geschrieben: | | Damit hab ich kein Problem. Morgen ist schon mein Weg zur Bückerei geplant... Das Dumme ist, mir fehlen fast alle Grundlagen (bin erst 12.) |
 mehr als interesse brauch man nicht um sowas zu verstehen! (ich bin auch erst in der 13., sprich gerade mitten im abi) mehr als interesse brauch man nicht um sowas zu verstehen! (ich bin auch erst in der 13., sprich gerade mitten im abi)
| m12lk hat Folgendes geschrieben: |
*Stop* wo kommt dieser Ansatz her?! und das soll doch =c\cdot e^{(\lambda t)}) heißen oder? heißen oder?
Ist das  da die Wellenlänge und das da die Wellenlänge und das  die Ausbreitungsgeschwindigkeit? die Ausbreitungsgeschwindigkeit?
|
hast recht, da hab ich mich vertippt. habs oben verbessert.  und c sind einfach nur belibige konstanten, ohne physikalische bedeutung. man hätte sie auch mit belibigen anderen buchstaben bezeichnen können. und c sind einfach nur belibige konstanten, ohne physikalische bedeutung. man hätte sie auch mit belibigen anderen buchstaben bezeichnen können.
Zu dem ansatz: er hat sich einfach so als sinnvoll herausgestellt. das kann man folgendermaßen begründen: Notwendig und hinreichend dafür, dass der exponentialansatz =ce^{\lambda t}, ~t\in\mathbb{C}) eine lösung der homogenen DGL eine lösung der homogenen DGL 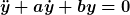 liefert, ist die charakteristische Gleichung liefert, ist die charakteristische Gleichung 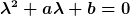 . Da jede quadratische Gleichung in der komplexen Zahlenebene (habt ihr schon über komplexe zahlen gesprochen?) mindestens eine Lösung hat, führt der exponentialansatz immer mindestens zu einer lösung. ob es da noch eine weitere begründung gibt weiß ich nicht. es ist wegen der oben genannten begründung einfach sinnvoll, eine exponentialfunktion als ansatz zu nehmen. . Da jede quadratische Gleichung in der komplexen Zahlenebene (habt ihr schon über komplexe zahlen gesprochen?) mindestens eine Lösung hat, führt der exponentialansatz immer mindestens zu einer lösung. ob es da noch eine weitere begründung gibt weiß ich nicht. es ist wegen der oben genannten begründung einfach sinnvoll, eine exponentialfunktion als ansatz zu nehmen.
| m12lk hat Folgendes geschrieben: | Sehe ich das rchtig? Als erstes setze ich das die gleichung mit den Ableitungen in meine Ausgangsgleichung ein, danach erhalte ich 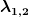 und das setze ich dann in die voher eingesetzte Gleichung? und das setze ich dann in die voher eingesetzte Gleichung?
|

du bestimmst also die lambdas, für die die exponentialfunktion die dgl erfüllt.
| m12lk hat Folgendes geschrieben: |
Wieso gibt es unterschiedliche Lösungen für starke und schwache Dämpfungen und woher weißt du, dass ich eine Schwache Dämpfung brauche? Ach was ist eigentlich schwach und stark in diesem Zusammenhang? |
wenn du 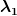 und und  bestimmt hast, siehst du dass da wurzelterme drinn sind, die etwa so aussehen könnten (musst du mal nachrechnen ob die bei dir exakt so aussehen): bestimmt hast, siehst du dass da wurzelterme drinn sind, die etwa so aussehen könnten (musst du mal nachrechnen ob die bei dir exakt so aussehen):
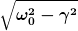
für den wurzelterm gibt es also in abhängigkeit von den parametern  und und 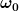 3 möglichkeiten: negativ, 0, positiv. 3 möglichkeiten: negativ, 0, positiv.
Jede dieser 3 möglichkeiten repräsentiert einen bestimmen physikalischen zustand (negativ-schwache dämpfung; positiv-starke dämpfung;0-übergang von schwacher zu starker, sogenannter aperiodischer grenzfall).
Dass diese 3 möglichkeiten wirklich die jeweiligen physikalischen umstände beschreiben kann man z.B. einfach durch betrachten der allgemeinen Lösung erkennen:
=c_1e^{\lambda_1 t}+c_2e^{\lambda_2 t})
wenn man jetzt in die lösungen der lambdas entsprechende werte einsetzt so dass eine der 3 situationen oben zustande kommt kann man die funktion beispielsweise plotten und man sieht dass die 3 möglichkeiten ziehmlich unterschiedlich aussehen.
die schwache dämpfung ist einfach die gedämpfte schwingung wie du sie aus dem unterricht kennst. die starke dämpfung ist kein schwingung mehr, sondern eine sogenannte aperiodische kriechbewegung, d.h. wenn du den oszillator auslenkst und dann loslässt nähert er sich langsam der ruhelage an und bleibt dort stehen. der aperiodische grenzfall ist auch eine aperiodische kriechbewegung (also keine schwingung) und stellt genau den übergang zwischen den beiden anderen fällen dar.
| m12lk hat Folgendes geschrieben: |
Laut Aufgabe soll ich übrigens ein Prog schreiben Das mit die Auslenkung plottet. einmal mit 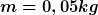 , , 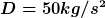 und und 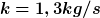 . .
Danach soll ich k varieren.
und: ich bin nur hier m die DGL zu lösen und nicht um das Programm zu schreiben (Ein Plot Programm zu schreiben sollte ich noch hinbekommen).
|
find ich cool, dass du dich über die eigendliche aufgabe hinaus dafür interessierst. 
ich hab jetzt echt irgendwie ziehmlich viel geschrieben, ich hoffe du kannst damit was anfangen.
gruß bottom
----------------------------------------------------------------
EDIT: oh, die antwort von MI hatte ich ganz übersehen.
| Zitat: | | Was schon bedenklich ist! Zumindest ein Physiklehrer sollte in der Lage sein, diese DGL zu lösen, weil es einfach eine der bekanntesten DGL ist. |
bedenklich - ja! die ausnahme? leider nein 
da könnte ich dir auch noch viele schlimme geschichten erzählen....
_________________
 |
|
 |
m12lk
Gast
|
 m12lk Verfasst am: 14. Mai 2009 08:29 Titel: m12lk Verfasst am: 14. Mai 2009 08:29 Titel: |
 |
|
[quote=MI]
Was schon bedenklich ist! Zumindest ein Physiklehrer sollte in der Lage sein, diese DGL zu lösen, weil es einfach eine der bekanntesten DGL ist.
{/quote]
Ich glaub du zieht voreilig Schlüsse... 
Nicht direkt weiterhelfen = Ich habe nicht verstanden was mein Physiklehrer so schnell auf meine Antwot gemeint hatte... (Hatte ja nur den Rest einer 5 min Pause...)
Naja und mein Mathelehrer meinter er könne das nicht jetzt mal ebenerklären...
Naja.
Gut das du mir sagtst dam meine schöne Gleichung ein weng vereinfacht ist  , das erklät dann alles. Warum hat das mein Phy Lehrer nicht erzählt? (Ich hab ihm auch meinen Lösungsansatz kurz gezeigt...) , das erklät dann alles. Warum hat das mein Phy Lehrer nicht erzählt? (Ich hab ihm auch meinen Lösungsansatz kurz gezeigt...)
Um ehrlich zu sein:
Von komplexen Zahlen weiß ich nur das 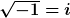 ist. (oder ich meine das zu wissen. Möglich ist, dass wir das in 11 gemacht haben. Jedoch war ich on 11 leider nicht da (Schüleraustausch). Ich werd mich mal erkundigen... ist. (oder ich meine das zu wissen. Möglich ist, dass wir das in 11 gemacht haben. Jedoch war ich on 11 leider nicht da (Schüleraustausch). Ich werd mich mal erkundigen...
Zu dem Rest nehme ich nach der Englisch Klausur Stellung  |
|
 |
m12lk
Gast
|
 m12lk Verfasst am: 14. Mai 2009 08:31 Titel: m12lk Verfasst am: 14. Mai 2009 08:31 Titel: |
 |
|
Ich glaub ich sollte mich registrieren ich kann meine Beiträge nicht korrigieren  |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 14. Mai 2009 10:43 Titel: MI Verfasst am: 14. Mai 2009 10:43 Titel: |
 |
|
| m12lk hat Folgendes geschrieben: | | MI hat Folgendes geschrieben: |
Was schon bedenklich ist! Zumindest ein Physiklehrer sollte in der Lage sein, diese DGL zu lösen, weil es einfach eine der bekanntesten DGL ist.
|
Ich glaub du zieht voreilig Schlüsse... 
Nicht direkt weiterhelfen = Ich habe nicht verstanden was mein Physiklehrer so schnell auf meine Antwot gemeint hatte... (Hatte ja nur den Rest einer 5 min Pause...)
Naja und mein Mathelehrer meinter er könne das nicht jetzt mal ebenerklären...
|
Ah, okay - dann will ich nichts gesagt haben. Für zwei oder drei Minuten wird's wirklich schwierig, das zu erklären  . . |
|
 |
Dragonfighter
Anmeldungsdatum: 07.03.2010
Beiträge: 5
|
 Dragonfighter Verfasst am: 07. März 2010 00:56 Titel: Dragonfighter Verfasst am: 07. März 2010 00:56 Titel: |
 |
|
Hallo,
ich hab gerade diesen Thread hier gefunden und er passt perfekt zu dem was ich nicht verstehe 
Also, ich schreibe gerade eine Facharbeit über DGL's und bin dabei über gedämpfte Schwingungen zu schreiben.
Kriechfall
aperiodischer Grenzfall
Bei den beiden Links ist mir was aufgefallen.
Ich habe in meiner Facharbeit in keinem der Fälle so etwas wie c1 und c2 erwähnt.
Dabei kam bei mir die Frage auf, was sind eigentlich c1 und c2?
Und warum kann ich beides vor die Funktion schreiben bzw. beim aperiodischen Grenzfall in (c1+c2t)?
In meiner Facharbeit bin ich beim aperiodischen Grenzfall zum Beispiel nur darauf eingegangen, dass auch s=s0*e^(-k/2m) (mit k als Dämpfungskoeffizienten) die Lösungsfunktion angibt.
Bis ich heute halt den Link gesehen hab und wegen dem c1 und c2 total verwirrt war.
Wäre toll wenn das jemand erklären könnte.
Vielen Dank im voraus.
Gruß
Dragon |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 07. März 2010 07:16 Titel: schnudl Verfasst am: 07. März 2010 07:16 Titel: |
 |
|
Physikalisch und unmathematisch argumentiert: Du machst ja den Ansatz
 = C e ^{k t})
und ermittelst k aus der charakteristischen Gleichung.
Da es für k - abgesehen vom aperiodischen Grenzfall - immer zwei Lösungen, k1, k2, gibt, gibt es auch zwei grundsätzliche Lösungen der DG, nämlich
 = C_1 e ^{k_1 t})
und
 = C_2 e ^{k_2 t})
die du je nach Belieben überlagern kannst:
 = C_1 e ^{k_1 t} + C_2 e ^{k_2 t})
Du brauchst die beiden unabhängigen Lösungen mit C1 und C2 schon alleine deshalb, da du mit einer einzigen Lösung gemäß
 = C_1 e ^{k_1 t})
zwar die Anfangsauslenung s(t=0)=C1 anzupassen vermagst, aber damit keinen Freiraum mehr hast, auch die Anfangsgeschwindigkeit v(t=0) vorzugeben. Mit einer freien Variablen kann man eben nur eine Bedingung und nicht zwei erfüllen. Ein schwingungsfähges System hat aber immer zwei Freiheitsgrade, nämlich s und v !
Für den Kriechfall ist die Lösung für die beiden k gemäß
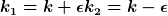
weswegen die allgemeine Lösung so aussieht:
 = e^{k t} \cdot \left( C_1 e^{\epsilon t} + C_1 e^{-\epsilon t}\right))
Für
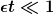
kann man die Exponentialfunktion annähern durch
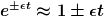
und aus der Lösung wird
 \approx e^{kt} \cdot \left((C_1+C_2)+(C_1-C_2)\epsilon t \right))
was man mit neuen Konstanten schreiben kann
 \approx e^{kt} \cdot \left(c_1+c_2t \right))
Für den aperiodischen Grenzfall gilt die Näherung exakt, da  = 0 ist. = 0 ist.
Ein Mathematiker würde diese Erklärung zwar in der Luft zerreissen, aber für Physik reicht sie alle male aus...

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 22. Apr 2010 15:39, insgesamt einmal bearbeitet |
|
 |
Dragonfighter
Anmeldungsdatum: 07.03.2010
Beiträge: 5
|
 Dragonfighter Verfasst am: 07. März 2010 13:00 Titel: Dragonfighter Verfasst am: 07. März 2010 13:00 Titel: |
 |
|
Ok angekommen ist, ich brauche jeweils Startgeschwindigkeit und Startauslenkung also quasi für den Zeitpunkt t=0
Aber warum kann ich zum Beispiel sagen, dass ich die Anfangsauslenkung bei  = C_1 e ^{k_1 t}) habe? habe?
Da könnte ich doch genauso gut auch die Anfangsgeschwindigkeit haben oder?
verstehen würde ich es, wenn bei

beide k's gleich wären weil ich dann ausklammern könnte...
http://de.wikibooks.org/wiki/Schwingbewegungen
Auf der Seite hier ist beim aperiodischen Grenzfall folgendes zu lesen:
"Diese Lösung hat jedoch nur eine Integrationskonstante und kann daher nicht die allgemeine Lösung sein. Aus der Theorie der Differentialgleichung ist jedoch bekannt, dass in diesem Fall  eine Lösung ist, [...]" eine Lösung ist, [...]"
Aber erstmal warum Integrationskonstante? Ich integriere doch gar nicht -.-
Und zum anderen wie komme ich auf Bt wenn das t eigentlich im Exponenten steht?

Vielen Dank im voraus. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 07. März 2010 14:02 Titel: schnudl Verfasst am: 07. März 2010 14:02 Titel: |
 |
|
Leider kann ich dir nicht ganz folgen...
I.A. ist die Geschwindigkeit und die Auslenkung zum Zeitpunkt t=0 gegeben.
z.B.
=x_0v(0)=v_0)
Dann musst du die beiden Konstanten, C1 und C2 so bestimmen, dass
 = C_1 e^{k_1 t}+C_2 e^{k_2 t})
 = \dd x(t)/\dd t = k_1 C_1 e^{k_1 t}+k_2 C_1 e^{k_2 t})
zum Zeitpunkt t=0 genbau diese Anfangswerte ergeben:
Also

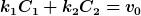
Dieses Gleichungssystem kann man nach C1 und C2 auflösen, wenn x(0) und v(0) gegeben ist. Mit nur einem C wirst du dir schwer tun, beide Bedimngungen zu erfüllen...Möglicherweise habe ich aber deine Frage falsch verstanden.
Die beiden Konstanten C1 und C2 sind fei wählbare Konstanten. Da man das Lösen einer Differenzialgleichung auch Integrieren nennt, heissen diese auch Integrationskonstanten.
In deinem Link wird der Ansatz
 = e^{kt} (C_1 +C_2 t))
motiviert, indem darauf hingewiesen wird, dass
 = te^{kt} )
die Differenzialgleichung für den aperiodischen Grenzfall löst. Du musst es ja nur ausprobieren und wirst feststellen, dass dies der Fall ist.
Ganz Allgemein: wenn du eine lineare Differentialgleichung hast, und diese verschiedene unabhängige Lösungen x1(t), x2(t), ...xn(t) hat, so ist auch jede Superposition dieser Lösungen wieder eine gültige Lösung: In unserem Fall sind die unabhängigen Lösungen
 = e^{k_1 t}
<br />
x_2(t) = e^{k_2 t})
Also ist
 = C_1 x_1(t) + C_2 x_2(t))
wieder eine Lösung, nämlich die allgemeinst mögliche.
Für den aperiodischen Grenzfall geht dies über in:
)
da k1 = k2 = k.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 22. Apr 2010 15:40, insgesamt 2-mal bearbeitet |
|
 |
Dragonfighter
Anmeldungsdatum: 07.03.2010
Beiträge: 5
|
 Dragonfighter Verfasst am: 07. März 2010 17:44 Titel: Dragonfighter Verfasst am: 07. März 2010 17:44 Titel: |
 |
|
Ok, ich meine das jetzt soweit verstanden zu haben. Aber wie komme ich auf den Lösungsansatz  = te^{kt} ) ? ?
Und warum sollte ich überhaupt noch nach einer zweiten Lösungsfunktion suchen?
Das will ich irgendwie noch nicht so richtig verstehen.
 
Nebenbei, wie komme ich beim aperiodischen Grenzfall von =e^{- \delta t} (c_1 e^{i \omega t} + c_2 e^{-i \omega t})) zu zu =e^{- \delta t} (c_1 \cos ( \omega t)+ c_2 \sin( \omega t))) ? ? |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 07. März 2010 18:45 Titel: schnudl Verfasst am: 07. März 2010 18:45 Titel: |
 |
|
| Dragonfighter hat Folgendes geschrieben: | Ok, ich meine das jetzt soweit verstanden zu haben. Aber wie komme ich auf den Lösungsansatz  = te^{kt} ) ? ?
Siehe mein Posting weiter oben. hast du es nicht gelesen? Ich habe mir viel Mühe gemacht, es zu erklären...Dieser Ansatz löst eben die DG für den aperiodischen Grenzfall. Ich sagte ja, du sollst es bei Bedarf nachrechnen. Hast du das gemacht?
Und warum sollte ich überhaupt noch nach einer zweiten Lösungsfunktion suchen?
Weil es bei einer DG 2. Ordnung (meist) auch zwei unabhängige Lösungen gibt und die zweite Lösung für physikalisch sinnvolle Lösungen erforderlich ist (wie oben schon 2x besprochen). Wie soll eine allgemeine Lösung denn deiner Meinung nach aussehen?
Das will ich irgendwie noch nicht so richtig verstehen.
 
Nebenbei, wie komme ich beim aperiodischen Grenzfall von =e^{- \delta t} (c_1 e^{i \omega t} + c_2 e^{-i \omega t}))
Das beschreibt die gedämpfte Schwingung!
zu =e^{- \delta t} (c_1 \cos ( \omega t)+ c_2 \sin( \omega t)))
Natürlich kannst du es auf diese Form bringen, aber dann sind die c1 und c2 in beiden Gleichungen verschieden:
=e^{- \delta t} (c_1' \cos ( \omega t)+ c_2' \sin( \omega t)))
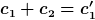
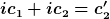
Wenn du von der gedämpften Schwingung kommst und dich dem APG annäherst, wie ist dann der Grenzwert dieser Gleichung? Die Überlegung entspricht genau meiner oben erwähnten, nur dass ich mich vom Kriechfall genähert habe.
|
Du solltest mal deine Gedanken ordnen...So würde ich die Facharbeit nicht abgeben 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Dragonfighter
Anmeldungsdatum: 07.03.2010
Beiträge: 5
|
 Dragonfighter Verfasst am: 07. März 2010 19:24 Titel: Dragonfighter Verfasst am: 07. März 2010 19:24 Titel: |
 |
|
Na ja Gedanken ordnen ich bin leicht überarbeitet...
Doch ich habe dein Posting gelesen aber ich glaube nicht, dass mir mein Lehrer abnimmt "Wenn ich es ausprobiere sehe ich, dass ich die zweite Lösungsfunktion richtig erraten habe".
Nächstes mal frage ich konkret wie leite ich das ganze mathematisch her 
Gedämpfte Schwingung meinte ich eigentlich auch *hust* |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 07. März 2010 20:13 Titel: schnudl Verfasst am: 07. März 2010 20:13 Titel: |
 |
|
| Dragonfighter hat Folgendes geschrieben: |
Nächstes mal frage ich konkret wie leite ich das ganze mathematisch her |
In
http://www.mathematik.uni-osnabrueck.de/lehre/analysisII03/kap17.pdf
Satz 17.1 findest du den Beweis. Aber es geht auch viel viel einfacher, indem du dich vom Kriechfall oder von der gedämpften Schwingung her annäherst: Da die Natur (hier) keine Sprünge macht muss die allgemeine Gleichung für den Fall der gedämpften Schwingung in jene für den aperiodischen Grenzfall fliessend übergehen. Erstere ist ja
 = e^{-\delta t}(C_1 \cos {\omega t} + C_2 \sin {\omega t}))
Verstehst du das noch? Falls ja, was passiert, wenn  gegen Null geht? Wir haben ja gegen Null geht? Wir haben ja
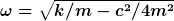
und der aperiodische Grenzfall tritt ein, wenn die Wurzel verschwindet.
Wie verhalten sich sin und cos für kleine Winkel, d.h. wenn

?
Tip:
 = e^{-\delta t} \sin {\omega t})
ist eine Lösung für den gedämpften Fall. Was passiert, wenn  sehr klein wird? sehr klein wird?
Ebenso:
 = e^{-\delta t} \cos {\omega t})
ist eine Lösung für den gedämpften Fall. Was passiert, wenn  sehr klein wird? sehr klein wird?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Dragonfighter
Anmeldungsdatum: 07.03.2010
Beiträge: 5
|
 Dragonfighter Verfasst am: 07. März 2010 23:06 Titel: Dragonfighter Verfasst am: 07. März 2010 23:06 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: |
In
http://www.mathematik.uni-osnabrueck.de/lehre/analysisII03/kap17.pdf
Satz 17.1 findest du den Beweis. Aber es geht auch viel viel einfacher, indem du dich vom Kriechfall oder von der gedämpften Schwingung her annäherst: Da die Natur (hier) keine Sprünge macht muss die allgemeine Gleichung für den Fall der gedämpften Schwingung in jene für den aperiodischen Grenzfall fliessend übergehen. Erstere ist ja
 = e^{-\delta t}(C_1 \cos {\omega t} + C_2 \sin {\omega t}))
Verstehst du das noch? Falls ja, was passiert, wenn  gegen Null geht? gegen Null geht? |
Dann müsste cos gegen 1 gehen und sin gegen 0.
| Zitat: |
Wir haben ja
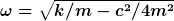
und der aperiodische Grenzfall tritt ein, wenn die Wurzel verschwindet.
Wie verhalten sich sin und cos für kleine Winkel, d.h. wenn

?
Tip:
 = e^{-\delta t} \sin {\omega t})
ist eine Lösung für den gedämpften Fall. Was passiert, wenn  sehr klein wird? sehr klein wird?
Ebenso:
 = e^{-\delta t} \cos {\omega t})
ist eine Lösung für den gedämpften Fall. Was passiert, wenn  sehr klein wird? sehr klein wird? |
Ich glaube ich weiß, worauf du hinauswillst.
Wenn cos gegen 1 geht und das ist ja der maximale Wert den cos annehmen kann wird das  immer kleiner das heißt die Funktion nähert sich insgesamt an 0 an. immer kleiner das heißt die Funktion nähert sich insgesamt an 0 an.
Die Sinusfunktion nähert sich ebenfalls an 0 an. Auch aufgrund der fortschreitenden Zeit aber auch, weil der Winkel immer kleiner wird oder? |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 08. März 2010 08:15 Titel: schnudl Verfasst am: 08. März 2010 08:15 Titel: |
 |
|
| Dragonfighter hat Folgendes geschrieben: |
Ich glaube ich weiß, worauf du hinauswillst.
Wenn cos gegen 1 geht und das ist ja der maximale Wert den cos annehmen kann wird das  immer kleiner das heißt die Funktion nähert sich insgesamt an 0 an. immer kleiner das heißt die Funktion nähert sich insgesamt an 0 an.
Die Sinusfunktion nähert sich ebenfalls an 0 an. Auch aufgrund der fortschreitenden Zeit aber auch, weil der Winkel immer kleiner wird oder? |
Nein, ich meinte etwas anderes:
 = C e^{-\delta t} \sin {\omega t})
ist ja eine Lösungklasse für den gedämpften Fall. Was passiert, wenn  sehr klein wird? Physikalisch bedeutet das, dass wir den apriodischen Grenzfall erreichen. Dazu entwickeln wir den sinus in eine Taylorreihe und erhalten in niedrigster Ordnung: sehr klein wird? Physikalisch bedeutet das, dass wir den apriodischen Grenzfall erreichen. Dazu entwickeln wir den sinus in eine Taylorreihe und erhalten in niedrigster Ordnung:
 = C e^{-\delta t} \cdot{\omega t})
Da wir für den Koeffizienten C keine Einschränkungen haben, kann man definieren
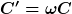
und bekommen eine Näherung für die obige Lösungsklasse
 \approx C't e^{-\delta t})
Wenn nun  immer kleiner wird, wird diese Näherung immer besser; bei immer kleiner wird, wird diese Näherung immer besser; bei  = 0 wird sie exakt. Daher ist die Funktion = 0 wird sie exakt. Daher ist die Funktion
 = C_1 t e^{-\delta t})
neben
 = C_2 e^{-\delta t})
eine Lösung der Differenzialgleichung für den aperiodischen Fall. Dass es wirklich so ist, überzeugt man sich durch Einsetzen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
|
|


























