| Autor |
Nachricht |
alex2007
Anmeldungsdatum: 23.11.2010
Beiträge: 76
|
 alex2007 Verfasst am: 23. Nov 2010 14:29 Titel: Rotation und Translation |
 |
|
Meine Frage:
Ein homgener Vollzylinder aus Eichenholz hat die Masse  und den Radius  . Er ist um die Zylinderachse drehbar gelagert. In den ruhenden Zylinder dringt das Geschoss ( ) einer Pistole ein. Die Geschossbahn verläuft senkrecht zur Achse und hat den Abstand  von ihr. Das Geschoss bleibt im Abstand  vor der Achse stecken. Nach dem Einschuss dreht sich das System mit einer Frequenz  . Welche Geschwindigkeit hatte das Geschoss unmittelbar vor dem Eindringen.
Meine Ideen:
Ich finde den Aufgabentext etwas verwirrend. Eigentlich ist das Energiethema recht einfach, aber hier werden soviele Informationen gegeben, die ich als unnütz erachte bzw. nicht recht weis, wozu ich sie brauche!
Als erstes brauch ich die Winkelgeschwindigkeit:
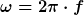
Jetzt hatte ich mir überlegt, dass ganze über die Energieerhltung zu berechnen. Doch hier liegt der Kniff meines Erachtens.
Normal wäre:
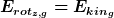
Also die Rotationsenergie des Systems aus Geschoss und Zylinder entspricht der kinetischen Energie des Geschoss vor dem Einschuss.
Allerdings ist mir aufgefallen, dass ja die Masse des Geschosses nicht verloren geht. Womit sich der Schwerpunkt des Systems verändert und somit nicht mehr im Drehunkt liegt, was zur Folge hat, dass ich auch nach dem Einschuss eine Translationsenergie des Geschosses habe:
 r_{z}^2) \omega^{2} + \frac{1}{2} m_{g} (\omega r_{2})^2 = \frac{1}{2} m_{g}v_{1}^2)
Soweit so gut. Das kann man alles schön zusammen fassen und könnte es auch ausrechenen. Allerdings habe ich das Gefühl etwas vergessen zu haben. Und zwar steht ja da, dass das Geschoss im Abstand  eintrifft und bei 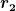 stecken bleibt. Ich habe in meiner Rechnung jetzt aber nur 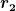berücksichtigt, da das Geschoss in disem Abstand den Mittelpunkt des Zylinders umkreist.
Die Farge ist nun, was mache ich mit ? Brauche ich das überhaupt? Das Geschoss gibt ja quasi einem Impuls an den Zylinder und wird dabei aber selbst gebremst und legt im Zylinder offensichtlich noch ein Stück weg zurück. Wie bringe ich dass in die Energiebilanz ein?
Danke
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 23. Nov 2010 16:31 Titel: |
|
|
|
Ich denke (angesichts der Massenverhältnisse und andere Unsicherheiten), daß die Aufgabe ganz einfach auf Drehung um die Zylinderachse angelegt ist und würde mit dem Drehimpulssatz anfangen. Mechanische Energie bleibt doch nicht.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 23. Nov 2010 16:53 Titel: |
|
|
Also ich denke, dass dein Ansatz mit der Energieerhaltung so schon mal richtig ist (verformungsenergie und Wärme mal vernachlässigt).
Dabei solltest du aber einfach die Masse des Geschosses vernachlässigen(<1% der Gesamtmasse) denke ich. Die wird wohl nur für den anfänglichen Impuls/Energie benötigt.
Das mit den Radien ist, denke ich, recht einfach. Es soll damit wohl nur klargestellt werden, dass die Energie in rotation gewandelt wird. wäre r1 = 0. würde sich das fass ja nicht drehen.
Bei der Rotationsenergie darfst du in denem Ansatz nur nicht die Masse ins Trägheitsmoment und die translationsbewegung stecken. Da wäre die Masse des geschosses ja doppelt berücksichtigt.
Für fortgeschrittene wäre eben noch die Reibung mit einzubringen, die du über die Bahn mitberechnen kannst. Wenn das geschoss entlang der Bahn einen Teil Energie an Reibung verliert und einen Teil in Drehmoment, bekommst du eine Bewegungsgleichung. Wird dann allerdings sehr kompliziert, denke ich 
|
|
|
alex2007
Anmeldungsdatum: 23.11.2010
Beiträge: 76
|
| alex2007 Verfasst am: 23. Nov 2010 17:00 Titel: |
|
|
Also du denkst, ich soll Impulserhaltung machen?
Also:
r_{z}^2 \omega )
Aber wäre das nichst angesichts der Aufgabenstellung zu leicht? Dann bräuchte ich weder  , noch  . Das kann doch nicht stimmen!?
|
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 23. Nov 2010 17:03 Titel: |
|
|
| mayap hat Folgendes geschrieben: | | verformungsenergie und Wärme mal vernachlässigt |
Warum?
| Zitat: | | wäre r1 = 0. würde sich das fass ja nicht drehen |
Jetzt wird nicht mehr vernachlässigt? [Übrigens kein Faß, sondern ein Vollzylinder; spielt für das Trägheitsmoment eine Rolle.]
Darf auf Analogie zum plastischen Stoß verweisen: Kein Erhalt der mechanischen Energie. Dort: Impuls, hier Drehimpuls als Erhltungsgröße.
dixi et salvavi animam meam.
Zuletzt bearbeitet von franz am 23. Nov 2010 17:09, insgesamt 2-mal bearbeitet |
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 23. Nov 2010 17:04 Titel: Re: Rotation und Translation |
|
|
ne, schon Energieerhaltung, aber wenn dann so:
 r_{z}^2) \omega^{2} + \frac{1}{2} m_{g} (\omega r_{2})^2 = \frac{1}{2} m_{g}v_{1}^2)
du hast die Masse einmal beim Trägheitsmoment (rotation) berücksichtigt und dann einmal als translationsbewegung.
Das Trägheitsmoment ist auch nicht ganz richtig gewesen, da die Masse des Geschosses ja nicht überall verteilt liegt, sondern an einer bestimmten Stelle.
Man muss nicht immer alle Angaben brauchen für die Lösung einer aufgabe
|
|
|
alex2007
Anmeldungsdatum: 23.11.2010
Beiträge: 76
|
| alex2007 Verfasst am: 23. Nov 2010 17:05 Titel: |
|
|
| mayap hat Folgendes geschrieben: | Das mit den Radien ist, denke ich, recht einfach. Es soll damit wohl nur klargestellt werden, dass die Energie in rotation gewandelt wird. wäre r1 = 0. würde sich das fass ja nicht drehen.
Bei der Rotationsenergie darfst du in denem Ansatz nur nicht die Masse ins Trägheitsmoment und die translationsbewegung stecken. Da wäre die Masse des geschosses ja doppelt berücksichtigt |
Ja aber die soll ja auch doppelt berücksichtig werden nicht? Insgesamt spalet sich die Energie doch in Rotation des Systems (das besteht nunmal aus der Gesamtmasse Geschoss+Zylinder) und in die kinetische Energie das Geschoss auf der Kreisbahn die es zurücklegt hat. Kinetische Energie heißt ja Bewegung des Schwerpunkts. Wenn der nicht mehr ganz genau im Zentrum des Zylinders ist (was er wegen der Geschossmasse nicht ist), dann bewegt er sich bei der Rotation, deswegen die Translationsenergie...oder nicht?
|
|
|
alex2007
Anmeldungsdatum: 23.11.2010
Beiträge: 76
|
| alex2007 Verfasst am: 23. Nov 2010 17:07 Titel: Re: Rotation und Translation |
|
|
| mayap hat Folgendes geschrieben: | ne, schon Energieerhaltung, aber wenn dann so:
du hast die Masse einmal beim Trägheitsmoment (rotation) berücksichtigt und dann einmal als translationsbewegung.
Das Trägheitsmoment ist auch nicht ganz richtig gewesen, da die Masse des Geschosses ja nicht überall verteilt liegt, sondern an einer bestimmten Stelle.
|
Ah ich glaube doch du hast rceht. Die Masse ist ja ersten vernachläsigbar klein und trägt somit kaum zur Rotation bei und außerdem ist sie an ner bestimmten Stelle. Du hast wohl recht.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 23. Nov 2010 17:17 Titel: |
|
|
| franz hat Folgendes geschrieben: | | mayap hat Folgendes geschrieben: | | verformungsenergie und Wärme mal vernachlässigt |
Warum?
|
Einfach: weil keine koeffizienten angegeben sind. Zudem für eine genaue Berechnung die exakte Art der Aufhängung der Achse nötig wäre, die nicht einmal angedeutet wird.
| franz hat Folgendes geschrieben: |
| Zitat: | | wäre r1 = 0. würde sich das fass ja nicht drehen |
Jetzt wird nicht mehr vernachlässigt? [Übrigens kein Faß, sondern ein Vollzylinder; spielt für das Trägheitsmoment eine Rolle.]
|
Wird noch immer vernachlässigt. Es wird einfach eine Beliebige Form eines Kraftstoßes angenommen. Man kann auch einfach in o.a. Gleichung + U für Verluste setzen.
| franz hat Folgendes geschrieben: |
Darf auf Analogie zum plastischen Stoß verweisen: Kein Erhalt der mechanischen Energie. Dort: Impuls, hier Drehimpuls als Erhltungsgröße.
|
Da hast du natürlich recht, Drehimpulserhaltung ist an Sich der schönere Weg hier, auch wenn auch dort genähert werden muss, da die Achse ein Drehmoment auffangen bzw. engegengeben wird und somit der Drehimpuls auch nicht ganz erhalten sein wird. Der Punkt am plastischen Stoß ist, dass sich beide Körper frei bewegen können.
Zuletzt bearbeitet von mayap am 23. Nov 2010 17:23, insgesamt einmal bearbeitet |
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 23. Nov 2010 17:19 Titel: Re: Rotation und Translation |
|
|
| alex2007 hat Folgendes geschrieben: |
Ah ich glaube doch du hast rceht. Die Masse ist ja ersten vernachläsigbar klein und trägt somit kaum zur Rotation bei und außerdem ist sie an ner bestimmten Stelle. Du hast wohl recht. |
Der Zylinder soll sich ja meines erachtens nur Drehen können, oder? da gibts dann keien translation mehr
Ob dus ins Trägheitsmoment reinrechnest, oder als translationsbewegung in einem Augenblick berechnest, macht keinen unterschied, kommt das gleiche raus
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 24. Nov 2010 09:54 Titel: |
|
|
also ich versteh auch nicht warum ihr hier unbedingt mit Energieerhaltung herumhantieren wollt, die trifft am wenigsten zu, wenn man nur bewegungsenergie betrachtet, man hat über den anderen Teil null angaben.
| Zitat: | Da hast du natürlich recht, Drehimpulserhaltung ist an Sich der schönere Weg hier, auch wenn auch dort genähert werden muss, da die Achse ein Drehmoment auffangen bzw. engegengeben wird und somit der Drehimpuls auch nicht ganz erhalten sein wird. Der Punkt am plastischen Stoß ist, dass sich beide Körper frei bewegen können.
|
reibungsfrei kann die Achse kein Drehmoment aufnehmen.
aber auch mit Reibung ist das der Drehmoment der Achse gering, weil die Reibkraft der Lagerung ja nicht am aussendurchmesser des Zylinders angreift sondern meistens ziemlich nah am Drehpunkt.
Das ist hier ein glasklarer Fall für die Drehimpulserhaltung.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 24. Nov 2010 16:20 Titel: |
|
|
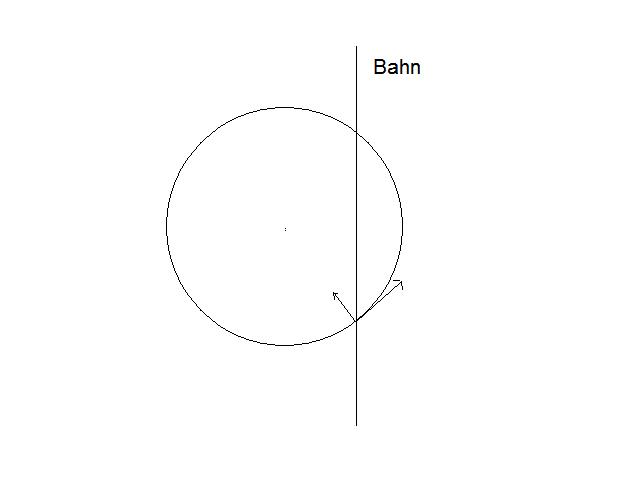
Der Drehimpuls ist hier ebensowenig erhalten, wie die kinetische Energie. Es wäre der Fall, wenn das Geschoss Kreisbogenförmig angreifen würde. Die Kraft, die das Geschoss auf den Zylinder ausübt ist nie senkrecht zur Achse. Dadurch hat man Kräfte auf die Achse, die nichts mit Reibung zu tun haben!
Wie in der (unschönen) Skizze zu sehen, gibt es einen sehr realen Anteil an Kraft, der direkt auf die Achse drückt. (hier für den Zeitpunkt des Auftreffens auf die Wand)
Dies führt zu Impulsverlust und damit Drehimpulsverlust. Diesen nimmt die Achse auf. Nichts mit Reibung.
Zudem wird die Kugel ja im Zylinder noch durch die beschleunigende Rotation in Richtung der Achse abgelenkt, was ein direkter Gewinn an Drehimpuls wäre.
Erhalten ist da was anderes. Wäre das ein Stoß, bei dem die Achse des Zylinders nicht befestigt wäre, wäre der Drehimpuls tatsächlich um jeden festen Punkt im Raum (nicht die Achse!! Da sie sich ja bewegen würde) erhalten. Da steht nur, dass sie gelagert ist.
| Beschreibung: |
|
| Dateigröße: |
10.68 KB |
| Angeschaut: |
8205 mal |
|
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 24. Nov 2010 19:13 Titel: |
|
|
ich glaube du sitzt hier einen Denkfehler auf.
Der Drehimpuls bezüglich der Drehachse bleibt erhalten.
Kräfte wie die Zentripetalkraft oder wie die von dir eingezeichneten radial Kräfte verändern den Drehimpuls bezüglich dieses Punktes nicht.
Und ich rede hier vom physikalischen Drehimpuls.
Man hat hier anders ausgedrückt eine Impulsmomenterhaltung.
Der Impuls der Geschosskugel hat auf den Drehachsen Punkt ein Impulsmoment dieses bleibt erhalten solange kein Reibung im Lager ist.
Alle Radial Kräfte verursachen kein Kraftmoment auf diesen Punkt
Die tangential Kräfte verursachen Kraftmomente belasten aber das Lager nicht mit einem Kraftmoment sondern tauschen sich untereinander zwischen Kugel und Zylinder aus.
Der Drehimpuls bleibt erhalten.
Das kann man sich generell merken wenn man den Bezuspunkt für die Impulsmomenterhaltung in die Drehachse legt dann ist der Drehimpuls immer erhalten, für alle andren Punkte müsste man die Impulsänderung der Erde plus Lager hinzuziehen.
|
|
|
alex2007
Anmeldungsdatum: 23.11.2010
Beiträge: 76
|
| alex2007 Verfasst am: 25. Nov 2010 02:15 Titel: |
|
|
Also was wäre nun deiner Meinung nach die Gleichung für den Ansatz der Lösung?
Und wieso soll Energiererhaltung nicht gehen? Wenn Impulserhaltung geht, dann geht auch Energieerhaltung. Drehimpuls und Rotationsenergie, sowie Impuls und kinetsiche Energie stehen jawohl in direktem Zusammenhang.
Oder willst mir jetzt was anderes erzählen?
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 04:11 Titel: |
|
|
ja das will ich 
Ich weiß nur nicht wie ich das jetzt umfassend erklären soll 
Die Energie bleibt nicht in Bewegung erhalten der Drehimpuls schon.
Energieerhaltung und Impulserhaltung sind immer gültig.
Dabei kommst drauf an was man betrachtet.
Die Impulsgleichungen handeln von Bewegung von Materie Masse mal Geschwindigkeit
Die Energie ist umfassender. neben bewegung gibts auch zum Beispiel verformung oder Erwärmung, das in den Impulsgleichungen in makroskopischer Sicht bei betrachtung von Körpern keine Rolle spielt.
Die Impulserhaltung beschreibt wie bewegungen erhalten bleiben.
Die Energieerhaltung beschreibt nicht wie bewegungen erhalten bleiben, dazu müssten man wissen wieviel Energie in Verformungen Erwärmungen und sonstige Formen übergehen.
Nur in Spezialfällen gilt der Erhalt der Bewegungsenergie.
Das Geschoss fliegt senkrecht im Abstand zur Drehachse 30mm es hat daher das Impulsmoment von
Das Impulsmoment um die Drehachse bleiben erhalten.
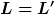
nachher = L' rotiert Geschoss und Zylinder mit omega um die Drehachse
und zwar die Kugel vereinfacht als Massepunkt am radius 35mm
rechne das mal aus und dann kontrollier mal ob hier die Bewegungsenergie erhalten bleibt.
es muß nachher weniger Energie in Bewegung erhalten sein, denn das Geschoss hat den Zylinder verformt.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 04:22 Titel: |
|
|
Nun, ich denke, dass hier zwei verschiedene Interpretationen der Aufgabe im Spiel waren. Meine Interpretation der Aufgabe war, dass das Geschoss auf einer geraden Bahn den Zylinder passieren soll. Dazu wären zusätzliche Momente nötig. Das wäre aber eine wesentlich kompliziertere Aufgabe und möglicherweise nicht die, die du lösen musst. Dazu müsste z.B. die Dichteveteilung im Zylinder anisotrop sein oder die achse reale ausdehnung haben.
Wenn einfach gemeint ist, dass die ungestörte Bahn an der Achse vorbeizöge, sich tatsächlich aber ab dem Eintritt eine Spiralförmige Bahn einstellt, die bei 35mm von der Achse entfernt endet und nicht näher beschrieben werden soll, kannst du das einfach mit Drehimpulserhaltung rechnen.
Wahrscheinlich habe ich die Aufgabe überschätzt und du sollst einfach den einfachsten Fall annehmen und mit Drehimpulserhaltung rechnen
Dazu ist wichtig, dass Energieerhaltung nicht gleich Impulserhaltung ist.
E = 1/2 mv^2, p = m*v
bei einem is nen quadrat, beim andern nicht.
Wenn ich also die Geschwindigkeit halbiere, die Masse verdoppele, hab ich gleichen Impuls, aber andere Energie! Impuls wäre in dem Fall erhalten, Energie nicht.
| VeryApe hat Folgendes geschrieben: |
Der Drehimpuls bezüglich der Drehachse bleibt erhalten.
|
Das ist nur in speziellen Fällen so (ruhende Achse, einfache Kreisbewegung etc.). Der Drehimpuls bleibt nur bzgl. eines fixen Punktes im Raum erhalten. Hier ist es zufälligerweise so, dass die Achse mit diesem Punkt übereinstimmt. Auch ist Drehimpulserhaltung noch bei Systemen gegeben, die keine Drehachse haben (Ellipsen, Geraden etc.)
| VeryApe hat Folgendes geschrieben: |
Impulsmomenterhaltung.
|
Was soll das denn sein? Impuls oder Moment?
| VeryApe hat Folgendes geschrieben: |
Der Impuls der Geschosskugel hat auf den Drehachsen Punkt ein Impulsmoment dieses bleibt erhalten solange Reibung im Lager ist.
Alle Radial Kräfte verursachen kein Kraftmoment auf diesen Punkt.
|
Drehmoment.
und eben solange tatsächlich nur radiale Kräfte angreifen. Und das ist ja gerade die Frage gewesen. Im allgemeinen Fall würde ich sagen nein, bei dieser Aufgabe ist es wahrscheinlich besser, das anzunehmen.
| VeryApe hat Folgendes geschrieben: |
Das kann man sich generell merken wenn man den Bezuspunkt für die Impulsmomenterhaltung in die Drehachse legt dann ist der Drehimpuls immer erhalten, für alle andren Punkte müsste man die Impulsänderung der Erde plus Lager hinzuziehen. |
Nein. Erde und Lager machen bei einer Bezugssystemänderung keinen prinzipiellen Unterschied. Die müssen genauso einberechnet werden. Der einzige Unterschied ist, dass Zentralkräfte dann eben nicht mehr Zentralkräfte sind.
Die Drehachse hat keine andere Bedeutung als dass bezüglich dieser bei einer sehr einfachen Kreisbewegung alle Kräfte Zentralkräfte sind. Ein sehr großer Vorteil für einfache Kreisbewegungen, im allgemeinen aber nutzlos.
Bekanntes Beispiel dass der Drehimpuls bezüglich einer Drehachse nicht erhalten ist, sind Kreisel. Dort sind Drehimpuls und Drehachse nicht parallel. Stichwort Präzession.
Oder z.B. Planetenbahnen. In den meisten Fällen gibt es keine Drehachse und wenn, ist der Drehimpuls um diese nicht erhalten.
Oder wenn in diesem Fall die achse nur endliche Steifigkeit besitzt, biegt sie sich durch und du hast schon keine mehr.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 05:12 Titel: |
|
|
| mayap hat Folgendes geschrieben: |
Nun, ich denke, dass hier zwei verschiedene Interpretationen der Aufgabe im Spiel waren. Meine Interpretation der Aufgabe war, dass das Geschoss auf einer geraden Bahn den Zylinder passieren soll. Dazu wären zusätzliche Momente nötig. Das wäre aber eine wesentlich kompliziertere Aufgabe und möglicherweise nicht die, die du lösen musst. Dazu müsste z.B. die Dichteveteilung im Zylinder anisotrop sein oder die achse reale ausdehnung haben.
Wenn einfach gemeint ist, dass die ungestörte Bahn an der Achse vorbeizöge, sich tatsächlich aber ab dem Eintritt eine Spiralförmige Bahn einstellt, die bei 35mm von der Achse entfernt endet und nicht näher beschrieben werden soll, kannst du das einfach mit Drehimpulserhaltung rechnen.
|
zunächst mal bezogen sich natürlich meine Kommentare auf eine starre Drehachse, was klar sein dürfte, hoff ich doch.
Was du da beschreiben willsd versteh ich nicht.
Egal was die Kugel da im Zylinder aufführt ob sie zick zack fliegt oder Purzelbäume schlägt, ist die Achse starr gelagert-> Drehimpuls bleibt erhalten.
| Zitat: |
Das ist nur in speziellen Fällen so (ruhende Achse, einfache Kreisbewegung etc.). Der Drehimpuls bleibt nur bzgl. eines fixen Punktes im Raum erhalten. Hier ist es zufälligerweise so, dass die Achse mit diesem Punkt übereinstimmt. Auch ist Drehimpulserhaltung noch bei Systemen gegeben, die keine Drehachse haben (Ellipsen, Geraden etc.)
|
siehe starre Drehachse..
wobei du sagst der drehimpuls bleibt nur bzgl eines fixen Punktes erhalten das stimme ich nicht überein. ich kann auch dynamische Punkte betrachten zu denen der Drehimpuls konstant bleibt.
| Zitat: |
Was soll das denn sein? Impuls oder Moment? smile
|
wie nennt sich bei dir Vektor mal Normalabstand?
bei mir heißt das Moment und davor die physikalische Größe die dazukommt.
Impuls=vektor mal Normalabstand Impulsmoment, Kraftmoment, Flächenmoment, and so on.
aber an dem solls nicht scheitern
| Zitat: |
Nein. Erde und Lager machen bei einer Bezugssystemänderung keinen prinzipiellen Unterschied. Die müssen genauso einberechnet werden. Der einzige Unterschied ist, dass Zentralkräfte dann eben nicht mehr Zentralkräfte sind.
|
genau das macht ja den Unterschied. somit erzeugen diese Kraftmomente
| Zitat: |
Bekanntes Beispiel dass der Drehimpuls bezüglich einer Drehachse nicht erhalten ist, sind Kreisel. Dort sind Drehimpuls und Drehachse nicht parallel. Stichwort Präzession.
|
kommt drauf an wie du das siehst wenn du immer in Richtung Drehachse siehst bleibt der Drehimpuls erhalten, wenn du natürlich universell Draufschaust dann ist das nicht mit meinen Angaben vergleichbar hier wirkt dauernd von aussen die Gewichtskraft drehend
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 15:35 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: |
zunächst mal bezogen sich natürlich meine Kommentare auf eine starre Drehachse, was klar sein dürfte, hoff ich doch.
Was du da beschreiben willsd versteh ich nicht.
Egal was die Kugel da im Zylinder aufführt ob sie zick zack fliegt oder Purzelbäume schlägt, ist die Achse starr gelagert-> Drehimpuls bleibt erhalten.
kurz gesagt: Achse, bzw. Lager mit endlicher Ausdehnung. Wenn diese nicht punktförmig ist, hält das Lager Drehmomente entgegen. Ob starr oder nicht.
| VeryApe hat Folgendes geschrieben: |
wobei du sagst der drehimpuls bleibt nur bzgl eines fixen Punktes erhalten das stimme ich nicht überein. ich kann auch dynamische Punkte betrachten zu denen der Drehimpuls konstant bleibt.
|
Fix im Sinne einer Galileitransformation. Und da sich die Achse selbst oBdA auch beschleunigt bewegen kann, ist sie keiner dieser Punkte.
| VeryApe hat Folgendes geschrieben: |
wie nennt sich bei dir Vektor mal Normalabstand?
bei mir heißt das Moment und davor die physikalische Größe die dazukommt.
|
Ich denke du meinst nicht Abstand, sondern Abstandsvektor, abr in diesem Falle ist das das Drehmoment. nicht jedes Moment kommt so zustande, siehe Trägheitsmoment (auch wenn mans theoretisch als Kreuzprodukt schreiben könnte:) )
Impulsmoment, Kraftmoment, Flächenmoment sind im allgemeinen sehr wenig gebräuchliche sysnonyme für das Drehmoment. Impulsmoment wird glaub nur in Holland verwendet...
| VeryApe hat Folgendes geschrieben: |
genau das macht ja den Unterschied. somit erzeugen diese Kraftmomente
|
Womit trotzdem der Drehimpuls erhalten bleibt. Allgemein ist mit Drehimpulserhaltung gemeint, dass die zeitl. Änderung des Drehimpulses gleich der Summe der auftretenden Drehmomente ist, nicht, dass es nirgendwo Kraftmomente gibt. Und dazu muss der Abstand zu einem festen Punkt berechnet werden.
| VeryApe hat Folgendes geschrieben: |
kommt drauf an wie du das siehst wenn du immer in Richtung Drehachse siehst bleibt der Drehimpuls erhalten, wenn du natürlich universell Draufschaust dann ist das nicht mit meinen Angaben vergleichbar hier wirkt dauernd von aussen die Gewichtskraft drehend |
|
1. Nein. Welche der 3 allgemeinen Drehachsen der Kreiselbewegung soll das denn sein? Dort ist es absolut offensichtlich nicht so, da sich die Drehgeschwindigkeit periodisch ändert und keine Momente wirken.
2. Die Achsen drehen beschleunigt umeinander. Nicht Galileotransformierbar. In diesem Fall ist dann die sog. Drehimpulsachse
3. Gewichtskraft wirkt so und so (sonst hast du nen massiven Fehler bei der Rechnung gemacht)
4. Gewichtskraft wirkt nicht drehend, sondern konstant.
5. Was soll denn ein "universelles draufschauen" sein? Hast du da ein ausgezeichnetes Bezugssystem gefunden?
So am Rande, du weisst schon, dass Der Drehimpuls ein Vektor ist, und dass wenn du sagst, dass alles, was senkrecht zum Drehimpuls ist, irrelevant sein soll, es nur sein kann, dass das, was du für die Drehachse sagst, eigentlich für den Drehimpuls/die Drehimpulsachse gilt? Man rechnet ja auch mit Drehimpuls und nicht mit einem Vektor, der Parallel zu einer evtl. vorkommenden Drehachse ist.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 16:04 Titel: |
|
|
also zunächst muß ich sagen das ich Physik nicht studiert habe, deswegen verstehe ich nicht genau was du meinst und du wahrscheinlich nicht genau was ich meine.
Also ohne Skizzen kommen wir nicht klar
Fangen wir an zum Thema starres Lager befestigt mit der Erde.
Und bitte bleiben wir in der klassischen Mechanik bei der Gallilei Transformation.
Starr bedeutet keine Formveränderung es bleibt wie es ist.
Mit der Erde verbunden bedeutet praktisch stillstand, da schwere Masse Geschwindigkeitsänderung null komma Josef
| Beschreibung: |
|
Download |
| Dateiname: |
Drehimpulserhaltung.gif |
| Dateigröße: |
18 KB |
| Heruntergeladen: |
2482 mal |
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 16:20 Titel: |
|
|
Die Kraft steht hier als synonym für beliebige Kräfte, komplett egal in welche Richtung.
Die Kugel hat ein Impulsmoment m*v*r auf den Lagerpunkt LP
Es wirkt eine Kraft, da wir die Kugel als Massepunkt annehmen wirkt diese natürlich im Schwerpunkt, wir können die Kugel auch mit räumlicher Ausdehnung annehmen, die Drehimpulserhaltung gilt trotzdem müssen aber dann auch die Rotation um den Schwerpunkt der Kugel berücksichtigen.
betrachten wir einen abschnitt dt
die Kugel verliert Impuls von m*v-F*dt.
was bezogen auf den LP bedeutet (m*v-F*dt)*r=m*v*r-F*dt*r
der Zylinder erhält ein Impulsmoment von F*r*dt
das was die Kugel verliert erhält der Zylinder.
Die zentripetalkraft bringt uns eine Geschwindigkeit nach innen. diese hat aber bezogen auf den Lagerpunkt keinen radius. denn das Kraftmoment durch Radialkräfte ist null und somit auch das Impulsmoment. Die Geschwindigkeit wirkt in Richtung lagerpunkt. v*r=v*0=0.-
Der Drehimpuls bleibt erhalten egal welche Kräfte wirken.
Nimmt man nun zum Beispiel den Punkt P2.
so hat die Kugel das Impulsmoment m*v*-r2
das Impulsmoment des Zylinders bleibt auch auf r2 gleich den er rotiert um seinen Schwerpunkt. den er wird durch ein Drehmoment zwei betragsgleiche entgegengesetzte Kräfte beschleunigt. Bei Rotation um den Schwerpunkt ist die Summe der Impulse null und somit bleibt sein Impulsmoment zu jeden Bezugspunkt gleich. Genauso wie das Drehmoment das auf den Zylinder wirkt. es ist auch auf r2 gleich, da auch die Summe der Kräfte auf den Zylinder null ist. denn es ist F*(r+r2) - F*r2 =F*r genauso wie bei LP.
die Kugel verliert
(m*v-F*dt)*-r2 =-m*v*r2+F*dt*r2
der Zylinder erhält aber F*r*dt
da r ungleich r2 oder nicht unbedingt gleich ist gilt nicht mehr L=L' wenn man nur Zylinder und Kugel betrachtet.
was fehlt ist das reactio des Zylinders auf das Lager nun muß der Impuls des Lagers mit berücksichtigt werden.
auf das Lager selbst wirkt eine Kraft nach unten. was auf Punkt P2 bedeutet
-F(r+r2) das Lager erhält ein Impulsmoment von -F(r+r2) *dt auf P2
Es gilt jetzt
-m*v*r2=[-m*v*r2+F*dt*r2] + [ F*r*dt] - [F(r+r2) *dt]
-m*v*r2=Drehimpuls Kugel + Drehimpuls Zylinder + Drehimpuls Lager
für die Drehimpulserhaltung müssen wir nun das Lager hinzuziehen. Im ersten Fall können wir darauf verzichten.
Aber nicht ganz denn wir haben noch eine Radialkraft Zentripetalkraft auch diese müssen wir auf r2 mitberücksichtigen denn sie beeinträchtigt die geschwindigkeit der Kugel.
Alle Punkt ausser LP machen einem das Leben schwerer. und genau das meinte ich , bei anderen Punkten muß man Lager mitberücksichtigen.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 17:18 Titel: |
|
|
| mayap hat Folgendes geschrieben: | Ich denke du meinst nicht Abstand, sondern Abstandsvektor, abr in diesem Falle ist das das Drehmoment. nicht jedes Moment kommt so zustande, siehe Trägheitsmoment (auch wenn mans theoretisch als Kreuzprodukt schreiben könnte:) )
|
Ich kenne keine Momente die nicht so zustande kommen auch das Trägheitsmoment
dm*r² ist nur eine durch Konstanten wegkürzte schreibweise von
dm*a*r und dm*a ist bekanntlich ein vektor und r der normalabstand.
wobei sich a durch zu alpha*r ergibt, umsonst hat man das nicht moment getauft.
aber das ist ja auch nicht Sache der Diskussion, das kann man sehen wie man will.
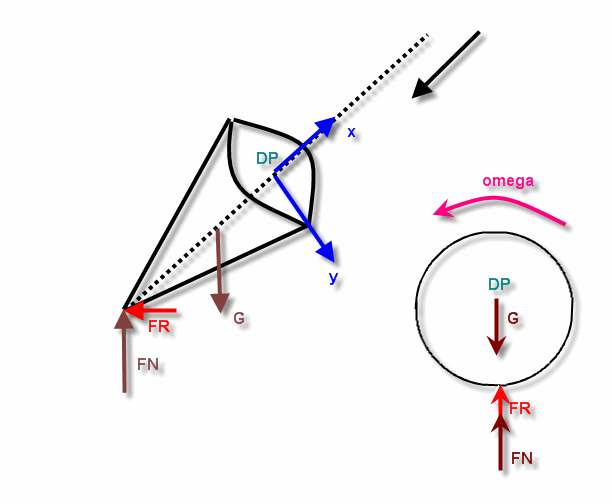
Zum Thema Kreisel Präzession. ich habe vorher geschrieben das man auch dynamische Punkte betrachten kann zu denen der Drehimpuls erhalten bleibt.
und zwar wenn man sein Koordinaten system mit ursprung in die Drehachse legt. Man hat ein mitbewegtes und natürlich auch einen mitbewegten Drehimpulsbilanz punkt.
| Beschreibung: |
|
| Dateigröße: |
20.29 KB |
| Angeschaut: |
7669 mal |
|
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:21 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | | also zunächst muß ich sagen das ich Physik nicht studiert habe, deswegen verstehe ich nicht genau was du meinst und du wahrscheinlich nicht genau was ich meine. |
Ich denke schon, dass ich weiss, was du meinst, nur sage ich eben, dass das nur ein sehr spezieller Fall ist, den du beschreibst. Und dass die Drehachse nur in speziellen Fällen besonders geeignet ist für Berechnungen, es ist eigentlicht die Drehimpulsachse, die du meinst, hier liegt sie ist es zufälligerweise auf der Drehachse.
(Wenn du mit dem Auto auf dem Äquator stehst, sagst du typischerweise nicht, dass der Äquator im Auto ist).
| VeryApe hat Folgendes geschrieben: |
Fangen wir an zum Thema starres Lager befestigt mit der Erde.
|
mit dem Wichtigen Zusatz, dass es keine Ausdehnung hat, oder, wie man es auch formulieren mag, in exakt einem Punkt befestigt ist.
Wenn du nicht weisst, was ich damit meine, ist dass eine Dicke Achse, die nicht im Schwerpunkt gelagert ist, sondern in einem Kreisring um diesen.
Als Maschinenbauer wird so etwas durchaus mitberechnet werden müssen.
| VeryApe hat Folgendes geschrieben: |
Die Kugel hat ein Impulsmoment m*v*r auf den Lagerpunkt LP
|
Was soll denn m*v*r sein? meinst du vielleicht r x p? Und gewöhne dir das Wort Impulsmoment ab, falls du mal Physik studieren willst, allgemein ist nämlich Moment Synonym für Impuls (u.a. im englischen Impuls = momentum) und das macht eben wenig sinn. (Impulsimpuls? )
| VeryApe hat Folgendes geschrieben: |
Es wirkt eine Kraft, da wir die Kugel als Massepunkt annehmen wirkt diese natürlich im Schwerpunkt, wir können die Kugel auch mit räumlicher Ausdehnung annehmen, die Drehimpulserhaltung gilt trotzdem müssen aber dann auch die Rotation um den Schwerpunkt der Kugel berücksichtigen.
|
Wie gesagt, das war die Frage. WENN MAN ANNIMMT, dass tatsächlich NUR Zentralkräfte wirken, lässt sich das ganze einfach wie vor 10 posts beschrieben berechnen.
| VeryApe hat Folgendes geschrieben: |
betrachten wir einen abschnitt dt
die Kugel verliert Impuls von m*v-F*dt.
was bezogen auf den LP bedeutet (m*v-F*dt)*r=m*v*r-F*dt*r
der Zylinder erhält ein Impulsmoment von F*r*dt
das was die Kugel verliert erhält der Zylinder.
|
wieder ist L = r x p! Das Kreuzprodukt! Bei dieser Gleichung würdest du alle Richtungsabhängigkeiten einfach komplett ignorieren!
| VeryApe hat Folgendes geschrieben: |
Die zentripetalkraft bringt uns eine Geschwindigkeit nach innen. diese hat aber bezogen auf den Lagerpunkt keinen radius. denn das Kraftmoment durch Radialkräfte ist null und somit auch das Impulsmoment. Die Geschwindigkeit wirkt in Richtung lagerpunkt. v*r=v*0=0.-
|
wieder:
Wie gesagt, das war die Frage. WENN MAN ANNIMMT, dass tatsächlich NUR Zentralkräfte wirken, lässt sich das ganze einfach wie vor 10 posts beschrieben berechnen.
| VeryApe hat Folgendes geschrieben: |
Der Drehimpuls bleibt erhalten egal welche Kräfte wirken.
|
Sinn des Impulserhaltungssatzes.
| VeryApe hat Folgendes geschrieben: |
Nimmt man nun zum Beispiel den Punkt P2.
so hat die Kugel das Impulsmoment m*v*r2
das Impulsmoment des Zylinders bleibt auch auf r2 gleich den er rotiert um seinen Schwerpunkt. den er wird durch ein Drehmoment zwei betragsgleiche entgegengesetzte Kräfte beschleunigt. Bei Rotation um den Schwerpunkt ist die Summe der Impulse null und somit bleibt sein Impulsmoment zu jeden Bezugspunkt gleich. Genauso wie das Drehmoment das auf den Zylinder wirkt. es ist auch auf r2 gleich, da auch die Summe der Kräfte auf den Zylinder null ist. denn es ist F*(r+r2) - F*r2 =F*r genauso wie bei LP, die Kugel verliert
(m*v-F*dt)*r2 =m*v*r-F*dt*r2
der Zylinder erhält aber F*r*dt
da r ungleich r2 oder nicht unbedingt gleich ist gilt nicht mehr L=L' wenn man nur Zylinder und Kugel betrachtet.
was fehlt ist das reactio des Zylinders auf das Lager nun muß der Impuls des Lagers mit berücksichtigt werden.
Aber nicht ganz denn wir haben noch eine Radialkraft Zentripetalkraft auch diese müssen wir auf r2 mitberücksichtigen denn sie beeinträchtigt die geschwindigkeit der Kugel.
Alle Punkt ausser LP machen einem das Leben schwerer. und genau das meinte ich , bei anderen Punkten muß man Lager mitberücksichtigen. |
Berücksichtigen muss man die Kraft in jedem Fall, auch im Fall r(LP) =0, sie hat einfach im Falle, dass sie Senkrecht zum Drehimpulsvektor steht, keine Auswirkung auf den Drehimpuls. Mag so aussehen, dass das aufs selbe rauskommt, nur ist die Ursache anders.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 17:23 Titel: |
|
|
der schwarze Pfeil erklärt die Blickrichtung, die Blickrichtung wandert mit der Drehachse mit das Koordinatensystem ebenfalls und auch der Bilanzpunkt.
Während ein Kreisel seine Präzession beschreibt bekommt man immer dasselbe Bild wie rechts unten eingezeichnet.
Der Drehimpuls bezüglich DP muss erhalten bleiben, da alle angreifenden Kräfte kein Kraftmoment ausüben.
wie gesagt ein Bilanzpunkt muß nicht starr im Raum bleiben, wer sagt das.
zum Thema Gewichtskraft, die Gewichtskraft dreht mit der Bodenkraft, dadurch wird auch aus einem ruhenden System betrachtet der Drehimpulsvektor umgelenkt, die Reibkraft lenkt die Schwerpunktsgeschwindigkeit um.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 17:32 Titel: |
|
|
es geht hier nur um den 2 dimensional Schnitt in dem die Achse eine Drehung erlaubt. die radien stellen immer die Normalabstände der vektoren zum Drehpunkt da.
Ich glaub ich weiß was du meinst, wenn die Kugel zum Beispiel von oben schräg herab auf den Zylinder stösst dann wird der Teil der in die Tiefe geht verschluckt.
Aber es weiß doch jeder das man den Schnitt senkrecht für die Drehachse benützen muß, in diesem Schnitt bleibt alles erhalten.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:36 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: |
Ich kenne keine Momente die nicht so zustande kommen auch das Trägheitsmoment
dm*r² ist nur eine durch Konstanten wegkürzte schreibweise von
dm*a*r und dm*a ist bekanntlich ein vektor und r der normalabstand.
wobei sich a durch zu alpha*r ergibt, umsonst hat man das nicht moment getauft.
aber das ist ja auch nicht Sache der Diskussion, das kann man sehen wie man will.
|
Nein, wenn Definitionen nicht eindeutig sind, sind sie falsch und führen zu falschen Ergebnissen. Das ist nicht Ansichtssache.
Du solltest dir vielleicht mal klar darüber werden, was Skalarprodukt, skalares Produkt und Kreuzprodukt ist. Dipolmoment = p = q*l, Drehmoment: L = r x p. Btw. Allgemein kann jeder beliebige Vektor durch irgendeine Form der Multiplikation dargestellt werden. Ist deiner Meinung nach jeder vektor ein Moment?
| VeryApe hat Folgendes geschrieben: |
Zum Thema Kreisel Präzession. ich habe vorher geschrieben das man auch dynamische Punkte betrachten kann zu denen der Drehimpuls erhalten bleibt.
und zwar wenn man sein Koordinaten system mit ursprung in die Drehachse legt. Man hat ein mitbewegtes und natürlich auch einen mitbewegten Drehimpulsbilanz punkt. |
Nein, weil das kein Inertialsystem ist und nicht galileitransformierbar.
Ein rotierendes System ist NICHT Inertialsystem!!
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:39 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: |
Aber es weiß doch jeder das man den Schnitt senkrecht für die Drehachse benützen muß, in diesem Schnitt bleibt alles erhalten. |
Das steht explizit in der Aufgabenstellung. Nur weil irgendwas schön ist, muss man nicht die Aufgabe so wählen, dass es schön wird. Wenn es nicht in der Aufgabe stünde, müsste man den allgemeinen Fall berechnen. Schiefe Bahnen.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:40 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: |
wie gesagt ein Bilanzpunkt muß nicht starr im Raum bleiben, wer sagt das.
|
niemand. Er muss galileitransformierbar sein.
| VeryApe hat Folgendes geschrieben: |
Der Drehimpuls bezüglich DP muss erhalten bleiben, da alle angreifenden Kräfte kein Kraftmoment ausüben.
|
gerade in diesem Punkt Greift die Gravitationskraft ja an. Sonst gäbe es eine Präzession. Das heisst es GIBT momente!
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 17:46 Titel: |
|
|
Frage verstehst du das schnittbild?
frage wenn du mit der Blickrichtung in Drehachse mitwanderst.
wie erscheint omega für dich dann , bleibt es konstant oder nicht?
Du schaust in jeder Stellung immer in Blickrichtung drehachse.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:49 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | Frage verstehst du das schnittbild?
frage wenn du mit der Blickrichtung in Drehachse mitwanderst.
wie erscheint omega für dich dann , bleibt es konstant oder nicht?
Du schaust in jeder Stellung immer in Blickrichtung drehachse. |
Omega bleibt gleich, impuls und damit drehimpuls ändert sich. Wie gesagt, KEINE Galileitrafo!! Du befindest dich in einem drehenden, also beschleunigten Bezugssystem! dafür gibt es keinen Impulserhaltungssatz.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 17:50 Titel: |
|
|
| mayap hat Folgendes geschrieben: |
VeryApe hat Folgendes geschrieben:
Aber es weiß doch jeder das man den Schnitt senkrecht für die Drehachse benützen muß, in diesem Schnitt bleibt alles erhalten.
Das steht explizit in der Aufgabenstellung. Nur weil irgendwas schön ist, muss man nicht die Aufgabe so wählen, dass es schön wird. Wenn es nicht in der Aufgabe stünde, müsste man den allgemeinen Fall berechnen. Schiefe Bahnen.
|
lol 
wir schreiben da schon Aufsätze über den Käse, ich muß jetzt was arbeiten, sonst krieg ich die ganze wochen nur Kartoffelsuppe.
Ich will nur noch mal auf die Angabe hinweisen. da steht ganz klar senkrecht auf die Drehachse.
| mayap hat Folgendes geschrieben: |
Omega bleibt gleich, impuls und damit drehimpuls ändert sich. Wie gesagt, KEINE Galileitrafo!! Du befindest dich in einem drehenden, also beschleunigten Bezugssystem! dafür gibt es keinen Impulserhaltungssatz.
|
der Drehimpuls auf DP ändert sich also , für mich aber nicht  in diesen Schnittbildern, wie sollte auch
MFG
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:57 Titel: |
|
|
Genau das habe ich ja geschrieben. Aber da steht z.B. nichts von punktförmiger Lagerung etc.
90% der Posts geht ja darum, dass es wie geschrieben, nicht allgemein Drehachsen sind, um die der Drehimpuls konstant ist, sondern die Drehimpulsachse.
Ich muss auch arbeiten, wollte ich auch gerade schreiben
zur Klärung der Drehungen lies am besten mal nach. Otten: Repetitorium der Experimentalphysik Kap. 7 ist dafür evtl. geeignet. Und merke vor allem Drehimpuls ist ein Vekor! Er ist das Kreuzprodukt aus Abstandsvektor und Impuls, nicht das Skalarprodukt! Dieser ist auch der einzige Vektor, um den Drehimpulsbetrachtungen einfach werden.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 17:58 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | der Drehimpuls auf DP ändert sich also , für mich aber nicht in diesen Schnittbildern, wie sollte auch
|
Genau für dich tut er es. Beschleunigte Bezugssysteme nachschlagen. Winkelgeschwindigkeit nicht gleich Drehimpuls!!
Noch ein allgemeiner Tipp: Mach dir gedanken über die Physikalischen Größen und setze nicht alles gleich!
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Nov 2010 18:14 Titel: |
|
|
jetzt muß ich doch noch was schreiben.
Schnittbilder haben an sich das man die Umgebung zwei dimensional beschreibt. Man kann sich auch zwei dimensional durch die WElt kämpfen und aufs richtige kommen.
Wenn du mir jetzt sagst der drehimpuls sei ein drei dimensionaler vektor, dann ist das natürlich auch glasklar, aber ich kann diesen auch zweidimensional betrachten, deswegen hab ich auch schnittbild gesagt.
denn im Schnittbild geht immer eine Komponete des Vektors verloren und somit bleibt er in diesem Schnittbild konstant.
der 3d dimensionale vektor bleibt natürlich nicht konstant.
In der Technik besteht das ganze Leben aus Schnittbildern.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 18:21 Titel: |
|
|
Genau hier darfst du das eben nicht machen und eine komponente einfach weglassen. Diese ist nämlichnicht konstant.
Schnittbilder sind nur 2dimensionale Projektionen und diese sind nicht immer konstant. Man muss die richtige wählen. Die 2dimensionale Welt ist nicht gleich der dreidimensionalen. Deshalb kommst du ja auch hier auf falsche Ergebnisse. Kannst ja nicht einfach die Gravitation oder 3. Komponente ignorieren, was du hier aber tust.
Nicht nur in der Technik, in der ganzen Physik sind solche"Schnittbilder" wichtig. Allgemein sind das Symmetrien und nur deshalb gibt es Erhaltungssätze.
| Zitat: | | Schnittbilder haben an sich das man die Umgebung zwei dimensional beschreibt. Man kann sich auch zwei dimensional durch die WElt kämpfen und aufs richtige kommen. |
Ganz ganz ganz ganz falsch!!! Nicht alles Besitzt eine Symmetrie, die das erlaubt. Man kann gar nicht sagen, wie falsch das ist....
In manchen Fällen braucht man auch 4 oder 11 oder unendlich viele Dimensionen.
Sorry, aber das ist sowas von falsch, bitte vergiss sofort, dass man alles 2dimensional darstellen kann.
Wer hat dir denn versucht, sowas zu erzählen???? Solche Annahmen können real gefährliche Auswirkungen haben!! Das ist echt der Hammer.
Zuletzt bearbeitet von mayap am 25. Nov 2010 18:30, insgesamt einmal bearbeitet |
|
|
hm
Gast
|
| hm Verfasst am: 25. Nov 2010 18:29 Titel: |
|
|
kann es sein das du hier DP als räumlich Fixpunkt betrachtest und nicht als in den Schnittbilder mitbewegter,
denn bei mir wäre der drehimpuls bezügich eines mitbewegten Punktes DP betrachtet in jeden Schnittbild.
immer nur Iszylinder* omega denn sonst gibts nichts drehimpuls mässiges auf diesen Punkt.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 18:33 Titel: |
|
|
Es gibt konstant die Gravitationskraft drauf. Wahlweise die Zenrtripetalbeschleunigung der Präzessionsbewegung. Diese rotiert in deinem Bezugssystem aus der ebene raus um deinen Drehpunkt. Dadurch erhältst du unterschiedlichste Drehmomente, die in deinem Bild unerklärlicherweise keine Winkelgeschwindigkeitsänderung hervorrufen.
Genau diesen Effekt nutzt man ja, um zu zeigen, dass sich die Erde, auf der wir leben, dreht.
Und genau deswegen ist es absolut falsch hier ein 2d schnittbild zu verwenden, dass alles erklären soll.
|
|
|
hm
Gast
|
| hm Verfasst am: 25. Nov 2010 18:39 Titel: |
|
|
Kräfte die aus der Ebene hinauswirken existieren 2dimensional nicht.
Ich wollte damit auch nicht die Kreiselbewegung erklären, sondern beschreiben was ich gemeint habe, das der Drehimpuls bezüglich eines dynamischen Punktes konstant sein kann und nichts anderes.
das dies nicht Präzessionsbewegung erklären kann ist klar denn die findet ja 3 dimensional statt.
Ich wollte damit zeigen das wenn in diesem Schnittbild keine Kraftmomente wirken und das tun sie auch nicht 2DIMENSIONAL dann bleibt auch der DREHIMPULS 2DIMENSIONAL erhalten gegenüber diesen dynamischen Punkt.
Aber nun wirklich jetzt geh ich
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 25. Nov 2010 18:46 Titel: |
|
|
Ja klar, wenn ich sage, es wirkt nichts, dann wirkt nichts.
Wenn du also die Kräfte ignorierst, kriegst du davon auch keine Wirkung. Stellst nur den Sachverhalt nicht dar. Sehr hilfreich??
Was meintest du dann mit
| Zitat: |
Während ein Kreisel seine Präzession beschreibt bekommt man immer dasselbe Bild wie rechts unten eingezeichnet.
Der Drehimpuls bezüglich DP muss erhalten bleiben, da alle angreifenden Kräfte kein Kraftmoment ausüben. |
Das, was du später als Schnittbild bezeichnest. Entscheide dich doch mal
Aber gut, dass du wenigstens eingesehen hast, dass nicht die ganze Welt mit 2d Bildern zu beschreiben ist, und die Drehachse keinen allgemeinen Vorteil hat...
|
|
|
alex2007
Anmeldungsdatum: 23.11.2010
Beiträge: 76
|
| alex2007 Verfasst am: 25. Nov 2010 23:53 Titel: |
|
|
Also nochmal zu eurer Diskussion. Es handelt sich hier um ne Übungsaufgabe aus "Experimentalphysik I" (Studiengang: Physik). Ich verfolge euer Gespräch und verstehe, dass es sich grundsätzlich um einen doch recht komplizierten Sachverhalt handelt, wenn man halt alles beachten will. Allerdings steht in der Aufgabe weder was von Reibung, Wärme oder Verformung, demzufolge sind diese Dinge AUSZUBLENDEN. Alles andere ist jetzt garnicht Thema. Wenn ich also von diesen Sachen absehe, dann nennt mir bitte einen Grund, warum ich hier Energieerhaltung nicht ansetzen kann? Das Geschoss hat kinetische Energie, trifft auf den Zylinder und versetzt ihn in Rotation. Allerdings Behällt auch das Geschoss eine Geschwindigkeit bei, die durch die Rotation hervorgerufen wird. Dennoch muss ich die Masse in der Rechnung erwähnen, da wenn ich die Kugel als einzelnen Körper betrachte er eben immernoch kinteische Energie besitzt, während er sich auf der Kreisbahn um die Achse im Abstand R2 bewegt. Also kintesiche Energie = Rotationsernergie plus kinetsiche Energie.
Das ist doch richtig. Alles andere verkompliziert die Aufgabe und ist heir wie gesagt nicht Thema.
Außerdem hatte jemand nen Denkfehler. Und zwar hat der Abstand r=30cm mit dem r=35cm garnichts zu tun. logisch kann man sich das mal an ner skizze erklären. Die 3cm sagen mir nur, dass überhaupt eine Rotation erzeugt wird. dass ist einfach der senkrechte abstand der Flugbahn zur Achse. Die 35cm sind der Abstand vom Gecshoss zum Mittelpunkt des Zylinders. Das isn großer Unterschied. Demzufolge ist r=30cm für die Rechnung irrelevant und meine Energiegleichung (bzw die berichtigte Version, dass die Masse der Kugel nur in der kinetischen Energie nach dem Stoß zu berücksichtigen ist) ist korrekt für die Lösung der Aufgabe.
Dennoch durchaus ne interessante Diskussion, wenn man sich überlegt,was in nem "realen Fall" alles beachtet werden müsste, dann wäre das ganze nicht so einfach.
Ich habe übrigens noch mehr Aufgaben zum Thema Energie, Impuls, bei Bewegungen auf Kreisbahnen (also auch Rotation). Kann gerne noch eine Stellen zur Diskussion. Denke ist kein uninteressantes Thema.
|
|
|
mayap
Anmeldungsdatum: 15.12.2009
Beiträge: 301
|
| mayap Verfasst am: 26. Nov 2010 00:39 Titel: |
|
|
Allgemein gilt ab dem Studium leider: Wenn etwas nicht angegeben ist, muss selbst abgeschätzt werden, ob es mitberücksichtigt wird oder nicht. Nur weil es nicht angegeben ist, heisst nicht, dass man es wie ein Schulkind einfach ignorieren darf. An der uni funktioniert das andersrum. Das heisst ALLES mitberücksichtigen. Wenn etwas vernachlässigt wird, MUSS man eine Erklärung parat haben. So einfach wie in der Schule isses da nicht mehr Notfalls müssen auch fehlende Angaben aus der Literatur nachgeschlagen werden.
Und gerade hier sollte der Verlust durch Verformung wohl mitberücksichtigt werden. Was ist denn der einzige Grund dafür, dass die Kugel steckenbleibt und überhaupt den Zylinder zur Drehung bewegt? Reibung! Und diese ist essenziell wichtig für diese Bewegung. Wenn man diese vernachlässigt, fliegt die Kugel einfach durch den Zylinder und nichts passiert. Ich denke das wäre nicht Sinn der Aufgabe
Der nächstrichtigere Weg wäre eben die Impulserhaltung. Das ist für eine ExI Vorlesung an sich sehr passend, da wäre einfache Energieerhaltung vielleicht etwas zu einfach
Wie franz bereits angemerkt hat, ist das Stichwort plastischer Stoß hier recht passend.
Sorry, dass dein Thread zu so weitreichenden Diskussionen ausgeartet ist, aber ich musste dann doch wenigstens die Grundlegendsten Dinge klarstellen, damit diese nicht verbreitung finden und dann zu Problemen führen
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
