| Autor |
Nachricht |
planck1858
Anmeldungsdatum: 06.09.2008
Beiträge: 4542
Wohnort: Nrw
|
 planck1858 Verfasst am: 04. Jul 2009 15:02 Titel: Herleitung s(t) gleichmäßig beschleunigte Bewegung [Formel] |
 |
|
Hallo,
wie kam man nochmal auf folgende Formel?
Diese kann man aus zwei, zu einer Formel umformen.
Die Ausgangsformel ist folgende.
Danke schon mal im Voraus!
_________________
Die Naturwissenschaft braucht der Mensch zum Erkennen, den Glauben zum Handeln. (Max Planck)
"I had a slogan. The vacum is empty. It weighs nothing because there's nothing there. (Richard Feynman) |
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
| wishmoep Verfasst am: 04. Jul 2009 16:56 Titel: |
|
|
Die Beschleunigung a ist die zweifache Ableitung des Weges nach der Zeit, umgekehrt ist der Weg das doppelte Zeitintegral der Beschleunigung.
Geht man nun davon aus, dass a konstant ist (ist bei gleichmäßiger Beschleunigung so), muss man zweimal integrieren.
\,\dd t = \int v\,\dd t = \frac{1}{2}\,a\cdot t^2)
Betrachtet man die Konstanten mit:
\,\dd t + c_{v} = \int v\,\dd t + c_{v} = \frac{a}{2}\,t^2+c_v+c_s) |
|
|
Zepto
Anmeldungsdatum: 03.10.2007
Beiträge: 323
|
| Zepto Verfasst am: 04. Jul 2009 17:06 Titel: |
|
|
| wishmoep hat Folgendes geschrieben: |
|
Da meintest du sicher:
 \,\dd t = \frac{1}{2} \cdot a \cdot t^2 + c_v\cdot t + c_s )
Ansonsten gibt es zum Beispiel auch graphische Möglichkeiten, wie man auf die Formel kommt.
Gruß
Zepto |
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 04. Jul 2009 17:07 Titel: |
|
|
Musst du  nicht auch integrieren ? 
Edit: Oh, da war jmd schneller |
|
|
planck1858
Anmeldungsdatum: 06.09.2008
Beiträge: 4542
Wohnort: Nrw
|
| planck1858 Verfasst am: 04. Jul 2009 17:21 Titel: |
|
|
Danke, aber das hilft mir noch nicht viel weiter, da ich noch nicht integriert habe, geschweige denn genau weiß, wie die Integralrechnung funktioniert und wie man ableitet.
_________________
Die Naturwissenschaft braucht der Mensch zum Erkennen, den Glauben zum Handeln. (Max Planck)
"I had a slogan. The vacum is empty. It weighs nothing because there's nothing there. (Richard Feynman) |
|
|
bottom
Anmeldungsdatum: 04.02.2009
Beiträge: 333
Wohnort: Kiel
|
| bottom Verfasst am: 04. Jul 2009 17:28 Titel: |
|
|
guckst du hier: klick!
_________________
 |
|
|
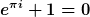Zepto
Anmeldungsdatum: 03.10.2007
Beiträge: 323
|
| Zepto Verfasst am: 04. Jul 2009 17:41 Titel: |
|
|
@pressure:  
| planck1885 hat Folgendes geschrieben: | | Danke, aber das hilft mir noch nicht viel weiter, da ich noch nicht integriert habe, geschweige denn genau weiß, wie die Integralrechnung funktioniert und wie man ableitet. |
Dann guck dir mal die Graphen hier an.
Der v(t) und der a(t) Graph sollten intuitiv klar sein. Auf den s(t) graph kommst du indem du zum beispiel die durchschnittsgeschwindigkeit über eine bestimmte Zeit nimmst, also bei  dann }{2}) .
Das ist die Fläche unter dem v(t) Graphen. Du kannst dir vorstellen, dass der gesamte zurückgelegte Weg sich immer aus der Summe der Produkte der momentangeschwindigkeit und der Zeitspanne in der die Momentangeschwindigkeit herrschte ergibt. Wenn du die Zeit also in sehr kleine Stücke hackst ( btw.: das dürfen wir ja, da die Quantenmechanik ja sagt, dass auch die zeit gequantelt ist.. ), dann bekommst du sehr viele kleine  Rechtecke unter deinem v(t) Graphen.
Wenn du das verstehst, hast du auch die Essenz der Integralrechnung begriffen. 
Gruß
Zepto |
|
|
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
| wishmoep Verfasst am: 04. Jul 2009 17:51 Titel: |
|
|
|
Ja... ja... soll mit integriert werden, man möge mir das Auf Grund des Wetters verzeihen... |
|
|
lambda
Anmeldungsdatum: 27.11.2007
Beiträge: 33
|
| lambda Verfasst am: 04. Jul 2009 23:11 Titel: |
|
|
Wenn du nicht integrieren kannst, nicht schlimm. Ein Integral berechnet einfach die Fläche unter dem Graphen. Bei einer gleichmäßigen Beschleunigung ist a=konst. D.h. die Geschwindigkeit wächst proportional zur Zeit t. Die Fläche ist also eine (rechtwinklige) Dreiecksfläche.
Nun kann man zwei Fälle betrachten. Einmal mit Anfangsgeschwindigkeit und ohne. Ohne hast du die normale Dreiecksfläche. Und da die Fläche gleich der Strecke ist, hast du die Strecke. Dann kannst du umformen und kommst zu deiner Gleichung. Dasselbe kannst du dann mit Anfangsgeschwindigkeit machen.
Solltest du dir mal aufzeichnen.
_________________
Gruß lambda
"Auch ein Dummkopf pflegt manchmal nachzudenken; aber immer erst nach der Dummheit"
Rousseau |
|
|
planck1858
Anmeldungsdatum: 06.09.2008
Beiträge: 4542
Wohnort: Nrw
|
| planck1858 Verfasst am: 05. Jul 2009 13:56 Titel: |
|
|
Ich möchte mich bei allen bedanken, die versucht haben mir das zu erklären.
@lambda, ein besonderer Dank gilt dir, du kannst wirklich gut erklären.
_________________
Die Naturwissenschaft braucht der Mensch zum Erkennen, den Glauben zum Handeln. (Max Planck)
"I had a slogan. The vacum is empty. It weighs nothing because there's nothing there. (Richard Feynman) |
|
|
bottom
Anmeldungsdatum: 04.02.2009
Beiträge: 333
Wohnort: Kiel
|
| bottom Verfasst am: 05. Jul 2009 14:15 Titel: |
|
|
| planck1885 hat Folgendes geschrieben: | | die versucht haben mir das zu erklären. |
hast du es denn verstanden?
_________________
|
|
|
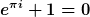para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 05. Jul 2009 15:37 Titel: |
|
|
| bottom hat Folgendes geschrieben: | | hast du es denn verstanden? |
... Und ist klar geworden, warum die Formel hier keine Gültigkeit besitzt?
_________________
Formeln mit LaTeX |
|
|
|
Registrieren
Login
FAQ
Suchen
