| Autor |
Nachricht |
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
 sembel Verfasst am: 18. Nov 2023 19:03 Titel: Formel gesucht: Winkelmaß für Erde um die Sonne |
 |
|
Hallo,
bin auf der Suche nach einer Formel zur Berechnung der Position der Erde um die Sonne in einem 360°-System für ein JavaScript Skript. Weil die Geschwindigkeit der Erde auf ihrer Bahn um die Sonne schwankt, benötigt es eine "Equation of Time" für diese, ähnlich der des "Analemma" (Sonne über Horizont am Meridian).
Als Nullpunkt sollen Windersonnenwenden verwendet werden. Also es soll ein tropisches Jahr verwendet werden. Der Grund dafür ist die Einhaltung der Jahreszeiten. 360° sind somit 31556925,261 Sekunden. Für eine gemittelte Ermittlung der Position würde dies genügen, indem per Unix Timestamp eine Berechnung durchgeführt wird. Die Umlaufbahn schwankt jedoch in ihrer Geschwindigkeit, weil ein bisschen unrund. Die Erde ist also 'mal schneller und 'mal langsamer. Die Ø Geschwindigkeit beträgt 29,7859 km/s. Im Perihel ist sie jedoch 30,29 km/s und im Aphel 29,29 km/s. Das wäre also auch noch irgendwie in die Berechnung einzubeziehen. Das wird ein bisschen schwierig, weil nicht eines von beiden als Nullpunkt verwendet wird. Eventuell benötigt es dazu eine Abstandsrechnung zwischen Windersonnenwende und Perihel. Desweiteren gibt es dann noch die Schlangenlinie der Erde um die Sonne, die auf dem Mond basiert. Ob diese jedoch wegen ihrer Marginalität relevant für das Ergebnis ist, ist fraglich (JavaScript = 21 Nachkommastellen).
Die erste Frage ist, an welchem Punkt die Schwankung der Geschwindigkeit wechselt und ob dieser immer gleich ist. Die zweite Frage ist, ob die Geschwindigkeit linear gleichmäßig beschleunigt/abbremst.
Die weiteren Fragen sind, ob es — in diesem Bezug — weitere Schwankungen gibt, die zu beachten wären.
Die allgemeine Frage ist, ob es bereits so eine Formel gibt und wo sie veröffentlicht ist. Auf Github sind einige atsronomische Skripte veröffentlich, nur ist mir nicht bekannt wie diese von mir gesuchte Formel in etwa aussieht, oder welchen Namen sie hat. Formeln für eot und Mond sind mir bereits bekannt. Es ist wohl wahrscheinlich, dass die von mir gesuchte Formel bereits existiert und nicht neu erfunden werden muss.
Davon abgesehen besteht auch die Frage, ob Windersonnenwenden als Nullpunkt praktikabel sind, oder eher ein Frühlingspunkt oder Perihel.
Das Ergebnis der Formel sollte eine Zahl (Float) zwischen 0 und 360 sein. Bevorzugt werden Formeln in Computersprache, wie JavaScript, PHP, Java und ähnlich.
Zuletzt bearbeitet von sembel am 23. Nov 2023 15:12, insgesamt 5-mal bearbeitet |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 19. Nov 2023 11:50 Titel: |
|
|
Hallo TomS, danke für deine Antwort und die Links.
Über Kepler's laws bin ich schon gestolpert, ist mir jedoch zu hoch. Bin eher eine Niete in Mathematik, außer was das Programmieren betrifft.
Mir geht es in der Sache um künstlerische experimentelle Intuitionen (reines Hobby). Da wurde von mir schon einiges gemacht. Soweit dazu komplizierte Formeln notwendig waren, konnten diese von mir gefunden werden. Meiner Erfahrung nach muss fast nichts stetig neu erfunden werden, weil es fast alles schon gibt. Es muss nur gefunden werden. Simpel gesagt, es wird ein (sagen wir mal) Vergaser benötigt, ohne einen Vergaser neu zu erfinden und ohne zu wissen wie er funktioniert. Naja, so grob schon, aber nicht bis ins letzte Detail. Das "Ergebnis" ist die Menge an Sprit in der Luft, oder irgendwie so.
Es geht also darum die Umlaufbahn der Erde um die Sonne in einem tropischen Jahr in 360 Teile (plus Nachkommastellen) zu unterteilen. 360 wegen dem Winkelmaß. Das klingt an sich sehr einfach, wenn eine gemittelte Zeit genommen wird. Aber wenn die Geschwindigkeitsschwankungen, die nicht zu einer Wintersonnenwende oder einem Frühlingspunkt wechseln, sondern an einem Perihel und Aphel, mit einbezogen werden, wird es kompliziert, und für mich zu hoch. Es ist dann kein einfacher Vergaser mehr, sondern ein sehr komplizierter mit mehreren Kanälen und Düsen (Fallstrom-, Primär-, Membran-, mit Höhenkompensation, ...).
Ich benötige etwas Untestützung im Bezug zu der Formel. Den Rest, also das künsterlische experimentelle, bekommen ich dann alleine hin.  Nebenbei zudem die Frage, welcher Nullpunkt am praktikalbelsten wäre. Mir würden rein ästhetisch Wintersonnenwenden taugen. Frühlingspunkte eher weniger. Perihel oder Aphel eher nicht. Es können auch zwei Formeln sein, die zusammenwirken.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 19. Nov 2023 13:15 Titel: |
|
|
Deine Denkweise (gemittelte Zeit bzw. Geschwindigkeit, Geschwindigkeitsschwankungen, Wintersonnenwende oder Frühlingspunkt …) ist zu kompliziert.
Wenn man die Literatur durcharbeitet, findet man grob zwei Perspektiven:
1) Die erste geht von einer geozentrischen Sicht aus, betrachtet die o.g. Punkte, Ekliptik, Präzession der Erdachse … Längengrade auf der Erdoberfläche … um zu immer genaueren Zeitgleichungen zu gelangen. Wenn das dein Ziel ist, dann gibt es nur den harten Weg.
2) Die zweite geht von zwei vereinfachten Annahmen aus und versucht, zwei Dinge zu verknüpfen:
i. einerseits rotiert die Erde um sich selbst, und zwar an einen Tag; würde sie bzgl. der Sonne stillstehen und nicht um diese rotieren, würde die Sonne nach exakt einem Tag an exakt der selben Position am Himmel stehen; so ist der Tag definiert.
ii. andererseits befindet sich die Erde auf einem Orbit um die Sonne, den sie in einem Jahr zurücklegt; auch für einen elliptischen Orbit gilt, dass dieser selbst nicht rotiert, d.h. nach exakt einem Jahr befindet sich Erde an exakt der selben Position bzgl. Sonne und Fixsternhimmel; so ist das Jahr definiert.
Nun rotiert die Erde jedoch um sich selbst, und die Erdachse hat eine feste Neigung ggü. dem Orbit um die Sonne, d.h. der Winkel, unter dem wir jeweils zur selben Uhrzeit (bezogen auf den Tag i.) die Sonne am Himmel sehen, ändert sich von Tag zu Tag, und ist nach einem Jahr (ii) wieder der selbe – fast!
Das zentrale Problem ist, dass 365 Tage (i.) also 365 Rotationen nicht exakt auf ein Jahr (ii.) d.h. auf eine Umrundung des Orbits führen. Warum sollte das auch so sein? Das schwierige d.h. aufwändige Problem ist, wie man beides unter einen Hut kriegt (anders als beim Quintenzirkel können wir Erdrotation und -orbit nicht temperiert stimmen). Dieses zentrale Problem existiert übrigens auch für exakt kreisförmige Kepler-Orbits.
Die Frage ist, was ist deine Zielsetzung: lokale Ortszeit, Zonenzeit … UTC, Sonnen- oder Sternjahr … worauf willst du hinaus? Möchtest du (d)eine lokale Position einnehmen? einfache nur pünktlich sein? oder sind Vegetationsperioden und Ernten wichtig? eine gedachte Position im Erdmittelpunkt? die eines oberhalb des Sonnensystems ortsfesten Beobachters der einige Jahrhunderte die Orbits der Planeten aufzeichnet? Abhängig davon wirst du unterschiedliche Definitionen für Tag und Jahr einführen.
So wie ich dich verstehe, geht es dir um das tropische Jahr, also ein Sonnenjahr. Möchtest du die wahre oder die mittlere Sonnenzeit betrachten?
Dann verstehe ich dich so, dass du Schwankungen der Umlaufgeschwindigkeit zunächst ignorieren möchtest, d.h. einen exakt kreisförmigen Orbit. Dann müssen wir zwei Feste Winkelgeschwindigkeiten betrachten, eine für die Rotation der Erde um ihre Achse, eine zweite für den Orbit. Klar soweit?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 19. Nov 2023 16:16 Titel: |
|
|
Vielen Dank auch für diese deine Antwort.
Ich bin auch so ein bisschen der Typ von learning by doing. In diesem Bezug jedoch nicht nur learning, sondern auch creating. Also es gibt eine Idee, aber kein Ideal, das verwirklicht werden will. Die Idee ist formbar, flexibel und passt sich an die Gegebenheiten an.
Dass alles schwankt, dass ist mir bereits bekannt, da ich schon etwas zu Sonne und Mond programmiert habe. Die Schwankungen, und eben auch der des Erdorbits um die Sonne, sind mein Interesse. Das tropische Jahr schwankt um ~±10 Minuten.
Eine Formel zur Berechnung einer Prozentzahl der Position der Erde um die Sonne in einem tropischen Jahr mit Nullpunkt Wintersonnenwenden habe ich nun programmiert. Dabei werden die Schwankungen der tropischen Jahren mit einbezogen. Die Berechnung der Wintersonnenwenden ist eine sehr umfangreiche Funktion, weswegen ich mich für bereits vorberechnete Zahlen entschieden habe, die im Internet kursieren.
Das aktuelle tropische Jahr: 31556340 Sekunden
Bei einem Timestamp von: 1700406179 (Heute, ~ 15:03 UTC)
Ist die Position der Erde im Bezug zur Sonne bei: ~91,1 % / 327,95°
Das wäre also schon einmal zielführend. Jetzt würde ich gerne die Schwankung der Geschwindigkeit der Erde um die Sonne mit einbeziehen. Eine Formel zur Berechnung habe ich nicht gefunden, bzw. nur eine zur Berechnung von Perihel und Aphel.
Es wird also jetzt — abgesehen vom bisherigen — eine Formel zur Berechnung der Geschwindigkeitsschwankung gesucht.
Wie mir scheint wird es sehr komplex diese Geschwindigkeitsschwankung in die Formel einzubauen, da die Wechsel dieser Schwankung autonom von Solstice und Equinox sind.
Die Frage ist, ob es im Bezug zur "Genauigkeit" (der Schwankung) Sinn macht diese Geschwindigkeitsschwankung mit einzubeziehen, oder ob sie zu marginal ist, dass sie gar nicht wesentlich auffällt.
PS: vermutlich muss ich eine Testberechnung machen, um die Zeitlängenunterschiede zwischen je Wintersonnenwende und Perihel sichtbar zu machen, um zu sehen, wie da die Schwankungen sind.
Das mit Tag im Jahr, also irgendein neu erfundenes Datum, interessiert erstmal nicht. Es geht erstmal nur um eine Zahl zwischen 0-360 (Position) mit Inkludierung einiger Schwankungen.
|
|
|
1741
Gast
|
| 1741 Verfasst am: 19. Nov 2023 17:41 Titel: |
|
|
Mir ist nicht klar, warum Du welche Genauigkeit willst. Ab einem gewissen Punkt (also, bei Betrachtung allerlei möglicher noch so kleiner Effekte) kommst Du aber um Infinitesimalrechnung nicht herum. Das Ergebnis ist dann keine geschlossene Lösung/Formel mehr. Ich zweifle daran, dass Du das mit JavaScript machen willst. Und wie mir scheint, brauchst Du diese Genauigkeit ohnehin nicht.
Du könntest Dir viel Arbeit ersparen, wenn Du einfach vorhandene, professionell berechnete, naturgetreue Daten verwenden würdest: ssd.jpl.nasa.gov/horizons/ Wenn Du magst, kannst Du diese ja noch transformieren und projezieren, so dass Deine Anforderungen an die Ergebnisse erfüllt sind.
|
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 19. Nov 2023 18:36 Titel: |
|
|
Wie schon Eingangs geschrieben:
| Zitat: | | Die Ø Geschwindigkeit beträgt 29,7859 km/s. Im Perihel ist sie jedoch 30,29 km/s und im Aphel 29,29 km/s. |
Wie viel diese Schwankung pro ° Abstand ausmacht, ist mir nicht bekannt. Ich gehe bisher davon aus, dass es relevant ist. Weitere Schwankungen, wie die Schlangenlinie durch den Mond bedingt, sind eher zu gering.
Zur Berechnung dieser Schwankung wird es wohl eine Sinuskurve benötigen, ähnlich wie bei eot. Exakt solch eine Formel suche ich.
Die Inkludierung dieser Schwankung wird jedoch wohl schwierig, weil der Wendepunkt der Geschwindigkeit nicht an Wintersonnenwenden ist, sondern vermutlich an Perihel und Aphel.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 19. Nov 2023 20:03 Titel: |
|
|
| sembel hat Folgendes geschrieben: | | Dass alles schwankt, dass ist mir bereits bekannt, da ich schon etwas zu Sonne und Mond programmiert habe. Die Schwankungen, und eben auch der des Erdorbits um die Sonne, sind mein Interesse. Das tropische Jahr schwankt um ~±10 Minuten. |
Bahnstörungen durch andere Planeten u.ä. wirst du nicht berücksichtigen können; das ist extrem aufwändig. Die einzige Lösung ist, dass du eine fertige Formel findest. Die erklärt aber nichts.
Aber wenn du das tust, musst du auch Kepler-Orbits berücksichtigen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 19. Nov 2023 20:13 Titel: |
|
|
|
Mal eine ganz simple Frage. Ist die eot Formel nicht sowieso schon das passende? Sie berechnet doch die Schwankung der Erdgeschwindigkeit?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 19. Nov 2023 20:24 Titel: |
|
|
Was ist "eot"?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 19. Nov 2023 21:06 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Was ist "eot"? |
Das ist die "equation of time"-Differenz in Sekunden. Diese wird auf die gemittelte Sonnenzeit aufgerechnet.
Hier gibt es eine Berechnung in JavaScript plus eine eindrucksvolle Visualisierung: https://github.com/benlansdell/analemma
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 19. Nov 2023 21:53 Titel: |
|
|
| sembel hat Folgendes geschrieben: | | Mal eine ganz simple Frage. Ist die eot Formel nicht sowieso schon das passende? Sie berechnet doch die Schwankung der Erdgeschwindigkeit? |
Ja, die einfachste Zeitgleichung berücksichtigt einige Schwankungen. Einflüsse von Mond und Planeten sind jedoch nicht berücksichtigt, das erfordert weitere Korrekturen.
Ich weiß nur noch nicht, worauf du eigentlich hinaus willst. Im Titel schreibst du von der Position der Erde, und das führt auf Kepler-Orbits. Andererseits diskutierst du sehr viel zur Zeitgleichung; zu deren Herleitung benötigt man ein Verständnis der Kepler-Orbits.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 20. Nov 2023 17:13 Titel: |
|
|
@TomS , ja, das führt hier irgendwie zu nix. Gesucht wird jemand, der entweder selbst Formel/Funktionen schreiben kann oder weiß wo diese zu finden sind.
Du hast scheinbar "Position" falsch verstanden. Nicht die Position am Himmel, oder interstellaren Raum, sondern auf dem Orbit, und da auf einer 360° Scala (Ring), ähnlich einer Winkelscheibe (rund). Siehe hier:
https://m.media-amazon.com/images/I/61nnN6Au4gL._AC_SL1200_.jpg
Es wird also n-Sekunde zu n-Grad gesucht. Sagen wir zu jedem vollen Grad die Sekunden als Unix Timestamp. Oder auch nur fortlaufende Sekunden ab 0.
| Code: | 0° - 360° = n Sekunden 1 tropisches Jahr (schwankend).
0° = 0 Sekunden (Wintersonnenwende)
1° = ? Sekunden
...
359° = ? Sekunden
360° = 0 Sekunden (Wintersonnenwende) |
Oder zu jeder Sekunde die Gradzahl. Das ist eigentlich besser.
| Code: | Aktuelles tropische Jahr: 31556340 Sekunden
0 Sekunden = 0° (Wintersonnenwende)
1 Sekunden = ?°
...
31556339 Sekunden = ?°
31556340 Sekunden = 360° (Wintersonnenwende) |
Da die Geschwindigkeit der Erde auf ihrem Orbit um die Sonne schwankt, wird ein EOT für diese Berechnung benötigt. Also ein EOT für den Orbit der Erde um die Sonne und nicht für das Analemma der wahren Sonnenzeit.
Perihel 30,29 km/s
Aphel 29,29 km/s
Perihel →abbremsen→ Aphel →beschleunigen→ Perihel
Wobei physikalisch auch "abbremsen" = beschleunigen.
Das EOT für das Analemma scheint dem EOT für den Orbit der Erde um die Sonne in etwa gleich zu sein.
Die Frage ist, ob die EOT für das Analemma gleich dem EOT für den Orbit der Erde um die Sonne ist. Der EOT für das Analemma hat ja auch was mit der Erdrotation zu tun, die ebenso schwankt. Die Erdrotation spielt aber bei meinem Experiment keine Rolle.
Mir scheint, dass du meine Fragen gar nicht beantworten kannst.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 20. Nov 2023 17:59 Titel: |
|
|
Also dann:
| sembel hat Folgendes geschrieben: | | Es wird also n-Sekunde zu n-Grad gesucht … zu jeder Sekunde die Gradzahl. Das ist eigentlich besser. |
Passt, das ist exakt das, was der Keplerorbit liefert (noch ohne dafür eine bestimmte Zeit wie UTC vorzugeben; das ist der zweite Schritt).
Du suchst den Winkel phi, den die Erde auf ihrem Orbit um die Sonne überstreicht, unter Berücksichtigung der variablen Geschwindigkeit, als Funktion einer Zeit t, die z.B. mit einer Atomuhr gemessen wird.
Ok?
| sembel hat Folgendes geschrieben: | | Gesucht wird jemand, der entweder selbst Formel/Funktionen schreiben kann … |
Kann ich.
| sembel hat Folgendes geschrieben: | | … oder weiß wo diese zu finden sind. |
Wenn du mir sagst, für welches Problem, dann kann ich das evtl. auch ;-)
| sembel hat Folgendes geschrieben: | | Du hast scheinbar "Position" falsch verstanden. Nicht die Position am Himmel, oder interstellaren Raum, sondern auf dem Orbit, und da auf einer 360° Scala (Ring), ähnlich einer Winkelscheibe (rund). |
Das hängt doch miteinander zusammen! Die Zeitgleichung geht von der Position am Himmel aus (lokale Zeit), setzt dies natürlich in Bezug zur Position auf dem Orbit, und natürlich liefert der Kepler-Orbit diese 360° Skala.
| sembel hat Folgendes geschrieben: | | Da die Geschwindigkeit der Erde auf ihrem Orbit um die Sonne schwankt, wird ein EOT für diese Berechnung benötigt. |
Nein, genau anders herum.
Der Kepler-Orbit liefert den Winkel und damit letztlich die Zeitgleichung. Nicht die Zeitgleichung den Keplerorbit.
| sembel hat Folgendes geschrieben: | | Mir scheint, dass du meine Fragen gar nicht beantworten kannst. |
Weil ich bisher noch keine Frage klar verstanden hatte.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 20. Nov 2023 18:49 Titel: |
|
|
OK, danke für deine Antwort TomS. Wie schon erwähnt ist bei mir zuerst eine Idee vorhanden und anfangs ziemlich vage. Alles weitere ergibt sich dann, oder auch nicht, je nach Möglichkeit/en. Bei dieser Sache spielen die Vorkenntnisse der Sonnen-EOT mit rein. Aber da ist das wohl etwas anders.
Es stimmt wohl, dass für mein Experiment nicht ein EOT gesucht wird, sondern es genügt die entsprechende Gradzahl (0-360) zu fortlaufender Zeit (Sekunden++). Die EOT könnte anhand dieses Ergebnisses berechnet werden, wenn gewünscht (im Vergleich zu gemittelten Werten).
Also ja, der Standort des "Betrachters", also der "Viewpoint" in dieser Angelegenheit, ist die Sonne. Hätte diese keine Eigenrotation und hätte diese Longitudes, so wäre es jeweils die Longitude, bei der die Erde am "höchsten" steht, und von diesem Zeitpunkt der Zeitstempel abgelesen wird. Oder umgekehrt vom Zeitstempel die Longitude.
Beispiel:
266587122 Unix Timestamp Sekunden = 158° Longitude
oder
158° Longitude = 266587122 Unix Timestamp Sekunden
Im Prinzip kommt die reine Position-Formel ohne Unix Timestamp aus. Dieser wird einfach nur aufgerechnet. Es benötigt nur einen Nullpunkt. Mir wären Wintersonnenwenden recht, die dann jeweils 0° und 0 Sekunden sind. Die Länge/n sind bekannt.
Winkel: 0-360°
Zeit: 0-31556340 Sekunden (Aktuelles tropische Jahr. Berechnet aus den vorberechneten Unix Zeitstempeln der Windersonnenwenden)
Eventuell ist solch eine Formel schon in dem zuletzt von mir verlinkten Github Repository vorhanden. Dort gibt es eine Funktion namens KeplerDynamics in der analemma.js. Allerdings geht es da um das Sonnen-Analemma auf der Erde.
https://github.com/benlansdell/analemma/blob/master/src/analemma.js#L210
Es gibt glaube auch Skripte zur Berechnung des Abstands der Erde zur Sonne. Da müsste sowas sicherlich inkludiert sein.
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
| Nils Hoppenstedt Verfasst am: 20. Nov 2023 19:13 Titel: Re: Formel gesucht: Kepler-Orbit Winkelmaß für Erde um die S |
|
|
| sembel hat Folgendes geschrieben: | | bin auf der Suche nach einer Formel zur Berechnung der Position der Erde um die Sonne in einem 360°-System für ein JavaScript Skript. |
Hi,
ich hab nicht alles gelesen, aber wieso integrierst du nicht einfach die newtonschen Bewegungsgleichungen? Das sind nur ein paar Zeilen Code und du erhältst die Bahnkurve und die Bahngeschwindigkeit in Abhängigkeit der Zeit.
Viele Grüße,
Nils
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 20. Nov 2023 20:39 Titel: |
|
|
|
@Nils , weil ich davon keine Ahnung habe und weil sehr wahrscheinlich diese Keplers Orbit Gleichung exakt das passende dafür ist.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 20. Nov 2023 21:44 Titel: |
|
|
| sembel hat Folgendes geschrieben: | | weil ich davon keine Ahnung habe |
Wenn Du die Ephemeridenberechnung hinbekommst, dann kannst Du das auch. Das ist kein Hexenwerk.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 20. Nov 2023 22:25 Titel: |
|
|
Ich gehe sogar noch weiter.
Die reine Berechnung des Kepler-Orbits, speziell des Winkels als Funktion der Zeit, ist deutlich einfacher als die Aufstellung einer Zeitgleichung, weil letztere i) zusätzlich die Erdrotation und ii) die Neigung der Erdachse berücksichtigen muss, also die Kombination zweier Rotation um zueinander geneigte Rotationsachsen, also ein dreidimensionales Problem.
Außerdem ist die Zeitgleichung mit der Relation "Ortszeit – mittlere Zeit" ein unnötiger Umweg, wenn man ohnehin nicht an der Ortszeit interessiert ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 20. Nov 2023 22:55 Titel: |
|
|
Also wenn es gerade um die Berechnung der Sonnenzeit-EOT geht, da habe ich keine Ahnung von der Formel. Ich benutze sie nur. Ich bin also sowas wie ein Nutzer, und kein Erfinder.
Die von mir benutzte Sonnenzeit-EOT-Formel benötigt Tag (im Monat) und Monat (im Jahr) als Input. Es gibt also nur 1 EOT pro Tag. Das genügt auch. Der Output ist ein Integer (positiv/negativ), dessen Größe der Unterschied zur gemittelten Zeit ist. Dieser EOT-Wert kann vielseitig verwendet werden, auch kreativ.
Von daher dachte ich — weil ich die gemittelte Zeit / Winkel mittels den vorberechneten Wintersonnenwenden-Timestamps per Dreisatz ausrechnen kann — wäre eine EOT für den Erdorbit um die Sonne ebenfalls nützlich. Diese EOT kann dann ebenso vielfältig verwendet werden.
Wenn es jedoch einfacher ist die Sekunden / Winkel direkt zu berechnen, dann geht das auch so und ist sogar um ein vielfaches besser, weil 1 Wert pro Sekunde / Grad anstatt nur 1 Wert pro Tag. Wer dann zusätzlich die EOT benötigt, kann sie sich per Gegenrechnen mit der gemittelten Zeit berechnen.
Schablone:
| Code: | <script>
function erdorbit_winkel(sekunden) {
var t = sekunden;
// Berechnung
return result;
}
var sekunden_seit_wintersonnenwende = 12345;
var winkel_float = erdorbit_winkel(sekunden_seit_wintersonnenwende);
// Verwendung
</script> |
Zuletzt bearbeitet von sembel am 21. Nov 2023 16:56, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 21. Nov 2023 13:08 Titel: |
|
|
Hier mal eine kurze Zusammenfassung für den Winkel als Funktion der Zeit. Ich sehe 4 recht einfache Ansätze zur Lösung; Nummer (3) muss ich nur nochmal anschauen.
Ich starte mit einigen Begriffen, die man im Umfeld des Keplerproblems benötigt.
Große bzw. kleine Halbachse der Ellipse: a bzw. b
Parameter der Ellipse: p
Kleinster bzw. größter Bahnradius, allgemein Periapis bzw. Apoapsis, beim Umlauf von Planeten um die Sonne Perihel und Aphel:
Numerische Exzentrizität für Ellipsen, inkl. Kreis als Grenzfall:
Einige Zusammenhänge:
 \, a )
 )
Umlaufdauer bzw. Periode T für 360°:
}{a^3}} )
Radius des Orbits als Funktion des Winkels theta; theta wird auch wahre Anomalie genannt:
 = \frac{p}{1 + e \, \cos\theta} = \frac{(1 - e^2) \, a}{1 + e \, \cos\theta} )
Bewegungsgleichung für den Winkel; entspricht der Drehimpulserhaltung
^2} = \frac{\Omega}{(1-e^2)^{3/2}} \, dt )
Möglichkeiten zur Lösung der Bewegungsgleichung:
1) numerische Lösung der DGL (z.B. Python)
2) numerische Integration (z.B. Python)
3) analytische Integration (wolfram alpha findet eine zunächst komplexe, wenig handhabbare Lösung; ich bin noch dran)
Im folgenden betrachte ich die Keplergleichung. Dazu benötigen wir die mittlere Anomalie  und die exzentrische Anomalie psi. Den Zusammenhang zwischen beiden liefert die sogenannte Keplergleichung:
Zuletzt noch der Zusammenhang mit der wahren Anomalie, also dem gesuchten Winkel theta:
4.a) numerische Invertierung der Keplergleichung
4.b) Kontraktion
Die Keplergleichung definiert eine kontrahierende Abbildung, d.h. die Iteration
konvergiert (für genügend kleines e extrem schnell) gegen einen Fixpunkt, der eine eindeutige Lösung liefert.
4.c) Reihenentwicklung
Die Lösung für die wahre Anomalie, d.h. den Winkel theta, als Funktion der mittleren Anomalie M und damit letztlich der Zeit t:
 = \Omega t + 2 \cdot \sum_{n=1}^\infty \frac{1}{n} \left[J_n(ne) + \sum_{p=1}^\infty \beta^p \left[J_{n-p}(ne) + J_{n+p}(ne)\right] \right] \, \sin(n\Omega t) \\
<br />
\simeq \Omega t + \left( 2e - \frac{1}{4}e^3 \right) \, \sin(\Omega t) + \frac{5}{4}e^2 \, \sin(2 \Omega t) + \frac{13}{12} e^3 \, \sin(3 \Omega t) + \mathcal{O}(4) )
mit den Besselfunktionen erster Art für ganzzahliges n
 = \frac{1}{\pi} \int_0^\pi dt \, \cos(nt - x \, \sin t) )
 = (-)^n \, J_n(x))
sowie
Höhere Ordnungen hier:
https://en.wikipedia.org/wiki/Equation_of_the_center
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 22. Nov 2023 07:46, insgesamt 8-mal bearbeitet |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 21. Nov 2023 17:43 Titel: |
|
|
Hallo TomS , das sieht sehr beeindruckend aus. Jetzt kann ich mir ungefähr vorstellen, wie es ist, wenn ich jemanden etwas in JavaScript oder PHP als Lösung seines Problems vorschlage, der davon keine Ahnung hat.
Dieser Wert "Orbital eccentricity" kommt mir mittlerweile bekannt vor. Der wurde wohl in einem der Skripte auf Github verwendet, die ich durchgeschaut habe. Hast du da auch mal geschaut? Eventuell hat die gesuchte Formel schon jemand programmiert. Da gibt es auch viel in Python.
Bei "Maximum equation of the center" verstehe ich das "Center" nicht. Ansonsten scheint es den Werten nach so, dass die EOT der Erde um die Sonne relevant ist mit bis zu 1,9°.
Beim Erstellen der Formel sollte der Begriff Toleranz kein Fremdwort sein. Also Toleranz ist erlaubt, bzw. sollte in einem den Umständen entsprechenden (Rechenleistung/Schnelligkeit) Aufwand/Ergebnis-Verhältnis stehen. Vorgesehen ist eine Berechnung per JavaScript, also im Browser.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 21. Nov 2023 18:18 Titel: |
|
|
Hi, danke, aber das ist einfach nur Wikipedia lesen und zusammen schreiben ;-)
Bin gerade dabei, zwei Methoden zu implementieren. Sieht gut aus, die Konsistenzprüfung ist etwas tricky, da die erwarteten Abweichungen ohnehin sehr klein sind.
Ich bin mir ziemlich sicher, dass du fertigen Code auf GitHub findest; ich bin mir aber auch ziemlich sicher, dass es dauern wird, bis du ihn verstehst.
Der Kern einer Lösungsmethode sind immer nur wenige Zeilen Python-Code! Natürlich muss man da noch einiges drumherum bauen. An eine Lösung im Browser glaube ich ehrlich gesagt nicht. Wenn, dann wäre es die allerletzte Methode mit der Reihenentwicklung in e, evtl. kann man auch die Keplergleichung durch Iteration lösen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 21. Nov 2023 18:41 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | An eine Lösung im Browser glaube ich ehrlich gesagt nicht. |
Das kommt darauf an, wie genau das Ganze sein soll. Das konnte ich bisher noch nicht so richtig erkennen.
|
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 21. Nov 2023 18:55 Titel: |
|
|
Stimmt schon. Manchmal ist es schneller etwas neu zu schreiben als es zu suchen. Nicht so vorteilhaft ist, dass auf Github meist nur fertige Softwares angeboten werden, in denen das gesuchte implementiert ist. Dann ist es meist sehr aufwendig dieses zu extrahieren. Das ging mir bei der Sonnen-EOT-Formel ähnlich. Das war noch zu meiner Anfangszeit mit JavaScript und PHP. Es gibt aber auch nützliche Softwares (Skripte), die keine Fertiglösung in dem Sinne sind, dass sie ein fertiges Produkt sind, sondern die wie eine Rechenmaschine konstruiert sind, die verschiedene einzelne Werte ausgeben. Sowas gibt es für den Mond. Also nichts fertiges, sondern nur eine Engine zum Weiterverwenden. Input - Output. Das ist sehr praktisch.
Bisher habe ich auch nichts passendes gefunden, wobei mir etwas die Kenntnis fehlt wonach gesucht werden müsste. Es gibt bereits einiges zur Equation der Erde um die Sonne, allerdings mit anderem Schwerpunkt/Ziel. Wie die aktuelle Geschwindigkeit der Erde. Oder die Position (x, y, z) im Sonnen/Planetensystem. Oder den aktuellen G-Wert (Gravitation). Und einiges mehr.
|
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 21. Nov 2023 19:31 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | An eine Lösung im Browser glaube ich ehrlich gesagt nicht. |
Das kommt darauf an, wie genau das Ganze sein soll. Das konnte ich bisher noch nicht so richtig erkennen. |
Wie schon geschrieben sind Toleranzen erlaubt.
| Code: | Aktuelles tropisches Jahr: 31556925 Sekunden.
0,001° = 0° 0' 3,6'' = 87,658 Sekunden = 1,46 Minuten
1 Minute = 60 Sekunden = 0,0006844773° = 0° 0' 2,5'' |
Das wäre eine tolerierbare Toleranz. ±5 Minuten sind OK. ±10 Minuten wären auch noch OK. ±1 Minute wäre optimal.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 21. Nov 2023 19:41 Titel: |
|
|
| sembel hat Folgendes geschrieben: | | Das wäre eine tolerierbare Toleranz. ±5 Minuten sind OK. ±10 Minuten wären auch noch OK. ±1 Minute wäre optimal. |
Das wäre dann ein Fehler in der 7. von insgesamt 16 signifikanten Stellen. Das sollte machbar sein.
Zuletzt bearbeitet von DrStupid am 21. Nov 2023 19:57, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 21. Nov 2023 19:49 Titel: |
|
|
Hallo!
Wenn du tatsächlich vernünftig wiederverwendbare Software suchst, dann müsstest du wohl in Fach-Foren nach Astronomie-Libraries fragen. Die gibt es ganz sicher. Wie groß der Aufwand ist, diese tatsächlich zu verstehen, kann ich nicht beurteilen. Software, die ich aus der Physik kenne, ist meist sehr flexibel anpassbar, d.h. aber auch, man muss die gesamte Parametrierung verstehen.
Die von mir oben zusammen gestellten Gleichungen sollten der Startpunkt für deine Fragen sein.
Das zweite ist deine Forderung nach Javascript beziehungsweise Software im Browser. Genau das ist üblicherweise für professionelle Software nicht das Ziel. Die Software läuft zumeist auf Linux/Knoten, gerne auch verteilt, kann ich aber für Astronomie nicht wirklich beurteilen.
Ich kann gerne mein Script hier einstellen, die zwei oder drei numerischen Funktionen sind gut dokumentiert, damit könntest du nach entsprechender Software für Javascript o.ä. suchen.
Das alles gilt für die Lösung des Keplerproblems.
Wenn du allerdings doch in Richtung der Zeitgleichungen gehen möchtest, Einbeziehung der Erdrotation, also Lösung dreidimensionaler Probleme, Berücksichtigung von Schwankungen aufgrund des Mondes und anderer Planeten, dann ist der bisherige Weg eine Sackgasse. Natürlich könntest du mein Skript sukzessive erweitern, ich halte den Aufwand allerdings für extrem groß, zumal dir niemand die Beziehung zwischen Gleichungen und Software haarklein erklären wird; dann müsstest du wirklich auf die Suche nach fix und fertiger Software gehen – das wäre eine völlig andere Baustelle.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 21. Nov 2023 19:59 Titel: |
|
|
Ein Punkt zu den Fehlern: das beginnt schon mit zuverlässigen Parameterwerten.
Für die Bahnparameter der Erde – Halbachsen, Exzentrizität … – habe ich bisher außer in Wikipedia nichts frei verfügbares gefunden.
Das erste Problem ist schon mal, dass man deutlich voneinander abweichende Werte für das tropische Jahr und die Periode findet. Erklärung, Begründung, Korrekturen … Fehlanzeige.
Derartige systematische Fehler sind viel gravierender als das bisschen Numerik.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 21. Nov 2023 20:25 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Das erste Problem ist schon mal, dass man deutlich voneinander abweichende Werte für das tropische Jahr und die Periode findet. Erklärung, Begründung, Korrekturen … Fehlanzeige. |
Das könnte mit dem Einfluss der anderen Planeten zusammenhängen. Die Bahnparameter ändern sich ständig. Wikipedia ist nicht geeignet um aktuelle Werte zu liefern. Dafür gibt es andere Quellen. Werte für die Planeten in kartesischen oder Kugelkoordinaten gibt es beispielsweise bei https://ssp.imcce.fr/forms/ephemeris
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 21. Nov 2023 20:41 Titel: |
|
|
Naja, wenn sich die Wiki-Autoren die Mühe machen würden, vernünftige Referenzen anzuführen, dann wäre das ja kein Problem; aber einfach auf das Buch zu verweisen, das sie gerade lesen, ohne dass die Werte untereinander abgeglichen sind, ist natürlich…
Egal, danke, ich werde schon was finden.
Für die Funktion der Software ist das ja egal.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 21. Nov 2023 23:14 Titel: |
|
|
Ich wußte nicht, dass es so komplex ist. Andererseits soll es nicht all zu komplex werden.
Erdrotation und Mond-Einfluss sollen nicht mir rein. Das hatte ich weiter vorne schon erwähnt mit der Schlangenlinie des Erdorbits um die Sonne. Also der Einfluss weiterer Parameter ist meiner Ansicht nach zu gering, bzw. das Weglassen tolerierbar.
Den Winkel-Wert je Sekunde über die gemittelte Zeit von Wintersonnenwende zu Wintersonnenwende anhand bereits vorberechneter Werte habe ich ja bereits. Das ist ein einfacher Dreisatz. Da meiner Ansicht nach die Geschwindigkeitsschwankungen (gefühlt/geschätzt) einen relevanten Einfluss haben, wollte ich diese mit inkludieren. Deswegen die Frage hier nach einer EOT für den Erdorbit.
Die Frage nach so einer Formel wurde nicht zum ersten Mal gestellt, jedoch jedesmal mit anderer Intuition. Deswegen ist da (für mich) nichts brauchbares dabei:
runterscrollen:
https://www.researchgate.net/post/What-is-a-mathematical-way-to-calculate-the-Earths-position-on-its-orbit-in-terms-of-time
https://www.researchgate.net/post/How_can_I_calculate_the_Earths_orbit_or_what_is_the_equation_that_enable_us_know_its_velocity_vs_position_at_given_time
"I'd like to be able to get the z y x coordinates of the planet at any give time."
https://math.stackexchange.com/questions/4461111/what-is-the-equation-describing-earths-orbit-around-the-sun-in-3-dimensional-sp
"a. Find an equation of the Earth's orbit about the sun."
"b. With the given information, estimate Earth's speed around the sun in milers per hour."
https://math.stackexchange.com/questions/512989/equation-of-earths-orbit-around-sun-ellipse
"The eccentricity of the Earth’s orbit is currently about 0.01671022. Its semimajor axis is 1.00000011 AU."
https://www.nku.edu/~longa/classes/2010fall/mat227/days/labs/lab27/lab27.pdf
"Fitting the equation of Earth"
https://uploads-ssl.webflow.com/5ef2c10e4e52ca7f7c1bd820/5f8cdc3ae3d2d33fee6f48b0_A%20Model%20of%20Earth%27s%20Orbit.pdf
In diesem Video der Python Code leider nur im Video:
https://www.youtube.com/watch?v=dmVdNWnAY50
Der Weg über Fach-Foren bringt meinen Erfahrungen nach nichts. Viele nutzen bereits vorgefertigte Software und verweisen wenn dann wie Wikipedia auf Bücher.
Andererseits gibt es präzise Software, die solche Formeln/Gleichungen/Berechnungen inkludiert hat. Der Weg, eine passende Formel über diese zu finden, also von dieser zu exrahieren, ist zu aufwendig bis nicht möglich (kein Open Source).
Was die Umwandlung von Python zu JavaScript betrifft, da findet sich sicher eine Lösung. Die Sonnen-EOT-Formel habe ich in JavaScript und Java verwendet. Java - das Problem mit den Nachkommastellen.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 21. Nov 2023 23:29 Titel: |
|
|
| sembel hat Folgendes geschrieben: | | Ich wußte nicht, dass es so komplex ist. Andererseits soll es nicht all zu komplex werden. |
Es ist nicht komplex. Alles notwendige steht in meinem obigen Beitrag.
| sembel hat Folgendes geschrieben: | | Erdrotation und Mond-Einfluss sollen nicht mir rein. Das hatte ich weiter vorne schon erwähnt mit der Schlangenlinie des Erdorbits um die Sonne. Also der Einfluss weiterer Parameter ist meiner Ansicht nach zu gering, bzw. das Weglassen tolerierbar. |
Gut.
| sembel hat Folgendes geschrieben: | | Den Winkel-Wert je Sekunde über die gemittelte Zeit von Wintersonnenwende zu Wintersonnenwende anhand bereits vorberechneter Werte habe ich ja bereits. |
Das verstehe ich nicht.
| sembel hat Folgendes geschrieben: | | Da meiner Ansicht nach die Geschwindigkeitsschwankungen (gefühlt/geschätzt) einen relevanten Einfluss haben, wollte ich diese mit inkludieren. |
Die Schwankungen sind oben enthalten, jedoch sehr klein. Script und Plots kommen noch.
| sembel hat Folgendes geschrieben: | | Deswegen die Frage hier nach einer EOT für den Erdorbit. |
In der Physik sprechen wir einfach vom Orbit.
Keine Ahnung, warum das so schwierig sein soll. In der Wikipedia erscheint es halt etwas unübersichtlich, weil die Astronomen zig verschiedene Begriffe einführen. Ansonsten ist das Standard im Physikstudium.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
|
|
sembel
Anmeldungsdatum: 14.07.2019
Beiträge: 46
|
| sembel Verfasst am: 22. Nov 2023 00:05 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
| sembel hat Folgendes geschrieben: | | Den Winkel-Wert je Sekunde über die gemittelte Zeit von Wintersonnenwende zu Wintersonnenwende anhand bereits vorberechneter Werte habe ich ja bereits. |
Das verstehe ich nicht. |
Hier die Berechnung des gemittelten Winkelmaßes für die jeweils aktuelle Zeit mit bereits vorberechneter Werte für die Wintersonnenwenden.
JavaScript für die Browser Konsole:
| Code: | var ws_2022 = 1671659280;
var ws_2023 = 1703215620;
var ty = ws_2023 - ws_2022;
var timestamp = (new Date().getTime() / 1000);
var current = timestamp - ws_2022;
var angle = (current / ty) * 360;
angle; // Beispiel: 330.251016730076
|
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 22. Nov 2023 01:27 Titel: |
|
|
Ich verstehe jede Zeile des Scripts, aber der Sinn bleibt leider rätselhaft.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 22. Nov 2023 09:14 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Ich verstehe jede Zeile des Scripts, aber der Sinn bleibt leider rätselhaft. |
Das ist der Winkel für eine exakte Kreisbahn. Ich würde das mal als nullte Nährung bezeichnen.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 22. Nov 2023 11:52 Titel: |
|
|
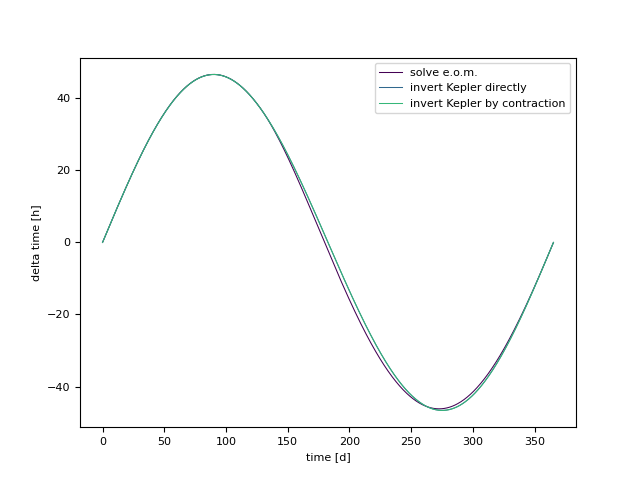
Anbei das erste Script zur Lösung des Problems (ich habe noch ein kleines Problem beim Handling der Winkel, d.h. Artefakte wie Sprünge um 2*pi, die ich rausrechnen muss; ist aber für eine Periode kein Problem). Aufgetragen ist jeweils die Schwankung um den mittleren Orbit, d.h. für e = 0, in Stunden.
Ich betrachte drei Methoden: die direkte Lösung der DGL für theta sowie zwei Methoden zur Lösung der Keplergleichung. Die drei Lösungen weichen minimal voneinander ab, die beiden letzten sind praktisch identisch.
Nicht plausibel erscheint mir die große Abweichung im Bereich von einigen zehn Stunden! Da dies von allen drei Methoden konsistent reproduziert wird, ist hier evtl. noch ein systematisches Problem verborgen.
| Code: | """ solution of the Kepler orbit: radius as function of the angle, ii) angle as function of time
Author: Tom
Date: 2023-11-21
"""
# imports --------------------
import numpy as np
import scipy.optimize as sci_opt
import scipy.integrate as sci_int
import matplotlib.pyplot as plt
plt.rc('font', size=8)
# constants --------------------
class OrbParams:
def __init__(self, ecc=0.0167086, a=149.598022960e9, period=365.256363004*24*3600): # wikipedia
self.ecc = ecc
self.a = a
self.period = 365.256363004 * 24 * 3600
self.b = np.sqrt(1 - self.ecc**2) * self.a
self.a = a
self.p = (1 - self.ecc**2) * self.ecc
self.om = 2 * np.pi / self.period
the_orb = OrbParams()
# geometry --------------------
def theta(psi, ecc):
''' returns the angle as a function of te eccentric anomaly psi; psi currently restricted to [0, 2*pi] '''
''' THERE'S STILL AN ISSUE WITH THE INTERVAL! '''
theta = 2 * np.arctan( np.sqrt((1+ecc)/(1-ecc)) * np.tan(psi/2))
theta = np.where(theta > 0.0, theta, theta+2*np.pi)
theta[0] = 0.0
return theta
# 1. numerical solution of the differential equation --------------------
def dot_theta(theta, Om, ecc):
''' returns the derivative of theta w.r.t. time '''
return (Om / (1 - ecc**2)**(3/2)) * (1 + ecc * np.cos(theta))**2
def theta_eom(t, state, Om, ecc):
''' defines the e.o.m. for theta '''
theta = state[0]
d_theta = dot_theta(theta, Om, ecc)
return [d_theta]
def integrate_theta_eom(t, Om, ecc):
''' solves the e.o.m. for theta '''
sol = sci_int.solve_ivp(fun=theta_eom, t_span=[t[0], t[-1]], y0=[0.0], t_eval=t, args=(Om, ecc), method='RK45')
return sol.y[0]
# 2. numerical solution via contraction --------------------
def Kepler_eq(psi, t, Om, ecc):
''' defines Kepler eq. as psi - e * sin(psi) - Omega * t = 0 '''
return psi - ecc * np.sin(psi) - Om * t
def invert_Kepler_eq(t, Om, ecc):
''' solution via root finding for Kepler eq. '''
sol = sci_opt.root(fun=Kepler_eq, x0=Om*t, args=(t, Om, ecc))
psi = sol.x
return theta(psi, ecc)
# 3. numerical solution via contraction --------------------
def Kepler_eq_c(psi, t, Om, ecc):
''' defines Kepler eq. as psi = Omega * t + e * sin(psi) '''
return Om * t + ecc * np.sin(psi)
def Kepler_eq_iter(t, Om, ecc):
''' solution via contraction of psi = Omega * t + e * sin(psi) '''
Om_t = Om * t
psi = Om_t
for n in range(0, 5):
psi = Om_t + ecc * np.sin(psi)
return psi
def contract_Kepler_eq(t, Om, ecc):
psi = Kepler_eq_iter(t, Om, ecc)
return theta(psi, ecc)
# some helper functions --------------------
def plot(t_arr, func_arrs, texts):
cmap = plt.get_cmap('viridis')
plt.xlabel('time [d]')
plt.ylabel('delta time [h]')
for idx, (func, text) in enumerate(zip(func_arrs, texts)):
c = cmap(idx / (len(func_arrs)))
plt.plot(t_arr/(24*3600), func / 3600, lw=0.75, color=c, label=text)
plt.legend()
plt.show()
return
# driver code --------------------
t_arr = np.linspace(0.0, the_orb.period, 1000)
twopi_arr = np.linspace(0.0, 2*np.pi, 1000)
# 1.
theta_arr_1 = integrate_theta_eom(t_arr, the_orb.om, the_orb.ecc)
delta_theta_arr_1 = theta_arr_1 - twopi_arr
delta_t_arr_1 = delta_theta_arr_1 / the_orb.om
# 2.
theta_arr_2 = invert_Kepler_eq(t_arr, the_orb.om, the_orb.ecc)
delta_theta_arr_2 = theta_arr_2 - twopi_arr
delta_t_arr_2 = delta_theta_arr_2 / the_orb.om
# 3.
theta_arr_3 = contract_Kepler_eq(t_arr, the_orb.om, the_orb.ecc)
delta_theta_arr_3 = theta_arr_3 - twopi_arr
delta_t_arr_3 = delta_theta_arr_3 / the_orb.om
plot(t_arr, [delta_t_arr_1, delta_t_arr_2, delta_t_arr_3], ['solve e.o.m.', 'invert Kepler directly', 'invert Kepler by contraction']) |
| Beschreibung: |
| deviation of real Kepler orbit from mean orbit for e=0 in hours |
|
| Dateigröße: |
27.25 KB |
| Angeschaut: |
3405 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 22. Nov 2023 13:00, insgesamt 5-mal bearbeitet |
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
| Nils Hoppenstedt Verfasst am: 22. Nov 2023 12:06 Titel: |
|
|
Hi,
Hier noch ein alternativer Lösungsvorschlag durch direktes Integrieren der Newtonschen Bewegungsgleichungen:
| Code: |
import matplotlib.pyplot as plt
import numpy as np
# Constants
G = 6.67430e-11 # Gravitational constant (m^3 kg^-1 s^-2)
m_sun = 1.989e30 # Mass of the Sun (kg)
m_earth = 5.972e24 # Mass of the Earth (kg)
au = 149.6e9 # Astronomical Unit (m)
# Initial conditions
initial_position = np.array([au, 0.0]) # Initial position of Earth (m)
initial_velocity = np.array([0.0, 29783.0]) # Initial velocity of Earth (m/s)
initial_time = 0.0 # Initial time (s)
# Simulation parameters
total_time = 365 * 24 * 60 * 60 # Total simulation time (1 year in seconds)
time_step = 60 * 60 # Time step (1 hour in seconds)
# Function to calculate gravitational force
def gravitational_force(position):
r = np.linalg.norm(position)
force_magnitude = G * (m_sun * m_earth) / r**2
force_direction = -position / r # Force direction is opposite to position vector
force = force_magnitude * force_direction
return force
# Function to perform numerical integration using Euler's method
def simulate_orbit(initial_position, initial_velocity, initial_time, total_time, time_step):
positions = [initial_position]
velocities = [initial_velocity]
times = [initial_time]
position = initial_position
velocity = initial_velocity
time = initial_time
while time < total_time:
force = gravitational_force(position)
acceleration = force / m_earth
# Update velocity and position using Euler's method
velocity = velocity + acceleration * time_step
position = position + velocity * time_step
# Update time
time = time + time_step
# Save data for plotting
positions.append(position.copy())
velocities.append(velocity.copy())
times.append(time)
return np.array(positions), np.array(velocities), np.array(times)
# Run simulation
positions, velocities, times = simulate_orbit(initial_position, initial_velocity, initial_time, total_time, time_step)
# Plot the orbit
plt.figure(figsize=(8, 8))
plt.plot(positions[:, 0], positions[:, 1])
plt.title("Earth's Orbit Around the Sun")
plt.xlabel("X Position (meters)")
plt.ylabel("Y Position (meters)")
plt.axis('equal')
plt.show()
|
Viele Grüße,
Nils
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 22. Nov 2023 12:22 Titel: |
|
|
👍
Tust du mir den Gefallen und plottest den Winkel theta, in der Einheit Stunden? Evtl. habe ich in der folgenden Argumentation einen Denkfehler:
 = \theta(t) - \Omega t)
Und damit folgt, dass die Erde aufgrund des elliptischen Orbits teilweise um einige 10 Stunden falsch geht. Was ich irgendwie nicht glauben kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
