| Autor |
Nachricht |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Apr 2009 09:54 Titel: Absturz der Erde franz Verfasst am: 06. Apr 2009 09:54 Titel: Absturz der Erde |
 |
|
Hallo!
Knobelaufgabe: Wie lange würde die - in ihrer Bahnbewegung gestoppte - Erde zur Sonne fallen?
mfG F.
PS Sollte diese Frage hier schon (sinngemäß) geklärt sein, bitte ich um freundliche Löschung. Habe jedoch nichts passendes gefunden.
|
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 06. Apr 2009 17:06 Titel: pressure Verfasst am: 06. Apr 2009 17:06 Titel: |
 |
|
|
Kennst du das Gravitationsgesetz ?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Apr 2009 17:30 Titel: franz Verfasst am: 06. Apr 2009 17:30 Titel: |
 |
|
Das Stichwort "Knobelaufgabe" deutet an, daß ich die Lösung kenne.
Tschüß
F
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 06. Apr 2009 17:57 Titel: para Verfasst am: 06. Apr 2009 17:57 Titel: |
 |
|
Es müsste sogar gehen, ohne direkt das Gravitationsgesetz zu bemühen (was wohl in einer DGL enden würde). :)
_________________
Formeln mit LaTeX |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Apr 2009 22:50 Titel: franz Verfasst am: 06. Apr 2009 22:50 Titel: |
 |
|
Ja, es gibt (leider!) auch eine billige Lösung. :-(
F.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 06. Apr 2009 23:17 Titel: TomS Verfasst am: 06. Apr 2009 23:17 Titel: |
 |
|
Ich hab's wie folgt gerechnet:
F = ma
F ist die Anziehungskraft der Sonne ~1/r²
a die Beschleunigung, also d²r/dt²
Daraus ergibt sich eine einfache DGL in r(t)
Problem ist, dass F(r) bei r=0 singulär ist!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 07. Apr 2009 00:00 Titel: franz Verfasst am: 07. Apr 2009 00:00 Titel: |
 |
|
Wieso r = 0?
F.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 07. Apr 2009 00:13 Titel: TomS Verfasst am: 07. Apr 2009 00:13 Titel: |
 |
|
OK, wenn wir die Erde nur bis auf die Sonnenoberfläche stürzen lassen, dann stört uns r=0 natürlich nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 07. Apr 2009 07:18 Titel: franz Verfasst am: 07. Apr 2009 07:18 Titel: |
 |
|
Hallo Tom, ich denke, daß man die Sonnenoberfläche als Ziel der Reise akzeptieren kann. Bleibt, wie von Dir angeschrieben, a(r).
mfG, F.
|
|
 |
Herbststurm

Anmeldungsdatum: 05.09.2008
Beiträge: 412
Wohnort: Freiburg i. Brsg.
|
 Herbststurm Verfasst am: 07. Apr 2009 14:37 Titel: Herbststurm Verfasst am: 07. Apr 2009 14:37 Titel: |
 |
|
| franz hat Folgendes geschrieben: | Ja, es gibt (leider!) auch eine billige Lösung. :-(
F. |
Extrem dämlicher Satz... 
|
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 07. Apr 2009 14:52 Titel: Gargy Verfasst am: 07. Apr 2009 14:52 Titel: |
 |
|
@herbststrum: Naja, das ist wohl Ansichtssache... aber die Wortwahl 
_________________
Ich habe ins Blaue geschossen und ins Schwarze getroffen - Friedrich Dürrenmatt
Zuletzt bearbeitet von Gargy am 07. Apr 2009 14:52, insgesamt einmal bearbeitet |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 07. Apr 2009 14:52 Titel: franz Verfasst am: 07. Apr 2009 14:52 Titel: |
 |
|
Habe ich Deinen Ehrgeiz dadurch gebremst? 
Wie immer
mit freundlichen Grüßen
Franz
|
|
 |
Herbststurm

Anmeldungsdatum: 05.09.2008
Beiträge: 412
Wohnort: Freiburg i. Brsg.
|
 Herbststurm Verfasst am: 07. Apr 2009 15:01 Titel: Herbststurm Verfasst am: 07. Apr 2009 15:01 Titel: |
 |
|
| Gargy hat Folgendes geschrieben: | @herbststrum: Naja, das ist wohl Ansichtssache... aber die Wortwahl  |
Nö, das ist keine Ansichtssache. Da gibt es auch keinen Spielraum indem man sich bewegen kann. Die Aussage ist einfach gewaltiger Unfug. Und klare Worte vermeiden Verständigungsprobleme 
Leider billige Lösungen.... Das ist absolut Anti-Physik Wann immer ein Problem lösbar ist - ob eindeutig oder nicht sei mal dahingestellt - dann ist die einfachste Lösung immer die Beste.
Was Franz gemeint haben könnte (wissen wir ja nicht, falls er das gemeint hat, dann ist es völlig falsch formuliert gewesen) und zwar, dass man etwas Theoretisch untersucht, dies aber dann weiter und weiter bearbeitet, bis letzlich wieder dieser einfachste Weg da ist. Wie das konkret aussieht hängt natürlich von der Problemstellung ab.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 07. Apr 2009 18:24 Titel: franz Verfasst am: 07. Apr 2009 18:24 Titel: |
 |
|
Wenn es denn der Wahrheitsfindung dient: Einverstanden, ich bin ein böser Mensch. Und werde außerdem ab sofort hier die Klappe halten. :-)
Franz
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 07. Apr 2009 19:31 Titel: schnudl Verfasst am: 07. Apr 2009 19:31 Titel: |
 |
|
omannomannomannomann...
könnte es Franz evtl. ironisch gemeint haben? Es war ja von Anfang an klar, dass er uns eine Knobelei aufgibt. Und da kann es schon ein ordentliches Aha Erlebnis geben, wenn man in Anbetracht einer genial einfachen Lösung dann sagen muss: "leider bin ich nicht draufgekommen dass es so billig geht...". Man muss ja nicht jeden Wortlaut gleich auf die Goldwaage legen und so tun, als handle es sich um einen Artikel in PhysRev.

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Gast
|
 Gast Verfasst am: 08. Apr 2009 09:21 Titel: Gast Verfasst am: 08. Apr 2009 09:21 Titel: |
 |
|
|
Eine grobe Rechnung zeigt, dass die Geschwindigkeit an der Sonnenoberfläche etwa 500km/s beträgt. Das ist relativistisch wenig, also wird das 3. Keplersche Gesetz immer noch gelten, wonach die Umlaufzeit nur von der großen Achse der Ellipse abhängt --> Fallzeit = 1/4 Jahr
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 13:02 Titel: as_string Verfasst am: 08. Apr 2009 13:02 Titel: |
 |
|
| Anonymous hat Folgendes geschrieben: | | Eine grobe Rechnung zeigt, dass die Geschwindigkeit an der Sonnenoberfläche etwa 500km/s beträgt. Das ist relativistisch wenig, also wird das 3. Keplersche Gesetz immer noch gelten, wonach die Umlaufzeit nur von der großen Achse der Ellipse abhängt --> Fallzeit = 1/4 Jahr |
Ich glaube, Du machst da einen Fehler: Der Zentralkörper muss in einem der beiden Brennpunkte der Ellipse liegen, nicht in ihrem Mittelpunkt.
Gruß
Marco
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 08. Apr 2009 13:04 Titel: TomS Verfasst am: 08. Apr 2009 13:04 Titel: |
 |
|
Ich hab versucht, die DGL zu lösen und komme auf ca. 24 Tage
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 13:07 Titel: as_string Verfasst am: 08. Apr 2009 13:07 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ich hab versucht, die DGL zu lösen und komme auf ca. 24 Tage |
Ich komme irgendwie auf das Doppelte... Oh mann, diese blöden Konstanten immer.
Über Kepler komme ich auf 64,6 Tage. Ich glaube, das muss ich nochmal nachrechnen.
Gruß
Marco
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 08. Apr 2009 14:38 Titel: TomS Verfasst am: 08. Apr 2009 14:38 Titel: |
 |
|
Mein Ansatz ist  mit mit  und und

Ich mache den Ansatz
=r_{0}\left(\frac{t}{T}\right)^{z})
Einsetzen in die DGL liefert
r_{0}T^{-z}t^{z-2})
Zunächst bestimmt man

Dann kann man zwischen den beiden Konstanten die Beziehung

herstellen.
Die Lösung der DGL lautet
=r_{0}\left(\frac{t}{T}\right)^{2/3})
Für den Fall ins Zentrum muss man negative Zeiten annehmen; das Zentrum wird dann erreicht für die Zeit  . .
Zum Zeitpunkt 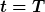 hat man den Abstand hat man den Abstand =r_0) . .
Löst man die obige Gleichung nach 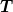 auf, so erhält man auf, so erhält man

(Lästiges) Einsetzen der Zahlenwerte liefert (wenn ich mich nicht verrechnet habe) ca. 24 Tage für den Sturz ins Zentrum (wobei nahe dem Zentrum die Gleichung natürlich streng genommen nicht mehr gilt, da hier die Geschwindigkeit divergiert).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 08. Apr 2009 15:01, insgesamt einmal bearbeitet |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 14:51 Titel: as_string Verfasst am: 08. Apr 2009 14:51 Titel: |
 |
|
Hallo!
Ich habs etwas anders gerechnet. Ich bin mir nicht sicher, ob man mit diesem Ansatz anfangen kann. Ich meine, dass der nicht allgemein genug ist. Muss ich mir aber erst noch anschauen. Eigentlich sollten zwei Konstanten ja schon ausreichen, wenn es eine DGL zweiter Ordnung ist, denke ich. Mmh...
Ich habe zumindest als Endergebnis etwas sehr ähnliches raus:
 <--- Tippfehler: da müsste <--- Tippfehler: da müsste  sein sein
Ich bekam da nach lästigem Einsetzen dann etwa 47,5 Tage raus, allerdings stimmt das dann wahrscheinlich auch nicht wirklich.
Später muss ich das alles nochmal genau anschauen.
Gruß
Marco
Zuletzt bearbeitet von as_string am 08. Apr 2009 16:52, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 08. Apr 2009 15:20 Titel: TomS Verfasst am: 08. Apr 2009 15:20 Titel: |
 |
|
Deine Formel sieht sehr ähnlich aus wie meine; ich bevorzuge (ohne Rechnung) auf den ersten Blick meine, weil darin das Quadrat der Zeit und der Kubus des Radius vorkommt - was wieder zu Kepler führt.
Ich kann mich irren.
Bzgl. der zwei Konstanten: ich habe sie zunächst nur eingeführt, damit ich die Dimension richtig hinbekomme. Zu deiner Argumentation mit der DGL zweiter Ordnung: ich bin mir nicht sicher, ob das hier so zutrifft, denn es handelt sich um eine nichtlineare DGL, die gesuchte Funktion r(t) kommt quadratisch vor!
Ich kann mich auch da irren :-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast
|
 Gast Verfasst am: 08. Apr 2009 15:23 Titel: Gast Verfasst am: 08. Apr 2009 15:23 Titel: |
 |
|
@as_string
| Zitat: | | Über Kepler komme ich auf 64,6 Tage. Ich glaube, das muss ich nochmal nachrechnen. |
Das stimmt, wie immer du es auch gerechnet hast.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 16:49 Titel: as_string Verfasst am: 08. Apr 2009 16:49 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Deine Formel sieht sehr ähnlich aus wie meine; ich bevorzuge (ohne Rechnung) auf den ersten Blick meine, weil darin das Quadrat der Zeit und der Kubus des Radius vorkommt - was wieder zu Kepler führt. |
Ah, sorry: Das ist ein Tippfehler. Ich habe da auch hoch drei stehen!
| Zitat: | | Das stimmt, wie immer du es auch gerechnet hast. |
Naja mit Kepler: Wenn Du Dir eine Kepler-Ellipse anschaust, die sehr flach ist: Die beiden Brennpunkte von Ellipsen wandern immer weiter nach außen an den Rand, je flacher die Ellipse ist. Da die Sonne in einem der Brennpunkte sein muss, sieht die "Ellipse" so aus, dass die Erde auf die Sonne zu fliegt und dann wieder in die selbe Richtung zurück fliegen würde. Die große Halbachse ist also gerade halb so groß, wie der Radius der Erdbahn. Außerdem ist die Bahn bis zum Sturz in die Sonne zur Hälfte durchflogen. Man hat also für die Umlaufzeiten:
^2 = \left(\frac{a_2}{a_1}\right)^3)
^{3/2}T_1)
Dabei ist T2 die Umlaufzeit auf der neuen, sehr flachen "Ellipse" und a2/a1 = ½. Die Hälfte der Umlaufzeit T2 ist die gesuchte Zeit bis Kollision:

Meine DGl-Lösung muss ich erst nochmal genau anschauen. Da ist der Wurm drin, so viel steht fest...
Gruß
Marco
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 08. Apr 2009 17:24 Titel: TomS Verfasst am: 08. Apr 2009 17:24 Titel: |
 |
|
Die beiden Rechenwege sind nicht äquivalent!
Gefragt ist doch der Fall der Erde in die Sonne. Damit handelt es sich nicht um eine flache Ellipse, sondern um eine nahezu kreisförmige Ellipse. D.h. man kann für kleine und große Halbachse näherungsweise den mittleren Bahnradius einsetzen.
Im Falle der Kepler-Bahn mit einer sehr flachen Ellipse gilt aber eben nicht "Die Hälfte der Umlaufzeit T2 ist die gesuchte Zeit bis Kollision"!
Im Falle der flachen Ellipse ist die Geschwindigkeit im sonnennahen Teil der Bahn wesentlich größer als im sonnenfernen Teil. D.h. dass in der Hälfte eines "Jahres" wesentlich mehr als 50% der Bahn zurückgelegt werden. Setze ich nun die obige Gleichung (ohne Kepler) an, so hängt die Zeit bis zum Sturz in die Sonne ausschließlich von der Entfernen der Erde von der Sonne ab. D.h. dass aber eben im Keplerfall mit flacher Ellipse die verschiedenen Punkte auf der Bahnkurve nicht mehr gleichberechtigt sind, da eben unterschiedliche Bahnradien vorliegen.
Die Aufgabenstellung lautet "Wie lange würde die - in ihrer Bahnbewegung gestoppte - Erde zur Sonne fallen?" Ich denke nicht, dass der Keplerfall der gestoppten Bahnbewegung entspricht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 17:30 Titel: as_string Verfasst am: 08. Apr 2009 17:30 Titel: |
 |
|
So, zu der DGl:
Man hat also das hier nach dem Newton-Ansatz:

So eine DGl der Form  = 0) kann man i. A. lösen, indem man mit kann man i. A. lösen, indem man mit 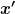 multipliziert und dann integriert. In diesem Fall bekommt man also: multipliziert und dann integriert. In diesem Fall bekommt man also:


Darauf kann man auch gleich kommen, wenn man einen Energie-Erhaltungs-Ansatz nimmt. Dabei wird auch klar, wie die Konstante sein muss: Im Abstand r=r0 ist die Geschwindigkeit 0, also muss die rechte Seite zu:
)
werden, wie man es später auch mit den Zwangsbedingungen sicher raus finden könnte.
Diese Gleichung ist separabel. Allerdings habe ich jetzt ein Problem: Ich muss erst die Wurzel ziehen und so weiter, um letztendlich auf:
\right)^{-1/2}\,\mathrm{d}r = \mathrm{d}t)
zu kommen. Wenn ich das in den "Wolfram Integrator" eintippe, bekomme ich was ziemlich hässliches mit 1/tan(...) und so weiter geliefert. Das hatte ich bei meiner bisherigen Rechnung falsch. Kann gut sein, dass man damit dann auch auf das Ergebnis kommen würde, wie mit Kepler. Ich habe hier jetzt erstmal aufgehört.
Bei Deiner Lösung der DGl gefallen mir ein paar Sachen nicht. Z. B. weiß ich nicht, wie man die Randbedingungen unterbringen sollte. Z. B. ist bei Dir r(t=0) ja immer 0, egal zu was ich r0 bestimme. Erst bei t=T wird r(r=T) = r0. Außerdem wird mit größerem t der Radius bei Dir immer größer, oder? Irgendwas ist da merkwürdig... Kein sein, dass die DGL damit gelöst wird, aber es ist sicher nicht die allgemeine Lösung und für diese Randbedingungen offensichtlich nicht die richtige, so weit ich das erkennen kann, zumindest.
Gruß
Marco
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 17:40 Titel: as_string Verfasst am: 08. Apr 2009 17:40 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Die beiden Rechenwege sind nicht äquivalent!
Gefragt ist doch der Fall der Erde in die Sonne. Damit handelt es sich nicht um eine flache Ellipse, sondern um eine nahezu kreisförmige Ellipse. D.h. man kann für kleine und große Halbachse näherungsweise den mittleren Bahnradius einsetzen.
Im Falle der Kepler-Bahn mit einer sehr flachen Ellipse gilt aber eben nicht "Die Hälfte der Umlaufzeit T2 ist die gesuchte Zeit bis Kollision"!
Im Falle der flachen Ellipse ist die Geschwindigkeit im sonnennahen Teil der Bahn wesentlich größer als im sonnenfernen Teil. D.h. dass in der Hälfte eines "Jahres" wesentlich mehr als 50% der Bahn zurückgelegt werden. Setze ich nun die obige Gleichung (ohne Kepler) an, so hängt die Zeit bis zum Sturz in die Sonne ausschließlich von der Entfernen der Erde von der Sonne ab. D.h. dass aber eben im Keplerfall mit flacher Ellipse die verschiedenen Punkte auf der Bahnkurve nicht mehr gleichberechtigt sind, da eben unterschiedliche Bahnradien vorliegen.
Die Aufgabenstellung lautet "Wie lange würde die - in ihrer Bahnbewegung gestoppte - Erde zur Sonne fallen?" Ich denke nicht, dass der Keplerfall der gestoppten Bahnbewegung entspricht. |
Irgendwie reden wir aneinander anscheinend vorbei...
Also: Angenommen die Erde und die Sonne wären punktförmig. Man kann sich ja jetzt eine Kepler-Ellipse vorstellen, die sehr sehr flach ist, so dass der eine Brennpunkt, in dem dann die Sonne wäre (Zentralkörper muss im Brennpunkt sein), in der einen "Spitze" dieser Ellipse wäre. Die Erde würde dann eine Fallbewegung (fast) direkt auf die Sonne zu machen, dann ganz schnell und ganz knapp um die Sonne einen Bogen machen und dann wieder zurück fliegen. Im Extremfall wird diese sehr flache Ellipse zu einer Geraden, wie in der Aufgabe verlangt. Und für die Bewegung vom weitest entfernten Punkt (dort, wo die ruhende Erde losgelassen wird) bis zur Sonne dauert natürlich genau so lange, wie der Weg zurück von der Sonne bis zum weitest entfernten Punkt. Im Beispiel wird dieser Weg natürlich nicht mehr zurück gelegt, weil die Erde dann schon in die Sonne gestürzt ist. Aber das ändert ja nichts an der Kepler-Ellipse vor der Kollision! Für die wird immer noch die halbe Umlaufszeit benötigt, auch wenn die zweite Hälfte gar nicht mehr durchflogen wird.
Die große Halbachse bei der neuen, sehr sehr flachen Ellipse ist natürlich gerade halb so groß, wie die große Halbachse der original-Kepler-Ellipse des echten Erdumlaufs, der natürlich annähernd kreisförmig ist. Und so komme ich auf meinen Ansatz (der ja auch richtig zu sein scheint...)
Überleg Dir das nochmal. Ich glaube, Du hast mich einfach nicht richtig verstanden. Vielleicht habe ich es auch nicht klar ausgedrückt, was ich gemacht habe. Ich weiß im Moment aber nicht, wie ich es besser beschreiben kann, leider.
Gruß
Marco
//Edit: Nochmal, das hier verstehe ich nicht:
| TomS hat Folgendes geschrieben: | | Gefragt ist doch der Fall der Erde in die Sonne. Damit handelt es sich nicht um eine flache Ellipse, sondern um eine nahezu kreisförmige Ellipse. |
Ein gerader Fall der Erde in die Sonne ist doch wohl die flachste Ellipse, die man sich vorstellen kann! Auf einer Kreisbahn ist die Erde ja (fast) jetzt schon, und mir ist nicht bekannt, dass sie alle paar Tage/Monate in die Sonne stürzen würde...
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 08. Apr 2009 18:04 Titel: as_string Verfasst am: 08. Apr 2009 18:04 Titel: |
 |
|
Nochmal zur Kepler-Lösung: Wenn man für die Umlaufzeit der Erde (genähert als Kreisbahn) nimmt nimmt:

(was ja einem Jahr entsprechen sollte)
Dann ergäbe sich für T:

Das sieht mir persönlich schon danach aus, als ob das die richtige Lösung der DGl sein könnte, wenn man die Anfangsbedingungen richtig behandelt hat...
Gruß
Marco
|
|
 |
Gast
|
 Gast Verfasst am: 08. Apr 2009 18:19 Titel: Gast Verfasst am: 08. Apr 2009 18:19 Titel: |
 |
|
Ich wollte mich auch mal dran versuchen und bin - wie ich jetzt feststellte - auf dem Weg von as_string gelandet.
Allerdings habe ich dann dummerweise bei der ersten Integration die Konstante verdaddelt (dämlicher Denkfehler, ich kam drauf, dass auf beiden Seiten eine Null steht - aber das ist ja Mist).
Im Endeffekt bin ich mit verlorener Konstante mittels Separation dann auf die Formel von TomS gekommen.
Vielleicht stimmt daher in seinem Ansatz auch irgendwas mit den Konstanten nicht.
Gruß
MI
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 08. Apr 2009 23:32 Titel: TomS Verfasst am: 08. Apr 2009 23:32 Titel: |
 |
|
Neuer Versuch, diesmal mittels der Energiegleichung

und der Anfangsbedingung

Umstellen liefert
)
Durch Trennung der Variablen erhält man für T (das ist die Zeit für den Sturz ins Zentrum) die Formel

Nun substituiert man

Damit kann man das Integral umformen zu

Für das Integral erhalte ich den Wert 
Damit lautet das Endresultat (leider anders als oben :-)

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 09. Apr 2009 08:49 Titel: schnudl Verfasst am: 09. Apr 2009 08:49 Titel: |
 |
|
diesen Ansatz habe ich auch probiert - nachdem ich das Integral aber in den Wolfram Integrator eingegeben hatte, war ich leider zu schnell entmutigt... Wahrscheinlich kann man den Ausdruck der dort geliefert wird entsprechend vereinfachen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Apr 2009 08:57 Titel: TomS Verfasst am: 09. Apr 2009 08:57 Titel: |
 |
|
Du kannst das selbst integrieren, indem du die Substitution

verwendest.
Außerdem musst du ja nur das bestimmte Integral berechnen, das macht der Integrator aber nicht - oder?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 09. Apr 2009 11:04 Titel: wishmoep Verfasst am: 09. Apr 2009 11:04 Titel: |
 |
|
Nur eine kurze Verständnisfrage zur Substitution; würde es nicht mehr Sinn machen mit x=sin² zu ersetzen?

Wenn ich jetzt gerade keinen Denkfehler habe, oder meintest du das sowieso TomS?
Denn das unbestimmte Integral vom Tangens ist ja hinreichend bekannt mit
\,\dd x = -\ln(|\cos x|) \;\;\;\;\;x\neq(2k+1)\cdot\frac{\pi}{2}\;;\;k\in\mathbb{Z})
Zuletzt bearbeitet von wishmoep am 09. Apr 2009 11:09, insgesamt einmal bearbeitet |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 09. Apr 2009 11:09 Titel: as_string Verfasst am: 09. Apr 2009 11:09 Titel: |
 |
|
Sehr schön! Dann kommt man ja tatsächlich auf die selben Ergebnisse, egal mit welchem Ansatz. 
Gruß
Marco
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 09. Apr 2009 12:02 Titel: franz Verfasst am: 09. Apr 2009 12:02 Titel: |
 |
|
Hallo Marco!
Die o.a. "halbe Ellipse" T' = 2^-(5/2) T entspricht der (von mir schlecht erinnerten) Genial-Lösung mit Sonnenradius null. Wobei mir die Vorstellung schwer fällt, daß die Erde nicht "weiterschwingt". Vielleicht wegen des fehlenden Drehimpulses?
mfG, Franz
PS Wollte ja eigentlich schweigen, doch das ist anstrengender als Hemdenbügeln. :-)
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 09. Apr 2009 12:18 Titel: as_string Verfasst am: 09. Apr 2009 12:18 Titel: |
 |
|
Hallo!
Ich denke, das hängt mit der schon erwähnten Singularität bei r=0 zusammen. Bei einem harmonischen Potential z. B. (also mit  gäbe es bei r=0 kein Problem und das "Pendel" würde einfach durch pendeln und auf der anderen Seite wieder ausschlagen. Bei einem -1/r Potential geht das Potential gegen -oo und die Kräfte würden unendlich werden. Das funktioniert natürlich kaum. Da müsste man also eigentlich dann eine Ausdehnung der Sonne annehmen, so dass das Potential bei kleinen r harmonisch wird o. ä.. Allerdings ist die Erde vorher ja so wie so schon "verglüht". gäbe es bei r=0 kein Problem und das "Pendel" würde einfach durch pendeln und auf der anderen Seite wieder ausschlagen. Bei einem -1/r Potential geht das Potential gegen -oo und die Kräfte würden unendlich werden. Das funktioniert natürlich kaum. Da müsste man also eigentlich dann eine Ausdehnung der Sonne annehmen, so dass das Potential bei kleinen r harmonisch wird o. ä.. Allerdings ist die Erde vorher ja so wie so schon "verglüht".
Wenn man einen ganz kleinen Drehimpuls annimmt, also die sehr flache Ellipse, dann funktioniert die Vorstellung vielleicht schon wieder besser. Dann kommt man auch nicht exakt zu r=0 und hat das Problem nicht.
Gruß
Marco
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Apr 2009 13:44 Titel: TomS Verfasst am: 09. Apr 2009 13:44 Titel: |
 |
|
Sorry, natürlich muss es x = sin² heißen:


 = \frac{\pi}{2})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 09. Apr 2009 23:50 Titel: franz Verfasst am: 09. Apr 2009 23:50 Titel: |
 |
|
Zwei Fragen an die "Integratoren":
Es gibt doch zwei Wurzeln bei (dr/dt)^2; warum wurde gerade diese gewählt? (Mich wundert das Integral 0 ... r0, was ja der "Rettung" der Erde entspräche. Das wollen wir doch nicht, oder? :-) ).
Ist es möglich, die Reise an der Sonnenoberfläche zu beenden? Kein großer Unterschied, ich weiß.
mfG, Franz
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Apr 2009 08:19 Titel: schnudl Verfasst am: 10. Apr 2009 08:19 Titel: |
 |
|
zum Integral:
Eigentlich ist dieses einfach lösbar, wenn man diese Substitution macht. Ich bin leider jemand der solche Ansätze nicht auf Anhieb sieht. Im Nachhinein - ja, aber...

Ich suche schon längere Zeit nach einer "Integrations-Ansatz-Sammlung" im Web, wo solche Wege nahegelegt werden. Ich hatte mal ein Schulbuch, wo es für Integrale mit bestimmtem Aussehen Lösungsansätze gab. Das waren quasi Anleitungen wie: | Zitat: | | "wenn man einen Ausdruck der Form so und so im Inegranden hat, dann mache folgende Substitution". |
Wohlgemerkt: keine Formelsammlung für fertige Integrale. Sowas hätte ich gerne wieder... Weiss jemand wo es das gibt?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
|






















