| Autor |
Nachricht |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 12. Dez 2008 12:01 Titel: Gleitreibung und Rotationsenergie Saxophon Verfasst am: 12. Dez 2008 12:01 Titel: Gleitreibung und Rotationsenergie |
 |
|
Hallo,
ich schaffe es irgendwie nicht einen konsistenten Ansatz für die folgende Aufgabe aufzuschreiben:
Gegeben ist eine Hohlkugel der Masse m und Anfangsgeschwindigkeit v*, die über eine Ebene gleitet, wobei der Reibungskoeffizient n ist. (Zu Beginn besitzt die Kugel noch keine Rotationsenergie.) Die erste Frage ist nun, mit welcher Geschwindigkeit sich die Kugel bewegt, wenn sie nur noch rollt und nicht mehr gleitet.
Die zweite Frage - nämlich die nach der von der Kugel bis zum Stillstand zurückgelegten Gesamtstrecke - verwirrt mich noch mehr, da ja kein Rollreibungskoeffizient angegeben ist.
Bei der ersten Frage würde ich einen Energieansatz machen: Die kinet. Energie zu Beginn wandelt sich in Reibungsarbeit und Rotationsenergie um. Allerdings bräuchte ich doch zur Berechnúng der Reibungsarbeit die zurückgelegte Strecke. Und außerdem kann doch die Gleitreibungskraft nicht konstant bleiben, da irgendwann gar keine Gleitbewegung mehr vorliegt. Die Gleitreibung bezieht sich ja nur auf die Strecke, die tatsächlich geglitten wird. Die Kugel rollt ja während ihrer Fortbewegung auch.
Wie gesagt bin ich sehr verwirrt und wäre euch wirklich sehr dankbar, wenn ihr mir helfen könntet, die Aufgabe zu verstehen. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. Dez 2008 16:02 Titel: Re: Gleitreibung und Rotationsenergie dermarkus Verfasst am: 12. Dez 2008 16:02 Titel: Re: Gleitreibung und Rotationsenergie |
 |
|
| Saxophon hat Folgendes geschrieben: | Allerdings bräuchte ich doch zur Berechnúng der Reibungsarbeit die zurückgelegte Strecke.
|
Nicht unbedingt. Magst du mal versuchen, alle Formeln aufzustellen, die du für diese Bewegung aufstellen kannst, und dann schauen, ob du sie so kombinieren und verwenden kannst, dass du die zurückgelegte Strecke gar nicht mehr von vorneherein zu kennen brauchst?
| Zitat: |
Und außerdem kann doch die Gleitreibungskraft nicht konstant bleiben, da irgendwann gar keine Gleitbewegung mehr vorliegt.
|
Rechne in einem ersten Schritt mal nur den Bewegungsabschnitt, in dem die Kugel mindestens noch ein bisschen gleitet. Ist dann in diesem Bewegungsabschnitt die Gleitreibungskraft konstant?
-------
Im letzten Bewegungsabschnitt könntest du dann in der Tat mit dem Rollreibungskoeffizienten den Abbremsvorgang berechnen. Wenn der nicht gegeben ist, würde ich ihn für die Rechnung einfach allgemein als  bezeichnen. bezeichnen. |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 12. Dez 2008 21:07 Titel: Saxophon Verfasst am: 12. Dez 2008 21:07 Titel: |
 |
|
Danke für die Hilfestellung!
Allerdings ist mir leider noch nicht allzu viel dazu eingefallen. Ich habe mich inzwischen auch gefragt, ob man irgendwie auch die Impulserhaltung mit ins Spiel bringen könnte, bin mir aber aufgrund der wirkenden Gleitreibungskraft unsicher. Grundsätzlich hätte ich die Gleichung
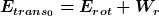 aufgestellt, wobei sich W_r wiederum in Gleitreibungsarbeit in Rollreibungsarbeit aufteilt. Der Ansatz erscheint mir also nicht sehr brauchbar. Evt. könnte ich auch einen Kraftansatz (bzw.Drehmoment) machen (fällt mir gerade ein): die Gleitreibungskraft wirkt solange, bis sich die Translations- vollständig in Rotationsenergie umgewandelt hat. Dann findet keine Winkelbeschleunigung mehr statt. Hilft mir die Beziehung aufgestellt, wobei sich W_r wiederum in Gleitreibungsarbeit in Rollreibungsarbeit aufteilt. Der Ansatz erscheint mir also nicht sehr brauchbar. Evt. könnte ich auch einen Kraftansatz (bzw.Drehmoment) machen (fällt mir gerade ein): die Gleitreibungskraft wirkt solange, bis sich die Translations- vollständig in Rotationsenergie umgewandelt hat. Dann findet keine Winkelbeschleunigung mehr statt. Hilft mir die Beziehung
 weiter? weiter? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. Dez 2008 21:56 Titel: dermarkus Verfasst am: 12. Dez 2008 21:56 Titel: |
 |
|
| Saxophon hat Folgendes geschrieben: | | Evt. könnte ich auch einen Kraftansatz (bzw.Drehmoment) machen (fällt mir gerade ein): die Gleitreibungskraft wirkt solange, bis sich die Translations- vollständig in Rotationsenergie umgewandelt hat. Dann findet keine Winkelbeschleunigung mehr statt. |
Damit bin ich fast einverstanden 
Ich würde allerdings sagen, die Gleitreibungskraft wirkt nur solange, bis die Kugel rollt und nicht mehr gleitet. Dann hat sie also durchaus noch Translationsenergie.
Kennst du schon die sogenannte Rollbedingung? |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 12. Dez 2008 23:34 Titel: Saxophon Verfasst am: 12. Dez 2008 23:34 Titel: |
 |
|
Die Rollbedingung war mir bis jetzt nicht bekannt, allerdings sehe ich gerade, dass sie im Skript steht. Besagt sie, dass die im Schwerpunkt angreifende Beschleunigung bei einer reinen Rollbewegung gleich
)) ist? ist?
Da sin(alpha)=sin 0 =0 ist auch a_s gleich Null. Ist das soweit richtig? |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 12. Dez 2008 23:53 Titel: Saxophon Verfasst am: 12. Dez 2008 23:53 Titel: |
 |
|
Oh, ich glaube, die Beziehung im letzten Beitrag war nur eine Folgerung aus der Rollbedingung  ; und letzterer Zusammenhang ist mir unmittelbar einsichtig. Wie bringt mich das nun weiter? Auflösen nach omega, und dann brauche ich noch v_s. Aber wie kann ich denn jetzt nit dem Drehmoment=0 argumentieren? ; und letzterer Zusammenhang ist mir unmittelbar einsichtig. Wie bringt mich das nun weiter? Auflösen nach omega, und dann brauche ich noch v_s. Aber wie kann ich denn jetzt nit dem Drehmoment=0 argumentieren? |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 13. Dez 2008 14:36 Titel: Saxophon Verfasst am: 13. Dez 2008 14:36 Titel: |
 |
|
Ich bin inzwischen (glaube ich) etwas weiter gekommen.
Ich weiß, dass für den Zustand, wenn nur noch Rotation stattfindet, gelten muss:
^2) . Dies habe ich einfach durch Einsetzen der Rollbedingung in die Formel für die kin.Energie erhalten. Außerdem weiß ich, dass gilt omega=t*"Winkelbeschl."; letztere ist gleich dem Drehmoment geteilt durch das Träheitsmoment. Nun ist mir aber die Zeit t unbekannt. Ist es sinnvoll zu versuchen, t zu erhalten oder sollte ich lieber nach der Strecke suchen oder nochmals nach etwas anderem? . Dies habe ich einfach durch Einsetzen der Rollbedingung in die Formel für die kin.Energie erhalten. Außerdem weiß ich, dass gilt omega=t*"Winkelbeschl."; letztere ist gleich dem Drehmoment geteilt durch das Träheitsmoment. Nun ist mir aber die Zeit t unbekannt. Ist es sinnvoll zu versuchen, t zu erhalten oder sollte ich lieber nach der Strecke suchen oder nochmals nach etwas anderem? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 13. Dez 2008 16:51 Titel: dermarkus Verfasst am: 13. Dez 2008 16:51 Titel: |
 |
|
| Saxophon hat Folgendes geschrieben: | Oh, ich glaube, die Beziehung im letzten Beitrag war nur eine Folgerung aus der Rollbedingung  ; ; |
| Saxophon hat Folgendes geschrieben: |
Ich weiß, dass für den Zustand, wenn nur noch Rotation stattfindet, gelten muss:
^2) . Dies habe ich einfach durch Einsetzen der Rollbedingung in die Formel für die kin.Energie erhalten. Außerdem weiß ich, dass gilt omega=t*"Winkelbeschl."; letztere ist gleich dem Drehmoment geteilt durch das Träheitsmoment. . Dies habe ich einfach durch Einsetzen der Rollbedingung in die Formel für die kin.Energie erhalten. Außerdem weiß ich, dass gilt omega=t*"Winkelbeschl."; letztere ist gleich dem Drehmoment geteilt durch das Träheitsmoment. |
Einverstanden 
Du scheinst als Lösungsweg irgendetwas wie "Formel nehmen, das bekannte Einsetzen, ausrechnen; das dann in eine weitere Formel einsetzen, ausrechnen, ... und fertig" zu erwarten.
Tipp: Hast du auch schon mal eine Aufgabe kennengelernt, in der du mehrere Gleichungen für mehrere Unbekannte aufstellen musstest, und aus diesem Gleichungssystem dann mit einer der mehreren möglichen Methoden, die du aus Mathe kennst, diejenige Unbekannte oder diejenigen Unbekannten bestimmt, die gesucht sind?
(Ein einfaches Beispiel dazu: Wie groß sind  und und 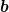 , wenn , wenn  und und  sind? Da kommst du weiter, obwohl du erstmal noch keine Gleichung hast, in die du fertig einsetzen und alles ausrechnen kannst.) sind? Da kommst du weiter, obwohl du erstmal noch keine Gleichung hast, in die du fertig einsetzen und alles ausrechnen kannst.)
Stelle erstmal alle Gleichungen auf, die du zum Rechnen brauchst und bestimme dann mit diesen Gleichungen die gesuchten Unbekannten. Das wird auch dann gehen, wenn du nach dem Aufstellen in jeder Formel zum Beispiel noch mindestens zwei Unbekannte stehen hast. |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 13. Dez 2008 18:56 Titel: Saxophon Verfasst am: 13. Dez 2008 18:56 Titel: |
 |
|
hi markus, es ist mir schon klar, dass es nicht einen einzigen Weg zur lösung gibt. manchmal gibt es aber direktere und weniger direkte wege.
das ineinandereinsetzen sollte wohl das geringere problem sein. mir fehlt noch irgendeine physikal.beziehung, die ich nicht bedenke. aber wenn du meinst, stelle ich die mir bekannten und evtl. nützlichen Gleichungen auf (ist ja auch eine gute übung):
^2
<br />
\newline E_{kin}=E_{rot}+E_{trans}+W_{r_{ges}} ) ; wobei dies offensichtlich noch nicht ausreicht. ; wobei dies offensichtlich noch nicht ausreicht. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 13. Dez 2008 19:19 Titel: dermarkus Verfasst am: 13. Dez 2008 19:19 Titel: |
 |
|
Einverstanden, diese Gleichungen wirst du brauchen können 
Achte bei der ersten noch darauf, dass die Reibungskraft ja nicht direkt gleich dem Drehmoment ist, sondern ... ? |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 13. Dez 2008 19:38 Titel: Saxophon Verfasst am: 13. Dez 2008 19:38 Titel: |
 |
|
...sondern gleich dem Drehmoment geteilt durch R.
Habe ich noch einen aufschlussreichen Zusammenhang übersehen oder fehlen mir nur ein paar triviale Formeln, sodass ich genügend gleichungen zum lösen der aufgabe bekomme? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 14. Dez 2008 01:37 Titel: dermarkus Verfasst am: 14. Dez 2008 01:37 Titel: |
 |
|
| Saxophon hat Folgendes geschrieben: | ...sondern gleich dem Drehmoment geteilt durch R.
|
Einverstanden 
Schaffst du es damit schon, loszulegen und den ersten Teil der Bewegung bis zum Beginn des Rollens zu beschreiben? |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 14. Dez 2008 12:24 Titel: Saxophon Verfasst am: 14. Dez 2008 12:24 Titel: |
 |
|
|
ich glaube nicht. Besonders die letzte der Gleichungen, der Energieansatz, bereitet mir Probleme, da doch bei W_r_ges auch die Rollreibung beachtet werden muss. Ist die Gleichung dann überhaupt hilfreich? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 14. Dez 2008 14:46 Titel: dermarkus Verfasst am: 14. Dez 2008 14:46 Titel: |
 |
|
Sag mal in Worten, wie man anfangen könnte, das ganze zu beschreiben. Welche Kraft und welches Drehmoment wirken, und was für eine beschleunigte Translationsbewegung und was für eine beschleunigte Rotationsbewegung ergeben sich damit?
Kannst du mit all den Formeln, die du nun schon hast, und mit dem, was du über solche beschleunigten Bewegungen sonst noch so weißt, anfangen, Gleichungen für diese beschleunigten Bewegungen aufzustellen? |
|
 |
Saxophon
Anmeldungsdatum: 05.12.2008
Beiträge: 35
|
 Saxophon Verfasst am: 14. Dez 2008 18:32 Titel: Saxophon Verfasst am: 14. Dez 2008 18:32 Titel: |
 |
|
Zu Beginn gleitet die Kugel mit v*. Wegen der Reibung bewirkt dies ein Drehmoment, das ich leicht berechnen kann, da der Reib.koeff. n und die Masse m der Kugel gegeben sind. Dieses Drehmoment wirkt nun die gesamte Zeit über konstant und verursacht eine Winkelbeschleunigung, die ich nun ebenfalls leicht berechnen kann. Beschleunigt wird nun solange, bis keine Gleitbewegung mehr vorliegt, bis also der Zustand eintritt, bei dem mich die Winkelgeschwindigkeit interessiert und ich weiß, dass in diesem Fall omega=winkelbeschl.*zeit gilt.
andererseits verringert sich v* permanent. Ich weiß allerdings nicht, wie ich mir die Kraft vorstellen kann, durch die v* verringert wird, wo setzt sie an? Könnte ich diese Kraft näher beschreiben, so wüsste ich nach F=ma auch die Beschleunigung (bzw. Abbremsung) a und käme dann auf v=at. t ist die gleiche Zeit wie bei der Winkelbeschleunigung und eine Beziehung zwischen v und omega liefert mir die Rollbedigung. Der Wesentliche Aspekt, der mir noch fehlt, ist also die bremsende Kraft. Was kann ich über ihre Quantität aussagen? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 15. Dez 2008 00:48 Titel: dermarkus Verfasst am: 15. Dez 2008 00:48 Titel: |
 |
|
Prima 
Für die Kraft ein Tipp: Welche Kraft ist die einzige Kraft, die von außen auf die Hohlkugel wirkt und auf die Translationsbewegung bremsend wirken kann? (Ich glaube, die Antwort ist viel einfacher als du bisher gedacht hattest  ) ) |
|
 |
|

















 )
)