| Autor |
Nachricht |
Thomasss
Anmeldungsdatum: 01.12.2010
Beiträge: 1
|
 Thomasss Verfasst am: 01. Dez 2010 18:18 Titel: Translations- und Rotationsenergie Thomasss Verfasst am: 01. Dez 2010 18:18 Titel: Translations- und Rotationsenergie |
 |
|
Meine Frage:
Hallo,
Ein homogener Vollzylinder rollt ohne zu gleiten auf einer schiefen Ebene. Wie groß ist das Verhältnis der Translations- zur Rotationsenergie um die Rotationsachse? Zeigen Sie ferner, dass die Gesamtenergie gleich der Rotationsenergie um die momentane Drehachse ist, die sich am Rand des Zylinders auf der Ebene befindet.
Meine Ideen:
irgendwie hab bekomme ich da keinen vernünftigen ansatz.
ich glaub es gilt:
kin. E = transl. E + rot. E
und transl. E = 1/2 m v^2, was mich sehr verwirrt, weil das doch die kin. E ist.
warum ist die rotationsachse auf der ebene? ich dachte eig, sie wäre im mittelpunkt des zylinders, weil seine Masse sich um den Mittelpunkt bewegt?
lg, thomas |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Dez 2010 20:06 Titel: schnudl Verfasst am: 01. Dez 2010 20:06 Titel: |
 |
|
Du kannst die Rotation ja um einen beliebigen Punkt betrachten. Die Gesamtbewegung ist immer als Überlagerung von Translation und Rotation darstellbar. Im sogenannten "Momentanpol" ist die Bewegung (wenigstens für einen kleinen Augenblick) als reine Rotation aufzufassen. Da die Unterlage sich nicht bewegt und der Zylinder nicht rutscht, ist diese Sicht kinematisch äquivalent.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
the_wire
Anmeldungsdatum: 04.11.2010
Beiträge: 81
|
 the_wire Verfasst am: 01. Dez 2010 21:06 Titel: the_wire Verfasst am: 01. Dez 2010 21:06 Titel: |
 |
|
Eine Translation ist nichts anderes (!!!) als eine geradlinige Bewegung. Das, was wir vorher immer als "kinetische Energie" betrachtet haben, war also genau genommen immer eine Translationsenergie. Nur hier unterscheiden wir die Translations- von der Rotationsenergie, weil die Rotationsenergie auch eine Form der kinetischen Energie ist!
Es gilt also:

Für den zweiten Teil der Aufgabe musst die die Rotation des Zylinders anders betrachten. Der Zylinder berührt die Ebene ja. Wenn er rollt, rollt er also AUF der Ebene. Die Auflagefläche des Zylinders (Fläche ist das falsche Wort, da es sich ja nur um eine Linie handelt) auf eben dieser Ebene kann also als Rotationsachse betrachtet werden. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 01. Dez 2010 21:29 Titel: VeryApe Verfasst am: 01. Dez 2010 21:29 Titel: |
 |
|
Ich kann auch kurvenförmig oder kreisförmig translaieren.
Translation bedeutet jeder Massepunkt hat stehts den gleichen Geschwindigkeitsvektor in Betrag und Richtung. Der Körper behält die ausrichtung im Raum auch wenn er sich auf einer Kurve bewegt. Als Ersatzbild für alle Massepunkte trägt man die Schwerpunktsgeschwindigkeit ein.
geradlinig muß das nicht unbedingt ingesamt sein. Natürlich betrachtet man das ganze über einen unendlich kleinen Zeitabschnitt dt dann geradlinig. also hast du eigentlich insofern doch recht. |
|
 |
Thom
Gast
|
 Thom Verfasst am: 02. Dez 2010 21:16 Titel: Thom Verfasst am: 02. Dez 2010 21:16 Titel: |
 |
|
mir ist das noch nicht so ganz klar geworden.
also zum ersten teil der aufgabe, zum verhältnis von Etrans und Erot:
es ist ja:
Etrans = 1/2 m v^2
Erot = 1/2 J omega^2
die lösung ist nicht:
Etrans m v^2
------- = --------------
Erot J omega^2
oder? es gilt doch auch omega = v/r |
|
 |
the_wire
Anmeldungsdatum: 04.11.2010
Beiträge: 81
|
 the_wire Verfasst am: 02. Dez 2010 21:20 Titel: the_wire Verfasst am: 02. Dez 2010 21:20 Titel: |
 |
|
Die Rotationsenergie ist nicht gleich Translationsenergie. Deine Lösung wär insofern keine Lösung, da du einfach sagst, dass beide gleich wärn 
Der Ansatz steht bereits oben. Die richtigen Formeln für die entsprechenden Energien hast du auch schon richtig. Jetzt fehlt dir nur noch das Trägheitsmoment J eines Vollzylinders, womit du das J in der Formel für Erot ersetzen kannst. |
|
 |
Thom
Gast
|
 Thom Verfasst am: 02. Dez 2010 21:43 Titel: Thom Verfasst am: 02. Dez 2010 21:43 Titel: |
 |
|
| the_wire hat Folgendes geschrieben: | Die Rotationsenergie ist nicht gleich Translationsenergie. Deine Lösung wär insofern keine Lösung, da du einfach sagst, dass beide gleich wärn 
Der Ansatz steht bereits oben. Die richtigen Formeln für die entsprechenden Energien hast du auch schon richtig. Jetzt fehlt dir nur noch das Trägheitsmoment J eines Vollzylinders, womit du das J in der Formel für Erot ersetzen kannst. |
mit Ansatz meinst du
Eges = Erot + Etrans oder?
aber ich hab Eges doch gar nicht oder? oder soll ich da die pot E = mgh hinschreiben?
J kann man glaub ich mit dem Satz von Steiner rausbekommen. laut dem ist J = m*rS^2 + Js, wobei Js der Trägheitsmoment um eine parallele Achse um den Schwerpunkt ist und rS der kürzeste Abstand zwischen Schwerpunkt und Drehachse?
aber davon habe ich doch Js und sonst auch nichts oder?
ich hab ja einige voraussetzungen. aber ich kann das einfach nicht so richtig zusammenbauen. |
|
 |
Thom
Gast
|
 Thom Verfasst am: 02. Dez 2010 22:17 Titel: Thom Verfasst am: 02. Dez 2010 22:17 Titel: |
 |
|
ich hab jetzt:
Eges = Etrans + Erot
mgh = 1/2 m v^2 + 1/2 J omega^2
mgh = 1/2 (m*v^2 + mr^2*v^2/r^2)
mgh = 1/2m (v^2+v^2)
gh=v^2
geht das so? |
|
 |
Delta
Gast
|
 Delta Verfasst am: 02. Dez 2010 22:27 Titel: Delta Verfasst am: 02. Dez 2010 22:27 Titel: |
 |
|
|
J=0.5mr^2 |
|
 |
Thom
Gast
|
 Thom Verfasst am: 02. Dez 2010 22:32 Titel: Thom Verfasst am: 02. Dez 2010 22:32 Titel: |
 |
|
| Delta hat Folgendes geschrieben: | | J=0.5mr^2 |
oh, also
mgh = 1/2 m v^2 + 1/2 J omega^2
mgh = 1/2 mv^2 + 1/2*1/2*m*r^2* v^2/r^2
gh = 1/2 (v^2 + 1/2v^2)
gh = 3/4 v^2
aber so habe ich immer noch kein verhältnis von Etrans zu Erot. ich komme nicht weiter... |
|
 |
Delta
Gast
|
 Delta Verfasst am: 02. Dez 2010 22:40 Titel: Delta Verfasst am: 02. Dez 2010 22:40 Titel: |
 |
|




Das kann man leicht zeigen
Jetzt kann man auch gut vergleichen |
|
 |
Azurech
Anmeldungsdatum: 10.11.2010
Beiträge: 64
|
 Azurech Verfasst am: 02. Dez 2010 22:41 Titel: Azurech Verfasst am: 02. Dez 2010 22:41 Titel: |
 |
|
Also ich krieg die Aufgabe auch nicht hin, dieses Thema ist nicht so meins.
ich weiß nicht, was die mit Verhältnis genau meinen und wie man sowas ausdrückt dann., gescheige denn dass ich den 2ten Teil hinkrieg.
Edit: nach deinen Formel da nun, heisst das, dass unabhängig von m und v die energie beim Vollzylinder bei der Rotation größer ist als bei der Translation? Oder wie, ich check das nicht ganz... |
|
 |
Thom
Gast
|
 Thom Verfasst am: 02. Dez 2010 22:46 Titel: Thom Verfasst am: 02. Dez 2010 22:46 Titel: |
 |
|
| Delta hat Folgendes geschrieben: | 



Das kann man leicht zeigen
Jetzt kann man auch gut vergleichen |
ah, vielen dank. jetzt hab ich verstanden. das mit dem J hatte mich verwirrt.
aber ich hab immer noch probleme mit dem zweiten teil der aufgabe. man soll ja zeigen, dass die gesamte energie gleich der Rotationsenergie ist.
aber müsste dann nicht Etrans = 0 sein?
ich denke mal, dass man da irgendwas berücksichtigen muss, wo die drehachse oder so ist und dann etwas anderes für Erot rauskommt, als wir es beim ersten Teil der Aufgabe gemacht haben? aber was ist genau anders beim zweiten Teil? |
|
 |
Delta
Gast
|
 Delta Verfasst am: 02. Dez 2010 22:54 Titel: Delta Verfasst am: 02. Dez 2010 22:54 Titel: |
 |
|
Man nimmt den Punkt wo der Zylinder aufliegt
Jetzt muß man das Trägheitsmoment aus Sicht dieses Punktes berechnen
(Steiner-Satz) |
|
 |
the_wire
Anmeldungsdatum: 04.11.2010
Beiträge: 81
|
 the_wire Verfasst am: 02. Dez 2010 23:01 Titel: the_wire Verfasst am: 02. Dez 2010 23:01 Titel: |
 |
|
Für den zweiten Teil der Aufgabe kommt dir der steiner'sche Satz zu Hilfe, mit dem du Trägheitsmomente bezüglich einer anderen Achse berechnen kannst, die parallel zur Achse durch den Schwerpunkt verlaufen.:
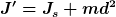
Js ist das Trägheitsmoment bezüglich einer Achse durch den Schwerpunkt, d ist der Abstand der "neuen" Rotationsachse zur Achse durch den Schwerpunkt. In diesem Fall entsprecht d dem Abstand des Schwerpunktes der Masse bis zur Auflagefläche (eigentlich eine Linie) des Vollzylinders. Das ist nichts anderes als der Radius 
Ergo:
 |
|
 |
Thom
Gast
|
 Thom Verfasst am: 02. Dez 2010 23:05 Titel: Thom Verfasst am: 02. Dez 2010 23:05 Titel: |
 |
|
| Delta hat Folgendes geschrieben: | Man nimmt den Punkt wo der Zylinder aufliegt
Jetzt muß man das Trägheitsmoment aus Sicht dieses Punktes berechnen
(Steiner-Satz) |
also ist Etrans = 1/2 J omega^2
= 1/2 (m*rS^2 + Js) * v^2/r^2
= 1/2 m*v^2/r + 1/2 Js*v^2/r^2
=1/2m*v^2(1/r + Js*m/r^2)
wenn man das so auflösen kann...
ist Js=1/2 m r^2 von eben das?
Etrans = 1/2 m v^2 (1/r+ 1/2m*v^2*m/r^2)
das stimmt irgendwie nicht...
rauskommen für Etrans soll doch wahrscheinlich Eges=3/4 m v^2, also das, was wir eben rausbekommen hatten oder? |
|
 |
the_wire
Anmeldungsdatum: 04.11.2010
Beiträge: 81
|
 the_wire Verfasst am: 02. Dez 2010 23:13 Titel: the_wire Verfasst am: 02. Dez 2010 23:13 Titel: |
 |
|
| Thom hat Folgendes geschrieben: |
rauskommen für Etrans soll doch wahrscheinlich Eges=3/4 m v^2, also das, was wir eben rausbekommen hatten oder? |
Du meinst für Eges soll herauskommen Eges = 3/4mv^2.
Wenn du den Steinersatz anwendest hast du ein neues J, nämlich das bezüglich der "momentanen" Drehachse.
Du kannst dann diese neue Energie definieren als:

Zuletzt bearbeitet von the_wire am 02. Dez 2010 23:15, insgesamt einmal bearbeitet |
|
 |
Delta
Gast
|
 Delta Verfasst am: 02. Dez 2010 23:15 Titel: Delta Verfasst am: 02. Dez 2010 23:15 Titel: |
 |
|
|
Aus Sicht des Auflagepunktes gibt es nur eine Rotation |
|
 |
|

















