| Autor |
Nachricht |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 13. Aug 2018 18:11 Titel: Gleitreibung Polynominister13 Verfasst am: 13. Aug 2018 18:11 Titel: Gleitreibung |
 |
|
Meine Frage:
Es geht um die experimentelle Bestimmung der Gleitreibungszahl. Dafür wird ein Körper m1 aus der Höhe h losgelassen und stößt am tiefsten Punkt gegen m2, der sich vorher nicht bewegt hat. m2 gleitet daraufhin um die Strecke s.
Für den Fall eines unelastischen Stoßes gilt:
 ^{2} } )
Für den Fall eines elastischen Stoßes gilt:
 ^{2} } )
Leiten Sie die Gleichungen jeweils her.
Meine Ideen:
Die erste für den unelastischen Stoß habe ich hinbekommen. Erst mit EES v1 bestimmen, dann den IES für den unelastischen Stoß (  u) ) benutzen und in dieser Gleichung dann v1 (durch die Gleichung vom EES zuvor) und u (durch Gleichsetzen von der Änderung der kinetischen Energie und der Reibungsarbeit, nach u umgestellt) eliminieren und nach ) benutzen und in dieser Gleichung dann v1 (durch die Gleichung vom EES zuvor) und u (durch Gleichsetzen von der Änderung der kinetischen Energie und der Reibungsarbeit, nach u umgestellt) eliminieren und nach 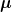 umstellen. umstellen.
Bei dem zweiten Teil der Herleitungen habe ich jetzt ein Problem, weil ich u1 einfach nicht aus dem IES eliminiert bekomme, da sich ja beide Körper nun nicht wie im ersten Fall mit gleicher Geschwindigkeit, sondern mit verschiedenen weiterbewegen. |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 14. Aug 2018 16:43 Titel: Polynominister13 Verfasst am: 14. Aug 2018 16:43 Titel: |
 |
|
Der Unterschied zwischen beiden Gleichungen ist ja nur die 4 im Zähler. Reicht vielleicht einfach eine simple Überlegung anstatt einer "komplett neuen" Herleitung  |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 14. Aug 2018 17:16 Titel: GvC Verfasst am: 14. Aug 2018 17:16 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | | Bei dem zweiten Teil der Herleitungen habe ich jetzt ein Problem, weil ich u1 einfach nicht aus dem IES eliminiert bekomme, da sich ja beide Körper nun nicht wie im ersten Fall mit gleicher Geschwindigkeit, sondern mit verschiedenen weiterbewegen. |
Hier findest Du die Herleitung der Geschwindigkeiten nach einem elastischen Stoß.
https://de.wikipedia.org/wiki/Sto%C3%9F_(Physik)#Elastischer_Sto%C3%9F
Für Deine Aufgabe ist das besonders einfach, weil die Geschwindigkeit von m2 vor dem Stoß null ist. Du musst nur für den Stoßvorgang sowohl den Impuls- als auch den Energieerhaltungsstz anwenden. |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 14. Aug 2018 17:47 Titel: Polynominister13 Verfasst am: 14. Aug 2018 17:47 Titel: |
 |
|
 komme irgendwie nicht auf eine Lösung: komme irgendwie nicht auf eine Lösung:
Mit dem EES komm ich erstmal darauf, dass die Geschwindigkeit von m1 am Punkt der Berührung  sein muss. sein muss.
Nach dem IES gilt ja vorerst pA=pE bzw.  . Wenn man jetzt noch die an m2 verrichtete Reibungsarbeit als Änderung seiner kinetischen Energie betrachtet und das nach . Wenn man jetzt noch die an m2 verrichtete Reibungsarbeit als Änderung seiner kinetischen Energie betrachtet und das nach 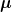 umstellt, erhält man: umstellt, erhält man:  und damit als Gesamtgleichung des Vorgangs beim elastischen Stoß vorerst: und damit als Gesamtgleichung des Vorgangs beim elastischen Stoß vorerst:
 Die einzigen schwer messbaren Größen sind ja jetzt das gesuchte Die einzigen schwer messbaren Größen sind ja jetzt das gesuchte 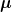 und u1. Wie genau soll ich das u1 jetzt eliminieren, hab das aus dem Wikipedia Artikel jetzt nicht erkennen können und u1. Wie genau soll ich das u1 jetzt eliminieren, hab das aus dem Wikipedia Artikel jetzt nicht erkennen können  oder doch ganz anderer Ansatz oder doch ganz anderer Ansatz |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 14. Aug 2018 17:58 Titel: GvC Verfasst am: 14. Aug 2018 17:58 Titel: |
 |
|
Du musst noch den Energieerhaltungssatz für den Stoßvorgang verwenden. Kinetische Gesamtrnergie unmittelbar vor dem Stoß ist gleich kinetische Gesamtenergie unmittelbar nach dem Stoß. Hast Du denn den Wikipedia-Artikel gar nicht durchgelesen? Da steht das doch eindeutig drin. Außerdem hatte ich Dir das ebenfalls bereits gesagt:
| GvC hat Folgendes geschrieben: | | Du musst nur für den Stoßvorgang sowohl den Impuls- als auch den Energieerhaltungsstz anwenden. |
|
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 14. Aug 2018 20:37 Titel: Polynominister13 Verfasst am: 14. Aug 2018 20:37 Titel: |
 |
|
Wenn ich den EES für den Stoß nach u1 umforme, komme ich auf:
 so richtig? so richtig? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 14. Aug 2018 21:46 Titel: GvC Verfasst am: 14. Aug 2018 21:46 Titel: |
 |
|
|
Ja, und weiter? |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 10:45 Titel: Polynominister13 Verfasst am: 15. Aug 2018 10:45 Titel: |
 |
|
Durch Einsetzen von den drei Geschwindigkeiten kommt man auf:
 ... aber wie soll man das nach (mü) umstellen ... aber wie soll man das nach (mü) umstellen  hab es schon mit Quadrieren probiert, aber dann hab ich durch die binomische Formel immer noch ne Wurzel übrig, die ich nicht mehr gescheit eliminiert bekomme hab es schon mit Quadrieren probiert, aber dann hab ich durch die binomische Formel immer noch ne Wurzel übrig, die ich nicht mehr gescheit eliminiert bekomme   |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 11:18 Titel: GvC Verfasst am: 15. Aug 2018 11:18 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | | ... aber wie soll man das nach (mü) umstellen |
So wie man das bei Gleichungen mit einer Unbekannten immer tut: So lange dieselben Rechenoperationen auf beiden Seiten der Gleichung ausführen, bis die gesuchte Größe allein auf einer Seite der Gleichung steht. Das ist Lehrstoff der Mittelstufe.
| Polynominister13 hat Folgendes geschrieben: | | hab es schon mit Quadrieren probiert, aber dann hab ich durch die binomische Formel immer noch ne Wurzel übrig, |
Dann musst Du halt nochmal quadrieren. Lass Dich von den Wurzeln doch nicht schockieren! Jedenfalls kommt bei Deiner (umständlichen) Vorgehensweise das Richtige raus. Du hast nur zu früh aufgegeben.
Du hättest auch ganz ohne Wurzeln auskommen können, wenn Du von den beiden Gleichungen
EES

und IES

die zweite Gleichung nach u1 aufgelöst und in die erste Gleichung eingesetzt hättest (Du hast es umgekehrt gemacht). Danach u2²=2µgs und v1²=2gh einsetzen und nach µ auflösen. |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 12:17 Titel: Polynominister13 Verfasst am: 15. Aug 2018 12:17 Titel: |
 |
|
Also ich komm da beim Umstellen auf dem zweiten Weg von dir, den ich ausprobiert habe, immer noch beim Auflösen der binomischen Formel auf eine Wurzel  |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 12:47 Titel: Polynominister13 Verfasst am: 15. Aug 2018 12:47 Titel: |
 |
|
Bin jetzt mehrfach auf
^{2} =4h) gekommen gekommen  |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 13:46 Titel: GvC Verfasst am: 15. Aug 2018 13:46 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | | Also ich komm da beim Umstellen auf dem zweiten Weg von dir, den ich ausprobiert habe, immer noch beim Auflösen der binomischen Formel auf eine Wurzel |
Sag mal, muss man Dir das Rechnen aus der Mittelstufe (Mathematik will ich das gar nicht nennen) wirklich vormachen? Offenbar ist es notwendig. Also dann mal Schritt für Schritt:
IES

nach u1 auflösen:

In EES
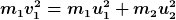
einsetzen
^2+m_2u_2^2)
m1 kürzen:
^2+\frac{m_2}{m_1}u_2^2)
Klammer ausmultiplizieren (binomische Formel):
^2+\frac{m_2}{m_1}u_2^2)
Wo ist da 'ne Wurzel, die Du beklagt hast?
Weiter: Auf beiden Seiten der Gleichung v1² subtrahieren:
^2u_2^2+\frac{m_2}{m_1}u_2^2)
Den Term mit dem Minuszeichen auf die linke Seite der Gleichung bringen (addieren):
^2u_2^2+\frac{m_2}{m_1}u_2^2)
(m2/m1)*u2 kürzen:

Ganze Gleichung quadrieren:
^2)
Aus EES für m1 vor dem Stoß ist bereits bekannt:

Aus EEs für m2 nach dem Stoß ist bekannt:

Beides einsetzen:
^2)
2g kürzen:
^2)
Nach µ auflösen:
^2)
Das ist genau die Gleichung, die hergeleitet werden sollte. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 13:48 Titel: GvC Verfasst am: 15. Aug 2018 13:48 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | Bin jetzt mehrfach auf
^{2} =4h) gekommen ?( gekommen ?( |
Aha, zwischenzeitlich bist Du ja auf das richtige Ergebnis gekommen. Hätte ich mir meinen vorigen Beitrag auch sparen können. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 13:49 Titel: GvC Verfasst am: 15. Aug 2018 13:49 Titel: |
 |
|
|
Wieso hast Du denn Deinen Bitrag mit dem richtigen Ergebnis wieder gelöscht? |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 13:58 Titel: Polynominister13 Verfasst am: 15. Aug 2018 13:58 Titel: |
 |
|
Weil ich von dem "richtigen Ergebnis" nicht auf die vorgegebene Gleichung gekommen bin  heute ist nicht mein Tag heute ist nicht mein Tag  ich hab glaube ich einfach immer viel zu früh schon die ganzen Geschwindigkeiten eingesetzt und das hat mich verunsichert ich hab glaube ich einfach immer viel zu früh schon die ganzen Geschwindigkeiten eingesetzt und das hat mich verunsichert  |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 14:10 Titel: Polynominister13 Verfasst am: 15. Aug 2018 14:10 Titel: |
 |
|
Noch eine Frage zum unelastischen Stoß:
Wenn ich die Änderung der kinetischen Energie mit der Reibungsarbeit gleichsetze, kürzt sich ja m eigentlich raus ... bei m handelt es sich ja dann nach dem unelastischen Stoß um m=m1+m2, aber vor dem Stoß hat ja nur m1 kinetische Energie und m2 keine  |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 14:19 Titel: GvC Verfasst am: 15. Aug 2018 14:19 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | Noch eine Frage zum unelastischen Stoß:
Wenn ich die Änderung der kinetischen Energie mit der Reibungsarbeit gleichsetze, kürzt sich ja m eigentlich raus ... bei m handelt es sich ja dann bei einem unelastischen Stoß um m=m1+m2, aber eigentlich hat ja bei dem Stoß nur m1 kinetische Energie und m2 keine ?( |
Ja und ...? Worauf willst Du hinaus? Beim Gleichsetzen der kinetischen Energie mit der Reibungsarbeit betrachtest Du ja den Vorgang nach dem Stoß. Und m1 hat nur Energie vor dem Stoß, nicht beim Stoß. Beim unelastischen Stoß geht ein Teil der kinetischen Energie von m1 "verloren", d.h. wird in Verformungs- und Wärmeenergie umgewandelt. |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 14:55 Titel: Polynominister13 Verfasst am: 15. Aug 2018 14:55 Titel: |
 |
|
Ergo ist meine Überlegung also doch richtig
gs= \frac{m_{1}+m_{2} }{2}u^{2} )
Die letzte Frage ist jetzt bloß, ob es sich bei dem ganzen Vorgang um einen elastischen oder unelastischen Stoß handelt. Ich würde elastisch vermuten. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 15:17 Titel: GvC Verfasst am: 15. Aug 2018 15:17 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | Ergo ist meine Überlegung also doch richtig
gs= \frac{m_{1}+m_{2} }{2}u^{2} )
Die letzte Frage ist jetzt bloß, ob es sich bei dem ganzen Vorgang um einen elastischen oder unelastischen Stoß handelt. Ich würde elastisch vermuten. |
Nein, das ist die Gleichung für den unelastischen Stoß und sie beinhaltet gleichzeitig die Tatsache, dass die kinetische Gesamtnergie vor und nach dem Stoß nicht dieselbe ist. Diese Gleichung hast Du doch für den ersten Teil der Aufgabe verwendet, bei dem es sich um einen unelastischen Stoß handelt. Ich frage mich nur, wie vor dem Hintergrund Deiner neuen Frage Deine ursprüngliche Aussage aus Deinem Eröffnungsbeitrag
| Polynominister13 hat Folgendes geschrieben: | | Die erste für den unelastischen Stoß habe ich hinbekommen. |
zu bewerten ist. Weißt Du denn nicht mehr, was Du da gemacht hast? |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 15:23 Titel: Polynominister13 Verfasst am: 15. Aug 2018 15:23 Titel: |
 |
|
Die Überlegung mit der Reibungsarbeit und Änderung der kinetischen Energie war ja nochmal auf den unelastischen bezogen 
Bleibt nur noch die Frage, ob es jetzt im Endeffekt in der Realität elastisch oder unelastisch ist  |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 15. Aug 2018 15:41 Titel: GvC Verfasst am: 15. Aug 2018 15:41 Titel: |
 |
|
| Polynominister13 hat Folgendes geschrieben: | | Bleibt nur noch die Frage, ob es jetzt im Endeffekt in der Realität elastisch oder unelastisch ist |
Das ist keine Entscheidung von Dir oder mir, sondern wird in der Aufgabenstellung vorgegeben. In der hier vorliegenden Aufgabe sollte der Gleitreibungskoeffizient für zwei unterschiedliche Fälle bestimmt (bzw. die Herleitung dafür nachvollzogen) werden, nämlich erstens für den Fall, dass es sich um einen unelastischen Stoß handelt, und zweitens für den Fall, dass es sich um einen elastischen Stoß handelt. Die beiden Fälle unterscheiden sich dadurch, dass für den eigentlichen Stoßvorgang (der hat mit den Vorgängen vor und nach dem Stoß nichts zu tun) beim unelastischen Stoß nur der Impulserhaltungssatz, nicht aber der Energieerhaltungssatz gilt, für den elastischen Stoß aber sowohl der Impuls- als auch der Energieerhaltunssatz gelten muss. Denn nur beim unelastischen Stoß geht Energie "verloren". Die "verlorene" Energie könntest Du übrigens berechnen, was aber nicht Gegenstand dieser Aufgabe war. |
|
 |
Polynominister13
Anmeldungsdatum: 14.05.2018
Beiträge: 20
|
 Polynominister13 Verfasst am: 15. Aug 2018 15:44 Titel: Polynominister13 Verfasst am: 15. Aug 2018 15:44 Titel: |
 |
|
|
Die Frage war auch nicht konkret auf die Aufgabe bezogen, sondern aus reinem Interesse gestellt. Ob es sich um einen elastischen oder unelastischen Stoß handelt, kann man wahrscheinlich am besten bei der Durchführung des Experiments selbst ermitteln. |
|
 |
|

















 oder doch ganz anderer Ansatz
oder doch ganz anderer Ansatz
 heute ist nicht mein Tag
heute ist nicht mein Tag  ich hab glaube ich einfach immer viel zu früh schon die ganzen Geschwindigkeiten eingesetzt und das hat mich verunsichert
ich hab glaube ich einfach immer viel zu früh schon die ganzen Geschwindigkeiten eingesetzt und das hat mich verunsichert 