| Autor |
Nachricht |
*andi*
Anmeldungsdatum: 08.12.2008
Beiträge: 1
|
 *andi* Verfasst am: 08. Dez 2008 22:40 Titel: Herleitung der Formel für Periodendauer eines Fadenpendels. *andi* Verfasst am: 08. Dez 2008 22:40 Titel: Herleitung der Formel für Periodendauer eines Fadenpendels. |
 |
|
Hallo liebe Physiker,
ich bin etwas unschlüssig , ob ich hier richtig bin und entschuldige mich für etwaige Unannähmlichkeiten gleichmal im Vorraus.
Zu meinem Problem:
Erst im Unterricht sollten wir die Formel der Umlaufdauer fürs Fadenpendel herleiten und zwar mit harmonischer Schwingung. Jedoch habe ich es einmal mit ein paar Formeln aus meiner Formelsammlung versucht und kam ebenfalls auf das richtige Ergebnis. Der Gag dabei ist: Die Formeln ,die ich benutzte, gelten eigentlich für Himmelskörper und deren Umlaufbahnen, bzw deren Anziehungen. (Gravitationsgesetz von Newton F=G(m1m2)/r² oder Gravitationsfeldstärke g=GM/r² beispielsweise)
Nun wollte ich fragen, ob jemand weis, warum hier das richtige Ergebnis rausgekommen ist, ob dies nur Zufall war oder ob es dafür eine logische Erklärung gibt. Mein Lehrer ( der allerdings Diplom-Physiker ist) meinte , dass er auch nicht wisse wieso das da richtig rauskommt und dass es sich ja um Himmelskörper handlen müsse, die umeinander Kreisen. Zudem brachte er noch die Bemerkung, dass ich ihn noch fertig machen würde mit meinen Herleitungen  . .
Hier meine Arbeit:
 http://img519.imageshack.us/img519/29/dsc00087fr8.th.jpg http://img519.imageshack.us/img519/29/dsc00087fr8.th.jpg
Ich bedanke mich für jegliche Hilfe
Mit freundlichen Grüßen
Andi
[Ich habe deine Rechnung hier mal als Anhang in passender Größe direkt als Anhang mit drangehängt, schönen Gruß, dermarkus]
| Beschreibung: |
|
| Dateigröße: |
71.83 KB |
| Angeschaut: |
28952 mal |

|
|
|
 |
Herbststurm

Anmeldungsdatum: 05.09.2008
Beiträge: 412
Wohnort: Freiburg i. Brsg.
|
 Herbststurm Verfasst am: 08. Dez 2008 23:09 Titel: Herbststurm Verfasst am: 08. Dez 2008 23:09 Titel: |
 |
|
Hi,
was du da gemacht hast hat nichts mit der Herleitung der Schwingungsdauer bei einem mathematischen Pendel zu tun und ist physikalisch im Kontext auch großer Humbug. Bist du sicher, dass dein Physiklehrer nicht wusste wo der Fehler liegt? Das kann ich persönlich nicht glauben....
Zu deiner Rechnung:
1.) Du hast gar keine allgemeine Planetenbewegung genommen, sondern du hast in deiner ersten Zeile klipp und klar gefordert, dass die Exzentrität Null ist, die Brennpunkte der Ellipse also zusammen fallen und man einen Kreis hat. Damit hat man eine reine Kreisbewegung.
2.) Du hast weiter verlangt, dass im Ursprung des Kreises als am Ende des Radius sich zwei Massenpunkte befinden und du hast weiter verlangt, dass die Anziehung zwischen diesen Massen gleich der Zentrifugalkraft sein soll.
Dann hast du im Kreis gerechnet, man nennt das Ringschluss und hast dann am Schluss den letzten Fehler gemacht, du hast r durch l substituiert. Auch das ist physikalisch sinnfrei, denn auch wenn der Abstand der Massenpunkte die Länge der Schnur sein soll, so hat physikalisch das eine nichts mit dem anderen zu tun.
Die Schwingungsdauer bekommt man bei dem Pendel genau so wie auch bei dem Federschwinger, jedoch ist der Weg etwas anders. Man hat eine NICHT lineare DGL.
Durch Kleinwinkelnäherung, also für kleine Auslenkungen kann man sie aber linearisieren und lösen. Sie wird dann gleich interpretiert wie beim Federschwinger und der Term

rührt daher, dass man das definiert um die Bewegungsgleichung für alle Zeiten zu erfüllen, was andernfalls nicht der Fall wäre.
Gruß
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Dez 2008 05:46 Titel: dermarkus Verfasst am: 09. Dez 2008 05:46 Titel: |
 |
|
Hallo Andi,
was du da gerechnet hast, enthält keine Fehler.  (Bis auf das vergessene Quadrat in der fünften Zeile; das war nur ein Aufschreib-Fehler zwischendrin.) (Bis auf das vergessene Quadrat in der fünften Zeile; das war nur ein Aufschreib-Fehler zwischendrin.)
Du hast hergeleitet, dass die Umlaufdauer T eines Körpers um einen Planeten mit Masse M auf einer kreisrunden Umlaufbahn

ist, wenn man den Radius dieser Umlaufbahn als 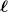 und die Zentripetalbeschleunigung auf dieser Umlaufbahn mit und die Zentripetalbeschleunigung auf dieser Umlaufbahn mit  bezeichnet, wie das für Gravitationsbeschleunigungen üblich ist. bezeichnet, wie das für Gravitationsbeschleunigungen üblich ist.
Und du hast festgestellt, dass diese Formel für die Umlaufdauer genauso aussieht wie die Formel (gültig als Näherung für kleine Auslenkwinkel) für die Schwingungsdauer eines Pendels mit Pendellänge 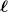 , das an einem Ort mit Gravitationsbeschleunigung g steht. , das an einem Ort mit Gravitationsbeschleunigung g steht.
Die Bewegung eines Körpers auf einer Umlaufbahn um einen Planeten herum ist also etwas sehr, sehr ähnliches wie die Schwingung eines Fadenpendels.
Konkreter:
Wenn man von der Seite auf so eine kreisförmige Umlaufbahn draufschaut, dann sieht man den Körper eine exakte harmonische Hin- und Herschwingung ausführen.
Wenn man von oben auf ein schwingendes Fadenpendel draufschaut, dann sieht man es (in guter Näherung für kleine Winkel) eine harmonische Hin- und Herschwingung ausführen.
In beiden Fällen ist die Periodendauer dieser Hin- und Herbewegung durch die Stärke der Gravitationsbeschleunigung, deren Komponente auf den schwingenden Körper wirkt, und durch den Radius der Kreisbahn, auf der der Körper sich bewegt, komplett festgelegt.
Es ist also kein Zufall, dass bei beiden Herleitungen dieselbe Formel herauskommt 
--------------------
Eine Herleitung der Schwingungsdauer für das Fadenpendel ist deine Rechnung aber natürlich nicht. Denn sie verwendet ein Modell von Himmelskörpern anstatt eines Modells für ein Fadenpendel als Ansatz. Und sie zeigt in keiner Weise, was deine Ansätze für Himmelskörper mit einem Fadenpendel zu tun haben sollen.
Um herzuleiten, welche Formel für die Periodendauer eines Fadenpendels bei kleinen Auslenkungswinkeln gilt, kommst du nicht drumherum, dir auch wirklich ein Fadenpendel genau anzuschauen und Gleichungen dafür aufzustellen. Dann kannst du entweder daraus, zum Beispiel über die Kleinwinkelnäherung und die Schwingungsdifferentialgleichung, direkt die Periodendauer des Fadenpendels herleiten. Oder aber, wenn du magst und es schaffst, das sauber zu formulieren und exakt zu vergleichen, an einer Stelle deiner Fadenpendel-Herleitung etwa sagen: "Diese Situation bzw. diese Gleichungen sind jetzt genauso wie jene Situation und jene Gleichungen bei einem Körper auf einer Umlaufbahn, also rechne ich den Rest der Herleitung wie bei dem Himmelskörper." Dafür musst du dann aber die dafür von dir zu wählende "Nahtstelle" der zwei Modelle sauber miteinander verknüpfen.
|
|
 |
|
|
















 .
.


 (Bis auf das vergessene Quadrat in der fünften Zeile; das war nur ein Aufschreib-Fehler zwischendrin.)
(Bis auf das vergessene Quadrat in der fünften Zeile; das war nur ein Aufschreib-Fehler zwischendrin.)