| Autor |
Nachricht |
kommando_pimperlepim

Anmeldungsdatum: 15.11.2004
Beiträge: 133
|
 kommando_pimperlepim Verfasst am: 02. März 2008 15:00 Titel: Stationäre Schrödinger-Gleichung für Potentialbarriere kommando_pimperlepim Verfasst am: 02. März 2008 15:00 Titel: Stationäre Schrödinger-Gleichung für Potentialbarriere |
 |
|
Wenn man die Lösung der stationären Schrödinger-Gleichung für eine endlich hohe Potentialbarriere hat, müsste man darin den Tunneleffekt erkennen können. Betrachtet werde eine von links einlaufende Welle
Betrachtet man das Betragsquadrat der Wellenfunktion (, also die Aufenthaltswahrscheinlichkeit), dann müsste sich links von der Barriere doch durch die Überlagerung mit dem reflektierten Teil eine stehende Welle bilden, d. h. das Betragsquadrat ist in diesem Bereich periodisch.
Meine Frage:
Da der austunnelnde Anteil nur eine Welle in eine Richtung ist, müsste das Betragsquadrat dort jedoch eine konstante Funktion sein? Also die Aufenthaltswahrscheinlichkeit überall gleich sein.
Ich habe dazu nur diese Bild
http://web.physik.rwth-aachen.de/~hebbeker/web-hu-lectures/hu-lectures/www-eep.physik.hu-berlin.de/_hebbeker/lectures/dem47.gif
gefunden, aber es nicht klar, was da dargestellt wurde.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 02. März 2008 15:49 Titel: as_string Verfasst am: 02. März 2008 15:49 Titel: |
 |
|
Hallo!
Ja, so ist es. Dargestellt ist offensichtlich der Realteil von psi. Das bringt Dich natürlich bei Deiner Frage, die ja eigentlich eher um den Betrag (oder Betragsquadrat, also die Aufenthaltswahrscheinlichkeit) geht, auch nicht so richtig weiter.
Wobei die Welle links auch nicht "so richtig" stehend ist, weil die Amplitude der reflektierten Welle natürlich geringer ist, als die einlaufende.
Gruß
Marco
|
|
 |
kommando_pimperlepim

Anmeldungsdatum: 15.11.2004
Beiträge: 133
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 02. März 2008 21:57 Titel: as_string Verfasst am: 02. März 2008 21:57 Titel: |
 |
|
Hallo!
Bei Bild 1 stört mich, dass die stehende Welle vor der Barriere (also links) bis 0 runter geht. Eigentlich dürfte das nicht sein, weil die reflektierte Welle ja eine kleinere Amplitude hat.
Bei Bild 2 stimmt das im Barrierenbereich tatsächlich nicht. Da muss immer eine exponentiell abklingende Funktion sein, weil die Energie des Teilchens ja geringer ist, als die des Potentials und dann bei e^(ikx) das k komplex wird, so dass die e-Funktion reell wird. Deshalb kann dieser "Überschwinger" nicht stimmen. Dann bekommst Du aber wegen den Stetigkeitsbedingungen von psi und der ersten Ableitung auch ganz andere Verhältnisse hin. Schau Dir das nochmal an.
Gruß
Marco
Edit: Ach so, bei Bild 2 soll die Energie größer als die Schwelle sein. Dann ist es natürlich wieder anders. Mmh... Müsste ich jetzt selbst noch nachrechnen.
Ich fand übrigens das mit dem Eindimensionalen Schrödinger-Zeug ganz gut im Nolting 5 beschrieben, falls Du den gerade griffbereit hast. So ein Bsp. mit Potentialschwelle sollte aber in vielen QM Büchern schon drin sein, oder?
|
|
 |
kommando_pimperlepim

Anmeldungsdatum: 15.11.2004
Beiträge: 133
|
 kommando_pimperlepim Verfasst am: 03. März 2008 07:33 Titel: kommando_pimperlepim Verfasst am: 03. März 2008 07:33 Titel: |
 |
|
Naja, ich hab hier nur den Cohen-Tannoudji zur Verfügung und der diskutiert da etwas dran vorbei ohne die Lösungen mal explizit anzugeben. Leider habe ich keine andere Literatur. Im Grunde interessiert mich nur ob ich richtig gerechnet habe, aber ich wollte nicht den kompletten Rechenweg mit Lösung hinschreiben.
Der erwähnte Punkt mit dem starken Abklingen in Bild 1 scheint nur durch die zufällig gewählten Anfangsbedingungen so. Es verschwindet nicht und ist für andere Bedingungen deutlicher über Null.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. März 2008 12:48 Titel: dermarkus Verfasst am: 03. März 2008 12:48 Titel: |
 |
|
Ich habe noch nicht ganz verstanden, wie du dir deine Welle vorstellst und einzeichnest.
Kann es sein, dass dir ein Bild wie das auf Seite 4 in
http://www.chemie.uni-bayreuth.de/pcii/de/lehre/23489/IV_stm.pdf
da entscheidend weiterhilft? Denn ich finde, diesem Bild sieht man noch deutlicher an, wo die Null der Achse für die Schwingung der Welle liegt.
Das Bild in deinem Link oben verwendet für die Welle eine nach oben verschobene Achse. Damit wird die Welle zwar übersichtlicher einzuzeichnen, aber ich glaube, du hast dich dadurch bezüglich der Frage verwirren lassen, wo der Nullpunkt der "vertikalen Wellenachse" liegen soll.
|
|
 |
kommando_pimperlepim

Anmeldungsdatum: 15.11.2004
Beiträge: 133
|
 kommando_pimperlepim Verfasst am: 05. März 2008 23:34 Titel: kommando_pimperlepim Verfasst am: 05. März 2008 23:34 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Ich habe noch nicht ganz verstanden, wie du dir deine Welle vorstellst und einzeichnest. |
| kommando_pimperlepim hat Folgendes geschrieben: |
Das Betragsquadrat der Lösung die ich dann erhalte ist in den angehängten Grafiken dargestellt. |
An sich verstehe ich die Grafiken schon, ich wollte wie gesagt nur meine Ergebnisse überprüfen und war ziemlich verwirrt, weil überall nur Darstellungen vom Realteil (statt dem physikalisch sinnvolleren Betragsquadrat) der Wellenfunktion zu finden waren.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2008 12:09 Titel: dermarkus Verfasst am: 07. März 2008 12:09 Titel: |
 |
|
Ah, okay, danke  Sorry, dass ich zunächst beim Lesen nicht genau genug hingeschaut habe Sorry, dass ich zunächst beim Lesen nicht genau genug hingeschaut habe 
Ich hab das ganze mal selbst gerechnet und beim Plotten ein bisschen mit verschiedenen Werten gespielt.
Mit deinen Annahmen  und den vier Bedingungen für die Stetigkeit der Funktion und ihrer Ableitung bin ich einverstanden, ich schlage vor, als Wert für und den vier Bedingungen für die Stetigkeit der Funktion und ihrer Ableitung bin ich einverstanden, ich schlage vor, als Wert für 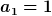 zu wählen, dann wird das Interpretieren der Diagramme etwas einfacher. zu wählen, dann wird das Interpretieren der Diagramme etwas einfacher.
Deine Diagramme kann ich bestätigen, ich denke, du hast in deiner Rechnung keinen Rechenfehler gemacht. Manches wird durch ein bisschen spielen mit den Parametern noch etwas klarer:
Für  (also für Energien (also für Energien 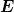 kleiner als die Potentialwallhöhe kleiner als die Potentialwallhöhe 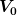 ) bekomme ich genau das Verhalten deines Diagrammes in image1.jpg. Also links ein oszillierendes Verhalten, weil die reflektierte Welle mit einem Teil der einfallenden Welle zu einer stehenden Welle interferiert, in der Mitte der exponentielle Tunnel-Abfall, und rechts der mit konstantem Betragsquadrat auslaufende Anteil (der in der Tat nicht oszilliert, da ja laut unseren Anfangsbedingungen von rechts aus dem Unendlichen nichts einlaufen soll). ) bekomme ich genau das Verhalten deines Diagrammes in image1.jpg. Also links ein oszillierendes Verhalten, weil die reflektierte Welle mit einem Teil der einfallenden Welle zu einer stehenden Welle interferiert, in der Mitte der exponentielle Tunnel-Abfall, und rechts der mit konstantem Betragsquadrat auslaufende Anteil (der in der Tat nicht oszilliert, da ja laut unseren Anfangsbedingungen von rechts aus dem Unendlichen nichts einlaufen soll).
Dass dabei die Oszillation des Betragsquadrates im Bereich links nicht ganz bis auf Null runtergeht, wie Marco schon angemerkt hat, sieht man deutlicher, wenn man die Transmission höher und damit den reflektierten Anteil kleiner wählt, zum Beispiel durch eine schmalere Barriere.
Auch mit deinem Diagramm für den Fall  bin ich einverstanden. Links sieht man wieder das von oben schon bekannte oszillatorische Verhalten (bei mir schwingt das immer durch den Wert 1, also zwischen mindestens 0 und maximal 4, weil ich bin ich einverstanden. Links sieht man wieder das von oben schon bekannte oszillatorische Verhalten (bei mir schwingt das immer durch den Wert 1, also zwischen mindestens 0 und maximal 4, weil ich 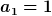 wähle), rechts wieder das Auslaufen mit konstantem Betragsquadrat (das bei mir wegen wähle), rechts wieder das Auslaufen mit konstantem Betragsquadrat (das bei mir wegen 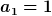 immer kleiner oder gleich 1, nämlich gleich dem transmittierten Anteil immer kleiner oder gleich 1, nämlich gleich dem transmittierten Anteil 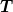 der Wellenintensität, bei mir wegen der Wellenintensität, bei mir wegen 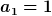 einfach einfach  , ist), und im Bereich des Potentialwalls eine mehr oder weniger starke Überhöhung, denn weil die Welle zwischen den Potentialwallkanten hin- und herreflektiert wird, nimmt das Betragsquadrat zwischen diesen Kanten Werte an, die auch mal deutlich höher sein können als überall anders in diesem Diagramm. , ist), und im Bereich des Potentialwalls eine mehr oder weniger starke Überhöhung, denn weil die Welle zwischen den Potentialwallkanten hin- und herreflektiert wird, nimmt das Betragsquadrat zwischen diesen Kanten Werte an, die auch mal deutlich höher sein können als überall anders in diesem Diagramm.
|
|
 |
|
|
















 Sorry, dass ich zunächst beim Lesen nicht genau genug hingeschaut habe
Sorry, dass ich zunächst beim Lesen nicht genau genug hingeschaut habe