| Autor |
Nachricht |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 24. Okt 2012 19:30 Titel: zweidimensionale stationäre Schrödingergleichung Maschine Verfasst am: 24. Okt 2012 19:30 Titel: zweidimensionale stationäre Schrödingergleichung |
 |
|
hallo ihr lieben,
ich hab diese woche mal wieder ne sehr schöne Aufgabe bekommen, bei der ich schon viel gerechnet habe nun aber leider nicht weiterkomme.
Ich hoffe meine berechnungen sind ers einmal soweit richtig!
Hier die Aufgabe:
Ein Teilchen befindet sich in einem zweidimensionalen Potenzial
=V_o \cdot (x^2+y^2) )
Stellen Sie die zweidimensionale Schrödingergleichung auf und zeigen Sie (durch Einsetzen), dass
 = A \cdot e^{-\frac {x^2+y^2}{a^2}})
diese Schrödingergleichung erfüllt, falls man 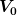 und und  passend zueinander wählt. passend zueinander wählt.
Nun meine Überlegungen:
Die stationäre Schrödingergleichung sollte sein:
}{dx^2} + \frac {d^2 \psi(x,y)}{dy^2}) + V(x,y) \cdot \psi(x,y) = E \cdot \psi(x,y) )
(Ich hoffe das ist schon mal richtig!)
Ich brauche also um Einsetzen zu können die zweiten Ableitungen von ) einmal nach einmal nach 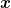 und einmal nach und einmal nach 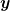
Für diese habe ich berechnet:
 }{dx^2} = 2A\cdot \frac{1}{a^2} \cdot exp [-\frac {x^2+y^2}{a^2}] \cdot (-1 + \frac {1}{a^2} \cdot 2x^2))
und
 }{dy^2} = 2A\cdot \frac{1}{a^2} \cdot exp [-\frac {x^2+y^2}{a^2}] \cdot (1 + \frac {1}{a^2} \cdot 2y^2))
Nach dem Einsetzen und ewig laaaaangem rumgerechne komme ich dann auf folgendes für die Schrödingergleichung:
 + V_0 (x^2+y^2)=E )
Nun bin ich aber mit meinem Latein am Ende.
Ich soll nun  und und 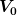 so wählen, dass die Schrödingergleichung erfüllt ist. (???) so wählen, dass die Schrödingergleichung erfüllt ist. (???)
Welcher Bedingung unterliegen  und und 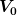 ? ?
Und wie lautet dann der Energieeigenwert E?
Ich hoffe das meine Rechnungen erst einmal soweit stimmen und das mir jemand mit den letzten drei Punkten helfen kann.
Vielen Dank! |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 24. Okt 2012 20:01 Titel: pressure Verfasst am: 24. Okt 2012 20:01 Titel: |
 |
|
|
Du hast beim einsetzten der Ableitungen in die Schrödingergleichung jeweils einen einen Term beides mal vergessen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 24. Okt 2012 20:57 Titel: Re: zweidimensionale stationäre Schrödingergleichung jh8979 Verfasst am: 24. Okt 2012 20:57 Titel: Re: zweidimensionale stationäre Schrödingergleichung |
 |
|
| Maschine hat Folgendes geschrieben: |
Für diese habe ich berechnet:
 }{dx^2} = 2A\cdot \frac{1}{a^2} \cdot exp [-\frac {x^2+y^2}{a^2}] \cdot (-1 + \frac {1}{a^2} \cdot 2x^2))
und
 }{dy^2} = 2A\cdot \frac{1}{a^2} \cdot exp [-\frac {x^2+y^2}{a^2}] \cdot (1 + \frac {1}{a^2} \cdot 2y^2))
|
Deine Funktion ist symmetrisch in x <-> y, also sollten die Ableitungen auch gleich aussehen (eines der Vorzeichen in den Klammern ist falsch).
Und wenn Du das dann eingesetzt hast:
E haengt nicht von x,y ab... was heisst das also fuer die Terme auf der linken Seite, die von x,y abhängen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Okt 2012 07:40 Titel: TomS Verfasst am: 25. Okt 2012 07:40 Titel: |
 |
|
Noch ein Tip:
nach dem Ableiten hast du symbolisch eine P(x,y)*exp(x,y), also ein Polynom in x und y sowie die e-Funktion; letztere bleibt beim Ableiten erhalten und wird zum Schluss einfach gekürzt.
Dann gilt weiter:
die x² und y² Terme aus P müssen sich gegen die aus V exakt wegheben;
die konstanten Terme in P müssen zu der Konstanten E zusammenfassen lassen
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 25. Okt 2012 13:06 Titel: Maschine Verfasst am: 25. Okt 2012 13:06 Titel: |
 |
|
|
ok wenn ich das richtig verstanden habe dann bezieht sich das - in der e Funktion nicht nur auf das x^2 sonder verhält sich wie ein Faktor -1 vor dem Quotienten? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Okt 2012 19:50 Titel: TomS Verfasst am: 25. Okt 2012 19:50 Titel: |
 |
|
ja, das Minus bezieht sich auf den Bruch
/a^2})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 29. Okt 2012 17:00 Titel: Maschine Verfasst am: 29. Okt 2012 17:00 Titel: |
 |
|
So ich habe jetzt mal noch ein wenig rumgerechnet.
Ich komme nun auf:
\cdot e^{-\frac{x^2+y^2}{a^2}})
und
\cdot e^{-\frac{x^2+y^2}{a^2}})
wenn ich das nun alles einsetze bekomme ich:
\cdot e^{-\frac{x^2+y^2}{a^2}}-2A\frac{1}{a^2}(1-2y^2\frac{1}{a^2})\cdot e^{-\frac{x^2+y^2}{a^2}}) + V_0(x^2+y^2)\cdot e^{-\frac{x^2+y^2}{a^2}} = E\cdot A\cdot e^{-\frac{x^2+y^2}{a^2}} )
jetzt teile ich durch A und die e-Funktion.
-2\frac{1}{a^2}(1-2y^2\frac{1}{a^2})) + V_0(x^2+y^2) = E)
Jetzt mach ich mir den Term noch ein wenig schöner und klammere mir -2*1/a^2 im ersten Term aus.
+(1-2y^2\frac{1}{a^2})) + V_0(x^2+y^2) = E)
jetzt löse ich die inneren Klammern auf und fasse alles zusammen.
 + V_0(x^2+y^2) = E)
nun klammere ich noch die 2 aus und auch das x^2 und y^2:
) + V_0(x^2+y^2) = E)
nun komme ich aber wieder nicht weiter! Meine x,y heben sich doch nicht gegenseitig auf so dass E niht mehr von ihnen abhängt oder sehe ich gerade vor lauter Bäumen den Wald nicht mehr? |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 29. Okt 2012 17:02 Titel: Re: zweidimensionale stationäre Schrödingergleichung Maschine Verfasst am: 29. Okt 2012 17:02 Titel: Re: zweidimensionale stationäre Schrödingergleichung |
 |
|
| jh8979 hat Folgendes geschrieben: |
Und wenn Du das dann eingesetzt hast:
E haengt nicht von x,y ab... was heisst das also fuer die Terme auf der linken Seite, die von x,y abhängen? |
Heisst das etwa das idese Terme 0 sein müssen??? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 29. Okt 2012 18:51 Titel: Re: zweidimensionale stationäre Schrödingergleichung jh8979 Verfasst am: 29. Okt 2012 18:51 Titel: Re: zweidimensionale stationäre Schrödingergleichung |
 |
|
| Maschine hat Folgendes geschrieben: |
Heisst das etwa das idese Terme 0 sein müssen??? |
Ja, diese Bedingung sagt Dir dann wie Du a waehlen musst. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 14:19 Titel: Maschine Verfasst am: 30. Okt 2012 14:19 Titel: |
 |
|
Ok ich hab jetzt noch ein wenig Zeit zumg rumrechnen gefunden.
Aber wenn ich ehrlich bin muss ich sagen, dass ich nicht wirklich genau weiss was für E am Ende rauskommen muss. Ich lege mal kurz meine Überlegungen dar.
Es gilt mit
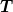 : kinetische Energie mit : kinetische Energie mit 
und
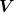 : Energie durch das angelegte Potential : Energie durch das angelegte Potential

Ich habe jetzt also :
 + V_0 \cdot (x^2+y^2) =E )
Da E unabhängig von x und y sein muss, müssen sich diese auf der linken Seite gegenseitig aufheben. Das heisst es muss gelten:
 + V_0 \cdot (x^2+y^2) = 0 )
Daraus folgt:

Jetzt bleibt noch :

nach umstellen nach a ergibt das:

Soviel zu meiner Idee...
Vlt. kann mir noch einmal jemand ein feedback geben.
LG |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Okt 2012 15:14 Titel: jh8979 Verfasst am: 30. Okt 2012 15:14 Titel: |
 |
|
| Maschine hat Folgendes geschrieben: |
Daraus folgt:

|
Diese Gleichung definiert a und nicht V_0. V_0 ist gegeben.
und somit gilt dann
 + V_0 \cdot (x^2+y^2) = \frac {2 \cdot \hbar^2}{m \cdot a^2} )
und Du kannst dann den Wert von a noch einsetzen. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 21:02 Titel: Maschine Verfasst am: 30. Okt 2012 21:02 Titel: |
 |
|
Aber laut dieser Formel wäre dann ja:

Oder meintest du den Wert für a so wie ich ihn weiter oben schon berechnet habe? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Okt 2012 21:15 Titel: jh8979 Verfasst am: 30. Okt 2012 21:15 Titel: |
 |
|
| Maschine hat Folgendes geschrieben: |
Daraus folgt:

|
Also gilt:

Und das setzt Du dann in die Formel fuer E ein. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 21:23 Titel: Maschine Verfasst am: 30. Okt 2012 21:23 Titel: |
 |
|
ah O.K.! SUPER vielen Dank!
Zur zweiten Frage welchen Bedingungen  und und 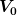 unterliegen fällt mir nur ein, das unterliegen fällt mir nur ein, das  sein muss! gibt es da noch etwas anderes zu sagen? sein muss! gibt es da noch etwas anderes zu sagen?
Und wenn nein, wie berechne ich die Energieeigenwerte? Habe gelesen das es die Summe der Erwartungswerte von V und T sind. Bin bei der letzten Vorlesung leider krank gewesen :/. Erwartungswerte kenne ich sonst nur aus der Stochastik (Wahrscheinlichkeitstheorie). |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Okt 2012 22:09 Titel: jh8979 Verfasst am: 30. Okt 2012 22:09 Titel: |
 |
|
| Maschine hat Folgendes geschrieben: | ah O.K.! SUPER vielen Dank!
Zur zweiten Frage welchen Bedingungen  und und 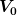 unterliegen fällt mir nur ein, das unterliegen fällt mir nur ein, das  sein muss! gibt es da noch etwas anderes zu sagen? sein muss! gibt es da noch etwas anderes zu sagen?
Und wenn nein, wie berechne ich die Energieeigenwerte? Habe gelesen das es die Summe der Erwartungswerte von V und T sind. Bin bei der letzten Vorlesung leider krank gewesen :/. Erwartungswerte kenne ich sonst nur aus der Stochastik (Wahrscheinlichkeitstheorie). |
Energieeigenwert = E = ... (siehe oben)
Wenn das alles in der letzten Vorlesung drankam, solltest Du sie *dringend* nacharbeiten. Das Verstaendnis davon (und wieso E genau der Erwartungswert ist) ist zentral fuer das Verstaendnis der QM. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 22:12 Titel: Maschine Verfasst am: 30. Okt 2012 22:12 Titel: |
 |
|
Für E habe ich jetzt folgendes raus:
 |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 22:16 Titel: Maschine Verfasst am: 30. Okt 2012 22:16 Titel: |
 |
|
|
Alles klar! Dann werde ich deinen Rat auf jeden Fall befolgen. Aber für die Aufgabe sollte es das doch dann gewesen sein!? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Okt 2012 22:17 Titel: jh8979 Verfasst am: 30. Okt 2012 22:17 Titel: |
 |
|
 |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 22:21 Titel: Maschine Verfasst am: 30. Okt 2012 22:21 Titel: |
 |
|
Danke dir  . Aber ich muss auch sagen, dass die ganze Bedeutung von diesen QM Dingen eher zu kurz in der VL kommt. Ist ne Theoretische Physik III VL und wir Mathematisieren extrem viel. Ich habe das Gefühl ich rechne mir nen Keks und weiß aber garnicht recht genau was ich denn da überhaupt berechne... . Aber ich muss auch sagen, dass die ganze Bedeutung von diesen QM Dingen eher zu kurz in der VL kommt. Ist ne Theoretische Physik III VL und wir Mathematisieren extrem viel. Ich habe das Gefühl ich rechne mir nen Keks und weiß aber garnicht recht genau was ich denn da überhaupt berechne...
Na dann muss ich mir wohl mal ein schönes Fachbuch zulegen  . .
Hast du da zufällig noch ne empfehlung parat? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Okt 2012 22:26 Titel: jh8979 Verfasst am: 30. Okt 2012 22:26 Titel: |
 |
|
| Maschine hat Folgendes geschrieben: | Danke dir  . Aber ich muss auch sagen, dass die ganze Bedeutung von diesen QM Dingen eher zu kurz in der VL kommt. Ist ne Theoretische Physik III VL und wir Mathematisieren extrem viel. Ich habe das Gefühl ich rechne mir nen Keks und weiß aber garnicht recht genau was ich denn da überhaupt berechne... . Aber ich muss auch sagen, dass die ganze Bedeutung von diesen QM Dingen eher zu kurz in der VL kommt. Ist ne Theoretische Physik III VL und wir Mathematisieren extrem viel. Ich habe das Gefühl ich rechne mir nen Keks und weiß aber garnicht recht genau was ich denn da überhaupt berechne...
Na dann muss ich mir wohl mal ein schönes Fachbuch zulegen  . .
Hast du da zufällig noch ne empfehlung parat? |
Das ist denk ich leider relativ normal. Das braucht Erfahrung und viel Uebung.
Mit Abstand das beste Buch ist meiner Meinung nach der Sakurai. Ergaenzend dazu den Schwabl, der ein wenig mehr Probleme direkt berechnet und mehr Wellenmechanik macht. |
|
 |
Maschine
Anmeldungsdatum: 18.11.2011
Beiträge: 74
|
 Maschine Verfasst am: 30. Okt 2012 22:27 Titel: Maschine Verfasst am: 30. Okt 2012 22:27 Titel: |
 |
|
Super vielen dank 
Man liest sich in diesem Semester sicherlich noch öfter 
Bis dann
Und DANKE |
|
 |
|

















 . Aber ich muss auch sagen, dass die ganze Bedeutung von diesen QM Dingen eher zu kurz in der VL kommt. Ist ne Theoretische Physik III VL und wir Mathematisieren extrem viel. Ich habe das Gefühl ich rechne mir nen Keks und weiß aber garnicht recht genau was ich denn da überhaupt berechne...
. Aber ich muss auch sagen, dass die ganze Bedeutung von diesen QM Dingen eher zu kurz in der VL kommt. Ist ne Theoretische Physik III VL und wir Mathematisieren extrem viel. Ich habe das Gefühl ich rechne mir nen Keks und weiß aber garnicht recht genau was ich denn da überhaupt berechne...
 .
.