| Autor |
Nachricht |
Ronny1
Gast
|
 Ronny1 Verfasst am: 02. Mai 2014 10:08 Titel: Zweidimensionale dynamische Systeme Ronny1 Verfasst am: 02. Mai 2014 10:08 Titel: Zweidimensionale dynamische Systeme |
 |
|
Meine Frage:
Hallo liebes Physikerboard,
betrachten wir ein dynamisches System, dass durch ein System linearer Differentialgleichungen erster Ordnung mit reellen, konstanten Koeffizienten 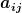 beschrieben wird. beschrieben wird.

Wir bezeichnen mit 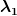 und und  die Eigenwerte der Matrix A. die Eigenwerte der Matrix A.
a) Unter welchen Bedingungen sind die Eigenwerte 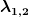 reell? Untersuchen Sie folgende drei Fälle: reell? Untersuchen Sie folgende drei Fälle:
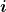 \lambda_1 < \lambda_2 < 0)
 \lambda_1 < 0 < \lambda_2)
 0 < \lambda_1 < \lambda_2.)
Stellen Sie die Bedingungen an A auf um diese drei Fälle zu unterscheiden. Skizziere Sie das Phasenportrait des Systems in der -\text{Ebene}) für jeden der Fälle. für jeden der Fälle.
b) Unter welchen Bedingungen sind die Eigenwerte 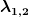 komplex? Unterscheiden Sie die Fälle: komplex? Unterscheiden Sie die Fälle:
 Re(\lambda_{1,2}) > 0) und und
 Re(\lambda_{1,2}) < 0) . .
Skizzieren Sie eine typische Trajektorie des Systems in der -\text{Ebene}) für die beiden Fälle. für die beiden Fälle.
Tipp: Es kann hilfreich sein, den gedämpften harmonischen Oszillator aus als dynamisches System zu betrachten.
Meine Ideen:
Also ich stehe auf dem Schlauch. Die Eigenwerte bestimmt man ja indem man das charakteristische Polynom löst, aber wie mache ich das hier? Muss ich das machen?
Ich weiß nicht wie ich das handhaben soll und wie ich die Bedingungen prüfen soll und diese aufstellen soll an A um diese zu unterscheiden?
Danke LG Ronja |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 02. Mai 2014 11:22 Titel: Re: Zweidimensionale dynamische Systeme jh8979 Verfasst am: 02. Mai 2014 11:22 Titel: Re: Zweidimensionale dynamische Systeme |
 |
|
| Ronny1 hat Folgendes geschrieben: |
Also ich stehe auf dem Schlauch. Die Eigenwerte bestimmt man ja indem man das charakteristische Polynom löst, aber wie mache ich das hier? Muss ich das machen?
|
Ja, musst Du und wenn Du die Eigenwerte hast, kannst Du gucken wan Sie reel und komplex sind... |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 02. Mai 2014 17:28 Titel: Re: Zweidimensionale dynamische Systeme Ronny1 Verfasst am: 02. Mai 2014 17:28 Titel: Re: Zweidimensionale dynamische Systeme |
 |
|
Gut. Ich bedanke mich ganz herzlich.
Nun ich denke es sind die Eigenwerte von

gefragt?
Charak. Polynom
 \cdot (a_{2 2} y_2 - \lambda) - (a_{2 1} y_1) \cdot (a_{1 2} y_2) =
<br />
\lambda^2 - a_{1 1} y_1 \lambda - a_{2 2} y_2 \lambda + a_{1 1} y_1 a_{2 2} y_2 - (a_{2 1} y_1) \cdot (a_{1 2} y_2))
Nun PQ-Formel aber was geschieht mit dem restlichen Termen am Ende?
Das ist dann quasi von  mein q? mein q?
Also:
^2 + (a_{2 1} y_1) \cdot (a_{1 2} y_2)})
Das könnte ich jetzt noch ausrechnen, aber großartige Vereinfachung sehe ich dann jetzt auch nicht.
| Zitat: | | kannst Du gucken wan Sie reel und komplex sind... |
Ich gucke, aber aus dem wirr kann ich nicht wirklich herausfinden, wann die Eigenwerte reell und wann sie komplex sein könnten.
LG Ronja
PS: Stimmt das bis jetzt? |
|
 |
Jannick
Anmeldungsdatum: 25.07.2012
Beiträge: 107
|
 Jannick Verfasst am: 02. Mai 2014 19:06 Titel: Jannick Verfasst am: 02. Mai 2014 19:06 Titel: |
 |
|
Deine erste Gleichung ist falsch, das das Produkt aus einer quadr. Matrix und einem Vektor ein Vektor ist. Die Matrix die zu diagonalisieren ist, ist einfach die Matrix, die nur aus a_11 a_12 usw. besteht. Deine Lösung ist allerdings trotzdem ok, wenn du einfach alle y's vergisst bzw. 1 setzt. Die Eigenwerte sind dann reell, wenn der Term unter der Wurzel positiv ist.
Z.b. ist dies der Fall, wenn a_12 und a_21 das selbe Vorzeichen haben. |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 08:35 Titel: Re: Zweidimensionale dynamische Systeme Ronny1 Verfasst am: 03. Mai 2014 08:35 Titel: Re: Zweidimensionale dynamische Systeme |
 |
|
Okay, vielen Dank. Danke korrigiere ich mich mal:

Davon das charakteristische Polynom lautet:

 \cdot (a_{2 2} - \lambda) - (a_{2 1}) \cdot (a_{1 2}) =
<br />
\lambda^2 - a_{1 1} \lambda - a_{2 2}\lambda + a_{1 1} a_{2 2} - a_{2 1} a_{1 2})
Nun PQ-Formel:
^2 + a_{2 1} a_{1 2}})
So stimmt das jetzt.
| Zitat: | Die Eigenwerte sind dann reell, wenn der Term unter der Wurzel positiv ist.
Z.b. ist dies der Fall, wenn a_12 und a_21 das selbe Vorzeichen haben. |
Das sehe ich auch. Aber es ist ja noch ein Stück weit genauer gefragt.
 \lambda_1 < \lambda_2 < 0)
 \lambda_1 < 0 < \lambda_2)
 0 < \lambda_1 < \lambda_2)
Also ich bekomme jetzt explizit heraus:
^2}{4}+ a_{2 1} a_{1 2}})
^2}{4}+ a_{2 1} a_{1 2}})
Ich meine, aber wie soll da noch unterscheiden, irgendwie wenn ich die einzelnen Komponente "wähle". Der erste Fall kann doch schon gar nicht eintreten, weil 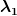 immer größer immer größer  ist? Obwohl das kann man auch nicht sagen, wenn man nichts konkretes einsetzt, von daher schwirre ich hier in Gedanken und reiße mir die Haare vom Kopf und komme einfach nicht weiter ist? Obwohl das kann man auch nicht sagen, wenn man nichts konkretes einsetzt, von daher schwirre ich hier in Gedanken und reiße mir die Haare vom Kopf und komme einfach nicht weiter 
Please 
Danke & LG
Ronja |
|
 |
T.rak92
Anmeldungsdatum: 25.01.2012
Beiträge: 296
|
 T.rak92 Verfasst am: 03. Mai 2014 11:25 Titel: T.rak92 Verfasst am: 03. Mai 2014 11:25 Titel: |
 |
|
Unter der wurzel hast du glaube ich einen Term vergessen.
Ansonsten die Eigenwerte einfach umbenennen, sonst klappt es nicht. |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:12 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:12 Titel: |
 |
|
 Was fehlt denn unter der Wurzel noch? Sehe den Fehler nicht. Wie soll ich die Eigenwerte umbenennen? Was fehlt denn unter der Wurzel noch? Sehe den Fehler nicht. Wie soll ich die Eigenwerte umbenennen?
LG Ronja |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:31 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:31 Titel: |
 |
|
Sehr interessant, hilft mir jedoch nicht, sry:/
LG Ronja |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 03. Mai 2014 22:32 Titel: jh8979 Verfasst am: 03. Mai 2014 22:32 Titel: |
 |
|
|
-->> Mitdenken.... |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:33 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:33 Titel: |
 |
|
Hab ich  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 03. Mai 2014 22:34 Titel: jh8979 Verfasst am: 03. Mai 2014 22:34 Titel: |
 |
|
|
Bezweifel ich stark... |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:36 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:36 Titel: |
 |
|
Skeptizismus ist der Anfang des Glaubens.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 03. Mai 2014 22:37 Titel: jh8979 Verfasst am: 03. Mai 2014 22:37 Titel: |
 |
|
|
Ok. Ist anscheinend sinnlos... viel Spaß mit der Aufgabe... |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:39 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:39 Titel: |
 |
|
|
Sinnlos? Ich habe die PQ-Formel wohl angewendet, oder nicht? Was zum Teufel soll mir der Link zur PQ-Formel bitte bringen? Bei aller Achtung, sry? Entweder man will jemanden helfen, oder jemanden auf die Nerven gehen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 03. Mai 2014 22:40 Titel: jh8979 Verfasst am: 03. Mai 2014 22:40 Titel: |
 |
|
|
Offensichtlich hast Du es falsch gemacht... und bist anscheinend zu uneinsichtig das zu merken... |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:46 Titel: Re: Zweidimensionale dynamische Systeme Ronny1 Verfasst am: 03. Mai 2014 22:46 Titel: Re: Zweidimensionale dynamische Systeme |
 |
|
Und dann fehlt halt der Term

unter der Wurzel. Ist es jetzt das Hauptproblem? Kann man es nicht direkt sagen? Lieber an den Fehler des Mitmenschen zusehen und ihn quälen lassen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 03. Mai 2014 22:47 Titel: jh8979 Verfasst am: 03. Mai 2014 22:47 Titel: |
 |
|
|
Dann fehlt er halt.... ist mir ziemlich egal .. genauso wie dir anscheinend... |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:53 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:53 Titel: |
 |
|
Zuerst war es Uneinsichtigkeit, jetzt ist's Gleichgültigkeit.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
 jh8979 Verfasst am: 03. Mai 2014 22:54 Titel: jh8979 Verfasst am: 03. Mai 2014 22:54 Titel: |
 |
|
|
Das war es von Anfang an .. |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 22:56 Titel: Ronny1 Verfasst am: 03. Mai 2014 22:56 Titel: |
 |
|
|
Hast noch weitere pädagogisch wertvolle Links parat oder magst weiter polemisieren? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. Mai 2014 22:59 Titel: as_string Verfasst am: 03. Mai 2014 22:59 Titel: |
 |
|
@Ronny:
Dir ist es vielleicht nicht bewusst, aber Dir wollen Leute helfen. Also bitte... Reiß Dich zusammen!
Gruß
Marco |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 23:05 Titel: Ronny1 Verfasst am: 03. Mai 2014 23:05 Titel: |
 |
|
Entschuldigung Marco, aber ich glaube, dass es einfacherer und schneller wäre auf Fehler direkt aufmerksam zu machen, wie es T.rak92 gemacht hat?
Entschuldigung jh8979 habe heute einen schlechten Tag..  |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. Mai 2014 23:06 Titel: as_string Verfasst am: 03. Mai 2014 23:06 Titel: |
 |
|
Also... Ich hab den Thread jetzt mal kurz überflogen. @Ronny1: Ist es denn so schwer, nochmal alle Terme zu überprüfen?
Welche Summanden haben ein lambda drin und welche haben keines in der ursprünglichen Gleichung? Die, die keines haben (das ist nicht nur einer!) werden zum q zusammen gefasst, die mit einem lambda zum p.
Das musst Du schon selbst hinbekommen...
Gruß
Marco |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. Mai 2014 23:08 Titel: as_string Verfasst am: 03. Mai 2014 23:08 Titel: |
 |
|
Naja, wir versuchen eben gerade nicht so direkt hinzuweisen. Am meisten lernt man eben, wenn man möglichst viel selbst heraus findet.
Ich weiß, dass das oft falsch als "Lustigmachen" oder "nerven" empfunden wird und sich solche Fragen dann ewig hinziehen. Aber die pq-Formel richtig anzuwenden, das schaffst Du schon noch selbst. Den Hinweis, dass da was nicht stimmt, hast Du ja recht schnell bekommen.
Gruß
Marco |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 03. Mai 2014 23:20 Titel: Re: Zweidimensionale dynamische Systeme Ronny1 Verfasst am: 03. Mai 2014 23:20 Titel: Re: Zweidimensionale dynamische Systeme |
 |
|
Ja absolut Marco. Aber jetzt weiterschauend machen mich die zu analysierenden Bedingungen fertig.
 \lambda_1 < \lambda_2 < 0)
 \lambda_1 < 0 < \lambda_2)
 0 < \lambda_1 < \lambda_2)
Die Lösungen sind ja:
^2}{4}+ a_{2 1} a_{1 2}- a_{1 1} a_{2 2}})
^2}{4}+ a_{2 1} a_{1 2}- a_{1 1} a_{1 2}})
| as_string hat Folgendes geschrieben: | Naja, wir versuchen eben gerade nicht so direkt hinzuweisen. Am meisten lernt man eben, wenn man möglichst viel selbst heraus findet.
Ich weiß, dass das oft falsch als "Lustigmachen" |
Ja schon, aber ich glaube nicht, dass es immer die gute Variante ist. Denn jeder macht mal Fehler und jeder weiß wohl selbst genau, wie nervig es ist manchmal selbst stundenlang danach zu suchen.
Danke und sry nochmal
Ronja |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. Mai 2014 23:23 Titel: as_string Verfasst am: 03. Mai 2014 23:23 Titel: |
 |
|
Aah, ich sehe die Terme!!! 
Noch mit dem "Umbennen" vielleicht: Du hast ja bei Deinen 3 Fällen immer, dass lambda 1 kleiner ist als lambda 2. Wenn Du Dir jetzt mal anschaust, was Du für lambda 1 und 2 raus hast, meinst Du dass es jemals möglich sein wird, dass eine der drei Bedingungen erfüllt wird?
Schau mal ob es besser klappt, wenn Du einfach lambda 1 -> lambda 2 nennst und umgekehrt.
Gruß
Marco |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 04. Mai 2014 07:36 Titel: Ronny1 Verfasst am: 04. Mai 2014 07:36 Titel: |
 |
|
| as_string hat Folgendes geschrieben: |
Noch mit dem "Umbennen" vielleicht: Du hast ja bei Deinen 3 Fällen immer, dass lambda 1 kleiner ist als lambda 2.
|
Genau das ist der Fall.
| as_string hat Folgendes geschrieben: |
Wenn Du Dir jetzt mal anschaust, was Du für lambda 1 und 2 raus hast, meinst Du dass es jemals möglich sein wird, dass eine der drei Bedingungen erfüllt wird?
|
Ja das ist in der Tat ziemlich unmöglich.
| as_string hat Folgendes geschrieben: |
Schau mal ob es besser klappt, wenn Du einfach lambda 1 -> lambda 2 nennst und umgekehrt.
|
Wenn ich jetzt die Variablen einfach vertausche, dann ist jedenfalls immer  erfüllt. erfüllt.
Aber jetzt müsste ich irgendwie die Komponenten wählen, dass in Bedingung (i) beide Lösungen < 0 sind und immer noch gilt, dass  . .
Bei (ii) muss ich hinbekommen, dass  und und 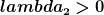 ist. ist.
Bei (iii) halt, dass beide Lösungen > 0 sind und wie auch schon bei (i) gilt, dass  ist. ist.
Jetzt frage ich mich, ob ich mit einem System darangehen kann oder einfach mich durch's probieren daranhänge? Bis dann,
danke und sry nochmal
Ronja |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 04. Mai 2014 11:58 Titel: as_string Verfasst am: 04. Mai 2014 11:58 Titel: |
 |
|
Hallo!
Mmh... Leider bin ich nicht so der Mathematiker und das alles ist bei mir schon ziemlich lange her... Mit anderen Worten... Ich weiß das alles leider nicht mehr wirklich so genau... 
Was ich aber noch sagen kann: So eine Matrix kann positiv oder negativ definit sein (wenn beide Eigenwerte positiv oder beide negativ sind) oder auch indefinit. (Semidefinit lässt jeweils auch zu, dass einer der Werte genau 0 ist.)
Schau Dir vielleicht dazu auch kurz die Wikiseite zur Definitheit an.
Die Fälle, die Du betrachten sollst, sind also gerade die unterschiedlich definiten. Das spielt auch bei partiellen Diff-Gleichungen eine große Rolle: Wenn positiv oder negativ definit, dann ist es eine elliptische, wenn indefiniti eine hyperbolische und semidefinit (wieder positiv oder negativ) eine parabolische, wenn ich mich recht erinnere.
Was das im Einzelnen genau bedeutet etc. das müsste ich auch erst wieder lesen... Bei Wikipedia gibt es zu so mathematischen Themen echt extrem gute Seiten, finde ich. Vielleicht schaust Du Dich dort erst noch um?
Gruß
Marco |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 04. Mai 2014 12:02 Titel: as_string Verfasst am: 04. Mai 2014 12:02 Titel: |
 |
|
Ach so, und rein rechnerisch: Du kannst natürlich sagen; wenn der Wurzel-Wert größer als der Betrag von dem vor dem plus/minus ist, dann ist das eine Lambda positiv (das mit dem Plus) und das andere negativ. Ansonsten sind entweder beide negativ oder beide positiv, je nachdem, ob der Wert vor dem plus/minus positiv oder negativ ist.
Jetzt mal salopp ausgedrückt...
Gruß
Marco |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 04. Mai 2014 12:06 Titel: Ronny1 Verfasst am: 04. Mai 2014 12:06 Titel: |
 |
|
Okay, nun gut. Ich hatte es bis heute noch gar nicht. Dann lese ich mich mal ein und melde mich dann. Jedoch wenn du es nicht erwähnt hättest, dann wüsste ich gar nicht, dass sowas existiert bzw. dass es dies zum Lösen der Aufgabe führt.
LG Ronja |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 05. Mai 2014 13:36 Titel: Ronny1 Verfasst am: 05. Mai 2014 13:36 Titel: |
 |
|
| as_string hat Folgendes geschrieben: |
Was ich aber noch sagen kann: So eine Matrix kann positiv oder negativ definit sein (wenn beide Eigenwerte positiv oder beide negativ sind) oder auch indefinit. (Semidefinit lässt jeweils auch zu, dass einer der Werte genau 0 ist.)
|
Ich habe mich jetzt damit auseinandergesetzt jedoch wird mir daraus nicht klar, wie ich die nötigen Informationen auf meine Probleme überbringe.
Zu den Eigenwerten hast du ja schon was gesagt. Allgemein gilt aber:
eine quadratische symmetrische (bzw. hermitesche) Matrix ist genau dann
positiv definit, wenn alle Eigenwerte größer als Null sind;
positiv semidefinit, wenn alle Eigenwerte größer oder gleich Null sind;
negativ definit, wenn alle Eigenwerte kleiner als Null sind;
negativ semidefinit, wenn alle Eigenwerte kleiner oder gleich Null sind:
indefinit, wenn positive und negative Eigenwerte existieren.
Wie Marco schon sagte interessieren mich ja die Fälle, also die unterschiedlich definiten. Sprich die indefiniten. Ich verstehe nur nicht was ich davon für die Aufgabe mitnehmen soll?
LG Ronja |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 05. Mai 2014 14:41 Titel: as_string Verfasst am: 05. Mai 2014 14:41 Titel: |
 |
|
In der Aufgabe sind doch aber drei Fälle unterschieden, und zwar genau die, wo beide kleiner 0, einer kleiner und einer größer 0 und als drittes beide größer 0 sind. Das sind doch genau die drei Fälle: negativ definit, indefinit und positiv definit.
Hatte ich das nicht auch schon so in etwa geschrieben gehabt.
Ich hatte doch auch schon geschrieben, welche Bedingungen an die beiden Summanden gestellt werden müssen, um jeweils einen der drei Fälle zu erhalten.
Mehr ist doch eigentlich in der Aufgabe auch gar nicht gefragt, oder?
Gruß
Marco |
|
 |
Ronny1
Gast
|
 Ronny1 Verfasst am: 05. Mai 2014 16:30 Titel: Ronny1 Verfasst am: 05. Mai 2014 16:30 Titel: |
 |
|
| as_string hat Folgendes geschrieben: |
Mehr ist doch eigentlich in der Aufgabe auch gar nicht gefragt, oder?
|
Ja stimmt, sry habe es überlesen. Bei der Skizze des Phasenportraits in der (y1,y2)-Ebene weiß ich nicht wie ich für jeden der Fälle. Was soll ich gegen was auftragen? Phasenportrait ist ja ein äquivalenter Begriff zu Phasenraum. Trotzdem kriege ich das nicht hin.
Beim Aufgabenteil b) soll ich die Bedingungen finden bei denen die Eigenwerte komplex sind. Das Schemata ist ja gleich, oder irre mich da? Worauf ich hinaus will ist, dass die Berechnung ja übertragbar ist bis zum Zeitpunkt des Einsetzens der PQ-Formel? Da tritt ja dann die "Komplexität" auf, wenn unter der Wurzel was negatives herauskommen würde. Aber dieser Fall würde nur eintreten wenn die ersten zwei Summanden kleiner dem letzten Subtrahenden wären. Aber im Prinzip ist das ja wieder egal was ja nur um den Realteil gefragt ist sprich (a11+a22)/2. Gelten da die gleichen "Regeln" wie für die reellen Matrizen?
Danke. LG Ronja |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 06. Mai 2014 10:20 Titel: as_string Verfasst am: 06. Mai 2014 10:20 Titel: |
 |
|
Wie gesagt, ich weiß das alles nicht mehr so genau. Deshalb verlasse Dich bitte nicht zu sehr auf das, was ich hier schreibe. Immer nochmal nachschauen, ob Du im Internet etwas dazu findest, was das untermauern oder vielleicht widerlegen könnte...
| Ronny1 hat Folgendes geschrieben: | | as_string hat Folgendes geschrieben: |
Mehr ist doch eigentlich in der Aufgabe auch gar nicht gefragt, oder?
|
Ja stimmt, sry habe es überlesen. Bei der Skizze des Phasenportraits in der (y1,y2)-Ebene weiß ich nicht wie ich für jeden der Fälle. Was soll ich gegen was auftragen? |
Die eine Achse ist y1, die andere y2. Die Matrix bildet ja letztlich einen Punkt in dieser Ebene auf eine Veränderung dieser Koordinaten ab, quasi eine Art "Geschwindigkeit" in diesem Phasenraum. Wenn sie nur positive Eigenwerte hat, also positiv definit ist, werden positive y1 Werte auf positive "y1-Veränderungen" abgebildet und für y2 genau so. Negative werden aber auch auf negative abgebildet. Das Phasenraumvolumen würde demnach ständig anwachsen.
Bei negativ definit würde es ständig kleiner werden.
Schau Dir dazu mal den harmonischen Oszillator mit Dämpfung an (z. B. aktuell auch in diesem Thread hier: http://www.physikerboard.de/topic,38305,-gedaempfter-harmonischer-oszillator.html). Rechne da mal die Eigenwerte aus. Da wirst Du sehen, dass sie für den Schwingfall komplex sind, für den Kriechfall reell und die Matrix negativ definit ist.
Übrigens: Gebe doch erstmal ein Bedingungen an die Koeffizienten an, bei denen die Eigenwerte reell und die Matrix entsprechend definit wird! Ich denke, das ist in der Aufgabe auch gefordert.
| Ronny1 hat Folgendes geschrieben: | | Beim Aufgabenteil b) soll ich die Bedingungen finden bei denen die Eigenwerte komplex sind. Das Schemata ist ja gleich, oder irre mich da? Worauf ich hinaus will ist, dass die Berechnung ja übertragbar ist bis zum Zeitpunkt des Einsetzens der PQ-Formel? Da tritt ja dann die "Komplexität" auf, wenn unter der Wurzel was negatives herauskommen würde. |
Ja, genau den Fall musst Du aber finden. Für welche Werte von axx wird das unter der Wurzel denn negativ? Für welche positiv? Das ist genau das, was in der Aufgabe ja erstmal gefragt ist!
| Ronny1 hat Folgendes geschrieben: | | Aber dieser Fall würde nur eintreten wenn die ersten zwei Summanden kleiner dem letzten Subtrahenden wären. Aber im Prinzip ist das ja wieder egal was ja nur um den Realteil gefragt ist sprich (a11+a22)/2. Gelten da die gleichen "Regeln" wie für die reellen Matrizen? |
Dir ist schon klar, dass die axx auch teilweise negativ sein können? Nur der erste Summand mit dem Quadrat ist sicher positiv!
Minimal kannst Du den Ausdruck unter der Wurzel auch vereinfachen, wenn Du die Klammer mit dem Quadrat mal ausmultiplizierst.
Also, mache ersteinmal das hier: Nimm den Ausdruck unter der Wuzel. Verwende die 1. Binomisch Formel und fasse danach wieder mit der 2. Binomischen Formel zusammen, so dass Du nur noch zwei Summanden da stehen hast, von denen einer wieder ein Quadrat hat.
Dann machst Du eine Ungleichung und setzt den Wurzel-Term größer - bzw. für komplexe Lösungen kleiner - 0. Dann hast Du schon mal die gesuchte Bedingung.
Gruß
Marco |
|
 |
|


















 Was fehlt denn unter der Wurzel noch? Sehe den Fehler nicht. Wie soll ich die Eigenwerte umbenennen?
Was fehlt denn unter der Wurzel noch? Sehe den Fehler nicht. Wie soll ich die Eigenwerte umbenennen?





