| Autor |
Nachricht |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 31. Jul 2007 17:25 Titel: statische Maxwellglen+Kovarianz=dynamische Maxwellglen! michifold Verfasst am: 31. Jul 2007 17:25 Titel: statische Maxwellglen+Kovarianz=dynamische Maxwellglen! |
 |
|
Hallo,
in den einführenden Kapiteln in Misner/Thorne/Wheeler´s "Gravitation" steht etwas sehr Interessantes zu den Maxwellgleichungen, nämlich dass man mit Hilfe der statischen Maxwellgleichungen und der Annahme der Kovarianz der Naturgesetze zu den dynamischen Maxwellgleichungen kommt!
Das heißt, dass man nur 2 der 4 Maxwellgleichungen braucht! und sogar bloß die 2 Einfachen!
Vorgerechnet wird das im Buch für die Divergenzfreiheit des B-Feldes:
 gilt in allen IS: Labor, und Rakete: gilt in allen IS: Labor, und Rakete:
Labor: 
Rakete: 
Nehmen wir, an die Rakete bewegt sich in x-Richtung. Dann gilt für die Differentialoperatoren und für das Magnetfeld (c=1):


also:
+\beta \gamma(\partial_t B_x + \partial_y E_z - \partial_z E_y) )
Damit bekommen wir also tatsächlich

und (da für Boosts in in y und z-Richtung analog)

Da haben MTW recht wenn sie sagen: "How beautiful..."
Ich, völlig hin und weg auf Grund dieses neuen tiefen Einblicks in die Schönheit der Natur ( ), frage mich, ob das wohl auch für die elektrostatische Maxwellgleichung ), frage mich, ob das wohl auch für die elektrostatische Maxwellgleichung
 hinhaut? (Rechnung steht nicht im Buch und würde auch wegen den verwendeten "infinitesimalen" Lorentztrafos, wo gamma=1 gesetzt wird nicht gehen) hinhaut? (Rechnung steht nicht im Buch und würde auch wegen den verwendeten "infinitesimalen" Lorentztrafos, wo gamma=1 gesetzt wird nicht gehen)
Labor: 
Rakete:  (lorentzkontrahierte Ladungsdichte) (lorentzkontrahierte Ladungsdichte)
Wenn man das Einsetzspielchen wiederholt steht da:
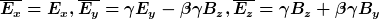
folgt:
+\beta \gamma(\partial_t E_x - (\partial_y B_z - \partial_z B_y)) )
da ja 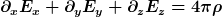 folgt jetzt , dass folgt jetzt , dass
=4\pi \rho \frac{\gamma^{-1}-\gamma}{\beta \gamma}=-4 \pi \beta \rho=- 4 \pi j_x)
Damit lautet die dynamische Maxwellgleichung 
Somit haben wir aus den mathematischen Formulierungen dafür, dass es keine magnetischen Monopole gibt, dass die Quellen und Senken des elektrischen Feldes elektrische Ladungen sind und, dass die Naturgesetze unabhängig von der speziellen Wahl des Inertialsystems gelten, also kovariant sind, die dynamischen Maxwellgleichungen herleiten können!
Es ist wirklich unfaßbar, dass dieses (für mich) atemberaubende Resultat in keinem Buch über Elektrodynamik (weder in Nolting, Fließbach, Jackson hab ich was gefunden) und auch nicht in der Vorlesung oder sonstwo im Internet (zumindest bis jetzt  ) zu finden ist? ) zu finden ist?
Ich kann wirklich nur jedem empfehlen, der sein Wissen über Elektrodynamik, SRT und ART von (oft) langweiligem Gerechne auf tiefgehendes Verständnis erweitern will sich das Buch der 3 Herren Misner, Thorne und Wheeler auszuleihen (oder zu kaufen, macht sich gut im Bücherregal  )! )!
Gruß,
Michi
Zuletzt bearbeitet von michifold am 31. Jul 2007 20:28, insgesamt einmal bearbeitet |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Jul 2007 18:06 Titel: isi1 Verfasst am: 31. Jul 2007 18:06 Titel: |
 |
|
Anregender Beitrag, Michi,
schreiben die drei Autoren auch etwas über die relativistische Elektrodynamik, die den Magnetismus als relativistischen Effekt der elektrischen Phänomene erklärt?
Diesen Effekt finde ich noch weitaus überraschender, wenn auch offenbar nicht alle Physiker daran glauben.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 31. Jul 2007 18:57 Titel: michifold Verfasst am: 31. Jul 2007 18:57 Titel: |
 |
|
Hallo Isi,
ich glaube, ich verstehe nicht ganz, was du meinst?
Aber die Autoren schreiben ausschließlich über relativistische Elektrodynamik. (Edit: Abgesehen davon, dass die restlichen 1000 Seiten natürlich die Gravitation, ART und ihre Effekte behandeln)
Und zwar erstens, um anhand der Elektrodynamik den Tensorbegriff zu veranschaulichen (das gelingt ihnen) und zweitens um anhand des Tensorbegriffs die Elektrodynamik zu erleuchten, was ihnen, wie ich finde besonders gut gelingt. Da sie nämlich zur Abwechslung nicht sagen, dass Tensoren indizierte Größen sind, die sich so und so transformieren, sondern dass es geometrische, anschauliche Objekte sind, die unabhängig von irgendwelchen Koordinatensystemen existieren, so wie z.B. der elektrische Feldstärketensor. Der nimmt nämlich je nach gewähltem Koordinatensystem (Inertialsystem) eine andere Form, manchmal mit B- und E-Feldeinträgen, manchmal nur mit E-Feldeinträgen.
Genauers entnimmst du dem Buch, lohnt sich wirklich!
Zuletzt bearbeitet von michifold am 31. Jul 2007 21:44, insgesamt einmal bearbeitet |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 31. Jul 2007 19:31 Titel: schnudl Verfasst am: 31. Jul 2007 19:31 Titel: |
 |
|
Ich finde diese Zusammenhänge auch immer wieder toll, aber die Transformationsgesetze der Felder werden eigentlich in jedem Buch über Elektrodynamik dargelegt, auch im (zumindest meinen) Jackson ist darüber ausgiebig die Rede.
Die Maxwellgleichungen sind bekanntermassen Lorentzinvariant, deswegen darf man sich auch über diese überraschenden Zusammenhänge nicht wundern.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Jul 2007 20:00 Titel: isi1 Verfasst am: 31. Jul 2007 20:00 Titel: |
 |
|
| michifold hat Folgendes geschrieben: | | Genauers entnimmst du dem Buch, lohnt sich wirklich! |
Gut, Michi, werde ich mir besorgen, Danke.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 31. Jul 2007 20:03 Titel: michifold Verfasst am: 31. Jul 2007 20:03 Titel: |
 |
|
Dass für E- und B-Felder bei Wechsel des Inertialsystems folgende gleichungen gelten, findet man natürlich in jedem Elektrodynamik-Buch:
 ) und und
 )
Die folgen natürlich einfach aus den Rechenregeln für Tensoren und dem Feldstärketensor.
Aber steht im Jackson tatsächlich, dass man die 2 dynamischen Maxwellgleichungen aus den statischen herleiten kann?
Ich hab den Jackson nicht da, kann natürlich sein, dass ich mich geirrt hab, und es ist auch schon ein Jahr her, dass ich da zuletzt reingschaut hab. Kannst ja vielleicht mal nachschaun. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 31. Jul 2007 21:39 Titel: schnudl Verfasst am: 31. Jul 2007 21:39 Titel: |
 |
|
| michifold hat Folgendes geschrieben: |
Aber steht im Jackson tatsächlich, dass man die 2 dynamischen Maxwellgleichungen aus den statischen herleiten kann?
|
Nein, so steht es nicht drinnen. Es wird im Jackson der umgekehrte Weg begangen, nämlich zuerst gezeigt, dass sich die Maxwellgleichungen aus einem Feldstärketensor herleiten (oder vielleicht besser: formulieren) lassen. Aus dem Verhalten eines Tensors unter Lorentztransformationen werden dann die Transfomationen der Feldkomponenten "hergeleitet".
Ich bin mir aber nicht so sicher, dass man von Deinem beschriebenen Zusammenhang von einer Herleitung der dynamischen Gleichungn sprechen kann, denn Du verwendest ja schon die bekannten Transformationsgesetze der Felder, und diese kann man, glaube ich, wiederum nur unter Zuhilfenahme eben dieser dynamischen Gleichungen beweisen, wie es Einstein in seiner Originalarbeit ab Seite 907 schön kurz und bündig vorgerechnet hat. Ich würde hier eher von Konsistenz als von einer Herleitung sprechen, auch wenn ich den Autoren die das behaupten, Misner/Thorne/Wheeler, nicht mal im Gedanken das Wasser reichen darf    - die wissen schon wovon sie reden, aber vielleicht ist dieser Zusammenhang im Werk ein bisserl plakativ vorgebracht, um die Begeisterung des Lesers zu wecken . - die wissen schon wovon sie reden, aber vielleicht ist dieser Zusammenhang im Werk ein bisserl plakativ vorgebracht, um die Begeisterung des Lesers zu wecken .
Trotzdem kann ich deine Begeisterung nachvollziehen und ich will sie in keiner Weise irgendwie zu schmälern versuchen. Ich bin selbst auch immer wieder aufs Neue fasziniert von diesen inneren Zusammenhängen. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 01. Aug 2007 00:12 Titel: michifold Verfasst am: 01. Aug 2007 00:12 Titel: |
 |
|
Hallo Schnudl,
Diese Transformationsgesetze für E- und B-Felder, sind wie ich geschrieben habe herleitbar alleine aus dem Feldstärketensor und dem Transformationsverhalten dessen Komponenten! keine Maxwellgleichungen werden benötigt!
Hier:
O.B.d.A nehmen wie einen Boost in z-Rtg.
 \gamma^2 F_{30}= F_{30}=E_z=E_{\Vert})
und jetzt eine senkrechte Komponente:

usw. für B-Felder und andere Boosts analog.
Du siehst, es kommen exakt die für die Herleitung benutzten Transformationgesetze raus, ohne Verwendung irgendwelcher Maxwellgleichungen. Alleine das Transformationsverhalten der Komponenten des Feldstärketensors führen zu den Transformationsgesetzen für E und B-Felder.
Du siehst wie unglaublich es ist, dass nie erwähnt wird und wie es schön ist, dass die 2 dynamischen Maxwellgleichungen aus den statischen folgen!! |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Aug 2007 07:37 Titel: schnudl Verfasst am: 01. Aug 2007 07:37 Titel: |
 |
|
Das stimmt schon, nur ist der Feldstärketensor ja nur eine elegantere Formulierung der schon bekannten Transformationstatsachen inclusive Maxwellgleichungen.
Ich will das ganze nun nicht unnötig breittreten, zumal ich es ja auch toll finde, was du gelesen hast. Ich denke nur: Wären zu damaligen Zeiten nur die beiden statischen Maxwellgleichungen bekannt gewesen, dann wäre niemend auf die Idee gekommen, E und B in eine gemeinsame Größe F hinein zu "packen", da es sich ja um zwei völlig verschiedene Grössen handeln würde: Das Reich der Elektrostatik wäre noch weitreichend getrennt von Reich des Magnetismus. Erst die kovariante Kopplung der beiden Felder E und B über die dynamischen Gleichungen hat diese tensorielle Formulierung meiner Ansicht nach nahegelegt. Natürlich hätte jemand die E und B Komponenten "in eine Matrix als Zahlenschema schreiben" können, aber wieso sollte daraus denn dein angesprochenes Transformationsverhalten (= der Tensorcharakter) folgen ? Dieses kann erst bei Vorhandensein aller Maxwellgleichungen gezeigt werden.
Ausserdem ergeben sich gerade aus diesem Feldstärketensor beide von dir angesprochenen Gleichungen:

enthält sowohl

und

deshalb kann man diesen nicht dazu verwenden, die dynamische Gleichung aus der statischen abzuleiten, da erstere schon in ihm enthalten ist und es ihn, ohne diese auch nicht geben würde.
Jetzt ist es aber schon ein wenig philosophisch, da wir über Metainhalte und weniger über Fakten diskutieren. Interessant finde ich es aber trotzdem.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 01. Aug 2007 08:01 Titel: isi1 Verfasst am: 01. Aug 2007 08:01 Titel: |
 |
|
| michifold hat Folgendes geschrieben: | Hallo Isi,ich glaube, ich verstehe nicht ganz, was du meinst?
Aber die Autoren schreiben ausschließlich über relativistische Elektrodynamik. .....Der nimmt nämlich je nach gewähltem Koordinatensystem (Inertialsystem) eine andere Form, manchmal mit B- und E-Feldeinträgen, manchmal nur mit E-Feldeinträgen. |
Das ist klar, Michi,
dass wenn ich z.B. als Elektron neben einem Elektronenstrahl her fliege, ich das Magnetfeld so rum oder anders herum sehe, je nachdem ob ich langsamer oder schneller fliege als der Elektronenstrahl. Fliege ich gleich schnell, sehe ich natürlich kein Magnetfeld des Elektronenstrahls.
Aber:
Sexl leitet in seinem Büchlein 'Raum - Zeit - Relativität' die Kräfte auf das parallel fliegende Elektron (die sonst das Magnetfeld erzeugt) ausschließlich aus der Lorentzkontraktion her. Er zeigt, dass sich das Magnetfeld nur als relativistischer Effekt des Coulombfeldes erweist.
So hatte ich das gemeint.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 01. Aug 2007 12:05 Titel: michifold Verfasst am: 01. Aug 2007 12:05 Titel: |
 |
|
@ Isi,
Danke für die Erleuterung! hab dich also wirklich nicht richtig verstanden :-)
Hab allerdings davon noch nichts gehört, werd mich aber mal im web informieren.
@schnudl,
Du hast damit Recht, dass der Feldstärketensor selbst schon (implizit) die Maxwellgleichungen enthält (allerdings nur die homogenen), jedoch sind zu seiner Motivation diese nicht nötig! Dazu braucht man nämlich nur die Lorentzkraft:
)
um das jetzt relativistisch zu "machen", multiplizieren wir beide Seiten mit gamma:
=e(u^0 \vec{E} + \vec{u} \times \vec{B}))
Wir sehen, dass die rechte Seite linear in u ist und vermuten, dass es eine lineare "Maschine" F (wie MTW schreiben) gibt so dass:
)
Zur Schreibweise: Vektoren, die keine zeitartige Komponente haben werden mit Pfeil drüber geschrieben, Vierervektoren werden Fett geschrieben (koordinatenfreie Darstellung).
Jetzt überlegt man sich noch was für die nullte Komponente. Wir wissen ja schon das im Viererimpuls dort die Energie steht:

da wir u und p als Vektoren auffassen, tragen also die Komponenten den Index oben, damit ergibt sich in Komponentenschreibweise:
 und für die Komponenten von F, die gewohnten Einträge. und für die Komponenten von F, die gewohnten Einträge.
Noch zu der Sache, dass der Feldstärketensor nur die homogenen Maxwellgleichungen enthält.
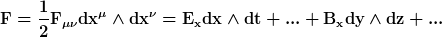 ist der Feldstärke als alternierende 2-Form geschrieben. ist der Feldstärke als alternierende 2-Form geschrieben.
bildet man davon die äußere Ableitung steht da:
 dx \wedge dy \wedge dz + (\partial_t B_x+\partial_y E_z-\partial_z E_y)dt \wedge dy \wedge dz+...)
Da tauchen, wie auch bei d*F alle linken Seiten der Maxwellgleichungen auf. Das dF=0 folgt aus der Tatsache, dass sich F=dA schreiben lässt und bekanntlich dd=0 ist.
Dass  weiß man nur, wenn man schon die Maxwellgleichungen kennt. Alleine aus dem Feldstärketensor folgt nicht, zumindest sehe ich nicht wie. weiß man nur, wenn man schon die Maxwellgleichungen kennt. Alleine aus dem Feldstärketensor folgt nicht, zumindest sehe ich nicht wie. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Aug 2007 13:10 Titel: schnudl Verfasst am: 01. Aug 2007 13:10 Titel: |
 |
|
Ich komme mir jetzt schon ein wenig blöd vor, aber, wie gesagt, ist alles was du schreibst völlig richtig, und heute schon fast Schulstoff, nur stelle ich mir eben vor, wir lebten in einer hypothetischen Zeit vor Maxwell, in der nur die statischen Gleichungen bekannt gewesen sein sollen (ich glaube, das war tatsächlich mal so):
Nun habe ich ziemliche Schwierigkeiten, mir vorzustellen, wie man mit diesem Wissen alleine (Magnetostatik und Elektrostatik), und vielleicht dem Wissen um die relativistische Mechanik auf den Tensor F gekommen wäre, der sich genau so transformiert, dass daraus die (noch unbekannten) dynamischen Maxwellgleichungen zwingend herleitbar sein sollen. Natürlich kann man den Zusammenhang mit dem Tensor F auch postulieren (... und vermuten, dass es eine lineare "Maschine" F gibt ...) und die darsu folgenden Konsequenzen überprüfen, aber das ist dann keine mathematische Herleitung, sondern eine empirisch zu bestätigende Tatsache. Natürlich: Sobald man den Tensor und seine Eigenschaften mal als gegeben hinnimmt, kann man natürlich alles daraus herleiten, was nur Spass macht und mathematisch daraus folgt. Aber das ist schon der zweite, weniger geniale Schritt.
Als gleichwertiges Beispiel kann man die Entdeckung des Verschiebungsterms durch Maxwell heranziehen. Dieser Term liess sich aus den damals bekannten Gleichungen genausowenig herleiten als man die dynamischen Gleichungen aus den statischen herleiten kann. Es war einfach eine geniale Entdeckung von Maxwell , die durch Experimente weitgehend bestätigt wurden, und daher als etwas "Neues" in die Physik eingegangen ist.
Oder die Dirac-Gleichung: Der Ansatz mit den Diracmatrizen ist zwar naheliegend, aber durch nichts als das Experiment zu rechtfertigen. Natürlich kann man im Nachhinein immer flapsig sagen "als plausiblen Ansatz wählen wir ...", da ja schon bekannt ist, dass er "stimmt".
Vielleicht haben wir eine Andere Auffassung darüber, was man als strenge Herleitung im Sinne einer mathematischen Konsequenz, oder als neuartig postuliertes Naturgesetz verstehen darf, bzw. worauf man überhaupt aufsetzen soll.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 01. Aug 2007 14:11 Titel: michifold Verfasst am: 01. Aug 2007 14:11 Titel: |
 |
|
Ich will dich auf keinen Fall nerven!
Ich versuchs mal auf den Punkt zu bringen:
1.Wenn wir annehmen, dass die spezielle Relativitätstheorie auf die Realität zutrifft, müssen die Naturgesetze unabhängig vom IS und damit die Gleichungen kovariant sein. Daraus schließen wir, dass die Gleichung der Lorentzkraft kovariant geschrieben werden kann. Die einfachst mögliche Form schaut so aus wie oben. Sie muss natürlich nicht richitg sein und es gibt keine Herleitung für die spezielle Form des Feldstärketensors. Aber, dass es so einen Tensor gibt folgt aus der Kovarianzannahme! Und damit steht auch das Transforamtionsverhalten seiner Komponenten fest.
Die einfachste kovariante Formulierung der Lorentzkraft, kann man jetzt mit Ockhams Rasiermesser als die physikalisch richtige postulieren.
2.Wenn wir jetzt sagen, dass wie nur die statischen Maxwellgleichungen, die Lorentzkraft und SRT haben, können wir doch jetzt die dynamischen mit Hilfe von 1.) mathematisch exakt, wie ganz oben geschehen, herleiten. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Aug 2007 14:23 Titel: schnudl Verfasst am: 01. Aug 2007 14:23 Titel: |
 |
|
Du nervst mich nicht, ich hoffe es trifft auch das Gegenteil zu...
Natürlich folgt aus dem richtigen Feldstärketensor die besagte Maxwellgleichung. Aber diese mathematische Herleitung (2. bei dir) ist eine Kinderei im Vergleich zu der Intuition, welche für die korrekte Aufstellung des Tensors überhaupt nötig ist (1.). Und dabei liess man sich bestimmt von allen Maxwellgleichungen leiten, und nicht nur von den statischen. Ohne die dynamischen Gleichungen käme man vermutlich gar nicht auf die Idee, dass Magnetismus (B-Feld) etwas mit Elektrik (E-Feld) zu tun hat, und würde "grundverschiedene" Entitäten nicht in eine Gleichung packen, so wie man ja auch nicht die starke Wechselwirkung in den Tensor mit hineinnimmt (zumindest nicht in dieser Form).
Deine Argumentaion kommt mir vor (ist nicht abwertend gemeint), als wenn man alle Postulate der Quantentheorie akzeptiert, und sich dann darüber begeistert, dass daraus die Unschärferelation folgt und zudem dann sagt, dass diese herleitbar ist. Vielmehr wurde an den Postulaten solange herumgedreht, bis sie sich in Einklang mit den Experimenten, also auch der Unschärferelation bringen liessen, was aber in den Lehrbüchern natürlich untergeht, da man die Zeit nicht hat, um die volle Geschichte aufzuarbeiten. Nur als Vergleich ...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 01. Aug 2007 15:37 Titel: michifold Verfasst am: 01. Aug 2007 15:37 Titel: |
 |
|
nein, mich nervst du auch nicht :-)
Was du in deinem ersten Abschnitt über die Motivation des Feldstärketensors schreibst stimmt meiner Meinung nach nicht: Es sind keine Maxwellgleichungen für die Motivation nötig!
Die Grundidee in dem Buch ist folgende: Felder, Kräfte, Geschwindigkeiten usw. sind geometrische Objekte,die unabhänig von Koordinatensystemen existieren und unverändert bleiben, wenn man von einem darstellenden Koordinatensystem auf ein anderes wechselt (Lorentztrafo). Diese geometrischen Objekte sind eben in mathematischer Sprache Tensoren. Deswegen dürfen nur sie in Gleichungen stehen, die kovariant(=lorentz-invariant) sein sollen.
Wenn ich also die Lorentzkraft in ein solches geometrisches Objekt verwandeln will, muss ich versuchen alle Felder, Kräfte, Geschwindigkeiten, usw. in Tensoren zu verwandeln. Die Vorgehensweise ist natürlich nicht ganz klar, aber wie ich finde relativ verständlich so wie sie im Buch steht und wie ich sie hier im Forum wiedergegeben habe.
1. Die neue Gleichung muss 4 Komponenten haben, da es sich um ein Kraft handelt, also links und rechts muss ingesamt ein Tensor 1. Stufe stehen
2. Für Impuls, Zeit und Geschwindigkeit wissen wir, wie man 4er Vektoren draus machen kann, das tun wir
3.Wir stellen fest das die rechte Seite linear in den Komponenten von u ist. Und damit ist das Objekt F, in welchem wir E und B-Feldkomponenten zusammengefasst haben, ein Tensor, und damit ist die Gleichung kovariant!
Wir sind also nur deswegen auf die Idee gekommen E und B Felder, die zuerst nichts miteinander zu tun haben, außer, dass sie beide irgendwelche Kräfte auf Ladungen ausüben, in einem Objekt F zusammenzufassen, da so eine experimentell bestätige Gleichung kovariant formuliert werden konnte. Und das war unser eigentliches Ziel.
Ich finde nicht, dass wir hier wie in der Quantenmechanik, eine Reihe unverständlicher mathematischer Postulate haben und daraus *welchwunder* die Unbestimmtheitsrelation herleiten können.
Vielmehr haben wir hier in Worte fassbare und verstehbare Postulate, die nicht extra irgendwie hingemurkst wurden. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 01. Aug 2007 16:07 Titel: schnudl Verfasst am: 01. Aug 2007 16:07 Titel: |
 |
|
Ja, im Nachhinein ist es leicht diese Forderungen 1-3 zu stellen. Die Geschichte war aber anders, und es führte der Weg u.A. über alle Maxwellgleichungen und der Erkenntnis dass diese lorentzivariant sind zu den heute bekannten, kovariant formulierten Naturgesetzmässigkeiten. Einsteins Arbeit heisst ja nicht umsonst "zur Elektrodynamik bewegter Körper" und nicht "Mechanik bewegter Körper". Ich glaube dass gerade die Maxwellgleichungen ein wesentlicher Meilenstein in dieser Richtung waren, da diese schon von Haus aus lorentzinvariant sind.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 01. Aug 2007 17:37 Titel: isi1 Verfasst am: 01. Aug 2007 17:37 Titel: |
 |
|
Es ist eine Freude, Eurerer Diskussion zu folgen - wenn ich auch zeitweise mit den Ohren schlackere :)
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 01. Aug 2007 18:12 Titel: michifold Verfasst am: 01. Aug 2007 18:12 Titel: |
 |
|
Aber bei der Quantenmechanik ist es doch so, dass die historischen Gegebenheiten überhaupt keinen Einfluss auf die Lehrbuchquantenmechanik haben:Da hat man im Nachhinen 5 abstrakte mathematische Postulate aufgestellt!
Deswegen wundert mich, dass man mit der Elektrodynamik nicht auch so verfährt.
Wieso 4 Maxwellgleichungen, wenn es 2 tun?
@isi
schön, dass du auch Spaß hast 
hab im Internet nichts gefunden, aber die Unibibliothek hat das Buch. Werds mir demnächst mal ausleihen! |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 02. Aug 2007 10:37 Titel: schnudl Verfasst am: 02. Aug 2007 10:37 Titel: |
 |
|
Nachdem ich über deine Aussagen nicht schlafen konnte, hab ich mir es nochmals überlegt. Leider bin ich nicht sehr sattelfest im Tensorkalkül, aber immerhin vermag ich jetzt Deine Begeisterung nachzuvollziehen.
Denn die Lorentzkraft kann man, wie du schon sagtest, formal vierdimensional schreiben als

Hier braucht man noch keinen Tensorcharakter von F annehmen. Wenn man aber davon ausgeht, dass die linke Seite ein Tensor ist, und auch die Vierergeschwindigkeit U, dann tut man gut daran, dies auch für F zu fordern (ist dies richtig ?). Davon abgesehen ist F vollständig durch die B und E Komponenten (wie üblich) definiert.
Deine Überlegungen in Tensorschreibweise sind nun:
Im System S' gilt sicher die erste inhomogene (statische) Maxwellgleichung

oder

Der Übergang von S auf S' wird vermittelt durch

und

Das ergibt

Da diese Relation für alle Transformationen gelten muss, hat man

Das sind aber genau die beiden inhomogenen Maxwellgleichungen (MGL).
Ähnliches kann man (genau wie du, nur in Tensorschreibweise) für die homogenen MGL tun.
Du hast also Recht, dass man über die statischen MGL auf die dynamischen kommt, wenn man dem F in der Lorentzkraft Tensorcharakter zuschreibt.
Meine Frage ist nun:
Ist dies (was ich oben mit dem Fragezeichen hervorhob) ein strenger Schluss?
Oder könnte die Matrix F(i,j) vielleicht u.U. auch keinen Tensorcharakter haben, und die linke Seite (die Änderung des Impulses) doch ?
Wenn man den Tensorcharakter aber erst extra fordern muss, dann braucht man wiederum alle Maxwellgleichungen.
Jedenfalls ist die Viererformulierung in sich konsistent... Es wäre vielleicht besser, nicht von einem Feld E oder B zu sprechen, sondern von einem koordinatensystemunabhängigen Feldstärketensor F, der beide Entitäten enthält, aber dessen konkreter Aufbau (die Darstellung) vom Koordinatensystem abhängt.
Folgt aus
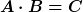
automatisch, dass A ein Tensor ist, wenn B und C Tensoren sind ?
Das ist meines Erachtens der kritische Punkt in Deinen Überlegungen.
Die Frage ist vielleicht ein wenig dilletantisch gestellt, aber wie gesagt, ist der Tensorkalkül nicht meine Stärke, da ich keine tiefen Einsichten darin besitze. Vielleicht lohnt sich das mal zu lernen...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 02. Aug 2007 13:52 Titel: michifold Verfasst am: 02. Aug 2007 13:52 Titel: |
 |
|
Hallo Schudl,
ich wollte dich nicht schalflos machen :-), finds aber toll, dass du nochmal drüber nachgedacht hast!
Deine Rechung scheint richtig zu sein, nur dass
^{\epsilon}_{\ \alpha} \partial_{\epsilon})
Soll heißen, die Differentialoperatoren transformieren sich genau invers zu den Komponenten eines Vektors. Aber das hast du ja dann in der Rechung trotzdem richtig gemacht, wo dann das Kronecker-Delta rauskommt.
So und jetzt zu dem wichtigen Punkt! ja, es ist wirklich zwingend, dass F Tensor sein muss und man muss es nicht fordern:

Ein Tensor ist nämlich eine (p+q)-lineare Abbildung die p Vektoren und q Kovektoren auf eine Zahl abbildet. Genau das haben wir hier, nur dass wir nicht 2 Vektoren, bzw. in deiner obigen Formulierung 2 Kovektoren einsetzen, sondern nur einen, aber das spielt keine Rolle. Die Linearität ist wichtig und die haben wir: Der Kovektor  wird linear auf den Vektor wird linear auf den Vektor  abgebildet, was nur ein (0,2)-Tensor abgebildet, was nur ein (0,2)-Tensor
 bewriken kann: bewriken kann:
( dx^{\mu})= F^{\alpha \beta} u_{\mu} \partial_{\alpha} \delta^{\mu}_{\beta}= F^{\alpha \mu} u_{\mu} \partial_{\alpha})
wobei ich hier den Vorfaktor e/(mc) in F reingezogen hab.
Und damit ergibt sich aus der Annahme, dass sich Naturgesetze kovariant formulieren lassen, der Feldstärketensor als das physikalische, geometrische Objekt, das das elektromagentische Feld beschreibt.
Und mit den anschließenden "Kindereien" können wir also die zwei dynamischen Maxwellgleichungen aus den statischen Herleiten!
Der einzige nicht ganz saubere, bzw. auch nicht eindeutige Schritt ist die "Kovariantisierung" der Lorentzkraft. Aber das ist meiner Meinung nach die einfachst mögliche kovariante Form der Lorentzkraft und damit bis auf experimentelle Falsifizierung die richtige! Und es ist natürlich willkürlich, ob ich in F den Faktor 1/c oder e/c reinschiebe oder nicht (Wenn ich der Faulheit halber nicht sowie c=1 gesetzt hab)
Wenn du mit Tensoren nicht nur rechnen, sondern wirklich eine Vorstellung davon entwickeln willst (bei mir funtkioniert das langsam sogar), kann ich dir "Gravitation" nur empfehlen. Dort siehst du sogar Abbildungen vom Feldtärketensor! (natürlich mit unterdrückter vierter Dimension  ). ). |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 02. Aug 2007 16:32 Titel: schnudl Verfasst am: 02. Aug 2007 16:32 Titel: |
 |
|
| Zitat: | Deine Rechung scheint richtig zu sein, nur dass
|
Hier hab ich bei

Die Indizes mit dem g Tensor nach unten gezogen, und einen kovarianten daraus gemacht:

mit

Mit den Punkten wird das vielleicht klarer.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
michifold
Anmeldungsdatum: 21.10.2006
Beiträge: 34
|
 michifold Verfasst am: 02. Aug 2007 17:15 Titel: michifold Verfasst am: 02. Aug 2007 17:15 Titel: |
 |
|
Wir haben beide Recht:

Damit bekommen wir mit deiner Indexgymnastik und Matrixmultiplikation:

was natürlich genau einer inversen Lorentztrafo entspricht.
also
^{\mu}_{\ \nu}=\Lambda_{\mu}^{\ \nu})
Hmm, jetzt wär eigentlich alles gesagt. Nur schade, dass wahrscheinlich allen, die nicht zufällig mal ins Gravitation schaun, oder so schlau sind selbst auf die Zusammehänge zu kommen, dieser Einblick verwährt bleibt.
Aber vielleicht lesen ja viele diesen Thread und werden erleuchtet  |
|
 |
|
|
















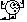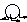 ), frage mich, ob das wohl auch für die elektrostatische Maxwellgleichung
), frage mich, ob das wohl auch für die elektrostatische Maxwellgleichung
 ) zu finden ist?
) zu finden ist?


