| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 21. Jan 2021 12:11 Titel: Lokale Lorentzinvarianz und allgemeine Kovarianz in der ART Corbi Verfasst am: 21. Jan 2021 12:11 Titel: Lokale Lorentzinvarianz und allgemeine Kovarianz in der ART |
 |
|
Was genau bedeutet die lokale Lorentzinvarianz in der ART und was genau bedeutet die Invarianz unter allgemeinen Koordinatentransformationen in der ART?
Unter ersterem verstehe ich bisher, dass man an einem beliebigen Punkt P immer Koordinaten wählen so dass der metrische Tensor g an diesem Punkt mit der Minkowski-Metrik übereinstimmt und eine anschließende Lorentztransformation der Koordinaten führt die Minkowski-Metrik an diesem Punkt wieder in eine Minkowski-Metrik über.
Unter Zweiterem verstehe ich, dass ich die Gesetze in der ART, egal welches Koordinatensystem ich verwende, auf die selbe Weise hinschreiben kann. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 21. Jan 2021 15:27 Titel: TomS Verfasst am: 21. Jan 2021 15:27 Titel: |
 |
|
Die Invarianz unter allgemeinen Koordinatentransformationen bzw. Diffeomorphismen besagt ...
1) ... dass für die pseudo-Riemannsche Mannigfaltigkeit M Karten (Koordinatensysteme mit Koordinatenfunktionen) existieren, so dass Punkte P aus M bijektiv und (k-fach) stetig differenzierbar auf Koordinaten abgebildet werden
 )
2) ... dass die Umkehrfunktionen ebenfalls bijektiv und (k-fach) stetig differenzierbar sind und damit Koordinatentransformationen
 \to P \to y^\mu(P) )
möglich sind.
3) ... dass die Gleichungen der ART unter (2) forminvariant sind.
Die Invarianz unter lokalen Lorentztransformationen versteht man am besten im Tangentialraum; d.h. ...
1) ... dass in jeden Punkt P der pseudo-Riemannschen Mannigfaltigkeit M ein flacher = minkowskischer Tangentialraum T_P mit Vierbeinfeldern


existiert wobei die zweite Gleichung das Vektorfeld im flachen Tangentialraum bezeichnet.
2) ... dass diese Vierbeine lokal beliebig gewählt und mittels lokaler Lorentztransformationen rotiert werden können:

und dass dies analog für Tensoren im Tangentialraum gilt
Siehe hier: https://arxiv.org/pdf/gr-qc/9712019.pdf
Interessant ist, dass diese Invarianz unter lokalen Lorentztransformationen direkt einer lokalen Eichsymmetrie entspricht.
Technisch wird index_razor das sicher präzisieren :-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Jan 2021 19:49, insgesamt 2-mal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. Jan 2021 18:54 Titel: index_razor Verfasst am: 21. Jan 2021 18:54 Titel: |
 |
|
Wesentlich anders würde ich das auch nicht formulieren. Die "allgemeine Koordinateninvarianz" bedeutet für mich, daß die Raumzeit eine differenzierbare Mannigfaltigkeit ist, also im wesentlichen 1) und 2).
Unter lokaler Lorentzinvarianz verstehe ich die letztlich auf dem Äquivalenzprinzip beruhende Tatsache, daß der Tangentialraum ein Minkowskiraum ist. Das ist soweit ich sehe äquivalent dazu, daß man auf der Raumzeit Felder von Lorentzbasen errichten kann, und die Menge aller dieser Felder eine Mannigfaltigkeit bildet, die lokal diffeomorph zu U x SO(3,1) ist, wobei U eine offene Menge in der Raumzeit ist. Das ist also analog zu den Verhältnissen in einer Eichtheorie mit der Lorentzgruppe als "Eichgruppe".
Das einzige, wobei ich mir unsicher bin, ist die "Forminvarianz" der Gleichungen. Ich halte den Begriff nicht für besonders nützlich. Soweit ich ihn verstehe, ist damit entweder eine bestimmte Symmetrie gemeint (die normalerweise in der ART nicht vorliegt), oder die Tatsache, daß die Gleichungen Beziehungen zwischen Tensoren ausdrücken. Letzteres hat an sich aber nicht viel mit einer "Invarianz" zu tun und außerdem sehe ich nicht ganz die Notwendigkeit, dafür einen extra Begriff einzuführen. (Rein inhaltlich habe ich aber keine Einwände dagegen.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 21. Jan 2021 19:43 Titel: TomS Verfasst am: 21. Jan 2021 19:43 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Wesentlich anders würde ich das auch nicht formulieren. |
Danke ;-)
| index_razor hat Folgendes geschrieben: | | Das einzige, wobei ich mir unsicher bin, ist die "Forminvarianz" der Gleichungen. Ich halte den Begriff nicht für besonders nützlich. Soweit ich ihn verstehe, ist damit entweder eine bestimmte Symmetrie gemeint (die normalerweise in der ART nicht vorliegt), oder die Tatsache, daß die Gleichungen Beziehungen zwischen Tensoren ausdrücken. Letzteres hat an sich aber nicht viel mit einer "Invarianz" zu tun und außerdem sehe ich nicht ganz die Notwendigkeit, dafür einen extra Begriff einzuführen. (Rein inhaltlich habe ich aber keine Einwände dagegen.) |
Ich habe auch darüber nachgedacht.
Ich denke, zunächst sind Forminvarianz und Kovarianz nicht ganz das selbe. Wenn man eine Theorie im Kontext der SRT mittels Vierer-Vektoren und -Tensoren formuliert, dann ist sie (manifest) kovariant. Wenn man die selbe Theorie mittels Dreier-Vektoren formuliert, dann ist sie natürlich immer noch Lorentz-invariant, jedoch nicht mehr (manifest) kovariant.
Wenn analog in der Newtonschen Mechanik eine Transformation so wirkt, dass sich die Lagrangefunktion um eine totale Zeitableitung ändert, dann ist diese offenbar nicht forminvariant, jedoch bzgl. Galilei-Transformationen immer noch (manifest) kovariant, und Observable sind immer noch invariant.
Die Newtonsche Mechanik ist invariant unter zeitunabhängigen Galilei-Transformationen; eine Lagrangefunktion ist nicht forminvariant unter zeitabhängigen Galilei-Transformationen - siehe Corioliskraft; die Observablen sind diesbzgl. aber dennoch invariant.
Andere Beispiele: Hamiltonsche Formulierung einer Quantenfeldtheorie oder der ART - nicht kovariant, jedoch Lorentz-invariant bzw. im Falle der ART diffeomorphismen-invariant und lokal Lorentz-invariant. Quantisierung der QCD inkl. quantenmechanischer Eichfixierung - diesbgl. nicht forminvariant (gauge fixing term, ggf. Fadeev-Popov-Felder, jedoch dennoch eichinvariant).
Von daher sollten wir (3) besser streichen. Es ist ein etwas anderer Begriff für die "manifeste" Kovarianz, rein technisch, und nicht zwingend notwendig. Fehlende Kovarianz oder Forminvarianz sagt insbs. nichts über die Invarianz von Observablen, und nur das ist letztlich der relevante physikalische Gehalt der Theorie.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Jan 2021 19:45 Titel: index_razor Verfasst am: 23. Jan 2021 19:45 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Wesentlich anders würde ich das auch nicht formulieren. |
Danke ;-)
|
Gern geschehen.;-)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Das einzige, wobei ich mir unsicher bin, ist die "Forminvarianz" der Gleichungen. Ich halte den Begriff nicht für besonders nützlich. Soweit ich ihn verstehe, ist damit entweder eine bestimmte Symmetrie gemeint (die normalerweise in der ART nicht vorliegt), oder die Tatsache, daß die Gleichungen Beziehungen zwischen Tensoren ausdrücken. Letzteres hat an sich aber nicht viel mit einer "Invarianz" zu tun und außerdem sehe ich nicht ganz die Notwendigkeit, dafür einen extra Begriff einzuführen. (Rein inhaltlich habe ich aber keine Einwände dagegen.) |
Ich habe auch darüber nachgedacht.
Ich denke, zunächst sind Forminvarianz und Kovarianz nicht ganz das selbe.
|
Das denke ich auch. Statt von Forminvarianz rede ich wie gesagt lieber einfach von Invarianz. Denn das Invariante ist sinnvollerweise irgendein Objekt und nicht die "Form" eines Objekts, was auch immer das genau sein soll. Dann muß man nur noch die Frage beantworten: "welches Objekt?" Da gibt es mehrere Möglichkeiten, z.B. Lagrangefunktion, Wirkung oder Bewegungsgleichungen. Invarianz der Lagrangefunktion impliziert Invarianz der Wirkung und der Bewegungsgleichungen, aber jeweils nicht umgekehrt. (Ich denke im Zusammenhang mit Gleichungen reden viele Lehrbücher lieber von "Forminvarianz". Aber die Gleichungen kann man in diesem Kontext mit ihrer Lösungsmenge identifizieren. Das ist wieder eine Mannigfaltigkeit und damit ein Objekt, über dessen Invarianz man sinnvoll reden kann.) Invarianz der Wirkung ist hier wahrscheinlich die wichtigste Eigenschaft wegen des Zusammenhangs zu Erhaltungsgrößen. In all diesen Fällen geht es um die Invarianz unter (aktiven) Transformationen von Raum und Zeit und den davon abhängigen Größen (z.B. dem elektromagnetischen Feld).
Mit einer "Invarianz" unter Koordinatenwechseln hat das ganz also erstmal nichts zu tun. Die Tatsache, daß man die Maxwellgleichungen in der Form

schreiben kann, die in jedem Koordinatensystem gilt, ändert nichts daran, daß sie im allgemeinen nur invariant unter Poincaretransformationen (oder höchstens invariant unter der konformen Gruppe und der dualen Transformation  ) ist. ) ist.
Ganz unten bringst du Eichtheorien ins Spiel. Dabei fällt mir ein, daß "allgemeine Kovarianz" im Zusammenhang mit Hamiltonschen System manchmal auch in dem Sinne verstanden wird, daß die Zeit selbst eine kanonische Variable ist. Diese Eigenschaft haben im Prinzip alle Eichtheorien, da die Lösungen ihrer Gleichungen nur bis auf eine oder mehrere beliebige Funktionen der Zeit eindeutig definiert sind. In der ART ist das ganz offensichtlich so.
Ich denke der Punkt ist nun, daß allgemeine Kovarianz in diesem Sinne im Falle der ART zur Folge hat (?), daß aktive Diffeomorphismen zu den Eichsymmetrien der Theorie gehören. Es geht also nicht um eine Invarianz unter Koordinatentransformation, die man für so ziemlich jede Theorie hinbekommen kann, und in diesem Fall auch nicht darum, daß die Lorentzgruppe "Eichgruppe" des Frame-Bündels ist (was wir als lokale Lorentzinvarianz bezeichnet haben), sondern um die Tatsache, daß die Gruppe aller Diffeomorphismen der Raumzeit auf sich selbst Eichsymmetrien der Einsteinschen Feldgleichungen sind.
Frage: worin besteht der Zusammenhang dieser Eichinvarianz zu der Tatsache, daß die Feldgleichungen Tensorgleichungen sind? Und spielt es eine Rolle, daß der Einsteintensor nur von der Metrik und ihren Ableitungen abhängt? Wald versteht unter "allgemeiner Kovarianz" die etwas nebulöse Aussage, daß die Metrik die einzige zur Raumzeit gehörige Größe ist, die in den Naturgesetzen vorkommen darf. Deshalb vermute ich, daß hier irgendein Zusammenhang bestehen könnte, der sich mir nicht ganz erschließt.
| Zitat: |
Wenn man eine Theorie im Kontext der SRT mittels Vierer-Vektoren und -Tensoren formuliert, dann ist sie (manifest) kovariant. Wenn man die selbe Theorie mittels Dreier-Vektoren formuliert, dann ist sie natürlich immer noch Lorentz-invariant, jedoch nicht mehr (manifest) kovariant.
|
Ja, so sehe ich das auch.
| Zitat: |
Wenn analog in der Newtonschen Mechanik eine Transformation so wirkt, dass sich die Lagrangefunktion um eine totale Zeitableitung ändert, dann ist diese offenbar nicht forminvariant, jedoch bzgl. Galilei-Transformationen immer noch (manifest) kovariant, und Observable sind immer noch invariant.
Die Newtonsche Mechanik ist invariant unter zeitunabhängigen Galilei-Transformationen; eine Lagrangefunktion ist nicht forminvariant unter zeitabhängigen Galilei-Transformationen - siehe Corioliskraft; die Observablen sind diesbzgl. aber dennoch invariant.
|
Hier hängst du mich langsam ab. Die Gleichungen der Newtonschen Mechanik sind im allgemeinen nicht invariant unter zeitabhängigen Galileitransformationen. Sie sind allerdings, genau wie die Maxwellgleichungen, "kovariant" in dem Sinne, daß sie unabhängig vom Koordinatensystem gelten. (Sie sind allerdings wohl nicht "forminvariant" unter solchen Transformationen, weil z.B. die Kraft ) kein gewöhnliches Tensorfeld ist.) kein gewöhnliches Tensorfeld ist.)
Die Observablen sind normalerweis eigentlich auch nicht invariant, nicht mal unter Symmetrien der Theorie, wie in diesem Fall den Galileitransformationen. Jede Transformation ändert die Anfangsbedingungen und damit auch den Wert von Funktionen ) zu einem bestimmten Zeitpunkt. (Abgesehen von offensichtlichen Ausnahmen, wie Erhaltungsgrößen unter Zeittranslationen, etc.) zu einem bestimmten Zeitpunkt. (Abgesehen von offensichtlichen Ausnahmen, wie Erhaltungsgrößen unter Zeittranslationen, etc.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 23. Jan 2021 22:30 Titel: TomS Verfasst am: 23. Jan 2021 22:30 Titel: |
 |
|
Den von dir angesprochen Punkt bzgl. der Diffeomorphismen als lokale Eichsymmetrie verstehe ich auch nicht.
Zu den zeitabhängigen Galileitransformationen: klar, die Theorie ist diesbzgl. offenbar nicht forminvariant. Aber dennoch sind derartige Transformationen als Koordinatentransformationen möglich - siehe Rechnungen im rotierenden Bezugsystem.
Was du damit meinst, dass “die Observablen normalerweise auch nicht invariant unter Symmetrien der Theorie sind” verstehe ich nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 24. Jan 2021 12:24 Titel: TomS Verfasst am: 24. Jan 2021 12:24 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | In all diesen Fällen geht es um die Invarianz unter (aktiven) Transformationen von Raum und Zeit und den davon abhängigen Größen (z.B. dem elektromagnetischen Feld). |
Nach etwas Literaturstudium bin ich immer noch nicht so viel schlauer. Je mehr ich lese, desto mehr verwirrt mich die Unterscheidung zwischen aktiven und passiven Diffeomorphismen. Außerdem habe ich den Eindruck, dass Mathematiker gerne Diffeomorphismen als Transformationen zwischen verschiedenen Mannigfaltigkeiten betrachten, während Physiker sie auf der selben Mannigfaltigkeit verstehen.
Evtl.. hilft zunächst das hier weiter:
https://arxiv.org/abs/gr-qc/9712019v1
Lecture Notes on General Relativity
Sean M. Carroll
You will often hear it proclaimed that GR is a “diffeomorphism invariant” theory. What this means is that, if the universe is represented by a manifold M with metric gμν and matter fields ψ, and φ : M → M is a diffeomorphism, then the sets
 )
and
)
represent the same physical situation. Since diffeomorphisms are just active coordinate transformations, this is a highbrow way of saying that the theory is coordinate invariant. Although such a statement is true, it is a source of great misunderstanding, for the simple fact that it conveys very little information. Any semi-respectable theory of physics is coordinate invariant, including those based on special relativity or Newtonian mechanics; GR is not unique in this regard. When people say that GR is diffeomorphism invariant, more likely than not they have one of two (closely related) concepts in mind: the theory is free of “prior geometry”, and there is no preferred coordinate system for spacetime. The first of these stems from the fact that the metric is a dynamical variable, and along with it the connection and volume element and so forth. Nothing is given to us ahead of time, unlike in classical mechanics or SR. As a consequence, there is no way to simplify life by sticking to a specific coordinate system adapted to some absolute elements of the geometry. This state of affairs forces us to be very careful; it is possible that two purportedly distinct configurations (of matter and metric) in GR are actually “the same”, related by a diffeomorphism. In a path integral approach to quantum gravity, where we would like to sum over all possible configurations, special care must be taken not to overcount by allowing physically indistinguishable configurations to contribute more than once. In SR or Newtonian mechanics, meanwhile, the existence of a preferred set of coordinates saves us from such ambiguities. The fact that GR has no preferred coordinate system is often garbled into the statement that it is coordinate invariant (or “generally covariant”); both things are true, but one has more content than the other.
Der hervorgehobene Teil bringt uns zu
| index_razor hat Folgendes geschrieben: | Ich denke der Punkt ist nun, daß allgemeine Kovarianz in diesem Sinne im Falle der ART zur Folge hat (?), daß aktive Diffeomorphismen zu den Eichsymmetrien der Theorie gehören. Es geht also nicht um eine Invarianz unter Koordinatentransformation, die man für so ziemlich jede Theorie hinbekommen kann, und in diesem Fall auch nicht darum, daß die Lorentzgruppe "Eichgruppe" des Frame-Bündels ist (was wir als lokale Lorentzinvarianz bezeichnet haben), sondern um die Tatsache, daß die Gruppe aller Diffeomorphismen der Raumzeit auf sich selbst Eichsymmetrien der Einsteinschen Feldgleichungen sind.
|
Siehe jedoch hier:
http://philsci-archive.pitt.edu/834/1/gr_gauge.pdf
Gravity and Gauge Theory
Steven Weinstein
Perhaps the first thing to note about general relativity is that the diffeomorphism group is not the characteristic group of a group bundle at all. Recall that in a gauge theory, a copy of the gauge group sits over each point of the manifold, and gauge transformations induce changes in the connection (the gauge field) at each point, changes that nonetheless leave the physics at the point unchanged. Diffeomorphisms are a completely different sort of beast — there is no copy of the diffeomorphism group sitting over each point of the manifold, nor is the diffeomorphism group the product G × M of some other internal group G with the manifold M.
Rather than inducing changes in the field at a point, diffeomorphisms map points x to other [other] points x*, and induce changes in the fields (metric tensor, Riemann tensor, etc.) by mapping the fields from one point to another [das klingt nach einer Sichtweise entsprechend der aktiven Diffeomorphismen] ...
... general relativity [is] fundamentally relational in nature. For example, if we have a general relativistic model (M,gαβ,Fαβ), where gαβ is the metric tensor and Fαβ is the Maxwell tensor, then a typical prediction of the model will be of the form ìthe curvature of spacetime is so-and-so where the electromagnetic field has such-and-such value.
Die Schlussfolgerung ist, dass die Diffeomorphismeninvarianz zwar ebenfalls “fixiert” werden muss, um diffeomorphe Konfigurationen nicht mehrfach zu zählen, dass Diffeomorphismeninvarianz jedoch im mathematischen Sinne keine Eichinvarinanz ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Jan 2021 13:21 Titel: index_razor Verfasst am: 24. Jan 2021 13:21 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Zu den zeitabhängigen Galileitransformationen: klar, die Theorie ist diesbzgl. offenbar nicht forminvariant. Aber dennoch sind derartige Transformationen als Koordinatentransformationen möglich - siehe Rechnungen im rotierenden Bezugsystem.
|
Schon. Allerdings sind in allen Theorien eben so ziemlich alle Arten von Koordinatentransformationen möglich. Daraus folgt m.E. nicht viel. (Das scheint ja auch Carroll zu behaupten, obwohl ich glaube, daß Diffeomorphismeninvarianz etwas anderes ist.)
| Zitat: |
Was du damit meinst, dass “die Observablen normalerweise auch nicht invariant unter Symmetrien der Theorie sind” verstehe ich nicht. |
Die Energie 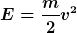 z.B. ist doch keine invariante Funktion unter Galileitransformationen. z.B. ist doch keine invariante Funktion unter Galileitransformationen.
Zum Rest etwas später. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Jan 2021 15:20 Titel: index_razor Verfasst am: 24. Jan 2021 15:20 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | In all diesen Fällen geht es um die Invarianz unter (aktiven) Transformationen von Raum und Zeit und den davon abhängigen Größen (z.B. dem elektromagnetischen Feld). |
Nach etwas Literaturstudium bin ich immer noch nicht so viel schlauer. Je mehr ich lese, desto mehr verwirrt mich die Unterscheidung zwischen aktiven und passiven Diffeomorphismen. Außerdem habe ich den Eindruck, dass Mathematiker gerne Diffeomorphismen als Transformationen zwischen verschiedenen Mannigfaltigkeiten betrachten, während Physiker sie auf der selben Mannigfaltigkeit verstehen.
|
Unter "passiven" Transformationen verstehe ich einfach Kartenwechsel auf derselben Mannigfaltigkeit M. Eine aktive Transformation ist eine glatte Abbildung  oder auch oder auch  . Letztere sind hier m.E. das nützlichere Konzept, denn "Invarianz unter passiven Transformationen" ist ziemlich bedeutungslos. Potentiell verwirrend ist, daß, wenn man alle Situationen auf M immer durch die Linse einer lokalen Karte betrachtet, der Unterschied zwischen Kartenwechslen auf M und Diffeomorphismen . Letztere sind hier m.E. das nützlichere Konzept, denn "Invarianz unter passiven Transformationen" ist ziemlich bedeutungslos. Potentiell verwirrend ist, daß, wenn man alle Situationen auf M immer durch die Linse einer lokalen Karte betrachtet, der Unterschied zwischen Kartenwechslen auf M und Diffeomorphismen  etwas verschwimmt. etwas verschwimmt.
| Zitat: |
Evtl.. hilft zunächst das hier weiter:
https://arxiv.org/abs/gr-qc/9712019v1
Lecture Notes on General Relativity
Sean M. Carroll
You will often hear it proclaimed that GR is a “diffeomorphism invariant” theory. What this means is that, if the universe is represented by a manifold M with metric gμν and matter fields ψ, and φ : M → M is a diffeomorphism, then the sets
 )
and
)
represent the same physical situation. Since diffeomorphisms are just active coordinate transformations, this is a highbrow way of saying that the theory is coordinate invariant.
|
Das übersieht m.E. ein wichtiges Detail: "The same physical situation" bedeutet nicht nur, daß wir für jedes Ereignis x umkehrbar eindeutig ein Ereignis ) definieren können und für jedes Feld definieren können und für jedes Feld  ein "push-forward/pull-back"-Feld ein "push-forward/pull-back"-Feld  , etc. Es bedeutet auch, daß , etc. Es bedeutet auch, daß  wiederum Lösungen derselben Gleichungen sind wie vorher. Damit sind wir bei Symmetrien der Gleichungen angelangt. Und das ist etwas völlig anderes als Koordinateninvarianz. Es bedeutet im Falle von Eichinvarianz, daß diese Gleichungen bestimmte Identitäten erfüllen müssen. Solche Identitäten gibt es überhaupt nicht in der Newtonschen Mechanik, obwohl sie ebenso Koordinateninvariant ist, wie die ART. Im Fall der Maxwellgleichungen gibt es nur die Identität wiederum Lösungen derselben Gleichungen sind wie vorher. Damit sind wir bei Symmetrien der Gleichungen angelangt. Und das ist etwas völlig anderes als Koordinateninvarianz. Es bedeutet im Falle von Eichinvarianz, daß diese Gleichungen bestimmte Identitäten erfüllen müssen. Solche Identitäten gibt es überhaupt nicht in der Newtonschen Mechanik, obwohl sie ebenso Koordinateninvariant ist, wie die ART. Im Fall der Maxwellgleichungen gibt es nur die Identität  , die aus der U(1)-Invarianz folgt. Es gibt keine Identitäten für "Diffeomorhismeninvarianz", obwohl die Maxwellgleichungen vollkommen invariant unter beliebigen Koordinatentransformationen sind. , die aus der U(1)-Invarianz folgt. Es gibt keine Identitäten für "Diffeomorhismeninvarianz", obwohl die Maxwellgleichungen vollkommen invariant unter beliebigen Koordinatentransformationen sind.
Koordinateninvarianz enthält wenig Information, das stimmt. Diffeomorphismeninvarianz der Feldgleichungen enthält Information, wie man daran erkennt, daß nicht alle Gleichungen sie haben.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Ich denke der Punkt ist nun, daß allgemeine Kovarianz in diesem Sinne im Falle der ART zur Folge hat (?), daß aktive Diffeomorphismen zu den Eichsymmetrien der Theorie gehören. Es geht also nicht um eine Invarianz unter Koordinatentransformation, die man für so ziemlich jede Theorie hinbekommen kann, und in diesem Fall auch nicht darum, daß die Lorentzgruppe "Eichgruppe" des Frame-Bündels ist (was wir als lokale Lorentzinvarianz bezeichnet haben), sondern um die Tatsache, daß die Gruppe aller Diffeomorphismen der Raumzeit auf sich selbst Eichsymmetrien der Einsteinschen Feldgleichungen sind.
|
Siehe jedoch hier:
http://philsci-archive.pitt.edu/834/1/gr_gauge.pdf
Gravity and Gauge Theory
Steven Weinstein
Perhaps the first thing to note about general relativity is that the diffeomorphism group is not the characteristic group of a group bundle at all. Recall that in a gauge theory, a copy of the gauge group sits over each point of the manifold, and gauge transformations induce changes in the connection (the gauge field) at each point, changes that nonetheless leave the physics at the point unchanged. Diffeomorphisms are a completely different sort of beast — there is no copy of the diffeomorphism group sitting over each point of the manifold, nor is the diffeomorphism group the product G × M of some other internal group G with the manifold M.
Rather than inducing changes in the field at a point, diffeomorphisms map points x to other [other] points x*, and induce changes in the fields (metric tensor, Riemann tensor, etc.) by mapping the fields from one point to another
|
Das ganze Argument scheint mir irgendwie am Thema vorbeizugehen. Der Autor steht anscheinend auf dem Standpunkt, daß Eichgruppen immer vertikal auf irgendeinem Hauptfaserbündel zu wirken haben. Darum geht es hier aber gar nicht. Die Frage ist, ob die Feldgleichungen (oder sogar die Einstein-Hilbert-Wirkung) lokale Symmetrien aufweisen, die zu entsprechenden Noetheridentitäten führen und ob die maximale Symmetriegruppe dieser Gleichungen gerade die Gruppe der Diffeomorphismen ist. Wenn ja, dann bezeichnet man (m.E. nicht nur Physiker) diese Symmetrien traditionell als "Eichsymmetrien". Natürlich haben alle Eichtheorien im Sinne des Autors diese Eigenschaft. Aber das müssen nicht die einzigen sein. Und schließlich geht es nicht darum ob man diese allgemeinere Eigenschaft dann immer noch "Eichsymmetrie" oder irgendwie anders nennt. In jedem Fall wäre es eine nichttriviale Eigenschaft der Feldgleichungen und verdient irgendeinen Namen, z.B. "allgemeine Kovarianz".
Zuletzt bearbeitet von index_razor am 24. Jan 2021 15:24, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 24. Jan 2021 15:21 Titel: TomS Verfasst am: 24. Jan 2021 15:21 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Was du damit meinst, dass “die Observablen normalerweise auch nicht invariant unter Symmetrien der Theorie sind” verstehe ich nicht. |
Die Energie 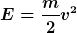 z.B. ist doch keine invariante Funktion unter Galileitransformationen. z.B. ist doch keine invariante Funktion unter Galileitransformationen. |
Das kommt darauf an, wie die Galileitransformationen und Observable definierst.
Mein Lieblingsbeispiel aus der RT ist die Energie eines Objektes mit Viererimpuls p, gemessen von einem Beobachter mit Vierergeschwindigkeit u.
Wenn du sagst,

sei eine Observable, dann ist das nichts anderes als
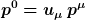
mit
)
also für diesen speziellen Beobachter.
Deswegen kann man auch für festes p
 = u_\mu \, p^\mu )
als Menge von Observablen betrachten, d.h. je Beobachter u eine Observable E.
Nun betrachten wir die Lorentztransformationen
 = (\Lambda u)_\mu \, p^\mu)
 = u_\mu \, (\Lambda p)^\mu)
 = (\Lambda u)_\mu \, (\Lambda p)^\mu = u_\mu \, p^\mu)
Die erste Gleichung definiert eine neue Observable für einen anderen Beobachter jedoch das selbe Objekt; die zweite Gleichung definiert eine neue Observable für den selben Beobachter jedoch für ein anderes Objekt, und die dritte Gleichung definiert i) eine neue Observable für einen anderen Beobachter und ein neues Objekt, sowie ii) die selbe Observable für den selben Beobachter und das selbe Objekt, jedoch in einem anderen Koordinatensystem; üblicherweise ist (ii) gemeint.
Warum sollte das bei Galilei-Transformation nicht genauso funktionieren?
Ich würde deine Idee einfach anders interpretieren; während du sagst, die Observable E sei nicht invariant, sage ich einfach, dass du lediglich eine andere Observable definierst, die dem Rechnung trägt, dass die Energie jetzt von einem anderen Beobachter gemessen wird.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 24. Jan 2021 15:41 Titel: TomS Verfasst am: 24. Jan 2021 15:41 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Unter "passiven" Transformationen verstehe ich einfach Kartenwechsel auf derselben Mannigfaltigkeit M. Eine aktive Transformation ist eine glatte Abbildung  oder auch oder auch  . Letztere sind hier m.E. das nützlichere Konzept, denn "Invarianz unter passiven Transformationen" ist ziemlich bedeutungslos. Potentiell verwirrend ist, daß, wenn man alle Situationen auf M immer durch die Linse einer lokalen Karte betrachtet, der Unterschied zwischen Kartenwechslen auf M und Diffeomorphismen . Letztere sind hier m.E. das nützlichere Konzept, denn "Invarianz unter passiven Transformationen" ist ziemlich bedeutungslos. Potentiell verwirrend ist, daß, wenn man alle Situationen auf M immer durch die Linse einer lokalen Karte betrachtet, der Unterschied zwischen Kartenwechslen auf M und Diffeomorphismen  etwas verschwimmt. etwas verschwimmt.
... Koordinateninvarianz enthält wenig Information, das stimmt. Diffeomorphismeninvarianz der Feldgleichungen enthält Information, wie man daran erkennt, daß nicht alle Gleichungen sie haben. |
Guter Punkt.
Würde das nicht bedeuten, dass man aktive Transformationen auch definieren und Gleichungen bzgl. des Transformationsverhaltens untersuchen kann, ohne überhaupt Karten (Koordinaten) einzuführen?
Dann wäre die Unterscheidung glasklar.
| index_razor hat Folgendes geschrieben: |
Das ganze Argument scheint mir irgendwie am Thema vorbeizugehen. Der Autor steht anscheinend auf dem Standpunkt, daß Eichgruppen immer vertikal auf irgendeinem Hauptfaserbündel zu wirken haben. Darum geht es hier aber gar nicht. Die Frage ist, ob die Feldgleichungen (oder sogar die Einstein-Hilbert-Wirkung) lokale Symmetrien aufweisen, die zu entsprechenden Noetheridentitäten führen und ob die maximale Symmetriegruppe dieser Gleichungen gerade die Gruppe der Diffeomorphismen ist. Wenn ja, dann bezeichnet man (m.E. nicht nur Physiker) diese Symmetrien traditionell als "Eichsymmetrien". |
Mir geht es nicht darum, ob die Bezeichnung “Eichtheorie” dann zutreffend ist oder nicht, sondern wirklich nur darum, dass die “Eichtransformationen auf dem Faserbündel” und die “Diffeomorphismen auf der Mannigfaltigkeit” oder “zwischen Mannigfaltigkeiten” zumindest technisch etwas völlig anderes sind. Und daher kann ich gut damit leben, das eine “Eichtransformationen” und das andere “Diffeomorphismen” zu nennen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Jan 2021 15:42 Titel: index_razor Verfasst am: 24. Jan 2021 15:42 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Was du damit meinst, dass “die Observablen normalerweise auch nicht invariant unter Symmetrien der Theorie sind” verstehe ich nicht. |
Die Energie 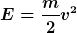 z.B. ist doch keine invariante Funktion unter Galileitransformationen. z.B. ist doch keine invariante Funktion unter Galileitransformationen. |
Das kommt darauf an, wie die Galileitransformationen und Observable definierst.
|
Ich definiere den verallgemeinerten Phasenraum aller Teilchenorte und Geschwindigkeiten und der Zeit. Eine Observable ist eine Funktion auf diesem Raum und eine Galieleitransformation ist die Abbildung

auf diesem Raum. Eine Funktion f ist invariant unter g, wenn (x_i, \dot x_i, t) \stackrel{\text{def}}{=} f(x_i-vt, \dot x_i - v, t) = f(x_i, \dot x_i, t)) . .
Diese Definitionen sind m.E. alle standard in diesem Kontext.
| Zitat: |
Mein Lieblingsbeispiel aus der RT ist die Energie eines Objektes mit Viererimpuls p, gemessen von einem Beobachter mit Vierergeschwindigkeit u.
Wenn du sagst,

sei eine Observable, dann ist das nichts anderes als
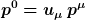
mit
)
also für diesen speziellen Beobachter.
Deswegen kann man auch für festes p
 = u_\mu \, p^\mu )
als Menge von Observablen betrachten, d.h. je Beobachter u eine Observable E.
Nun betrachten wir die Lorentztransformationen
 = (\Lambda u)_\mu \, p^\mu)
 = u_\mu \, (\Lambda p)^\mu)
 = (\Lambda u)_\mu \, (\Lambda p)^\mu = u_\mu \, p^\mu)
Die erste Gleichung definiert eine neue Observable für einen anderen Beobachter jedoch das selbe Objekt; die zweite Gleichung definiert eine neue Observable für den selben Beobachter jedoch für ein anderes Objekt, und die dritte Gleichung definiert i) eine neue Observable für einen anderen Beobachter und ein neues Objekt, sowie ii) die selbe Observable für den selben Beobachter und das selbe Objekt, jedoch in einem anderen Koordinatensystem.
Warum sollte das bei Galilei-Transformation nicht genauso funktionieren?
|
Das funktioniert schon. Allerdings ging es mir ja hier darum "Forminvarianz" als Symmetrie von Gleichungen zu interpretieren. Dieses Symmetriekonzept ist ein rein mathematisches und hat nichts mit irgendwelchen "Beobachtern" zu tun. Aber gut, durch das Wort "Observable" liegt diese Interpretation natürlich auch nicht fern. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Jan 2021 15:54 Titel: index_razor Verfasst am: 24. Jan 2021 15:54 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Unter "passiven" Transformationen verstehe ich einfach Kartenwechsel auf derselben Mannigfaltigkeit M. Eine aktive Transformation ist eine glatte Abbildung  oder auch oder auch  . Letztere sind hier m.E. das nützlichere Konzept, denn "Invarianz unter passiven Transformationen" ist ziemlich bedeutungslos. Potentiell verwirrend ist, daß, wenn man alle Situationen auf M immer durch die Linse einer lokalen Karte betrachtet, der Unterschied zwischen Kartenwechslen auf M und Diffeomorphismen . Letztere sind hier m.E. das nützlichere Konzept, denn "Invarianz unter passiven Transformationen" ist ziemlich bedeutungslos. Potentiell verwirrend ist, daß, wenn man alle Situationen auf M immer durch die Linse einer lokalen Karte betrachtet, der Unterschied zwischen Kartenwechslen auf M und Diffeomorphismen  etwas verschwimmt. etwas verschwimmt.
... Koordinateninvarianz enthält wenig Information, das stimmt. Diffeomorphismeninvarianz der Feldgleichungen enthält Information, wie man daran erkennt, daß nicht alle Gleichungen sie haben. |
Guter Punkt.
Würde das nicht bedeuten, dass man aktive Transformationen auch definieren und Gleichungen bzgl. des Transformationsverhaltens untersuchen kann, ohne überhaupt Karten (Koordinaten) einzuführen?
Dann wäre die Unterscheidung glasklar.
|
Ja, absolut. Wenn ich von Galileiinvarianz, Eichinvarianz oder anderen Symmetrien rede, dann denke ich immer an aktive Transformationen und nicht an Karten/Koordinatensysteme. Alles andere finde ich vollkommen verwirrend.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Das ganze Argument scheint mir irgendwie am Thema vorbeizugehen. Der Autor steht anscheinend auf dem Standpunkt, daß Eichgruppen immer vertikal auf irgendeinem Hauptfaserbündel zu wirken haben. Darum geht es hier aber gar nicht. Die Frage ist, ob die Feldgleichungen (oder sogar die Einstein-Hilbert-Wirkung) lokale Symmetrien aufweisen, die zu entsprechenden Noetheridentitäten führen und ob die maximale Symmetriegruppe dieser Gleichungen gerade die Gruppe der Diffeomorphismen ist. Wenn ja, dann bezeichnet man (m.E. nicht nur Physiker) diese Symmetrien traditionell als "Eichsymmetrien". |
Mir geht es nicht darum, ob die Bezeichnung “Eichtheorie” dann zutreffend ist oder nicht, sondern wirklich nur darum, dass die “Eichtransformationen auf dem Faserbündel” und die “Diffeomorphismen auf der Mannigfaltigkeit” oder “zwischen Mannigfaltigkeiten” zumindest technisch etwas völlig anderes sind.
|
Ja, sie sind etwas anderes. Aber: die Konsequenzen aus diesen "Eichtransformationen auf Faserbündeln", die man aus dem zweiten Noethertheorem ziehen kann, sind hier doch das wichtige. Zu den Folgerungen dieses Theorems gehört z.B., daß die Dynamik des Gravitationsfeldes bestimmten Constraints unterworfen ist. (Genau wie die Dynamik von Eichfeldern.) Es spielt doch dafür physikalisch eine völlig untergeordnete Rolle, ob der Feldtheorie irgendein Hauptfaserbündel zugrundeliegt.
| Zitat: |
Und daher kann ich gut damit leben, das eine “Eichtransformationen” und das andere “Diffeomorphismen” zu nennen. |
Aber "Diffeomorphismen" drückt nicht aus, daß es Noetheridentitäten gibt. "Eichsymmetrie" macht das völlig klar. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 24. Jan 2021 16:20 Titel: TomS Verfasst am: 24. Jan 2021 16:20 Titel: |
 |
|
Ok, ich denke, bzgl. des zweiten Punktes hast du recht, wenn du mit Eichsymmetrie auch die Existenz von Noethertheorem, Constraints etc. verbindest.
Bzgl. der Frage ... “ob das nicht bedeuten würde, dass man aktive Transformationen definiert und Gleichungen bzgl. des Transformationsverhaltens untersucht, ohne überhaupt Karten (Koordinaten) einzuführen” stellt sich mir die Frage, wie das mathematisch funktionieren soll; ich kenne das immer nur über den Umweg der Koordinaten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Jan 2021 18:48 Titel: index_razor Verfasst am: 24. Jan 2021 18:48 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Bzgl. der Frage ... “ob das nicht bedeuten würde, dass man aktive Transformationen definiert und Gleichungen bzgl. des Transformationsverhaltens untersucht, ohne überhaupt Karten (Koordinaten) einzuführen” stellt sich mir die Frage, wie das mathematisch funktionieren soll; ich kenne das immer nur über den Umweg der Koordinaten. |
Vielleicht habe ich deine Frage falsch verstanden. Aber ich meine das Prinzip wird an meiner Definition der Galileitransformation weiter oben deutlich. Mein "verallgemeinerter Phasenraum" besteht aus n Kopien des absoluten Raums  , seines Tangentialraums , seines Tangentialraums 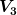 und der Zeit: und der Zeit: 
Auf P kann man im Prinzip definieren was eine Galileitransformation ist ohne Koordinaten einzuführen. Es handelt sich um n Kopien der Abbildung \mapsto x + \vec{v}t) , gefolgt von n Kopien von , gefolgt von n Kopien von  gefolgt von der Identitätsabbildung gefolgt von der Identitätsabbildung  . .
Das kann man natürlich erheblich verallgemeinern um gekrümmte Raumzeiten und Feldtheorien einzubeziehen. Ist es das was du meintest? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 24. Jan 2021 22:38 Titel: TomS Verfasst am: 24. Jan 2021 22:38 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ist es das was du meintest? |
Nee, nicht wirklich. Ich muss selbst noch nachdenken, sorry für die Konfusion meinerseits.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
|
 |
|
|















