| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18123
|
 TomS Verfasst am: 26. Jan 2021 10:02 Titel: Diffeomorphismen und Koordinatentransformationen |
 |
|
So, jetzt bin ich in der Lage, mein Unbehagen besser zu formulieren. Es hängt im wesentlichen damit zusammen, dass Mathematiker und Physiker einen leicht unterschiedlichen Sprachgebrauch pflegen.
Zunächst mal meine Darstellung als Ausgangspunkt:
Koordinatensysteme und -transformationen
Gegeben sei eine Mannigfaltigkeit M mit offenen Umgebungen U_alpha und und Karten chi_alpha, d.h.
Für die nichtleere Schnittmenge zweier Umgebungen
existieren daher zwei Karten
Eine Koordinatentransformation entspricht dann der Abbildung
- eingeschränkt auf diese Schnittmenge.
Diffeomorphismen
Gegeben seien zwei Mannigfaltigkeit M,N sowie eine bijektive, (k-fach) stetig differenzierbare Abbildung f mit ebenfalls (k-fach) stetig differenzierbarer Umkehrabbildung
Vermöge der Karten mit
, \; (V_\beta \subset N, \chi_{N,\beta}) )
kann diese Definition in Koordinaten “übersetzt” werden:
So wie ich die Mathematiker verstanden habe, bleibt es einfach dabei. Damit haben jedoch zeta und phi nichts miteinander zu tun. Andererseits sehe ich nicht, wie ich “stetig differenzierbar” überhaupt koordinatenfrei untersuchen sollte.
Die Physiker identifizieren jetzt M und N und behaupten, ein passiver Diffeomorphismus wäre gerade eine Koordinatentransformation, während ein aktiver einen neue Metrik = eine neue Lösung der Einstein-Gleichungen erzeugen würde.
https://arxiv.org/pdf/gr-qc/9910079.pdf
Loop Quantum Gravity and the Meaning of Diffeomorphism Invariance
Marcus Gaul, Carlo Rovelli
chap. 4, p. 28.
Suppose a given metric is a solution to the Einstein equations, then due to diffeomorphism invariance with
 )
the new metric
 = (\partial_\mu \phi^\rho)(\partial_\nu \phi^\sigma) \, g_{\rho\sigma}(\phi(x)) )
is also a solution.
There are two geometrical interpretations of [this equation] commonly known as passive and active diffeomorphism.
Passive diffeomorphism invariance refers to invariance under change of coordinates, i.e. the same object is represented in different coordinate systems. Choose a (local) coordinate system in which the metric is g. In a second system the metric is given by g-tilde; both of them represent the same metric on M.
Active diffeomorphisms on the other hand relate different objects in M in the same coordinate system. This means that f is viewed as a map associating one point in the manifold to another one. Take for example two points P, Q in M and consider two metrics g and g-tilde which are both solutions of the Einstein equations. Then the distance d between P and Q computed using the two metrics is different, i.e.
} (P,Q) \neq d_{({}^f\!{g})}(P,Q) )
We have two distinct metrics on M which both solve Einstein’s equations. These two metrics might still be related by [the equation mentioned above], i.e. they are related by an active diffeomorphism.
Irgendwie hat er mich da abgehängt.
Rovelli geht dann zu koordinatenfreien Schreibweise über (ich unterscheide zwischen f und phi, Rovelli tut dies nicht; ich habe versucht, die Notation formal korrekt an die obige anzupassen).
 \to d_{(g)}(P,Q) )
}(P,Q) = d\big( f^{-1}(P), f^{-1}(Q) \big))
Meine Probleme sind letztlich folgende.
(*) Was bedeutet es genau, zwei Mannigfaltigkeiten zu “identifizieren”? Wie genau kommt man zur Identifizierung von M und N? Nur dann macht es ja überhaupt Sinn, passive Diffeomorphismen = Koordinatentransformation und aktive Diffeomorphismen gemeinsam zu diskutieren, denn nur dann können die beiden oben eingeführten Umgebungen U in M und V in N überhaupt eine Schnittmenge haben. Auch dann müssen sie doch aber keine Schnittmenge haben, d.h. wenn ich beliebige Diffeomorphismen zulasse, dann kann die Schnittmenge auch leer sein. Das diskutiert aber niemand.
Dann stört mich Rovelli’s “ These two metrics might still be related by [the equation mentioned above], i.e. they are related by an active diffeomorphism.”
Also wenn sie nicht diffeomorph sind, dann sind sie eben verschieden und alles weitere ist irrelevant.
Wenn sie diffeomorph jedoch nicht isometrisch sind, dann sind es für mich im physikalischen Sinne immer noch zwei verschiedene “Raumzeiten” und alles weitere ist wiederum irrelevant.
Wenn sie diffeomorph und sind, dann sind die beiden Raumzeiten für mich im physikalischen Sinne identisch. Dass ich dies abstrakt mittels Diffeomeomorphismen beschreiben kann, ist mir erst mal egal, weil ich doch - sobald ich (*) verstanden habe - dies wieder darauf reduzieren kann, dass eine geeignete Koordinatentransformation vorliegt; und dass Koordinatentransformationen die Physik nicht ändern, ist mir klar.
Ich habe irgendwie den Eindruck, die Physiker führen da ein Scheinproblem ein. Ich verstehe die Beweggründe insoweit, als z.B. im Pfadintegral nicht über diffeomorphe und/oder bzgl. Eichtransformationen äquivalente Konfigurationen summiert werden darf. Also
 \, \delta(f_\text{gauge}))
Das ist zunächst rein formal. Sobald ich aber konkret etwas ausrechnen will, bin ich doch wieder bei Koordinaten. Und da verschwindet der Unterschied zwischen aktiven und passiven Diffeomorphismen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 30. Jan 2021 17:42 Titel: Re: Diffeomorphismen und Koordinatentransformationen |
|
|
| TomS hat Folgendes geschrieben: |
So wie ich die Mathematiker verstanden habe, bleibt es einfach dabei. Damit haben jedoch zeta und phi nichts miteinander zu tun. Andererseits sehe ich nicht, wie ich “stetig differenzierbar” überhaupt koordinatenfrei untersuchen sollte.
|
Das hängt wie immer von der Situation ab und was man über die Abbildung weiß.
Es wird sicher viele Anwendungsfälle geben, in denen der direkteste Weg ist, Differenzierbarkeit bzgl. irgendeiner Karte zu prüfen. Aber der Witz bei der Definition von Mannigfaltigkeiten ist ja gerade, daß es egal ist, welche Karten ich dafür verwende. Deswegen gehört zu jeder Mannigfaltigkeit ja ein maximaler Atlas, dessen Karten alle glatt miteinander wechseln.
| Zitat: |
Die Physiker identifizieren jetzt M und N und behaupten, ein passiver Diffeomorphismus wäre gerade eine Koordinatentransformation, während ein aktiver einen neue Metrik = eine neue Lösung der Einstein-Gleichungen erzeugen würde.
https://arxiv.org/pdf/gr-qc/9910079.pdf
Loop Quantum Gravity and the Meaning of Diffeomorphism Invariance
Marcus Gaul, Carlo Rovelli
chap. 4, p. 28.
[...]
Meine Probleme sind letztlich folgende.
(*) Was bedeutet es genau, zwei Mannigfaltigkeiten zu “identifizieren”? Wie genau kommt man zur Identifizierung von M und N?
|
Normalerweise mittels irgendeines Diffeomorphismus. Aber ich glaube es ist gar nicht nötig, überhaupt zwei verschiedene Mannigfaltigkeiten M und N einzuführen. Gaul und Rovelli reden anscheinend ja auch nur von dem Fall, daß  . Da stellt sich die Frage nach der Identifizierung nicht und dieser Fall läßt sich ja auch am direktesten mit Kartenwechseln auf M vergleichen. Für je zwei Karten  haben wir, falls  , einen lokalen Diffeomorphismus  zwischen zwei Kartengebieten auf M. Und für jede Karte 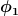 und jeden Diffeomorphismus f (mit geeignet eingeschränktem Definitionsbereich) gibt es eine andere Karte  .
| Zitat: |
Nur dann macht es ja überhaupt Sinn, passive Diffeomorphismen = Koordinatentransformation und aktive Diffeomorphismen gemeinsam zu diskutieren, denn nur dann können die beiden oben eingeführten Umgebungen U in M und V in N überhaupt eine Schnittmenge haben. Auch dann müssen sie doch aber keine Schnittmenge haben, d.h. wenn ich beliebige Diffeomorphismen zulasse, dann kann die Schnittmenge auch leer sein. Das diskutiert aber niemand.
|
Die Definition eines Kartenwechsels bezieht sich auf eine einzige Mannigfaltigkeit und erfordert eine gemeinsame Schnittmenge der Definitionsbereiche. Ein Diffeomorphismus  und eine Karte  definieren zusammen eine weitere Karte auf \subset M) , nämlich }) . Irgendein Kartenwechsel kommt hier nicht vor. Aber die Situation ist für die eigentliche Frage m.E. unnötig kompliziert.
| Zitat: |
Dann stört mich Rovelli’s “ These two metrics might still be related by [the equation mentioned above], i.e. they are related by an active diffeomorphism.”
Also wenn sie nicht diffeomorph sind, dann sind sie eben verschieden und alles weitere ist irrelevant.
Wenn sie diffeomorph jedoch nicht isometrisch sind, dann sind es für mich im physikalischen Sinne immer noch zwei verschiedene “Raumzeiten” und alles weitere ist wiederum irrelevant.
|
Das ist genau der Knackpunkt. Isometrie ist eben nur hinreichend, aber nicht notwendig dafür, daß es sich um physikalisch identische Situationen handelt. Physikalisch kannst du nicht unterscheiden ob du ein Beobachter in der Raumzeit , g)) oder ein Beobachter in der Raumzeit ) bist. Wählst du z.B. eine Karte  in M, sieht alles genauso aus, als hättest du die Karte  in ) gewählt.
Dies Argument läßt die Invarianz wie eine Trivialität erscheinen. Aber ich glaube der eigentliche Punkt hat mit den Einsteingleichungen zu tun und der Tatsache, daß für den Einsteintensor  gilt
Damit haben wir nun eine Differentialgleichung  für g mit einer bestimmten Symmetrieeigenschaft. Dies scheint auf den ersten Blick nur am Tensorcharakter von G zu liegen und daran, daß wir für die Metriktransformation genau den pullback von f verwendet haben.
Aber das ist nicht der Fall. Die Maxwellgleichungen z.B. haben, soweit ich sehe, diese Eigenschaft nicht, obwohl sie ebenfalls ausschließlich aus Tensoren bestehen (und in diesem trivialen Sinne "allgemein kovariant" sind). Das Problem ist die Gleichung mit dem Quellterm
In diese geht der Hodge-Operator und damit die Metrik ein und 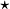 vertauscht nicht mit beliebigen Diffeomorphismen, sondern nur mit orientierungserhaltenden Isometrien. Es gilt also nicht
 = f^\star j \qquad\text{(falsch)})
und damit sind beliebige Diffeomorphismen keine Symmetrien der Maxwellgleichungen und diese nicht allgemein kovariant (jetzt im nichttrivialen Sinne gemeint).
Das bedeutet, denke ich, folgendes: wir können allein mit Hilfe von Gravitationsexperimenten, also z.B. durch Beobachtung neutraler Testteilchen, nicht unterscheiden, ob wir uns in M oder f(M) befinden. Wir können dies aber eventuell durch elektromagnetische Experimente mit Hilfe von geladenen Teilchen tun, deren Verhalten durch die nicht-kovariante Maxwell-Gleichung  beschrieben wird.
| Zitat: |
Wenn sie diffeomorph und [isometrisch?] sind, dann sind die beiden Raumzeiten für mich im physikalischen Sinne identisch. Dass ich dies abstrakt mittels Diffeomeomorphismen beschreiben kann, ist mir erst mal egal, weil ich doch - sobald ich (*) verstanden habe - dies wieder darauf reduzieren kann, dass eine geeignete Koordinatentransformation vorliegt; und dass Koordinatentransformationen die Physik nicht ändern, ist mir klar.
|
Ob ein Diffeomorphismus f lokal bzgl. Karten wie eine Koordinatentransformation aussieht, ist eben nicht der Punkt. Es geht darum ob
 = 0 \Leftrightarrow \text{Diff'gl. für}(g) = 0.)
Bei einem Koordinatenwechsel transformierst du einfach g und was immer dabei aus "Diff'gl" wird, ist eben per Definition dieselbe Gleichung in neuen Koordinaten. Bei einer Symmetrietransformation ist die Frage aber, ob  wieder in der Lösungsmenge von "Diff'gl." liegt. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18123
|
| TomS Verfasst am: 03. Feb 2021 23:59 Titel: |
|
|
Danke für den Beitrag,
Ich hatte hier schon mal eine Antwort stehen, die ich wieder gelöscht hatte, da sie mir letztlich nicht zielführend erschien. Ich bin noch am Denken.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18123
|
| TomS Verfasst am: 07. Feb 2021 15:45 Titel: Re: Diffeomorphismen und Koordinatentransformationen |
|
|
Erst mal danke für deine Hilfe.
Der erste Punkt bzgl. aktiver und passiver Diffeomorphismen ist geklärt; wie so oft ist das trivial, sobald man’s verstanden hat.
Rovelli erklärt den aktiven Diffeomorphismus f
 \in M)
anhand eines Wind-Vektorfeldes V, das eine Temperaturverteilung
 = T(f_V(P)))
über die Erde verschiebt. D.h. die Temperatur bei Q entspricht gerade der früheren Temperatur bei P, die der Wind von P nach Q geblasen hat (ohne Wärmeleitung u.ä., sonst funktioniert das Beispiel nicht).
In Koordinatenschreibweise gilt
 = T\Big( (\chi_\beta \circ f_V \circ \chi_\alpha^{-1})(x_\alpha) \Big) = T\Big( \phi_{\beta,\alpha}(x_\alpha) \Big))
Dies kann andererseits direkt mit einem passiven Diffeomorphismus = einer geeigneten Koordinatentransformation
 = T\Big( (\bar{\chi}_\beta \circ \chi_\alpha^{-1})(x_\alpha) \Big) = T\Big( \zeta_{\beta,\alpha}(x_\alpha) \Big) )
identifiziert werden, ohne dass ein f involviert wäre, d.h. die Temperatur T(Q) kann sowohl als Funktion der Koordinaten x_alpha als auch x_beta aufgefasst werden.
Betrachtet man Vektorfelder als infinitesimale Generatoren von Flüssen (d.h. eindimensionalen Gruppen von Diffeomorphismen) auf M, so ist die Lie-Ableitung das Differential der Darstellung der Diffeomorphismengruppe auf Tensorfeldern. Das Vektorfeld V spielt genau diese Rolle.
Mein Problem war, dass ich immer nach dem physikalischen Unterschied zwischen aktiven und passiven Diffeomorphismen gesucht habe. Ich denke, die simple Lösung ist, dass es keinen gibt ;-)
Der Grund dafür, die lokale Diffeomorphismeninvarianz der Theorie, führt jedoch zu interessanten Schlussfolgerungen bzgl. der Interpretation der Mannigfaltigkeit M, der Punkte P und Q sowie der möglichen Observablen im Rahmen der ART.
Vereinfacht gesagt entspricht eine Raumzeit nicht einer Mannigfaltigkeit M sondern der Äquivalenzklasse
unter Diffeomorphismen.
Die Punkte P und Q haben keine physikalische Bedeutung, T(P) und T(Q) entsprechen keinen Observablen.
Aus dem Beispiel von Rovelli wird das klar. Wenn wir sagen T(“an dem Ort, an dem der Eiffelturm steht; und zu dem Zeitpunkt, zu dem das Richtfest gefeiert wurde”), dann ist das physikalisch definiert. Wenn wir diesen materiellen Gehalt entfernen, so dass eine nackte Mannigfaltigkeit ohne Struktur übrig bleibt, dann ist T(P) ohne physikalischen Gehalt.
Als Nächstes muss ich mir nochmal die Konstruktion einer geeigneten Observablen anschauen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen