| Autor |
Nachricht |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 09. Mai 2020 13:25 Titel: Interpretation der Schrödingergleichung Bernd Stein Verfasst am: 09. Mai 2020 13:25 Titel: Interpretation der Schrödingergleichung |
 |
|
Hallo zusammen,
ich habe eine Frage in die Runde, muss aber etwas ausholen:
Einem Quantenobjekt (Elektron, Lichtquant, o.ä.) kann man im Allgemeinen (von Ausnahmen abgesehen) vor der Messung einer dynamischen Messgroesse keine Eigenschaft der dynamischen Messgroesse zuordnen, weil es keine solche Eigenschaft „besitzt“. Die Frage stellt sich daher, wie soll ich das Quantenobjekt beschreiben, wenn es keine solche Eigenschaften „hat“ ? Wenn ich aus den mathematischen Gleichungen dazu nichts Verbindliches herauslesen kann, welche Grundlage habe ich dann für eine passende Beschreibung ?
Bevor hier zu resignieren, könnte man einen Versuch wie folgt wagen:
Folgendes kann man - ungeachtet jeder Anschaulichkeit – wohl immer sagen:
a) das Quantenobjekt muss (auch wieder von Ausnahmen abgesehen) bei der Propagation durch irgendwelche Räume das bleiben, was es ist. Es muss seine Identität erhalten (Voraussetzung, dass man es beschreiben kann)
b) es muss die Fähigkeit zur Wechselwirkung haben und c) es muss wechselwirken, wenn es einen Wechselwirkungspartner hat (Voraussetzung dafür das es beobachtet werden kann)
Das sind Anforderungen, die normalerweise bei der Betrachtung einer physikalischen Situation vorausgesetzt werden. Wenn ich zum Beispiel sage, das Quantenobjekt hat einen (gemessenen) Ort, dann wurde ja schon vorausgesetzt, dass es als Individuum vor und während der Messung existiert, dass es befähigt ist, eine Wirkung auf ein anderes Objekt (z.B. ein Meßgerät) auszuüben, und dieses am Ort es Meßgerätes auch tut, damit dieses eine Änderung an seinem Ort erfährt, aus der man schließen kann, dass es auch dort war, und dass alles muss reproduzierbar sein, was aus a) verweist.
Insofern erscheinen mir die drei Punkte a)-c) vernünftig, als Grundlage einer Beschreibung zu verwenden:
Punkt a) kennzeichnet nichts anderes als die Tatsache, dass das Objekt beim Propagieren längs einer Trajektorie durch irgendeinen Raum auf beliebig dicht beieinander liegenden Punkten, oder nach dem Durchlaufen beliebig kleiner Abstände, immer wieder „als Gleiches“ vorhanden ist. Das kann man mathematisch so darstellen, dass es in seinem Konfigurationsraum eine Identitätsabbildung gibt, die es sukzessiv immer wieder auf sich selbst abbildet. Im Dreidimensionalen wäre das eine vollständige Drehung D des Objektes q, beginnend mit beliebigem Drehwinkel, und diese Drehung als Operation könnte in der Form Dq=q mit D = exp(it)*exp(ix) (die Zeit t und den Ort x als Drehparameter) dargestellt werden. Im Allgemeinen wäre dies jedoch eine Drehung im physikalischen Konfigurationsraum des Objektes, wir wissen ja nicht, ob sich das Objekt ohne Eigenschaften überhaupt als dreidimensionale Entität auffassen lässt. Aber in diesem Raum müssten mindestens Drehoperationen möglich sein und raumzeitlichen Abständen vergleichbare Abstände existieren, längs derer die obige Identitätsabbildung gilt.
Nun verknüpfe ich dies Identitätsabbildungen mit der Fähigkeit des Objektes, eine Wirkung ausüben zu können. Eine solche Eigenschaft muss das Objekt immer haben, und zwar als notwendige ontische Eigenschaft, damit es überhaupt epistemisch zugänglich ist, und keine physikalische Theorie kann dem Objekt daher diese Eigenschaft vor der Messung absprechen. Wie drückt sich diese Fähigkeit zur Wirkung physikalisch aus? Wirkung ausüben heißt, Wirkungseinheiten längs eines Abstandes im Konfigurationsraum zu übertragen, im Dreidimensonalen längs eines Raumzeitabstandes, also je nach Energie n*h Einheiten h pro Zeitabstand t (E= n*h/t) und je nach Impuls n*h Einheiten pro Raumabstand l (p = n*h/l). Das führt im Dreidimensionalen zur der Identitätsabbildung exp i/h(E*t – p*x), im höherdimensionalen Konfigurationsraum zur entsprechenden Gleichung.
Der Ausdruck exp i/h(E*t – p*x) ist ja nichts weiter als eine Lösung der Schrödingergleichung, wenn diese eine isoliertes Quantenobjekt beschreibt, wobei man üblicherweise davon spricht, das Quantenobjekt würde einer ebenen Welle „entsprechen“, hätte etwas von einer „Materiewelle“ an sich, o.ä.. In Wirklichkeit würde man damit die Lösung aber nur mißinterpretieren. In Wirklichkeit würde die Schrödingergleichung nur aussagen, dass hier ein Quantenobjekt vorhanden ist, das die Fähigkeit, n*h Wirkungseinheiten längs eines raumzeitlichen Abstandes zu übertragen, beginnend an einem beliebigen Punkt der Raumzeit.
Das ist also keine neue Theorie, sondern nur eine andere Interpretation der Gleichung, die davon absieht, irgendwelche Eigenschaften eines Quantenobjektes (z.B. Welleneigenschaften) aus dem mathematischen Formalismus herauszulesen, sondern nur auf die einzige Eigenschaft abstellt, die jedes physikalische Objekt immer hat, nämlich die Fähigkeit zu einer Wirkung, auf ein anderes Objekt, sofern dieses in der Nähe. Ist kein anderes in der Nähe, hat es einfach nur diese Eigenschaft, und darüber hinaus macht die Theorie keine Aussage
Nach dieser langen Vorrede: habt ihr Einwände gegen diese Interpretation- oder anders gefragt, steht diese Beschreibung im Widerspruch zu physikalischen Erkenntnissen oder zu zwingenden Schlussfolgerungen aus der Mathematik ? Und welche weiteren Schlussfolgerungen könnte man aus der Sicht des Physikers daraus ziehen ?
Über einen Kommentar dazu würde ich mich sehr freuen.
Grüße
Bernd Stein |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Mai 2020 14:21 Titel: Re: Interpretation der Schrädingergleichung index_razor Verfasst am: 09. Mai 2020 14:21 Titel: Re: Interpretation der Schrädingergleichung |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Hallo zusammen,
ich habe eine Frage in die Runde, muss aber etwas ausholen:
Einem Quantenobjekt (Elektron, Lichtquant, o.ä.) kann man im Allgemeinen (von Ausnahmen abgesehen) vor der Messung einer dynamischen Messgroesse keine Eigenschaft der dynamischen Messgroesse zuordnen, weil es keine solche Eigenschaft „besitzt“.
|
Doch, eine dynamische Größe G besitzt im Zustand 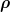 eine Reihe von Eigenschaften völlig unabhängig von jeglicher Messung, z.B. den Erwartungswert eine Reihe von Eigenschaften völlig unabhängig von jeglicher Messung, z.B. den Erwartungswert ) , die Unschärfe , die Unschärfe  - \langle G \rangle^2}) usw. usw.
Die Schwierigkeiten, von denen man in diesem Zusammenhang immer hört und über die es sogar eine Menge Theoreme gibt, basieren auf der Annahme, daß alle objektiven Eigenschaften eines Quantensystems Eigenwerte einer zugehörigen Observable sein müssen. Der einzige Grund für diese Annahme ist die Bornsche Regel, die diese Eigenwerte mit "Messergebnissen" in Beziehung setzt. Da für den Begriff "Messung" keine präzise Definition existiert, ist aber auch die Bedeutung dieser Theoreme unklar. Es sind insbesondere auch keineswegs alle physikalisch meßbaren Größen Eigenwerte irgendwelcher Operatoren.
| Zitat: |
Die Frage stellt sich daher, wie soll ich das Quantenobjekt beschreiben, wenn es keine solche Eigenschaften „hat“ ? Wenn ich aus den mathematischen Gleichungen dazu nichts Verbindliches herauslesen kann, welche Grundlage habe ich dann für eine passende Beschreibung ?
|
Du gehst von falschen Voraussetzungen aus. Aus den mathematischen Gleichungen der Quantentheorie kannst du sehr viel Verbindliches herauslesen.
| Zitat: |
Punkt a) kennzeichnet nichts anderes als die Tatsache, dass das Objekt beim Propagieren längs einer Trajektorie durch irgendeinen Raum auf beliebig dicht beieinander liegenden Punkten, oder nach dem Durchlaufen beliebig kleiner Abstände, immer wieder „als Gleiches“ vorhanden ist.
|
Das klingt so, als versuchtest du einfach die Zeitentwicklung eines physikalischen Systems zu beschreiben. Die korrekte mathematische Formulierung dafür ist mittels eines Flusses (oder etwas sehr ähnlichem). Dies müssen nicht unbedingt Drehungen sein, wie du im folgenden behauptest, und sind es natürlich auch im allgemeinen nicht.
| Zitat: |
Das kann man mathematisch so darstellen, dass es in seinem Konfigurationsraum eine Identitätsabbildung gibt, die es sukzessiv immer wieder auf sich selbst abbildet. Im Dreidimensionalen wäre das eine vollständige Drehung D des Objektes q, beginnend mit beliebigem Drehwinkel, und diese Drehung als Operation könnte in der Form Dq=q mit D = exp(it)*exp(ix) (die Zeit t und den Ort x als Drehparameter) dargestellt werden.
|
Das klingt nicht gerade einleuchtend. Was soll "exp(ix)" mit einem dreidimensionalen Ort x überhaupt bedeuten? In welcher Ebene wird hier gedreht und wieso redest du überhaupt von Drehungen? Und wäre eine "vollständige Drehung" im Dreidimensionalen nicht ohnehin noch einfacher durch D=1 zu beschreiben?
Der Rest dieser Ableitung ergibt für mich leider ebensowenig Sinn. Hier nur ein Punkt, über den du vielleicht noch nachdenken könntest: Würdest du nicht sagen, daß deine Voraussetzungen a) bis c) ebenso für "klassische Objekte" in der klassischen Mechanik zutreffen? Kann es also plausibel sein, daß aus ihnen allein eine Lösung der Schrödingergleichung folgt? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 09. Mai 2020 17:35 Titel: Re: Interpretation der Schrödingergleichung TomS Verfasst am: 09. Mai 2020 17:35 Titel: Re: Interpretation der Schrödingergleichung |
 |
|
| Bernd Stein hat Folgendes geschrieben: | | Einem Quantenobjekt kann man im Allgemeinen vor der Messung einer dynamischen Messgroesse keine Eigenschaft der dynamischen Messgroesse zuordnen, weil es keine solche Eigenschaft „besitzt“. Die Frage stellt sich daher, wie soll ich das Quantenobjekt beschreiben, wenn es keine solche Eigenschaften „hat“ ? Wenn ich aus den mathematischen Gleichungen dazu nichts Verbindliches herauslesen kann, welche Grundlage habe ich dann für eine passende Beschreibung ? |
Zunächst mal hast du die Gleichungen, insbs. die Schrödingergleichung.
Alles, was in den Gleichungen drinsteckt und sich entsprechend dieser dynamisch entwickelt, darfst du dem Objekt zuschreiben.
Dabei handelt es sich nicht um die von dir erwarteten klassischen Eigenschaften oder Messgrößen, aber das ist das Problem deiner Erwartungshaltung und dem zumeist nicht ausreichend definierten Begriff der Messung.
| Bernd Stein hat Folgendes geschrieben: | | a) das Quantenobjekt muss bei der Propagation das bleiben, was es ist. Es muss seine Identität erhalten. |
Das mag im Rahmen der Quantenmechanik von Einteilchensystemen naheliegend erscheinen, ist es aber im Kontext von Vielteilchensystemen oder der relativistischen Quantenfeldtheorie sicher nicht: Photonen und andere effektive oder Quasiteilchen, instabile Atomkerne oder Elementarteilchen, oszillierende Neutrinos, Quarks im Nukleon.
| Bernd Stein hat Folgendes geschrieben: | | b) es muss die Fähigkeit zur Wechselwirkung haben und c) es muss wechselwirken, wenn es einen Wechselwirkungspartner hat (Voraussetzung dafür das es beobachtet werden kann) |
Offenbar muss ein Quantenobjekt mit einem größeren Quantensystem - dem Messgerät - wechselwirken können, jedoch folgt die Beschreibung der Messung gerade nicht der üblichen Dynamik gemäß der Schrödingergleichung inklusive der aus ihr folgenden Wechselwirkung.
Dieser Ansatz ist aufgrund des Messproblems kein günstigeren Ausgangspunkt.
| Bernd Stein hat Folgendes geschrieben: | | Wenn ich zum Beispiel sage, das Quantenobjekt hat einen (gemessenen) Ort, dann wurde ja schon vorausgesetzt, dass es als Individuum vor und während der Messung existiert ... |
Das trifft z.B. auf ein Photon nicht zu. Mir fällt kaum eine Messung irgendeiner Eigenschaft eines Photons ein, bei der das Photon nicht zerstört würde.
| Bernd Stein hat Folgendes geschrieben: | | Punkt a) kennzeichnet nichts anderes als die Tatsache, dass das Objekt beim Propagieren längs einer Trajektorie durch irgendeinen Raum auf beliebig dicht beieinander liegenden Punkten, oder nach dem Durchlaufen beliebig kleiner Abstände, immer wieder „als Gleiches“ vorhanden ist. |
Was meinst du mit “Trajektorie”?
Ganz allgemein mag das für einen Zustandsvektor im Hilbertraum gelten. Ansonsten kenne ich keine Trajektorie im Rahmen der Quantenmechanik.
Und wie oben gesagt bleibt das Objekt zumindest im herkömmlichen Sinne im Allgemeinen nicht “das Gleiche”.
| Bernd Stein hat Folgendes geschrieben: | | Nach dieser langen Vorrede: habt ihr Einwände gegen diese Interpretation- oder anders gefragt, steht diese Beschreibung im Widerspruch zu physikalischen Erkenntnissen ... |
s.o.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 09. Mai 2020 18:21 Titel: Bernd Stein Verfasst am: 09. Mai 2020 18:21 Titel: |
 |
|
Hi Indey Razor,
danke für Deinen Kommentar, den ich allerdings nicht so ganz verstehe. Was soll der „Erwartungswert“ oder die „Unschärfe“ für eine Eigenschaft sein ? Der Erwartungswert ist, soviel ich weiß, eine reelle Zahl ohne physikalische Einheit, und kann doch schon deshalb keine physikalische Eigenschaft sein. Unschärfe kennzeichnet eine Streuung, was soll das für eine Eigenschaft sein ? Es geht mir im übrigen wie beschrieben um dynamische physikalische Eigenschaften (relationale Eigenschaften), die das Quantenobjekt nicht „hat“, also keine intrinsichen, wobei ich jetzt mal die philosophischen Implikationen des „Eigenschaft Habens“ bei einer nicht-intrinsichen Eigenschaft nicht unbedingt diskutieren will. Es geht eigentlich nur um die Tatsache, dass man einfach nicht sagen kann, ein Quantenobjekt hat die oder die dynamischen Eigenschaften, wie Ort, oder Energie oder Impuls (solange es nicht in einem Eigenzustand ist) – es fehlt einfach an Grundlagen für diese Aussage.
Offenbar bist Du der Meinung, diese Grundlage gäbe es, aber sage doch dann, was Verbindliches Du aus der Schrödingergleichung oder aus dem mathematischen Apparat für eine solche Beschreibung herauslesen kannst.
Ich versuche, die Beschreibung des Quantenobjektes auf eine sichere Grundlage zu stellen. Ich kann nicht sagen, ob da irgendwie ein „Fluss“ ist oder etwas „Ähnliches“ – zumal ein solche Beschreibung viel zu wenig konkret wäre, um damit etwas anzufangen - was für ein Medium soll da fließen ? Solche voraussetzungsvollen Konzepte sind nach meiner Ansicht gar nicht nötig. Es reicht einfach zu sagen, da ist etwas, und das bleibt was es ist. Das reicht. Schon darauf kann ich eine Beschreibung mittels Identitätsabbildungen aufbauen.
„Wieso redest du überhaupt von Drehungen?“ Nun ja, soweit ich dies überblicke, ist die vollständige Drehung die einzige Symmetrieoperation, die ein Objekt oder System über eine Operation wieder in sich selbst überführt. Es geschieht etwas, ohne dass sich was ändert – das ist genau das, worauf man aufbauen kann, wenn man ein Objekt, welches einer Dynamik unterworfen ist, beschreiben will, welches aber keine dynamischen physikalischen Eigenschaften „hat“ (im Sinne von Verknüpfung nicht möglich), die man bei der Beschreibung verwenden könnte. Drehungen sind ja Elemente der Drehgruppe, deren Elemente in der SU(2) durch exp(i φ) dargestellt werden. Ob der Drehparameter nun φ oder t oder x heißt, spielt keine Rolle, es kommt hier nur darauf an, dass in dem Raum , in dem sich das Objekt befindet, eine Drehoperation (=Indentitätsoperation) möglich ist. Wenn ja kann sie so mathematisch als Element der Drehgruppe definiert und dargestellt werden.
Ich benötige für die Beschreibung keinen Fluss, oder irgendwelche Dichten oder Wellen im Raum oder sonst irgendwelche Metaphern, die eh nur zu Missverständnissen führen. Ich behaupte nur, wenn ich das Objekt längs einer Trajektorie korrekt beschreiben will, dann kann ich nur sagen, es bleibt längs dieser Trajektorie immer das Gleiche, und die zugehörige mathematische Beschreibung besteht aus der mathematischen Darstellung sukzessiv durchgeführter Drehungen (oder Identitätsabbildungen des Objektes auf sich selbst).
Soweit zu den Grundlagen meiner Überlegungen.
Natürlich gilt das auch für klassische Objekte. Der Unterschied zwischen Quantenobjekten und klassischen Objekten besteht ja nur darin, dass ich klassischen Objekten immer reelle Werte für deren dynamische physikalische Eigenschaften zuweisen kann, Quantenobjekten nicht. Ich brauche also Identitätsabbildungen längs der Trajektorie zur Beschreibung nicht, weil die Identität des Objektes durch die Permanenz der zugewiesenen Eigenschaften gewährleistet ist.
Wodurch kann ich diese Identität bei einem Quantenobjekt gewährleisten ? Ich habe keine reellen Werte für irgendwelche Eigenschaften, die gleichbleibend dem Objekt anhaften und ihm eine permanente Identität geben. Das müssen die Identitätsoperationen leisten, es ist nichts anderes da.
Was spricht aus physikalischer Sicht dagegen?
Grüße
Bernd |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Mai 2020 18:29 Titel: Re: Interpretation der Schrödingergleichung index_razor Verfasst am: 09. Mai 2020 18:29 Titel: Re: Interpretation der Schrödingergleichung |
 |
|
| TomS hat Folgendes geschrieben: |
| Bernd Stein hat Folgendes geschrieben: | | a) das Quantenobjekt muss bei der Propagation das bleiben, was es ist. Es muss seine Identität erhalten. |
Das mag im Rahmen der Quantenmechanik von Einteilchensystemen naheliegend erscheinen, ist es aber im Kontext von Vielteilchensystemen oder der relativistischen Quantenfeldtheorie sicher nicht: Photonen und andere effektive oder Quasiteilchen, instabile Atomkerne oder Elementarteilchen, oszillierende Neutrinos, Quarks im Nukleon.
|
"Das Quantenobjekt" kann eben keine feste Anzahl von "Teilchen" sein. Das ist aber auch schon alles. Quantenfelder bzw. deren n-Punktfunktionen bleiben aber während ihrer Propagation durchaus "was sie sind" und beschreiben die Dynamik der von dir aufgezählten Quantensysteme vollständig.
| Zitat: |
| Bernd Stein hat Folgendes geschrieben: | | Punkt a) kennzeichnet nichts anderes als die Tatsache, dass das Objekt beim Propagieren längs einer Trajektorie durch irgendeinen Raum auf beliebig dicht beieinander liegenden Punkten, oder nach dem Durchlaufen beliebig kleiner Abstände, immer wieder „als Gleiches“ vorhanden ist. |
Was meinst du mit “Trajektorie”?
Ganz allgemein mag das für einen Zustandsvektor im Hilbertraum gelten. Ansonsten kenne ich keine Trajektorie im Rahmen der Quantenmechanik.
|
Das Ehrenfestsche Theorem liefert im Prinzip eine Menge solcher Trajektorien. In der 1-Teilchen QM u.a. auch eine im dreidimensionalen Raum. Ich bezweifle zwar das Bernd Stein dieses Theorem im Sinn hatte, halte es aber für möglich, daß seine Aussagen in bezug auf diese Trajektorien einen gewissen Sinn haben können. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 09. Mai 2020 18:41 Titel: Re: Interpretation der Schrödingergleichung TomS Verfasst am: 09. Mai 2020 18:41 Titel: Re: Interpretation der Schrödingergleichung |
 |
|
| index_razor hat Folgendes geschrieben: | | "Das Quantenobjekt" kann eben keine feste Anzahl von "Teilchen" sein. Das ist aber auch schon alles. Quantenfelder bzw. deren n-Punktfunktionen bleiben aber während ihrer Propagation durchaus "was sie sind" und beschreiben die Dynamik der von dir aufgezählten Quantensysteme vollständig. |
Ja.
Aber hatte der Fragesteller das im Sinn?
| index_razor hat Folgendes geschrieben: | | Das Ehrenfestsche Theorem liefert im Prinzip eine Menge solcher Trajektorien. In der 1-Teilchen QM u.a. auch eine im dreidimensionalen Raum. Ich bezweifle zwar das Bernd Stein dieses Theorem im Sinn hatte ... |
Ich bezweifle das auch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 09. Mai 2020 18:48 Titel: Bernd Stein Verfasst am: 09. Mai 2020 18:48 Titel: |
 |
|
Hi Tom,
ich suche nach Grundlagen für eine Beschreibung, nicht nach einer Beschreibung, die alle Eventualitäten abdeckt, wie das Vergehen und Entstehen von Teilchen, oder eine Beschreibung für die Wechselwirkung des Objektes mit einem Messgerät, oder gar irgendeine neue Theorie.
Mein Motiv ist, dass aus der Schrödingergleichung nicht herausgelesen werden kann, wie ein Quantenobjekt zu beschreiben ist. Die Lösungen zum Beispiel für ein freies Teilchen sind formal ebene Wellen – was soll ich an diesen Lösungen ablesen ? Das Teilchen sich wie Wellen verhalten ? Muss ich sowas verstehen müssen ? Ich denke nicht, dass das irgendjemand versteht.
Wenn die Lösungen ebene Wellen sind, könnte dies doch einen ganz anderen Grund haben. Es könnte doch sein, dass die Schrödingergleichung nur sagt (nicht mehr und nicht weniger): ein Quantenobjekt bleibt immer das Gleiche, solange es frei (isoliert) ist, und dieses Gleichbleiben ist dadurch garantiert, dass es sich bei seiner Propagation durch den Raum, in dem es sich befindet, immer wieder auf sich selbst abbildet, dies ausgedrückt in Form eines mathematischen Ausdrucks, der einer ebene Welle gleichkommt.
Es ist nur eine andere Interpretation der Lösung.
Bitte bedenke auch, dass ich eine fundamentale Eigenschaft jedem physikalischen Objekt zubilligen muss, nämlich die Fähigkeit zu einer (lokalen) Wechselwirkung – im Sinne einer intrinsischen Eigenschaft, sonst würde ein solches Objekt niemals physikalisch in Erscheinung treten. Das ist also keine „schlechte Voraussetzung“, sondern die Voraussetzung, dass in unserer Welt überhaupt etwas Gegenständliches existiert und wahrgenommen werden kann.
Grüße
Bernd |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Mai 2020 19:26 Titel: index_razor Verfasst am: 09. Mai 2020 19:26 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Hi Indey Razor,
danke für Deinen Kommentar, den ich allerdings nicht so ganz verstehe. Was soll der „Erwartungswert“ oder die „Unschärfe“ für eine Eigenschaft sein ? Der Erwartungswert ist, soviel ich weiß, eine reelle Zahl ohne physikalische Einheit, und kann doch schon deshalb keine physikalische Eigenschaft sein. Unschärfe kennzeichnet eine Streuung, was soll das für eine Eigenschaft sein ? |
Der "Erwartungswert" des Impulses hat natürlich auch die Einheit des Impulses, also z.B kg m/s. Dasselbe gilt für die Impuslunschärfe. Daß diese Größen alle eine statistische Konnotation haben, liegt nur daran, daß die Terminologie der Quantenmechanik historisch ziemlich eng mit der Bornschen Regel verknüpft ist, die von "Übergangswahrscheinlichkeiten" spricht. In der modernen Formulierung spricht sie sogar nur noch von Wahrscheinlichkeiten für Meßergebnisse, was keine günstige Grundlage ist.
Wenn man sich nicht von vornherein auf eine statistische Interpretation festlegen will, kann man einfach die quantenmechanischen "Erwartungswerte" mit den zugehörigen physikalische Größen identifizieren. Diese folgen bis auf "Quantenkorrekturen", die durch die Unschärfen abgeschätzt werden können, den klassischen Gleichungen. Die Frage, was der "Impulserwartungswert" für eine Eigenschaft sein soll bekommt also genau dieselbe Antwort wie die Frage was der Impuls für eine Eigenschaft sein soll.
Die Unschärfen selbst sind rein quantenmechanische Größen ohne klassische Entsprechung. Man kann sie sich vorstellen als intrinsische Unsicherheiten der zugehörigen Größe. So wie z.B. der "Ort" eines nicht punktförmigen Objekts eine intrinsische Unsicherheit besitzt, die nichts mit Statistik zu tun hat.
| Zitat: | Es geht eigentlich nur um die Tatsache, dass man einfach nicht sagen kann, ein Quantenobjekt hat die oder die dynamischen Eigenschaften, wie Ort, oder Energie oder Impuls (solange es nicht in einem Eigenzustand ist) – es fehlt einfach an Grundlagen für diese Aussage.
|
Doch, das sage ich ja. Man darf nur nicht voraussetzen, wie du es hier wieder tust, daß alle objektiven Eigenschaften Eigenwerte sein müssen und folglich nur Eigenzustände sie haben können. Wenn man dies nicht voraussetzt, ist es kein Problem davon zu sprechen, daß ein Quantensystem alle diese Eigenschaften (und noch mehr) hat.
| Zitat: |
Offenbar bist Du der Meinung, diese Grundlage gäbe es, aber sage doch dann, was Verbindliches Du aus der Schrödingergleichung oder aus dem mathematischen Apparat für eine solche Beschreibung herauslesen kannst.
|
Das habe ich doch: Die Größen , \text{Tr}(\rho G^2), ...) , deren Dynamik und alles was daraus ableitbar ist, bilden für mich eine solche Grundlage. , deren Dynamik und alles was daraus ableitbar ist, bilden für mich eine solche Grundlage.
| Zitat: |
Ich versuche, die Beschreibung des Quantenobjektes auf eine sichere Grundlage zu stellen. Ich kann nicht sagen, ob da irgendwie ein „Fluss“ ist oder etwas „Ähnliches“ – zumal ein solche Beschreibung viel zu wenig konkret wäre, um damit etwas anzufangen - was für ein Medium soll da fließen ?
|
Dir ist schon klar, daß "Fluß" ein mathematischer Fachbegriff ist? Genauso könntest du fragen, was an einem Ring rund ist. Unkonkret ist daran selbstverständlich auch nichts. Es ist einfach ein allgemeiner Begriff, mit dem man alle möglichen Dynamiken beschreiben kann.
| Zitat: |
Solche voraussetzungsvollen Konzepte sind nach meiner Ansicht gar nicht nötig. Es reicht einfach zu sagen, da ist etwas, und das bleibt was es ist. Das reicht.
|
Um eine Lösung der Schrödingergleichung abzuleiten, reicht es nicht.
| Zitat: |
„Wieso redest du überhaupt von Drehungen?“ Nun ja, soweit ich dies überblicke, ist die vollständige Drehung die einzige Symmetrieoperation, die ein Objekt oder System über eine Operation wieder in sich selbst überführt.
|
Nein, das hängt vom Objekt ab. Und eine "vollständige Drehung" ist im dreidimensionalen Raum eine triviale Operation. Sie ist genau dasselbe wie ein Verschiebung um die Entfernung null. Darauf kann man gar nichts aufbauen.
| Zitat: |
Es geschieht etwas, ohne dass sich was ändert – das ist genau das, worauf man aufbauen kann, wenn man ein Objekt, welches einer Dynamik unterworfen ist, beschreiben will, welches aber keine dynamischen physikalischen Eigenschaften „hat“ (im Sinne von Verknüpfung nicht möglich), die man bei der Beschreibung verwenden könnte. Drehungen sind ja Elemente der Drehgruppe, deren Elemente in der SU(2) durch exp(i φ) dargestellt werden. Ob der Drehparameter nun φ oder t oder x heißt, spielt keine Rolle, es kommt hier nur darauf an, dass in dem Raum , in dem sich das Objekt befindet, eine Drehoperation (=Indentitätsoperation) möglich ist.
|
Der "Drehparameter" ist eine Zahl. Der Ort x ist keine Zahl. Mit Ausnahme der Binsenweisheiten, die du einstreust, wie "Drehungen sind Elemente der Drehgruppe", ergibt das alles keinen Sinn.
| Zitat: |
Wenn ja kann sie so mathematisch als Element der Drehgruppe definiert und dargestellt werden.
|
Die triviale Operation, die du beschreibst, kannst du als Element jeder Gruppe darstellen.
| Zitat: |
Ich benötige für die Beschreibung keinen Fluss, oder irgendwelche Dichten oder Wellen im Raum oder sonst irgendwelche Metaphern, die eh nur zu Missverständnissen führen.
|
Das Wort "Fluß" aus meinem letzten Beitrag war ein Link zu einem Wikipediaartikel, der den Begriff genau definiert. Darin kannst du dich etwas schlauer machen.
| Zitat: |
Ich behaupte nur, wenn ich das Objekt längs einer Trajektorie korrekt beschreiben will, dann kann ich nur sagen, es bleibt längs dieser Trajektorie immer das Gleiche, und die zugehörige mathematische Beschreibung besteht aus der mathematischen Darstellung sukzessiv durchgeführter Drehungen (oder Identitätsabbildungen des Objektes auf sich selbst).
|
Auch das ergibt keinen Sinn. Entlang einer Trajektorie ändert sich normalerweise irgendwas. Unter der Identitätsabbildung ändert sich gar nichts.
| Zitat: |
Soweit zu den Grundlagen meiner Überlegungen.
Natürlich gilt das auch für klassische Objekte. Der Unterschied zwischen Quantenobjekten und klassischen Objekten besteht ja nur darin, dass ich klassischen Objekten immer reelle Werte für deren dynamische physikalische Eigenschaften zuweisen kann, Quantenobjekten nicht.
|
Doch, für hermitesche Operatoren G ist ) eine reelle Zahl, die man dem System im Zustand eine reelle Zahl, die man dem System im Zustand 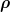 zuordnen kann. Wie gesagt, du gehst von falschen Voraussetzungen aus. zuordnen kann. Wie gesagt, du gehst von falschen Voraussetzungen aus. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Mai 2020 19:41 Titel: Re: Interpretation der Schrödingergleichung index_razor Verfasst am: 09. Mai 2020 19:41 Titel: Re: Interpretation der Schrödingergleichung |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | "Das Quantenobjekt" kann eben keine feste Anzahl von "Teilchen" sein. Das ist aber auch schon alles. Quantenfelder bzw. deren n-Punktfunktionen bleiben aber während ihrer Propagation durchaus "was sie sind" und beschreiben die Dynamik der von dir aufgezählten Quantensysteme vollständig. |
Ja.
Aber hatte der Fragesteller das im Sinn?
|
Nein, offensichtlich sind seine Vorstellungen ja sehr vage. Mich interessiert daher, was genau man im Sinn haben müßte, damit seine Behauptungen nicht mehr offensichtlich der Quantenmechanik widersprechen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Das Ehrenfestsche Theorem liefert im Prinzip eine Menge solcher Trajektorien. In der 1-Teilchen QM u.a. auch eine im dreidimensionalen Raum. Ich bezweifle zwar das Bernd Stein dieses Theorem im Sinn hatte ... |
Ich bezweifle das auch. |
Das ist aber trotzdem kein Grund für dich, außer der des Zustandsvektors, im Rahmen der Quantenmechanik keine weiteren Trajektorien zu kennen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 09. Mai 2020 21:19 Titel: Re: Interpretation der Schrödingergleichung TomS Verfasst am: 09. Mai 2020 21:19 Titel: Re: Interpretation der Schrödingergleichung |
 |
|
| index_razor hat Folgendes geschrieben: | | Das ist aber trotzdem kein Grund für dich, außer der des Zustandsvektors, im Rahmen der Quantenmechanik keine weiteren Trajektorien zu kennen. |
Du hast recht, in dieser Form sind weitere Größen ableitbar, für die dann Trajektorien vorliegen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 09. Mai 2020 23:05 Titel: Bernd Stein Verfasst am: 09. Mai 2020 23:05 Titel: |
 |
|
Hi index razor,
Dass der "Erwartungswert" des Impulses natürlich auch die Einheit des Impulses, also z.B kg m/s hat, höre ich zum ersten Mal. Warum schreibst Du "Erwartungswert" in Anführungszeichen - welcher Erwartungswert ist damit gemeint ? Ich kenne Erwartungswerte nur als dimensionslose Zahlen zwischen Null und Eins. Dass man aus dem mathematischen Formalismus der Quantenmechanik alles mögliche herausdeuten kann, ist mir bekannt, und meinetwegen mag man da herausdeuten, dass man Quantenobjekten vor der Messung einen "Erwartungswert" für einen Energiewert oder einen Impuls, also Werte für diese Eigenschaften in einer ontologischen Schwankungsbreite, zuordnen kann. Aber das widerspricht ja meiner Behauptung nicht, dass das Objekt vor der Messung keine physikalischen Eigenschaften hat, mit denen es zu einem Objekt mit persistierenden Eigenschaften würde, die es identifizierbar machen. Es ist ja hinsichtlich seiner Eigenschaften dann immer noch unscharf.
Ich denke mal, da wirst der These zustimmen, dass - wenn die Schrödingergleichung überhaupt irgend was beschreibt - dass sie dann das beschreibt, womit man ein Quantenobjekt vor der Messung identifizieren kann (was seine Identität "ausmacht"). Sie würde ja sonst - ja was ? - beschreiben ? Es gibt dann zwei Aspekte, und zwar der Aspekt der ontischen Eigenschaften des Objekts und der der (spezifischen) Wirkung des Objekts. Beide können operativ der Identifizierung dienen (müssen nicht unbedingt kategorial verschieden sein). Im Fall eines freien Teilchens gibt es aber keine Wirkung, daher können nur Eigenschaften operativ zur Identifikation dienen.
Folglich muss die Schrödingergleichung für ein freies Quantenobjekt die das Objekt identifizierenden Eigenschaften beschreiben. Wir müßten darüber erst mal Einigkeit herstellen. Wenn Du meinst, das sei nicht der Fall, dann müßtest Du sagen, was sie anderweitig beschreibt. Mit beschreiben meine ich, dass sie d a r ü b e r etwas verschlüsselt aussagt - aber eben auch nicht mehr. Und das man das entschlüsseln muss.
Es stellen sich doch zwei Fragen: Welche Eigenschaften sind das ? Und wie macht sie das, oder anders gesagt, wie entschlüsselt man das ? Und ich behaupte nun, die einzige Eigenschaft, der man sich sicher sein kann, dass das Quantenobjekt diese immer hat, und über die die Schrödingergleichung uns etwas sagen m u s s , ist die Fähigkeit zu einer Wirkung. Das heißt nicht, dass ein Quantenobjekt immer eine Wirkung ausübt - das eben nicht - sondern nur, dass es diese Fähigkeit hat. Das drückt sich zum Beispiel (unabh. von der Schrödingergleichung) aus in der Gleichung E = h*v, dass nämlich ein Strahlungsfeld mit der Energie E nur n*h Wirkungseinheiten pro Zeiteinheit (bei n Schwingungen pro Zeiteinheit) übertragen kann. Es muss diese Wirkung nicht übertragen, wenn es sich ausbreitet, es kann diese übertragen, es ist eine Fähigkeit, die dem Stahlungsfeld innewohnt, eine Potenz. Diese Potenz zur Wirkung hat jedes Quantenobjekt. Falls Du hier Zweifel hast, wäre es gut, Du würdest das sagen. Man kann sich seiner Sache ja nie sicher sein.
Wenn also die Fähigkeit zu einer Wirkung dem Quantenobjekt notwendigerweise innewohnt, als gleichbleibendes Identifikationsmerkmal, w i e beschreibt die Schrödingergleichung das ? Wie kann ich das aus ihr direkt oder aus ihren Lösungen herauslesen, wenn sie ein Objekt beschreibt, das diese Potenz einfach nur hat, und diese Potenz überhaupt nicht realisiert. Das was das Objekt zu einem Individuum macht, ist doch zweierlei, einmal das es diese Potenz hat, und dass es diese permanent hat. Beides muss in der Schrödingergleichung oder in ihren Lösungen abgebildet sein. Ich behaupte nun, dass es dadurch abgebildet ist, dass die ebene Welle als Lösung Identitätsoperationen darstellen, mit E/h*t und p/h*x als Parameter (im Dreidimensionalen, weil hier der Konfigurationsraum der 3-dim. Raum entspricht, mit t als Zeitparameter).
Bitte sage mir, wenn dies physikalischen Erkenntnissen widerspricht, was das genau ist - nicht, dass man die Schrödingergleichung und ihre Lösung für ein freies Teilchen auch anders interpretieren kann, oder dass dies gängigerweise so gemacht wird - sondern welche Erkenntnis diese - von mir in den Raum gestellte These - These h i n f ä l l i g macht.
Ich will mich nicht festbeißen, man muss ja kritisch bleiben. Aber Deine Einwände treffen bisher irgendwie nicht den Punkt. Ich bemüh mich, nachzuvollziehen, was Du dagegen schreibst, aber kriege das nicht wirklich hin.
Grüße
Bernd |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Mai 2020 09:26 Titel: index_razor Verfasst am: 10. Mai 2020 09:26 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: |
Dass der "Erwartungswert" des Impulses natürlich auch die Einheit des Impulses, also z.B kg m/s hat, höre ich zum ersten Mal. Warum schreibst Du "Erwartungswert" in Anführungszeichen - welcher Erwartungswert ist damit gemeint ? Ich kenne Erwartungswerte nur als dimensionslose Zahlen zwischen Null und Eins.
|
Da hast du etwas gründlich mißverstanden. Verwechselst du den Erwartunsgwert mit Wahrscheinlichkeiten?
In Anführungszeichen habe ich ihn übrigens nur gesetzt, um mich von der statistischen Interpretation des Begriffes zu distanzieren.
| Zitat: |
Dass man aus dem mathematischen Formalismus der Quantenmechanik alles mögliche herausdeuten kann, ist mir bekannt, und meinetwegen mag man da herausdeuten, dass man Quantenobjekten vor der Messung einen "Erwartungswert" für einen Energiewert oder einen Impuls, also Werte für diese Eigenschaften in einer ontologischen Schwankungsbreite, zuordnen kann.
|
Da gibt es nicht viel zu deuten. Das ist ein Fakt, der völlig ohne Umschweife aus dem Formalismus folgt. (Bis auf das "ontologisch" natürlich, was aber nicht von mir stammt.) Der Streitpunkt ist höchstens, was diese Werte dann am Ende mit Messergebnissen zu tun haben. Daß die Theorie diese Frage nicht auf dieser fundamentalen Ebene beantworten kann, sollte einen allerdings nicht weiter verwundern. Viele der Interpretationsprobleme rühren anscheinend daher, daß versucht wird, die Antwort dieser Frage in die Grundpostulate der Theorie aufzunehmen.
| Zitat: |
Aber das widerspricht ja meiner Behauptung nicht, dass das Objekt vor der Messung keine physikalischen Eigenschaften hat, mit denen es zu einem Objekt mit persistierenden Eigenschaften würde, die es identifizierbar machen. Es ist ja hinsichtlich seiner Eigenschaften dann immer noch unscharf.
|
Selbstverständlich widerspricht das deiner Behauptung. Du hast dieselben Eigenschaften der klassischen Theorie wie Ort, Impuls, Drehimpuls, Energie etc. auch in der nichtrelativistischen QM. Der Unterschied ist nur, daß diese Eigenschaften dort anderen Gesetzen folgen. Das ist natürlich wenig überraschend. Wenn diese Größen als "persistente" und "identifizierende" Eigenschaften nicht ausreichen, dann sprichst du damit also kein spezifisches Problem der QM an.
Hinzu kommen noch Eigenschaften, die es in der klassischen Physik nicht gibt, wie z.B. alle Unschärfen dieser Größen.
Über alle diese Größen macht die Theorie aber deterministische, eindeutige Aussagen. Es handelt sich also um sehr wohldefinierte Eigenschaften von Quantenobjekten.
| Zitat: |
Ich denke mal, da wirst der These zustimmen, dass - wenn die Schrödingergleichung überhaupt irgend was beschreibt - dass sie dann das beschreibt, womit man ein Quantenobjekt vor der Messung identifizieren kann (was seine Identität "ausmacht"). Sie würde ja sonst - ja was ? - beschreiben ? Es gibt dann zwei Aspekte, und zwar der Aspekt der ontischen Eigenschaften des Objekts und der der (spezifischen) Wirkung des Objekts. Beide können operativ der Identifizierung dienen (müssen nicht unbedingt kategorial verschieden sein). Im Fall eines freien Teilchens gibt es aber keine Wirkung, daher können nur Eigenschaften operativ zur Identifikation dienen.
Folglich muss die Schrödingergleichung für ein freies Quantenobjekt die das Objekt identifizierenden Eigenschaften beschreiben.
|
Das folgt überhaupt nicht. Die Schrödingergleichung beschreibt nur die Zeitentwicklung des Zustands eines abgeschlossenen System (im Schrödingerbild, wie man dazusagen muß). Daneben gibt es noch die Observablenalgebra und die Zeitentwicklung der darin enthaltenen Operatoren (ist im Schrödingerbild trivial). Die Eigenschaften des Systems ergeben sich erst aus dem Zustand und der Observablenalgebra zusammen. Die Schrödingergleichung liefert dir dann die Zusatzinformation, wie sich diese Eigenschaften mit der Zeit ändern.
| Zitat: |
Wir müßten darüber erst mal Einigkeit herstellen. Wenn Du meinst, das sei nicht der Fall, dann müßtest Du sagen, was sie anderweitig beschreibt. Mit beschreiben meine ich, dass sie d a r ü b e r etwas verschlüsselt aussagt - aber eben auch nicht mehr. Und das man das entschlüsseln muss.
Es stellen sich doch zwei Fragen: Welche Eigenschaften sind das ? Und wie macht sie das, oder anders gesagt, wie entschlüsselt man das ?
|
Ich denke, daß ich das bereits getan habe. Du scheinst die Antwort entweder nicht zur Kenntnis zu nehmen oder unzufrieden damit zu sein.
| Zitat: |
Und ich behaupte nun, die einzige Eigenschaft, der man sich sicher sein kann, dass das Quantenobjekt diese immer hat, und über die die Schrödingergleichung uns etwas sagen m u s s , ist die Fähigkeit zu einer Wirkung. Das heißt nicht, dass ein Quantenobjekt immer eine Wirkung ausübt - das eben nicht - sondern nur, dass es diese Fähigkeit hat.
[...]
Diese Potenz zur Wirkung hat jedes Quantenobjekt. Falls Du hier Zweifel hast, wäre es gut, Du würdest das sagen. Man kann sich seiner Sache ja nie sicher sein.
|
Ok, von mir aus hat jedes Quantenobjekt die "Potenz zur Wirkung". Diese Erkenntnis wird dich aber nicht sehr weit bringen, fürchte ich.
| Zitat: |
Wenn also die Fähigkeit zu einer Wirkung dem Quantenobjekt notwendigerweise innewohnt, als gleichbleibendes Identifikationsmerkmal, w i e beschreibt die Schrödingergleichung das ? Wie kann ich das aus ihr direkt oder aus ihren Lösungen herauslesen, wenn sie ein Objekt beschreibt, das diese Potenz einfach nur hat, und diese Potenz überhaupt nicht realisiert.
|
Die Schrödingergleichung beschreibt die Potenz zur Wirkung mit Hilfe eines Potentials V(x), also z.B. so
}{\partial t} = -\frac{\hbar^2}{2m}\Delta\psi(x,t) + V(x)\psi(x,t).)
Ob diese Potenz auch "realisiert" ist, hängt natürlich von V(x) und von 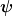 ab. Wenn z.B. V im Unendlichen schnell genug abfällt und sich ab. Wenn z.B. V im Unendlichen schnell genug abfällt und sich 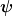 nur dort lokalisiert, wo V verschwindet, dann hat das Objekt seine Potenz zur Wirkung noch nicht realisiert. nur dort lokalisiert, wo V verschwindet, dann hat das Objekt seine Potenz zur Wirkung noch nicht realisiert.
Wenn hingegen V(x) überall null ist, dann besitzt dieses Objekt diese Potenz gar nicht.
| Zitat: |
Das was das Objekt zu einem Individuum macht, ist doch zweierlei, einmal das es diese Potenz hat, und dass es diese permanent hat. Beides muss in der Schrödingergleichung oder in ihren Lösungen abgebildet sein.
|
Ich würde denken, was ein Objekt zum Individuum macht, ist jede Menge von Eigenschaften, mit der man es eindeutig von anderen Objekten unterscheiden kann. Aber wie dem auch sei, die Schrödingergleichung bildet auf jeden Fall die "Potenz zur Wirkung" eines Systems ab.
| Zitat: |
Ich behaupte nun, dass es dadurch abgebildet ist, dass die ebene Welle als Lösung Identitätsoperationen darstellen, mit E/h*t und p/h*x als Parameter (im Dreidimensionalen, weil hier der Konfigurationsraum der 3-dim. Raum entspricht, mit t als Zeitparameter).
|
Das klingt in meinen Ohren einfach nach Kauderwelsch.
| Zitat: |
Bitte sage mir, wenn dies physikalischen Erkenntnissen widerspricht, was das genau ist - nicht, dass man die Schrödingergleichung und ihre Lösung für ein freies Teilchen auch anders interpretieren kann, oder dass dies gängigerweise so gemacht wird - sondern welche Erkenntnis diese - von mir in den Raum gestellte These - These h i n f ä l l i g macht.
Ich will mich nicht festbeißen, man muss ja kritisch bleiben. Aber Deine Einwände treffen bisher irgendwie nicht den Punkt.
|
Das mag schon sein. Beantwortet habe ich natürlich nur, was mir verständlich war. Darunter befanden sich für mich ein paar kritikwürdige Punkte, auch wenn sie dir vielleicht nicht so wesentlich waren.
Der Teil, der anscheinend deine Hauptthese ausmacht, ist, in aller Offenheit, ein inkohärenter Schlamassel, in dem du wahllos mathematische Konzepte aneinanderreihst, die du nicht gut verstanden hast. Ich habe versucht dir ein wenig klar zu machen, warum das alles dort keine Sinn ergibt. Aber das schien dich nicht weiter zu stören. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 10. Mai 2020 11:56 Titel: TomS Verfasst am: 10. Mai 2020 11:56 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Folglich muss die Schrödingergleichung für ein freies Quantenobjekt die das Objekt identifizierenden Eigenschaften beschreiben. Wir müßten darüber erst mal Einigkeit herstellen.
Welche Eigenschaften sind das ? |
1) Zunächst solltest du den Rahmen wieder spannen.
Es kann nicht nur um ein freies Quantenobjekt gehen, da ein solches in der Praxis nie existiert. Sowohl Wechselwirkung als auch Messung - unabhängig davon, in welcher Beziehung sie stehen - sollten mit betrachtet werden
Es ist a priori unklar, ob es um ein Quantenobjekt gehen sollte, in dem Sinne, dass du es von dir (dem Beobachter) oder einem größeren Quantensystem abtrennst.
Du solltest klären, welche Erwartungshaltung du explizit hast, und welche du implizit annimmst (m.E. setzt du sehr viele implizit voraus). Orientierst du dich an klassischen Vorstellungen? Möchtest du auf einen Eigenschaftsrealismus hinaus? Bist du an einer ontischen Sichtweise interessiert, oder bist du mit einer eher phänomenologischen Beschreibung von Beobachtungen bzw. Messungen zufrieden?
2) Die Schrödingergleichung alleine sagt praktisch nichts über irgendwelche Eigenschaften aus.
index_razor hat bereits darauf hingewiesen, dass du in einem abgeschlossen Quantensystem immer noch einen Satz an Observablen benötigst, die dir zusammen mit der Schrödingergleichung “Eigenschaften” des Quantensystems liefern.
Die Schrödingergleichung liefert dir für jedes beliebige Quantensystem immer das selbe fundamentale Bild: einen Zustandsvektor, dessen Zeitentwicklung eine Trajektorie auf der strukturlosen Einheitskugel in einem unendlich-dimensionalen algebraischen Raum (Hilbertraum) darstellt. Insofern sind ein freies Elektron, ein Elektron im Potential eines Atomkerns, ein Festkörper, ein zerfallendes Uranatom oder ein gemäß der QCD wechselwirkendes Quark-Gluon-Plasma mathematisch streng isomorph und physikalisch ununterscheidbar. Um sie unterscheiden zu können, um zu spezifischen Beschreibungen zu gelangen, um eine Struktur zu erhalten, um letztlich im weitesten Sinne von Eigenschaften sprechen zu können, benötigst du die Observablenalgbra.
Darüberhinaus ist klarzustellen, ob du nur abgeschlossene Quantensysteme betrachten möchtest - bis hin zum gesamten Universum - oder ob du pragmatisch auch offenen Quantensysteme untersuchen willst; letzteres lässt sich nicht auf die Schrödingergleichung reduzieren.
3) Für ein freies Quantenobjekt ist die Diskussion ziemlich irrelevant, da sie sich auf ein künstliches, isoliertes Objekt bezieht. Die Ergebnisse, die “Eigenschaften” o.ä. sind nicht beobachtbar, nicht überprüfbar, ... Wenn du also einen Bezug zur Physik als empirischer Wissenschaft herstellen möchtest, musst du die Wechselwirkung bzw. Messung mit einbeziehen. Und erst bei der Messung wird es spannend, denn über alles andere - vor bzw. ohne Messung - sind sich die Physiker ziemlich einig; jedoch ist dies irrelevant, da ohne Bezug zur Empirie. Wenn du etwas interessantes beitragen möchest, kommst du am Messproblem nicht vorbei.
4) Dass du die Konzepte und Problem der Quantenmechanik verstanden haben solltest - über die des freien Teilchens hinaus - hat index_razor ebenfalls angeführt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 10. Mai 2020 21:53 Titel: Bernd Stein Verfasst am: 10. Mai 2020 21:53 Titel: |
 |
|
Hi Tom,
es geht um eine ontische Sichtweise. Ich möchte ein Quantenobjekt als physikalischen Gegenstand konsistent und ohne Verletzung logischer Regeln beschreiben. Das ist ein berechtigtes Anliegen von jemandem, der sich Gedanken über die Welt, wie sie ist, macht, auch wenn es Leute geben mag, die von vornherein sagen, dass das sinnlos ist.
Ich frage mich also zuerst, was mir der mathematische Apparat für diese Beschreibung liefert.
Dazu hatte ich ausgeführt, dass man aus dem mathematischen Formalismus gerade das nicht herauslesen kann, dass nämlich ein Quantenobjekt im Allgemeinen, also wenn es sich nicht in einem besonderen Zustand befindet, und erst recht im Sonderfall oder in der Idealisierung als „freies Teilchen, vor einer Messung keine definierten physikalischen Eigenschaften wie Ort, Impuls oder Energie hat, und zwar deshalb, weil die Mathematik in diesem Fall über diese Bestimmungsgrößen nichts aussagt. Das bestätigst Du mir ja, wenn Du sagst, die Schrödingergleichung alleine sagt praktisch nichts über irgendwelche Eigenschaften aus. Das sehe ich genauso.
Das tut aber meines Erachtens auch nicht die Observablenalgebra – eben wenn es sich nicht um Sonderfälle handelt, und das tun auch ihre Lösungen nicht. Es geht immer um die Beschreibung eines Quantenobjektes v o r der Messung. Es geht mir nicht darum, herauszufinden, wie ich zu Eigenschaften komme. Es geht nicht um einen Messvorgang. Es geht mir um den ontischen Zustand des Objektes v o r der Messung (außerhalb subjektiver Wahrnehmung). Ich behaupte nur, man kann einem Quantenobjekt, wenn es sich nicht in einem besonderen, zum Beispiel einem besonders präpariertem Zustand befindet, vor der Messung keine physikalische Eigenschaft zuordnen, die es individuieren. Das ist eine ganz simple Aussage: es stehen keine physikalischen Eigenschaften zur Verfügung (kein Ort, kein Impuls, kein Drehimpuls, kein Energiewert – im Allgemeinen, also außerhalb besonderer Präparationen, und außerhalb besonderer Rahmenbedingungen) – wo sollen diese Eigenschaften herkommen. Ich meine damit – wie oben gesagt – definierte Eigenschaften, also eine feste reelle Zahl für den Betrag des Impulses des Objektes, eine für den Betrag der Energie, - nicht irgendwelche Streuungen. Ich wüßte nicht, wie man mit "Streuungen" von Zahlen individuieren könnte.
Du kannst natürlich sagen, es hat keinen Sinn darüber zu reden, weil ein Quantenobjekt als isoliertes Objekt in der Realität nicht vorkommt. Dann aber kann man auch in der klassischen Physik von kräftefreier Bewegung nicht reden, diese kommt nämlich auch nicht vor: ein nicht wechselwirkender Gegenstand entzieht sich auf allen Größenskalen einer Erkenntnis. Unter diesen Umständen machst Du das gesamte Konzept der speziellen Relaitivitätstheorie hinfällig, dieses beschreibt ruhende Objekte in Inertialsystemen, die nicht vorkommen.
Es kann doch nützlich sein, die grundsätzlichen Fragen an Hand reduzierter und idealisierte Situationen zu diskutieren. Das macht die Physik doch dauernd.
Bitte bedenke mein Ziel: ich möchte – da ich von Schrödinger und der Algebra nicht Brauchbares bekomme – eben unabhängig von der Theorie zunächst die fundamentalen Bestimmungsgrößen eines jeden Quantenobjektes benennen, die es deswegen hat, weil es einfach nur existiert, sozusagen als Voraussetzung seiner Existenz überhaupt (zum Beispiel dass es Teil eines Ganzen ist, dass es wechselwirken kann, zum Beispiel als Artikulation seiner Beziehung zu den anderen Teilen, dass es wenn es propagiert, das gleiche bleibt, usw.). Wenn ich diese fundamentalen Merkmale benannt habe, dann kann ich sehen, ob und wo sich diese in der Schrödingergleichung, der Algebra und in dem ganzen mathematischen Apparat wiederspiegeln. Wenn ich ihre Entsprechung dort gefunden habe, falls es diese dort gibt, dann kann ich weiterfragen, wie wird diese Entsprechung als Teil der Mathematik üblicherweise von der Physik interpretiert.
Ich hinterfrage dann die Interpretation der Mathematik auf diese meine Weise.
Das ist der Weg, ob ich dabei immer richtig vorgehe, weiss ich nicht, Du kannst mir aber helfen, indem Du mir sagst, an welchen Stellen meiner Behauptungen ich im Widerspruch zu gesicherter Erkenntnis des Physik stehe. Ansonsten gehe ich logisch deduktiv vor. Dabei geht es nicht darum, ob Du die Sache anders siehst, davon muss ich sowieso ausgehen, es gibt immer mehrere Sichtweisen auf ein und dieselbe Sache, sondern ob meine Sicht zu einem Widerspruch mit gesicherten Erkenntnissen führt. Was Index Razor dazu ausführt, entzieht sich allerdings meinem Verstehen.
Grüße
Bernd |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 10. Mai 2020 22:49 Titel: TomS Verfasst am: 10. Mai 2020 22:49 Titel: |
 |
|
Ein ontischer Zugang ist für mich schon in Ordnung.
Ein Ausblenden des Messproblems führt m.E. in eine Sackgasse, aber lassen wir das beiseite.
Das Ausblenden der Observablenalgebra und die von dir gezogenen Schlüsse sind m.E. problematisch:
Betrachten wir den Kern des quantenmechanischen Formalismus. Die Formulierung der Regeln ist mathematisch einfach gehalten, es existieren Verallgemeinerungen bzw. Präzisierungen ¹.
Kursiv gesetzter Text bezieht sich auf reale Systeme und deren Dynamik, Präparation und Messung, sowie tatsächlich messbare Größen d.h. Observablen sowie deren Messwerte.
Normal gesetzter Text bezieht sich auf rein mathematische Objekte, die die o.g. physikalischen Systeme etc. in gewissem Sinne repräsentieren ².
Die folgenden Regeln sind identisch zu den etablierten Regeln ³ der 'orthodoxen Formulierung', jedoch ohne Betrachtung der Messung.
1. Die Beschreibung eines Quantensystems erfolgt im Rahmen eines separablen Hilbertraumes 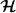
2. Der Zustand eines einzelnen ⁴ Quantensystems wird vollständig durch einen normierten Vektor ⁵ 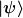 als Element dieses Hilbertraumes als Element dieses Hilbertraumes 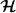 beschrieben. beschrieben.
3. Die Zeitentwicklung eines einzelnen isolierten ⁶ Quantensystems wird durch einen unitären Zeitentwicklungsoperator
 = e^{ -\mathrm{i}Ht })
mittels
\rangle = U(t)\,|\psi(0)\rangle)
beschrieben; 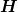 ist dabei der Hamiltonoperator. ist dabei der Hamiltonoperator.
Diese Regel ist vollständig äquivalent zur Schrödingergleichung ⁷
 \rangle = H \, |\psi(t) \rangle)
4. Eine beobachtbare Größe, d.h. eine Observable eines Quantensystems wird durch eine selbstadjungierten ⁸ Operator  repräsentiert, der auf die Zustandsvektoren repräsentiert, der auf die Zustandsvektoren 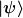 in in 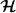 wirkt. wirkt.
--------------------
¹ U.a. für entartete Unterräume, verallgemeinerte Messungen die nicht mittels Projektoren sondern positiver operatorwertiger Wahrscheinlichkeitsmaße (POVM) beschrieben werden, Darstellungen von Zuständen als Strahlen (Rays) bzw. in projektiven Hilberträumen, verallgemeinerte Zustände und Dichteoperatoren, kontinuierliche bzw. distributionswertige Basen, Gelfand Triples bzw. rigged Hilbert spaces. Für eine Einführung sind diese Details oft irrelevant – mit einer Ausnahme, nämlich den kontinuierlichen bzw. distributionswertige Basen für Orts- und Impulsraumdarstellung
² Die Bedeutung des Formalismus und der Repräsentation (ontisch, rein instrumentalistisch etc.) sowie die einzelnen Interpretationen der Quantenmechanik sind hier nicht Gegenstand. Allerdings dienen die Regeln als gemeinsamer Startpunkt für die wesentlichen Interpretationen, wobei diese je nach Interpretation teilweise angepasst werden.
³ Diese etablierten Regeln sind Gegenstand einiger Lehrbücher, z.B. Dirac, Cohen-Tannoudji, Sakurai, Weinberg, Griffiths, …
⁴ In statistischen bzw. Ensemble-Interpretationen wird dies dahingehend modifiziert, dass der Zustandsvektor nicht mehr ein einzelnes System repräsentiert, sondern lediglich ein Ensemble gleichartig präparierter Systeme. Dies spielt im Folgenden keine Rolle
⁵ Präziser ist die Formulierung der Repräsentation mittels einer Äquivalenzklasse  mit mit  und dem o.g. normierten Vektor und dem o.g. normierten Vektor 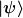 in in 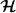 . .
Dies ist automatisch gegeben bei Verwendung projektorwertiger Zustände 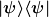 , insbs. bei der Betrachtung verallgemeinerter Zustände bzw. Dichteoperatoren. , insbs. bei der Betrachtung verallgemeinerter Zustände bzw. Dichteoperatoren.
⁶ Für nicht-isolierte Systeme wäre der Hamiltonoperator  ) zeitabhängig; dies spielt im Folgenden keine Rolle. zeitabhängig; dies spielt im Folgenden keine Rolle.
⁷ Diese Regel gilt im sogenannten Schrödinger-Bild. Es existieren andere, unitär-äquivalente Formulierungen, insbs. das Heisenberg- und das Wechselwirkungsbild, in denen die Zeitentwicklung vollständig oder teilweise von den Zustandsvektoren auf die Operatoren übertragen wird; letzteres spielt im Folgenden keine Rolle.
⁸ Ich bevorzuge die mathematische Bezeichnung ‚selbstadjungiert‘ und die klare Abgrenzung zu ‚symmetrisch‘; im endlich-dimensionalen Fall sind beide Bedeutungen identisch.
--------------------
Soweit, so gut.
Nun könntest du den Punkt 4 einfach beiseite lassen. Du hast jedoch immer zumindest einen minimalen Satz an Observablen, nämlich mit dem Zustandsvektor auch die Familie der Projektoren
\rangle\langle\psi(t)| )
sowie mit dem Zeitentwicklungsoperator
 = e^{ -\mathrm{i}Ht })
den Hamiltonoperator  . .
Darüberhinaus ist mit jeder Hilbertraumbasis
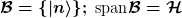
auch eine (unendliche) Familie von Observablen mittels reeller Koeffizienten a

verknüpft.
Das heißt, diese Observablen sind einfach da, ob du nun willst oder nicht. Was fehlt ist evtl. eine geeignete physikalische Interpretation. Sie enthalten in der Praxis u.a. Ort, Impuls, Energie, …
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Mai 2020 07:56 Titel: index_razor Verfasst am: 11. Mai 2020 07:56 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: |
es geht um eine ontische Sichtweise. Ich möchte ein Quantenobjekt als physikalischen Gegenstand konsistent und ohne Verletzung logischer Regeln beschreiben. Das ist ein berechtigtes Anliegen von jemandem, der sich Gedanken über die Welt, wie sie ist, macht, auch wenn es Leute geben mag, die von vornherein sagen, dass das sinnlos ist.
|
Um das klarzustellen: Das Anliegen ist nicht sinnlos, nur deine Durchführung ist es. Allerdings bist du natürlich leider, in typischer Crank-Manier, völlig immun gegen diese Einsicht.
| Zitat: |
Ich frage mich also zuerst, was mir der mathematische Apparat für diese Beschreibung liefert.
Dazu hatte ich ausgeführt, dass man aus dem mathematischen Formalismus gerade das nicht herauslesen kann, dass nämlich ein Quantenobjekt im Allgemeinen, also wenn es sich nicht in einem besonderen Zustand befindet, und erst recht im Sonderfall oder in der Idealisierung als „freies Teilchen, vor einer Messung keine definierten physikalischen Eigenschaften wie Ort, Impuls oder Energie hat, und zwar deshalb, weil die Mathematik in diesem Fall über diese Bestimmungsgrößen nichts aussagt.
|
Nochmal, das ist falsch. Die Mathematik der QM macht gerade über alle diese Größen in jedem Zustand, zu jedem Zeitpunkt (insbesondere vor einer Messung) konkrete Aussagen.
Die Frage ist nur, wie man diese Werte interpretiert. Da hat sich nun die Ansicht durchgesetzt, daß sie nicht die realen Eigenschaften eines individuellen Systems repräsentieren. Das liegt aber nicht daran, daß es sie gar nicht gibt, sondern nur daran, daß davon ausgegangen wird, nur Eigenwerte von Observablen könnten solche Eigenschaften repräsentieren. Das eröffnet folgenden Lösungsansatz für dein Anliegen: man gibt die Annahme auf, daß nur Eigenwerte reale Eigenschaften repräsentieren.
Ich weiß, dich interessieren nur Kommentare zu deinem eigenen Ansatz. Du solltest aber auch nicht von der falschen Voraussetzungen ausgehen, daß "die Mathematik" nichts über diese Größen aussagt.
| Zitat: |
Das bestätigst Du mir ja, wenn Du sagst, die Schrödingergleichung alleine sagt praktisch nichts über irgendwelche Eigenschaften aus. Das sehe ich genauso.
|
Die Mathematik der QM besteht eben nicht nur aus der Schrödingergleichung.
| Zitat: |
Ich behaupte nur, man kann einem Quantenobjekt, wenn es sich nicht in einem besonderen, zum Beispiel einem besonders präpariertem Zustand befindet, vor der Messung keine physikalische Eigenschaft zuordnen, die es individuieren. Das ist eine ganz simple Aussage: es stehen keine physikalischen Eigenschaften zur Verfügung (kein Ort, kein Impuls, kein Drehimpuls, kein Energiewert – im Allgemeinen, also außerhalb besonderer Präparationen, und außerhalb besonderer Rahmenbedingungen) – wo sollen diese Eigenschaften herkommen. Ich meine damit – wie oben gesagt – definierte Eigenschaften, also eine feste reelle Zahl für den Betrag des Impulses des Objektes, eine für den Betrag der Energie, - nicht irgendwelche Streuungen.
|
Und wofür hältst du z.B.
 = \int\dd^3 x\ \vec{x} |\psi(\vec{x},t)|^2 )
 = -i\hbar\int \dd^3 x\ \psi^\star(\vec{x},t)\nabla \psi(\vec{x},t))
etc? Das sind zu jeder Zeit t jewels 3 feste reelle Zahlen mit Einheiten für die beiden physikalischen Größen Ort und Impuls. Genau wie es sein muß. Drei weitere Zahlen gibt es für die Komponenten des Drehimpulses und eine weitere für die Energie. Diese Zahlen beschreiben auch keine Streuungen.
Auf wieviele verschiedene Arten muß man dir die Existenz dieser Größen noch unter die Nase reiben, bis du aufhörst zu fragen, woher sie kommen sollen?
| Zitat: |
Ich wüßte nicht, wie man mit "Streuungen" von Zahlen individuieren könnte.
|
Das weiß wohl niemand. Da "'Streuungen' von Zahlen" allein deine Erfindung sind, müssen wir dieses Problem aber nicht lösen.
| Zitat: |
Ich hinterfrage dann die Interpretation der Mathematik auf diese meine Weise.
Das ist der Weg, ob ich dabei immer richtig vorgehe, weiss ich nicht, Du kannst mir aber helfen, indem Du mir sagst, an welchen Stellen meiner Behauptungen ich im Widerspruch zu gesicherter Erkenntnis des Physik stehe. Ansonsten gehe ich logisch deduktiv vor.
|
Nein, das tust du nicht, auch wenn es sich für dich so anfühlt. Dein Vorgehen aus dem Eröffnungsbeitrag kann man bestenfalls als lose Assoziation von Begriffen beschreiben. Angesichts der relativ inhaltsleeren Formulierung deiner Voraussetzungen a) - c) ist es auch weitgehend ausgeschlossen, daß daraus etwas konkretes über irgendeine Lösung der Schrödingergleichung deduziert werden kann. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 11. Mai 2020 17:17 Titel: Bernd Stein Verfasst am: 11. Mai 2020 17:17 Titel: |
 |
|
Hi Tom,
Du schreibst:
"Das heißt, diese Observablen sind einfach da, ob du nun willst oder nicht. Was fehlt ist evtl. eine geeignete physikalische Interpretation. Sie enthalten in der Praxis u.a. Ort, Impuls, Energie, …"
Ja, das ist mir klar, und ich sehe das genauso, es ist eine Frage der Interpretation, was diese Observablen für die Identifikation des Quantenobjekts oder -systems bedeuten. Auch index razor hat da seine eigene Interpretation, die ich übernehmen soll, was ich aber natürlich nicht muss.
Jede Interpretation gründet auf bestimmten metaphysischen Voraussetzungen, und wenn ich eine bestimmte Interpretation verteidige, muss ich diese Voraussetzungen nennen, und alle Schlussfolgerungen. Ich will das jetzt mal versuchen. Ich interpretiere die qm Algebra, um die es hier geht, so, dass der ganze Apparat (Schrödingergleichung und Algebra) nur mögliche Meßwerte vorhersagt, und das Objekt daher unbestimmt ist und bleibt. Wie ist das gemeint?
Es glaube es wird jetzt etwas länger:
Man muss doch zunächst fragen, was sagt die Mathematik einer (jeden) physikalischen Theorie überhaupt? Nach meiner Meinung beschreibt sie mehrere Dinge gleichzeitig. Nehmen wir zunächst eine klassische Theorie, zum Beispiel die Gleichung für die Wurfparabeln, allgemein x(t) = f(φₒ, vₒ, g, t), (φₒ, vₒ sind Anfangswinkel und Anfangsgeschwindigkeit, g und t selbsterklärend). Was beschreibt diese Gleichung? Sie beschreibt eine Wurfparabelschar, die Gesamtheit aller Wurfparabeln. Ist das, was ich „Gesamtheit“ genannt habe, etwas Reales, oder ist das eine Gedankenkonstruktion, ein mathematisches Artefakt, oder ein Vektor in einem hochdimensionalen Konfigurations- oder Phasenraum ? W a s also beschreibt die Gleichung ? Wer hat darauf eine klare Antwort ?
Ich habe dabei nur gefragt, was die Gleichung in ihrer allgemeinen Form beschreibt. Wenn ich natürlich Randbedingungen berücksichtige, die variablen Anfangswerte und den Zeitparameter t also durch feste Werte ersetze, beschreibt sie einen Ort, also einen realen Wert, der als Meßwertvorhersage angesehen werden kann. Ohne Randbedingungen kann man sie durchaus so interpretieren, dass sie garnichts Reales beschreibt. Man könnte durchaus sagen, sie beschreibt die Freiheiten des Wurfobjektes für den Fall, dass diese Freiheiten nicht durch Randbedingungen eingeschränkt sind. Sind Freiheiten etwas Reales ? Oder stellt der Phasenraum die Menge aller Freiheiten dar ?
Um das zu klären, schreibe ich jetzt die Gleichung um in x(t) = R(φₒ, vₒ, tₒ) f(φₒ, vₒ, g, t). R nenne ich „Randbedingungs-Einsetz-Operator“, er soll nämlich die algebraische Operation symbolisieren, feste Werte an Stelle der Variablen in die Gleichung einzusetzen. Dieser Operator spiegelt dann die Randbedingungen des Parabelwurfs wider, zum Beispiel die apparativen Randbedingungen im Fall, dass ich das Durchlaufen einer bestimmten Wurfparabel unter einem bestimmten Winkel und mit bestimmter Anfangsgeschwindigkeit experimentell realisiere. Kurzum, um es nicht zu lang werden zu lassen:
In dieser Form (mit R) sagt mir die Gleichung dreierlei:
a) die allgemeine Gleichung ohne Randbedingungen beschreibt die generellen Freiheiten des Systems (die Gesamtheit aller möglichen Bahnen).
b) R symbolisiert die apparativen (äußeren) Einschränkungen der Freiheiten
c) die algebraische Operation mit R kann die Freiheiten teilweise oder maximal einschränken (je nach Form). Im Fall dass keine Freiheiten mehr da sind (alle Anfangs- und Randbedingungen vollständig eingesetzt) erhalte ich einen Vorhersagewert (für den Ort), das ist eine reelle Zahl, die das Objekt unter diesen Randbedingungen individuiert. In gewissem Sinn beschreibt die Gleichung mit dem Operator zusammen auch eine Messung, und zwar deshalb, weil der Randbedingungs-Operator auch das maximale Einschränken der Freiheiten durch eine Apparatur in der Gleichung abbildet.
Messen heißt, so gesehen: apparatives Beseitigen von Unbestimmtheiten, und zwar Unbestimmtheiten, die daher rühren, dass das Objekt mehrere Freiheiten (mehrere Möglichkeiten) hat, einen Ort zu haben, einen Impuls oder einen Energiebetrag zu übertragen. Das ist keine epistemische Unbestimmtheit, sondern eine ontologische Unbestimmtheit in dem Sinne, das etwas unbestimmt ist, weil die Randbedingungen mehrere Möglichkeiten zulassen, das Objekt so oder so individuiert sein kann. Wenn ich also ein Objekt beschreiben will, dann kann ich dies nur dadurch tun, dass ich es in einer Situation beschreibe, in der es keine anderen Freiheiten des SoSeins mehr hat, das SoSein ist dann nicht mehr unbestimmt, sondern bestimmt und die zugehörigen Größen individuieren das Objekt (wird normalerweise sillschweigend vorausgesetzt).
Die Parallelen zur Quantentheorie sind augenfällig. Durch die Schrödingergleichung im allgemeinen Fall (ohne Randbedingungen) werden die Zeitentwicklungen alle Zustandsvektoren – wie du super treffend beschrieben hast – auf der strukturlosen Einheitskugel in einem unendlich-dimensionalen algebraischen Raum (Hilbertraum) „als Gesamtheit“ abgebildet. In meiner etwas naiven Redeweise sind diese Zustandsvektoren nichts anderes als die Gesamtheiten aller Freiheiten, die Quantenobjekte haben können. Unabhängig von der Schrödingergleichung gibt es dann eine Algebra, die nichts anderes macht, als die apparativen Einschränkungen (Umgebungs-, Anfangs-, Randbedingungen) mittels Operatoren zu beschreiben (analog R im klassischen Fall), nur dass hier der Raum der Freiheiten ein anderer ist, als im klassischen Fall, d.h. eine andere Struktur hat. Ein Operator H in geeigneter Form, kann maximale apparative oder äußere Einschränkungen dieser Freiheiten symbolisieren. Maximale Einschränkungen heisst hier: Schrödingergleichung und Algebra mit geeigneten maximal Freiheit-einschränkenden Operatoren sagen uns: dieses Quantensystem hat eben n i c h t unendlich viele, sondern nur noch ganz bestimmte Freiheiten, mehrere Möglichkeiten für einen Ort, mehrere Freiheiten der Entwicklung, eben bestimmte Auswahl - es sind nicht beliebig viele wie ohne Spezifizierung von H , sondern ganz bestimmte Werte für die betrachtete Eigenschaft (Messgröße) von den Randbedingungen zugelassen (Eigenwerte). Damit ist das Objekt unbestimmt im oben genannten ontologische Sinn, nämlich insofern, als es sich um eine Unbestimmtheit handelt, die darin besteht, das nicht einer, sondern mehrere mögliche Werte einer physikalischen Größe von den äußeren Bedingungen erlaubt sind.
Dass der Mannigfaltigkeitsraum der Freiheiten des Objekts, den die Schrödingergleichung beschreibt, eine andere Struktur hat, als der dreidimensionale Raum der Freiheiten in der klassischen Physik (es gibt hier immer nur eine einzige Freiheit für den nächsten Schritt) ist klar, aber es ist in erster Linie eine andere logische Struktur, die hier innewohnt. Das drückt sich in den nicht kommutierenden Operatoren aus. Ein Gegenstand kann nicht an einem Ort verharren, und sich gleichzeitig bewegen (es gibt keine Randbedingungen, die die Ortsfreiheit maximal einschränken und gleichzeitig maximale Freiheiten der Bewegung ermöglichen). Es kann auch nicht einen Energiebetrag zum Zeitpunkt t an einen anderen Gegenstand abgeben, wenn es zur Energieübertragung eine Zeit n*T = n*h/E braucht. Bestimmte Kombinationen von Freiheiten sind aus logischen Gründen im Raum der Freiheiten halt ausgeschlossen, was sich in der mathematischen Beschreibung des Raumes durch nicht kommutierende Operatoren für die Randbedingungen widerspiegelt. Man kann viele algebraische Besonderheiten, die diesen Raum vom klassischen Phasenraum unterscheiden, hier aus der Logik der Freiheitsbeschränkungen erklären. In der Klassischen Physik gibt es solche Ausschlüsse auch, zum Beispiel gibt es keine Randbedingungen, die einem Gegenstand erlauben, sich gleichzeitig in zwei Richtungen zu bewegen, aber im Freiheitenraum der Quantenobjekte gibt es eben viele logische Einschränkungen, zum Beispiel gibt es dort auch keine Lokalität, weil bei einer Änderung äußerer Bedingungen Freiheiten instantan im ganzen Raum wegfallen können.
Die Mathematik der Quantenmechanik beschreibt nach dieser Lesart immer noch einen Vektor in einem Hilbertraum, aber man kann diesen Vektor auch als Freiheit in einem Raum der Freiheiten interpretieren. In diesem Sinne sagt uns die Mathematik nichts über die Eigenschaften eines Quantenobjekts aus, weil sie eben diese Objekte gar nicht beschreibt, und weil eben der Vektor nicht mit einem Objektzustand, sondern nur mit dessen Freiheiten in Bezug gesetzt werden darf. Weil diese Mathematik, selbst dann, wenn sie die maximal spezielle Situation beschreibt, also unter maximal einschränkenden Randbedingungen, immer noch mehrere Freiheiten, oder mehrere Möglichkeiten dafür zulässt, dem betrachteten Objekt einen bestimmten Wert einer Meßgröße zuschreiben zu können. Es ist wie gesagt eine Unbestimmtheit, weil – solange es nicht zu einem Meßvorgang kommt - immer (!) mehrere Möglichkeiten zugelassen sind (bezeichne ich als ontische Unbestimmtheit). Wenn ein Objekt zwei Möglichkeiten für eine Bahn hat, wenn es zwei Möglichkeiten hat, einen Ort einzunehmen, dann ist es immer noch hinsichtlich des Ortes unbestimmt, auch wenn alle diese Orte existieren.
Es ist genau diese Unbestimmtheit, die durch einen Messvorgang beseitigt wird. Der hat mit der SG und der algebraischen Handhabung von Freiheiten nichts zu tun. Die Unbestimmtheit wird von Randbedingungen beseitigt, die nicht durch die Mathematik oder durch einen Operator „kontrollierbar“ sind.
Damit ist nur dargelegt, was die SG und die Algebra nach meinem Dafürhalten aussagt. Sie liefern nicht mehr als mehrere Möglichkeiten für einen Wert, sie liefern also nichts Bestimmtes. Ich kann das alles auch präzisieren, aber ich will erst mal abwarten, was Du zu dieser (eigenwilligen) Interpretation sagst. Es ist jedenfalls ein gutes Zeichen, dass Du die Grundlagen des Ganzen ansprichst, und insbesondere die Frage, wie man die Algebra verstehen soll, auch wirklich stellst (und nicht deren Interpretation vorgibst, oder Noten austeilst, wenn man sich dieser nicht anschließt). Also das war meine Antwort, sorry ist etwas lang geworden.
Grüße Bernd |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Mai 2020 17:34 Titel: index_razor Verfasst am: 11. Mai 2020 17:34 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: |
Ja, das ist mir klar, und ich sehe das genauso, es ist eine Frage der Interpretation, was diese Observablen für die Identifikation des Quantenobjekts oder -systems bedeuten. Auch index razor hat da seine eigene Interpretation, die ich übernehmen soll, was ich aber natürlich nicht muss.
|
Schon wieder falsch. Meine Kritik bezieht sich auf deine Behauptung über den mathematischen Formalismus. Du schreibst (meine Hervorhebung),
| Zitat: |
Dazu hatte ich ausgeführt, dass man aus dem mathematischen Formalismus gerade das nicht herauslesen kann, dass nämlich ein Quantenobjekt im Allgemeinen, also wenn es sich nicht in einem besonderen Zustand befindet, und erst recht im Sonderfall oder in der Idealisierung als „freies Teilchen, vor einer Messung keine definierten physikalischen Eigenschaften wie Ort, Impuls oder Energie hat, und zwar deshalb, weil die Mathematik in diesem Fall über diese Bestimmungsgrößen nichts aussagt.
|
Dann verlangst du andererseits von diesen "Bestimmungsgrößen" nichts anderes, als daß sie konkrete reelle Zahlen sind. Also zeige ich dir konkrete reelle Zahlen die direkt aus dem mathematischen Formalismus der QM folgen. Damit ist deine Aussage schon widerlegt.
Mir ist völlig egal wie du diese Zahlen dann interpretierst. Von mir aus kannst du dich auf den Standpunkt stellen, daß die von mir angegebenen Zahlen nicht als "persistierende", "individuierende" oder -- was auch immer -- Bestimmungsgrößen für Quantenobjekte geeignet sind. Aber du mußt dazu sagen, daß diese Aussage auf einer bestimmten Interpretation dieser Größen beruht. Auf ihre Abwesenheit im mathematischen Formalismus kannst du dich dafür nicht berufen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 11. Mai 2020 18:43 Titel: TomS Verfasst am: 11. Mai 2020 18:43 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | | es geht um eine ontische Sichtweise. Ich möchte ein Quantenobjekt als physikalischen Gegenstand konsistent und ohne Verletzung logischer Regeln beschreiben. |
| Bernd Stein hat Folgendes geschrieben: | | Ich interpretiere die qm Algebra, um die es hier geht, so, dass der ganze Apparat (Schrödingergleichung und Algebra) nur mögliche Meßwerte vorhersagt, und das Objekt daher unbestimmt ist und bleibt. |
Es führt zu nichts, wenn wir hier ständig über Widersprüche stolpern: erst ontisch, dann positivistisch / instrumentalistisch.
Der Rest zeigt - leider - dass du die Quantenmechanik neu interpretieren möchtest, ohne ihren unbestrittenen Kern verstanden zu haben.
Mein Tipp: lerne zunächst die Mathematik der Quantenmechanik, die du für ein Grundverständnis benötigst, und mache dich mit einigen etablierten Interpretation und deren Problemen vertraut.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 11. Mai 2020 19:04 Titel: Bernd Stein Verfasst am: 11. Mai 2020 19:04 Titel: |
 |
|
Hi index razor,
es könnte gut sein, dass wir eigentlich gar keine Differenzen haben. Ich verwende alle Begriffe in ihrer üblichen umgangssprachlichen Bedeutung. Nehmen wir folgende Situation: Es gibt Otto und mich mit folgenden Randbedingungen: Otto hat mir gesagt, dass er nach Köln und Paris fahren will, nun ist er weggefahren, er hat mir aber nicht gesagt, wo er zuerst hinfährt. Es gibt zu einem Zeitpunkt nach seiner Abfahrt unter diesen Randbedingungen jetzt gleichzeitig zwei Möglichkeiten für seinen Aufenthalt, auch wenn er sich nur an einem Ort aufhalten kann. Den Ort kann ich durch eine reelle Zahl (einen Abstand) indentifizieren, die beiden möglichen Aufenthaltsorte durch zwei reelle Zahlen, die beiden Möglichkeiten, die gleichzeitig nebeneinander existieren, können aber nicht gleichzeitig realisiert sein, sie sind nicht mit reellen Zahlen quantifizierbar, ihre Menge bildet einen abtstrakten algebraischen Raum mit zwei Dimensionen (so was wie einen Spinraum), mit einer bestimmten Struktur. Du wirst diese Situation viel besser mathematisch beschreiben können als ich, ich bin mathematisch unbegabt.
Ich behaupte nun, dass für mich, der ich etwas über Otto aussagen will, der den Ort von Otto identifizieren will, dass für mich dieser Aufenthaltsort von Otto unbestimmt ist, dass ich ihn nicht beschreiben kann, obwohl dieser Ort objektiv existiert. Es kommt nicht darauf an, ob die Eigenschaft, dass etwas an einem Ort sein kann, schon existiert oder nicht. Es kommt nicht darauf an, ob ein Objekt eine Energie oder einen Impuls einfach nur haben k a n n , auch nicht, ob die zugehörigen reellen Werte nur innerhalb bestimmter Grenzen liegen. Es kommt darauf an, ob ich einem Objekt, das ich beschreiben will, e i n e n bestimmten Wert zuordnen kann (im obigen dualen Beispiel Köln oder Paris). Es ist also eine Frage der eindeutigen Zuordnung, deshalb ist in der QM der Meßvorgang auch nicht unabhängig von einer Bestimmung zu denken, worauf Tom immer rumreitet. Nur ich bin bei meiner Aussage, etwas ist unbestimmt, noch nicht bei der Frage angelangt, wie ich das Unbestimmte bestimmt machen will. Das ist noch nicht mein Thema. Es geht nur um Unbestimmtheit und seine Bedeutung unter den Rahmenbedingungen, die verschiedene Freiheiten für Otto zulassen. Die Zuordnung, die das Unbestimmte bestimmt macht, kann ich in der obigen beschriebenen Situation unter den gegebenen Randbedingungen also nicht durchführen. In d i e s e m Sinne ist der Ort von Otto unbestimmt und in seiner ontologischen Repräsentation unbeschreibbar. Ich meine nicht, dass das eine besondere Interpretation ist, sondern dass sich dies aus der üblichen Bedeutung der Begriffen für die Entitäten Ort, Möglichkeit und Unbestimmtheit ergibt. Du hast Recht, wenn Du sagst, dass man diese Sicht eigentlich erklären muss. Ich nähere mich dem Problem der Unbestimmtheit auf philosophischem Weg, Du auf dem physikalisch-mathematischen. Aber Dein Weg benötigt die Philosophie eben auch, damit keine Begriffsverwirrung entsteht, ohne metaphysische Klarstellung von Dir ist Dein Text auch nicht zu verstehen.
Grüße
Bernd |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Mai 2020 19:23 Titel: index_razor Verfasst am: 11. Mai 2020 19:23 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Es kommt darauf an, ob ich einem Objekt, das ich beschreiben will, e i n e n bestimmten Wert zuordnen kann (im obigen dualen Beispiel Köln oder Paris).
|
Dann erkläre mir doch mal genau und ohne Umschweife, was dich daran hindert, einem "Quantenobjekt" zu jeder Zeit und unabhängig von irgendeiner Messung eindeutig einen bestimmten Ort, einen bestimmten Impuls, eine bestimmte Energie, etc. zuzuordnen. Das habe ich jetzt immer noch nicht verstanden. Der mathematische Formalismus allein kann es ja nicht sein. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 11. Mai 2020 21:16 Titel: Bernd Stein Verfasst am: 11. Mai 2020 21:16 Titel: |
 |
|
Hi index razor,
ein eindeutiger Wert wird einem Quantenobjekt durch Messung zugewiesen (besondere Zwangsmaßnahmen zur Reduktion von Unbestimmtheiten).
Ein Meßvorgang wird aber von der SG und der Algebra nicht beschrieben.
SG und Algebra beschreiben immer nur die Situation v o r einer Messung, wie das Objekt v o r der Messung unter außeren Bedingungen (Einflüssen) ontologisch beschaffen ist, welches Verhalten vorher erwartet werden kann.
Die Theorie beschreibt eben nicht das, was geschieht, sondern das, was einem Geschehen (einer Beobachtung) vorausgeht, oder anders gesagt, welches Geschehen ganz allgemein auf Grund von Zwängen und Freiheiten m ö g l i c h ist - ganz egal, ob wir eine Messung dazuschalten oder nicht.
Und da ist ein Quantenobjekt anders als ein Klassisches Objekt unbestimmt in dem Sinne, dass man ihm bestimmte (eindeutige) Eigenschaften nicht zuordnen kann, eben deshalb und weil die äußeren Bedingungen im Allgemeinen immer mehrere Möglichkeiten dafür zulassen, bzw. für sein Verhalten immer noch restliche Freiheiten erlauben. Zum Beispiel hat ein Spin-1/2 Teilchen in Abwesenheit von Feldern, die an den Spin ankoppeln, zwei Möglichkeiten für die Ausrichtung seines Spins längs einer Achse. Diese beiden Freiheiten des Objekts, seinen Spin auszurichten, machen das Objekt hinsichtlich seiner Spinrichtung solange für eine Beschreibung seiner ontologischen Beschaffenheit unbestimmt, bis durch zusätzlichen Zwang (inhomog. Magnetfeld als Meßgerät) die Freiheiten des Objekts, seinen Spin beliebig auszurichten, massiv beschnitten werden, nämlich auf eine einzige Ausrichtung. Ähnlich ist es beim Durchtritt eines Objektes durch einen schmalen Spalt: die Menge an Ortsmöglichkeiten wird durch Randbedingungen auf wenige Möglichkeiten, deren Menge von der Spaltbreite abhängt, begrenzt (auf die Möglichkeiten, einen Ortswert anzunehmen aus dem Ortseigenwertsspektrum des Operators, der den Spalt mit endlicher Breite mathematisch in der Eigenwertgleichung abbildet).
Es sind immer die äußeren physikalischen (Rand)Bedingungen, die in der Realität die Freiheiten des Objektes beschneiden (die physikalische Tatsachen). Die Meßoperatoren, die diese Randbedingungen im mathematischen Formalismus abbilden, können aber - anders als in klassischen Gleichungen - nicht alle real vorkommenden und die Freiheit der Objekte begrenzenden Randbedingungen abbilden, sondern nur die Randbedingungen, die gegeben sind, bevor das Objekt mit einem Meßgerät wechselwirkt (dafür benötigt man wohl eine andere Mathematik oder Theorie). Vor der Wechselwirkung ist die Sache übersichtlich, die Randbedingungen lassen außerhalb einer solchen Wechselwirkung immer mehrere Möglichkeiten zu. Dass im Hintergrund die gesamte Physik nicht außer Kraft gesetzt ist, und alle Begriffe zur Beschreibung einer physikalischen Situation nach wie vor zur Verfügung stehen, ist doch klar. Es ist aber auch klar, dass ein Meßvorgang im atomaren und subatomaren Bereich einen ganz anderen Eingriff in die Situation darstellt, der mit den wenigen äußeren eleganten Bedingungen vorher nur gar nichts mehr gemein hat. Es ist also nicht verwunderlich, dass der ganze mathematische Apparat bis vor dem Meßvorgang gültig ist, und eine mathematische Beschreibung der notwendigerweise vor der Messung oder Wechselwirkung bestehenden Unbestimmtheiten einschließen muss.
Möglicherweise störst Du dich daran, dass diese Unbestimmtheit das Objekt zu einem Abstraktum mit ungewissem Realitätsstatus macht. das tut es aber nach meiner Auffassung ganz und gar nicht. Das Objekt springt ja nicht nach der Präparation aus der Realität heraus, weil es keine definierten Eigenschaften hat, und nach der Messung wieder herein, es ist immer real vorhanden, es wechselt auch nicht seinen Zustand (wie soll das gehen) oder "ergreift" eine Eigenschaft oder rast als unvollständiges Eigenschaftsbündel durch die Apparatur. Es ist eben immer das, was es ist, nur hat es eine (wie ich es nenne ontologische) Unbestimmtheit, die eine Beschreibung nicht möglich macht, so wie man ein unbekanntes Objekt, das im Dunkel ist, nicht sagen kann, ob es rund oder eckig ist, obwohl es irgendwie sein muss.
Bitte verstehe mich, es kommt mir nicht darauf an, mit meinen Interpretationen Recht zu haben, ich führe diese deshalb auf, weil es sich im Diskurs gehört, seine Argumentation zu begründen (hier die über die Unbestimmtheit). Leider macht das bei der Präzisierung der von Physikern meistens sehr pragmatisch verwendeten Begriffe viele Umstände.
Grüße Bernd |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 11. Mai 2020 21:24 Titel: Bernd Stein Verfasst am: 11. Mai 2020 21:24 Titel: |
 |
|
Hi,
langer Rede kurzer Sinn: vor einer Wechselwirkung mit einem Messgerät hat ein Quantenobjekt immer noch zu viele Freiheiten oder Möglichkeiten, zu sein oder zu wirken, was mich daran hindert, sein Verhalten und seine Beschaffenheit eindeutig beschreiben zu können.
Das ist die Antwort auf Deine Frage.
Grüße |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 11. Mai 2020 21:30 Titel: Bernd Stein Verfasst am: 11. Mai 2020 21:30 Titel: |
 |
|
Hi Tom
von epistemischer Unbestimmtheit war nie die Rede- im Gegenteil, diese hatte ich ausgeschlossen. Ich hatte den ontologischen Aspekt des von mit verwendeten Unbestimmtheitsbegriffs mehrfach betont.
Grüße
Bernd. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Mai 2020 07:39 Titel: index_razor Verfasst am: 12. Mai 2020 07:39 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Hi,
langer Rede kurzer Sinn: vor einer Wechselwirkung mit einem Messgerät hat ein Quantenobjekt immer noch zu viele Freiheiten oder Möglichkeiten, zu sein oder zu wirken, was mich daran hindert, sein Verhalten und seine Beschaffenheit eindeutig beschreiben zu können.
Das ist die Antwort auf Deine Frage.
|
Ich wollte von dir wissen, warum du den einen konkreten Ort
 = \int\dd^3 x\ \vec{x} |\psi(\vec{x},t)|^2 )
und den einen konkreten Impuls
 = -i\hbar\int \dd^3 x\ \psi^\star(\vec{x},t)\nabla \psi(\vec{x},t),)
die ich direkt aus der Lösung der Schrödingergleichung und Observablenalgebra abgeleitet habe, nicht als objektive Eigenschaften des Quantensystems ansehen willst. Das ist eigentlich erstmal alles, was mich interessiert, und das hast du nun wieder mit keiner Silbe beantwortet. Stattdessen betest du nur wieder deine Überzeugung herunter, daß aus dem Formalismus keine solche Eigenschaften ableitbar sind.
| Zitat: |
Ein Meßvorgang wird aber von der SG und der Algebra nicht beschrieben.
|
Und wie kommst du darauf? Eine Messung ist mit ziemlicher Sicherheit nichts anderes als eine Wechselwirkung zwischen zwei Quantensystemen, von denen eines makroskopisch ist. Diese Wechselwirkung beschreibt die Quantenmechanik prinzipiell mit einem Element aus ihrer Observablenalgebra.
Den Zeitpunkt jedes einzelnen Klicks in einem Detektor wird dir natürlich niemand vorhersagen können. Allerdings garantiert dir auch niemand, daß jeder einzelne dieser Klicks eine objektive Eigenschaft des Systems repräsentiert. Das wäre wiederum nur deine Interpretation des Meßvorgangs. |
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
 Qubit Verfasst am: 12. Mai 2020 09:23 Titel: Qubit Verfasst am: 12. Mai 2020 09:23 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Ich wollte von dir wissen, warum du den einen konkreten Ort
 = \int\dd^3 x\ \vec{x} |\psi(\vec{x},t)|^2 )
und den einen konkreten Impuls
 = -i\hbar\int \dd^3 x\ \psi^\star(\vec{x},t)\nabla \psi(\vec{x},t),)
die ich direkt aus der Lösung der Schrödingergleichung und Observablenalgebra abgeleitet habe, nicht als objektive Eigenschaften des Quantensystems ansehen willst.
|
Die Erwartungswerte von Ort/Impuls als "objektive Eigenschaften des Quantensystems" zu betrachten, ist so sinnig, wie den Erwartungswert 3.5 der "Eigenzustände" 1-6 eines Würfels als Eigenschaft des Würfels zu betrachten, gar nicht. Erwartungswerte sagen etwas über statistische Gesamtheiten aus, erst dann machen sie Sinn.
| Zitat: |
Eine Messung ist mit ziemlicher Sicherheit nichts anderes als eine Wechselwirkung zwischen zwei Quantensystemen, von denen eines makroskopisch ist. Diese Wechselwirkung beschreibt die Quantenmechanik prinzipiell mit einem Element aus ihrer Observablenalgebra.
Den Zeitpunkt jedes einzelnen Klicks in einem Detektor wird dir natürlich niemand vorhersagen können. Allerdings garantiert dir auch niemand, daß jeder einzelne dieser Klicks eine objektive Eigenschaft des Systems repräsentiert. Das wäre wiederum nur deine Interpretation des Meßvorgangs. |
Es gibt keine QFT der quantenmechanischen Messungen, oder? Die einzige konsistente Beschreibungen mit Messungen sind Eigenwerte der Observablen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 12. Mai 2020 10:21 Titel: TomS Verfasst am: 12. Mai 2020 10:21 Titel: |
 |
|
| Qubit hat Folgendes geschrieben: |
Die Erwartungswerte von Ort/Impuls als "objektive Eigenschaften des Quantensystems" zu betrachten, ist so sinnig, wie den Erwartungswert 3.5 der "Eigenzustände" 1-6 eines Würfels als Eigenschaft des Würfels zu betrachten, gar nicht. Erwartungswerte sagen etwas über statistische Gesamtheiten aus, erst dann machen sie Sinn. |
Einwand, euer Ehren.
Deine Argumentation gilt erst dann, wenn du die Wellenfunktion bzw. den Zustand nicht als Beschreibung eines einzelnen Objektes bzw. Quantensystems interpretierst, sondern als Eigenschaft eines Ensembles. Das ist hier jedoch nicht gegeben.
Die Mathematik macht keinen Unterschied zwischen den beiden Zahlen "k" in
 | \psi_k\rangle = 0)

Du machst den Unterschied, wenn du ersteres als einen Eigenzustand eines Quantensystems und damit "k" als Eigenschaft dieses einen Systems betrachtest, jedoch letzteres als Eigenschaft eines Ensembles.
Wenn du die Quantenmechanik so auffasst, dass ein Zustand ein Quantensystems repräsentiert - nicht ein Ensemble - dann ist auch die zweite eine Beschreibung einer Eigenschaft dieses einen Quantensystems, denn du kannst sie aus dem Zustandsvektor dieses Quantensystems herauspräparieren.
Dass du anhand eines Ensemble nachprüfen bzw. messen musst, kommt erst später ins Spiel.
Neben vielen anderen Begriffsverwirrungen in diesem Thread stört auch die fehlende Definition, auf was sich der Zustandsvektor bezieht und was mit "Eigenschaft" gemeint ist. Evtl. wird hier implizit "klassische Eigenschaft" verstanden; das ist natürlich ein ungerechtfertigtes Vorurteil.
Wenn der Zustandsvektor ein einzelnes System im ontischen Sinne beschreibt, dann ist genau dieser Zustandsvektor die wesentliche Eigenschaft des Systems - bezogen auf die durch die Observablenalgebra feiner definierte Geometrie des Hilbertraumes.
Genauso ist der Ortsvektor eines klassischen Systems auf einer Kugeloberfläche eine wesentliche Eigenschaft des Systems - bezogen auf die durch die ein Koordinatensystem oder reale Orte feiner definierte Geometrie der Kugeloberfläche. Wenn ich sage, Gegeben sei ein Ort (theta, phi), dann ist das für sich alleine sinnlos; wenn theta und phi jedoch bzgl. Nordpol, Südpol und Greenwich gegeben sind, dann weiß ich, um welchen Ort es sich tatsächlich handelt.
In völlig analoger Weise liefert der quantenmechanische Zustandsvektor eine ausrechende Beschreibung, wenn ich ihn im Kontext der physikalisch relevanten Observablenalgebra verstehe, d.h. seine Projektionen auf die Eigenzustände der Observablen kenne, also (theta, phi, ...)
Und genauso bleibt beides unspezifiziert, wenn ich den Kontext nicht nenne, wenn ich also weder den Bezugspunkt Greenwich usw. angebe, oder es versäume, klarzustellen, dass es sich um eine Punkt auf dem Saturn handelt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 12. Mai 2020 11:34, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Mai 2020 10:24 Titel: index_razor Verfasst am: 12. Mai 2020 10:24 Titel: |
 |
|
| Qubit hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ich wollte von dir wissen, warum du den einen konkreten Ort
 = \int\dd^3 x\ \vec{x} |\psi(\vec{x},t)|^2 )
und den einen konkreten Impuls
 = -i\hbar\int \dd^3 x\ \psi^\star(\vec{x},t)\nabla \psi(\vec{x},t),)
die ich direkt aus der Lösung der Schrödingergleichung und Observablenalgebra abgeleitet habe, nicht als objektive Eigenschaften des Quantensystems ansehen willst.
|
Die Erwartungswerte von Ort/Impuls als "objektive Eigenschaften des Quantensystems" zu betrachten, ist so sinnig, wie den Erwartungswert 3.5 der "Eigenzustände" 1-6 eines Würfels als Eigenschaft des Würfels zu betrachten, gar nicht. Erwartungswerte sagen etwas über statistische Gesamtheiten aus, erst dann machen sie Sinn.
|
Es zwingt dich aber niemand, diese beiden Größen als Erwartungswerte einer statistischen Gesamtheit zu interpretieren. Das ist doch gerade mein Punkt. Die Bornsche Regel wird so selten hinterfragt, daß anscheinend gern vergessen wird, daß sie nicht zum formalen Kern der Quantenmechanik gehört.
| Zitat: |
| Zitat: |
Eine Messung ist mit ziemlicher Sicherheit nichts anderes als eine Wechselwirkung zwischen zwei Quantensystemen, von denen eines makroskopisch ist. Diese Wechselwirkung beschreibt die Quantenmechanik prinzipiell mit einem Element aus ihrer Observablenalgebra.
Den Zeitpunkt jedes einzelnen Klicks in einem Detektor wird dir natürlich niemand vorhersagen können. Allerdings garantiert dir auch niemand, daß jeder einzelne dieser Klicks eine objektive Eigenschaft des Systems repräsentiert. Das wäre wiederum nur deine Interpretation des Meßvorgangs. |
Es gibt keine QFT der quantenmechanischen Messungen, oder? Die einzige konsistente Beschreibungen mit Messungen sind Eigenwerte der Observablen. |
Wir brauchen auch keine QFT extra für Messungen. Ein Meßgerät besteht aus derselben Materie, die das Standardmodell beschreibt. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Mai 2020 12:19 Titel: index_razor Verfasst am: 12. Mai 2020 12:19 Titel: |
 |
|
| Qubit hat Folgendes geschrieben: |
Die Erwartungswerte von Ort/Impuls als "objektive Eigenschaften des Quantensystems" zu betrachten, ist so sinnig, wie den Erwartungswert 3.5 der "Eigenzustände" 1-6 eines Würfels als Eigenschaft des Würfels zu betrachten, gar nicht. Erwartungswerte sagen etwas über statistische Gesamtheiten aus, erst dann machen sie Sinn.
|
Übrigens, weil es grad so schön zum Thema paßt, vielleicht noch eine Literaturempfehlung:
"On the level of the theory, probability and statistics play no role at all -- not even in quantum statistical mechanics, where only the basic intuition is colored by statistical ideas. Probability and statistics make their appearance only when discussing the interface between theory and experiment, where their use is dictated by handling noisy open systems using multiple measurements and the law of large numbers. This is in complete agreement with how probability and statistics appear in classical physics.
This strongly suggests that q-expectations should be regarded as objective properties of quantum systems, [...] even in situations where there are seeming discrepancies, such as in experiments involving a multitude of single, experimentally distinguishable events."
Arnold Neumaier, Coherent Quantum Physics -- A Reinterpretation of the Tradition.
Ich möchte behaupten, daß jeder, der sich für Interpretationsfragen der Quantenmechanik interessiert, sich zumindest mal anhören sollte, was Arnold Neumaier zu dem Thema zu sagen hat. Meines Erachtens ist viel aufschlußreiches darunter. Der Inhalt des oben zitierten Buches kann auch zum Großteil einer Serie von Preprints auf arxiv entnommen werden (links auf der Homepage des Autors). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 12. Mai 2020 13:25 Titel: TomS Verfasst am: 12. Mai 2020 13:25 Titel: |
 |
|
alles sehr bedenkenswerte Punkte, die index_razor da vorbringt
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
 Qubit Verfasst am: 12. Mai 2020 14:59 Titel: Qubit Verfasst am: 12. Mai 2020 14:59 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | alles sehr bedenkenswerte Punkte, die index_razor da vorbringt |
Interessante mathematische Darstellung eines Mathematikers.
Für die Physik sehe ich hier aber vorerst nur empirisch relevant..
| Zitat: | 3.6 ..
We now show that a q-expectation, though introduced as an intrinsic measure of
uncertainty, may be viewed as a statistical property of many independent identically prepared systems. We regard the systems of the population considered as subsystems of a bigger system
|
Es ist sicher verlockend, Ehrenfest zu einem umfassenden Prinzip zu erheben:
}{dx} \Big >)
Für mich bleibt das aber ein Korrespondenzprinzip, die eigentlich Physik erfolgt "innerhalb der spitzen Klammern".
Aber ich kenne die angesprochene Interpretation zu wenig. Was ist denn da die "reinterpretierte" Bedeutung der Wellenfunktion? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Mai 2020 16:01 Titel: index_razor Verfasst am: 12. Mai 2020 16:01 Titel: |
 |
|
| Qubit hat Folgendes geschrieben: |
Interessante mathematische Darstellung eines Mathematikers.
Für die Physik sehe ich hier aber vorerst nur empirisch relevant..
| Zitat: | 3.6 ..
We now show that a q-expectation, though introduced as an intrinsic measure of
uncertainty, may be viewed as a statistical property of many independent identically prepared systems. We regard the systems of the population considered as subsystems of a bigger system
|
|
Warum soll nur das empirisch relevant sein? Empirisch relevant ist jegliche Korrelation zwischen den makroskopischen q-Observablen (kleine Unsicherheit) des Detektors und den q-Observablen des Systems. Wenn der zu messende q-Erwartungswert hinreichend signifikant (rauschfrei) ist, ist Statistik irrelevant. Wenn nicht, wird sie notwendig um ein signifikantes Ensemblemittel zu bilden. Das ist nicht anders als in der klassischen Physik.
| Zitat: |
Es ist sicher verlockend, Ehrenfest zu einem umfassenden Prinzip zu erheben:
}{dx} \Big >)
Für mich bleibt das aber ein Korrespondenzprinzip, die eigentlich Physik erfolgt "innerhalb der spitzen Klammern".
|
Das ergibt keinen Sinn. Innerhalb der spitzen Klammern steht nur die Definition der jeweiligen dynamischen Größen aus dem mathematischen Formalismus der Theorie, für den es verschiedene äquivalente Formulierungen gibt. Was ist daran "die eigentliche Physik"?
Das Ehrenfestsche Theorem ist allgemeingültig und gilt nicht nur im klassischen Grenzwert. Man muß es also zu gar nichts "erheben". Das hat doch nichts mit einem Korrespondenzprinzip zu tun.
| Zitat: |
Aber ich kenne die angesprochene Interpretation zu wenig. Was ist denn da die "reinterpretierte" Bedeutung der Wellenfunktion? |
Die Wellenfunktion, bzw. allgemeiner der statistische Operator, ist der Zustand eines einzelnen Quantensystems, nicht einer statistischen Gesamtheit. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 13. Mai 2020 14:58 Titel: Bernd Stein Verfasst am: 13. Mai 2020 14:58 Titel: |
 |
|
Hi Index razor,
Du hast die ganze Zeit von einer Gesamtheit einzelner Quantenobjekte geredet, was ich nicht gesehen habe. Ich habe nur von einem einzelnen Quantenobjekt geredet. Behauptest Du, der Erwartungswert, der Mittelwert aus Messungen an vielen Einzelobjekten, ist sei eine reale Eigenschaft des Ensembles ? oder sogar der einzelnen Systems ?
Den Einzelobjekten werden durch Messung individuelle Eigenschaften zugeordnet, das dürfte unstrittig sein.
Zum Beispiel ein definierter Ort. Aus vielen gemessenen Orten kann ich einen zentralen Ort bilden, und sagen dieses Zentrum ordne ich dem Ensemble nach der Messung zu. Das ist soweit verständlich.
Dass man einem Ensemble oder einem Einzelteilchen durch Messung (mein Jagron: Wegnahme von Unbestimtheiten) eine Bestimmtheit geben kann, habe ich auch immer behauptet.
Es geht mir aber um die Frage, was ist v o r der Messung (oder anders gesagt, unabhängig von einer Beobachtung). Was für einen Ort hat das Ensemble vor der Messung ? Welchen Ort hat das einzelne Quantenobjekt vor der Messung. Was sagt der mathematische Apparat über den Ort v o r der Messung aus ?
Wenn er nichts bestimmtes sagt,
a) wie definierst Du dann die dem Objekt zukommende Unbestimmtheit, und
b) woher rührt diese Unbestimmtheit ?
Ist es eine intrinsiche, oder relationale oder strukturelle oder epistemische oder ontologische oder eine, über die es keinen Begriff gibt, oder so einen wie den des "Überlagerungsszustandes" ? Wenn der Apparat etwas sagt, was zu interpretieren ist, dann wäre ich an Deiner Interpretation interessiert.
Du kannst gerne ein Ensemble aus Spin ½ Teilchen als Beispiel nehmen. Den Einzelobjekten wird durch Messung längs einer Achse ein individueller Spin zugewiesen (+-1/2). Aus vielen Spinmessungen kann ich einen Mittelwert bilden ? Wie soll dieser aussehen? Was ist vor der Messung ? Welche Unbestimmtheit ?
Ich frage auch deshalb, weil ich anschließend gerne wüßte, worin Du den Unterschied siehst zwischen den Unbestimmtheiten, die einem klassischen Objekt zukommen, dessen Zustand mathematisch durch den klassischen Phasenraum beschrieben werden , und den Unbestimmtheiten eines qm Objekts, dessen Zustand durch Vektoren oder Funktionen eines Hilbertraumes beschrieben werden.
Grüße
Bernd |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 13. Mai 2020 17:20 Titel: TomS Verfasst am: 13. Mai 2020 17:20 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | | ... weil ich ... gerne wüßte, worin Du den Unterschied siehst zwischen den Unbestimmtheiten, die einem klassischen Objekt zukommen, dessen Zustand mathematisch durch den klassischen Phasenraum beschrieben werden, und den Unbestimmtheiten eines qm Objekts, dessen Zustand durch Vektoren oder Funktionen eines Hilbertraumes beschrieben werden. |
Auf dieser Ebene kommt dem quantenmechanischen Systeme keine Unbestimmtheit zu, denn der Zustandsvektor im Hilbertraum ist scharf definiert.
Die Unbestimmtheit kommt erst dann ins Spiel, wenn du feststellst, dass ein Zustand nicht gleichzeitig ein Eigenzustand zu zwei nicht-kommutierenden Observablen sein kann. Aber das erkennst du erst, wenn du die Rolle der Observablen klärst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 13. Mai 2020 17:50 Titel: index_razor Verfasst am: 13. Mai 2020 17:50 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: |
Du hast die ganze Zeit von einer Gesamtheit einzelner Quantenobjekte geredet, was ich nicht gesehen habe. Ich habe nur von einem einzelnen Quantenobjekt geredet. Behauptest Du, der Erwartungswert, der Mittelwert aus Messungen an vielen Einzelobjekten, ist sei eine reale Eigenschaft des Ensembles ? oder sogar der einzelnen Systems ?
|
Ich habe nie von statistischen Gesamtheiten gesprochen. Das war Qubit. Ich habe sogar am Anfang gesagt, daß ich mich zum Zwecke der Diskussion von der statistischen Interpretation des Formalismus distanzieren will. Auch mir ging es um die Frage, ob der Formalismus eine Interpretation für individuelle Systeme erlaubt.
| Zitat: |
Es geht mir aber um die Frage, was ist v o r der Messung (oder anders gesagt, unabhängig von einer Beobachtung).
|
Das mußt du mir nicht jedes mal wieder erklären. Das habe ich längst verstanden.
| Zitat: |
Was für einen Ort hat das Ensemble vor der Messung ?
|
Ein Ensemble hat keinen Ort, sondern bestenfalls einen Ortserwartungswert, der statistischer Art ist.
| Zitat: |
Welchen Ort hat das einzelne Quantenobjekt vor der Messung. Was sagt der mathematische Apparat über den Ort v o r der Messung aus ?
|
Das beantworte ich jetzt mindestens zum dritten mal:
 = \int \dd^3 x\ \vec{x}|\psi(\vec{x}, t)|^2.)
Zumindest halte ich das für eine mögliche Interpretation des Ortes eines einzelnen Quantenobjekts. Es wäre hilfreich, wenn du diese Antwort jetzt mal zur Kenntnis nimmst und gegebenenfalls klar machst, was du dagegen für Einwände hast.
Dieser Ort besitzt allerdings eine intrinsische Unsicherheit, gegeben durch die quantenmechanische Ortsunschärfe ("q-uncertainty"). Das bedeutet aber nicht, daß es sich bei ) nicht um eine objektive Eigenschaft eines Individuums handeln kann. Im Gegenteil, die Unbestimmtheit des Ortes kann eine weitere objektive Eigenschaft eines individuellen Systems sein. Mehr dazu gleich. nicht um eine objektive Eigenschaft eines Individuums handeln kann. Im Gegenteil, die Unbestimmtheit des Ortes kann eine weitere objektive Eigenschaft eines individuellen Systems sein. Mehr dazu gleich.
| Zitat: |
Wenn er nichts bestimmtes sagt,
a) wie definierst Du dann die dem Objekt zukommende Unbestimmtheit, und
|
Wir sollten wohl mal ein terminologisches Problem klären. Daß eine Eigenschaft eine "Unbestimmtheit" oder besser, Unsicherheit, besitzt, bedeutet nicht, daß man überhaupt "nichts bestimmtes über sie aussagen kann". Sofern ich diese Unbestimmtheit quantifizieren kann, hindert mich nichts an konkreten Aussagen über Einzelsysteme.
| Zitat: |
b) woher rührt diese Unbestimmtheit ?
|
Diese Unbestimmtheit resultiert sowohl aus der Definition der betreffenden Größe als auch aus dem Zustand des Systems.
Beispiel: Laut Wikipedia befindet sich Berlin am Ort: 52°31′12″N 13°24′18″E. Obwohl eine Winkelsekunde meines Wissens ca. 20-30 m sind, ist diese Angabe sicher nur bis auf einige 10 Kilometer genau. Woher kommt diese Unsicherheit? Liegt Berlin mal hier und mal dort? Oder gibt es gar ein ganzes Ensemble von Berlins mit individuell verschiedenen Orten? Keineswegs. Der "Ort" von Berlin besitzt einfach eine intrinsische Unsicherheit, und zwar deshalb, weil Berlin nicht punktförmig ist. Trotzdem sagen wir nicht, daß Berlin objektiv keinen Ort hat. Der Ort ist eben mit einer prinzipiellen Unsicherheit versehen, die nicht statistischen Ursprungs ist.
| Zitat: |
Ist es eine intrinsiche, oder relationale oder strukturelle oder epistemische oder ontologische oder eine, über die es keinen Begriff gibt, oder so einen wie den des "Überlagerungsszustandes" ? Wenn der Apparat etwas sagt, was zu interpretieren ist, dann wäre ich an Deiner Interpretation interessiert.
|
Als "intrinsisch" habe ich die Unsicherheit ja oben selbst bezeichnet. Allerdings ist das natürlich nur ein Füllwort ohne präzise Bedeutung. Orte von individuellen Quantensystemen sind -- ungefähr so, wie der von Berlin -- eben einfach prinzipiell unsicher. (Mit Ausnahme von Fällen, die man ohnehin als theoretische Idealisierung betrachten muß.)
| Zitat: |
Du kannst gerne ein Ensemble aus Spin ½ Teilchen als Beispiel nehmen. Den Einzelobjekten wird durch Messung längs einer Achse ein individueller Spin zugewiesen (+-1/2). Aus vielen Spinmessungen kann ich einen Mittelwert bilden ? Wie soll dieser aussehen? Was ist vor der Messung ? Welche Unbestimmtheit ?
|
Ehrlich gesagt verstehe ich die Relevanz dieser Fragen nicht so ganz. Du kannst natürlich aus beliebig vielen Messungen einen Mittelwert bilden. Je mehr unabhängige Messungen du durchführst, desto signifikanter wird der Mittelwert, d.h. seine Unsicherheit sinkt, typischerweise mit  , wobei N die Anzahl der Messungen ist. , wobei N die Anzahl der Messungen ist.
Dieser Mittelwert ist für beliebiges N eine Approximation für einen festen dreidimensionalen Vektor, der den objektiven eindeutigen Spin des Objekts charakterisiert.
| Zitat: |
Ich frage auch deshalb, weil ich anschließend gerne wüßte, worin Du den Unterschied siehst zwischen den Unbestimmtheiten, die einem klassischen Objekt zukommen, dessen Zustand mathematisch durch den klassischen Phasenraum beschrieben werden , und den Unbestimmtheiten eines qm Objekts, dessen Zustand durch Vektoren oder Funktionen eines Hilbertraumes beschrieben werden.
|
In der klassischen Theorie tauchen Unbestimmtheiten der dynamischen Größen nur in der statistischen Thermodynamik auf. In der Quantenmechanik tauchen sie in jedem Zustand auf.
Zuletzt bearbeitet von index_razor am 13. Mai 2020 18:57, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 13. Mai 2020 18:20 Titel: TomS Verfasst am: 13. Mai 2020 18:20 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | In der klassischen Theorie tauchen Unbestimmtheiten der dynamischen Größennur in der statistischen Thermodynamik auf. In der Quantenmechanik tauchen sie in jedem Zustand auf. |
@Bernhard:
Das ist ein wichtiger Punkt:
In der QM liegt eine Unbestimmtheit der dynamischen Größen in einem Zustand vor, nicht jedoch eine Unbestimmtheit des Zustandes selbst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 13. Mai 2020 19:05 Titel: index_razor Verfasst am: 13. Mai 2020 19:05 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
In der QM liegt eine Unbestimmtheit der dynamischen Größen in einem Zustand vor, nicht jedoch eine Unbestimmtheit des Zustandes selbst. |
Allerdings. Vielleicht sollte ich im Hinblick darauf obige Aussage von mir noch klarstellen:
| index_razor hat Folgendes geschrieben: |
Diese Unbestimmtheit resultiert sowohl aus der Definition der betreffenden Größe als auch aus dem Zustand des Systems.
|
Damit wollte ich nur sagen, daß die Unbestimmtheit von X auch vom Zustand abhängt, nicht daß der Zustand unbestimmt ist. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 13. Mai 2020 23:51 Titel: Bernd Stein Verfasst am: 13. Mai 2020 23:51 Titel: |
 |
|
Hi index razor,
1) ich lese wirklich zum dritten Mal, dass Du den Ortserwartungswert einer Vielzahl von Messungen als Ort eines einzelnen Quantenobjektes auffasst, was mir jedes Mal intuitiv widersinnig erschienen ist, sorry, dass ich deine Ausführungen ignoriert habe. Nun schränkst Du diese Behauptung allerdings etwas ein, indem Du sagst, dass man den Erwartungswert auch so „interpretieren“ könnte.
Das denke, das ist nicht richtig. Hier meine Begründung:
a) Zum Zeitpunkt der Messung:
Wenn ich den Ort eines Einzelobjektes messe, erhalte ich einen definierten Ort (ohne Unschärfe, ohne Unbestimmtheiten, einen „scharfen“ Ort). Messe ich dann den Ort vieler gleichartiger oder gleich präparierter Objekte, erhalte ich ebenfalls wieder jeweils scharfe Orte, nur streuen die Ortswerte dann. Der Erwartungswert der Ortsmessungen ist aber ein anderer als der scharf gemessene Ort des ersten Objektes, folglich kann der Ort dieses Objektes (und der der anderen auch) zum Zeitpunkt der Messung nicht der Ortserwartungswert sein.
Was sagt der algebraische Apparat? Er sagt den Ortserwartungswert als Messergebnis vorher.
Nur ist der „scharfe“ Ortserwartungswert für eine Vielzahl von Messungen u n g l e i c h dem scharfen Ortswert einer Einzelmessung.
Was ist der Erwartungswert von Spinmessungen einer Vielzahl von Spin-1/2-Teilchen, meiner Meinung nach müßte dieser Null sein, ein Einzelobjekt hat aber den Spin +-1/2. Erwartungswert und Einzelwert sind auch hier nicht gleich.
Alle Orte jeweils bezogen auf den Zeitpunkt der Messung !
b) Zeitpunkte vor der Messung:
Der Ort eines Einzelobjektes ist unbestimmt, weil der algebraische Apparat dazu nichts sagt. Der algebraische Apparat sagt nur einen Mittelwert von Ortmessergebnissen vorher, und zwar nicht, weil ich die Algebra instrumentalistisch interpretiere, sondern weil sie dies faktisch so tut. Es lässt sich nichts anderes aus der Mathematik herauslesen. Der algebraische Apparat macht keine Vorhersage über den Ort vor der Messung. Die Algebra kennt das Wort „Ort“ vor einer Messung schlichtweg nicht, und kann deshalb darüber nichts sagen, das ist der schlichte Grund. Gemeint ist natürlich immer ein bestimmter Ort.
Die Algebra sagt aber auch nichts über einen „unscharfen“ Ort vor der Messung, wenn sie das Wort „Ort“ nicht zur Verfügung hat. Eine Gleichung, die eine raumgreifende Welle beschreibt, kann uns nicht sagen, wo sich die Welle befindet, weil das Wort Ort in ihrem Sprachschatz nicht vorkommt.
Warum ist das bei einem einzelnen Quantenobjekt so? Ich denke, weil das Objekt v o r der Messung i m m e r mehrere Möglichkeiten für einen Ort „hat“. Wir können auch aus keinem sonstigem Meßergebnis auf den Ort schlußfolgern, er ist induktiv nicht erschließbar, insofern ist der Ort „ontologisch“ unbestimmt. Schon bei zwei gleichzeitig vorhandenen Möglichkeiten für einen Ort kannst Du keinen bestimmten Ort mehr angeben, es ist sinnlos, von einem bestimmten Ort des Objektes zu sprechen. Du kannst von einem möglichen Ort sprechen, einem potentiellen, einem gedachten, aber all diese Propositionen stiften Unbestimmtheit (s. unten) durch Hinzufügung eines Prädikats, das vom Subjekt nicht zu trenne ist, also epistemische Unbestimmtheiten. Hier handelt es sich aber nicht um epistemische Unbestimmtheiten, weil es zwar das Wort „Ort“ und bestimmte Prädikate gibt, aber keine Zuordnung von Ort und Objekt, auf die es ankommt. Ich bin auch anders als Du der Meinung, dass der Ort keine intrinsiche Eigenschaft ist, die dem Objekt von sich aus zukommt, sondern eine extrinsische, ein Ort ist immer dem Objekt von den außeren Bedingungen „aufgeprägt“, das Objekt ist immer an einem Ort auf Grund äußerer Zwänge, genauso ist es mit der Energie, der Impuls und Drehimpuls eines Objektes, alles hängt zum Beispiel vom Koordinatenursprung ab und vom Bewegungszustand, der Ort ist nicht lorenz oder sonstwie invariant.
2) Nun sagt Du, dass die Unbestimmtheit des Ortes auch eine weitere objektive Eigenschaft eines individuellen Systems sein kann. Unbestimmtheit als objektive Eigenschaft ? Physikalische Eigenschaft ? Meinst Du die Heisenbergsche Ortsunschärfe ? Das ist eine Unbestimmtheit wegen Streuung von Messergebnissen, keine intrinsische Unschärfe. Ein Objekt ist immer genau so scharf an einem Ort, wie die lokale Wirkung scharf ist, die seinen Ort beobachtbar macht. Ein Objekt hat ja nur deshalb einen Ort, weil an diesem Ort eine lokale Wirkung stattfindet, Ort ist immer Ort einer Wirkung. Eine andere Ortszuweisung auf gedanklicher, abstrakter, modellhafter Ebene kannst Du auch machen, das ist aber eine Idealisierung, und die hat in jedem Fall immer die Unschärfe NULL. Also wenn Du den Ort eines Modell- sondern Realobjektes beschreiben willst, sind dessen Koordinaten so unscharf wie seine lokale spezifische WW unscharf ist.
Deinen Unbestimmtheitsbegriff als „Unschärfe“ eines Einzelteilchens verstehe ich daher nicht. Nach all dem bin ich der Meinung, dass man tatsächlich den Eigenschaftsbegriff möglichst vermeiden sollte, weil dieser in seinen verschiedenen Bedeutungen bei der Interpretation der qm Theorie nur Verwirrung stiftet. Ein Quantenobjekt kann seine Identität auch durch etwas anderes bekommen, aber dazu will ich im Moment nicht wieder ausholen.
3. Nun schreibst Du: „In der klassischen Theorie tauchen Unbestimmtheiten der dynamischen Größen nur in der statistischen Thermodynamik auf. In der Quantenmechanik tauchen sie in jedem Zustand auf.“ Ich interpretiere
das mit Ergänzung von Tom so, dass in der klassischen Physik (außer Thermodynamik) alle Meßgrößen aller Zustände zu allen Zeiten bestimmt sind, in der Quantenmechanik können die Meßgrößen eines Zustandes unbestimmt sein, seine Zustände sind immer bestimmt. Wie kann das sein, dass die Meßgrößen unbestimmt sind, der Zustand aber bestimmt? Ist das nur intuitiv gesagt, oder begründet, und was ist die Begründung für diesen Widerspruch ?
Ich würde dieser Behauptung zustimmen, aber nur, wenn Einigkeit herrscht über das, was mit „Bestimmtheit“ und „Unbestimmtheit“ gemeint ist. Es hilft alles nichts, um das zu begründen, muss an den Voraussetzungen angesetzt werden, die jeder Interpretation zugrunde liegen. Es geht ja nicht darum, wie ein Objekt nach unserer Vorstellung in der Realität beschaffen ist (wenn wir uns eine Vorstellung machen, haben wir die Interpretation schon durchgeführt). Es geht um die Interpretation der Mathematik als solcher. Was können wir als eine im Konsens verstandene Wahrheit aus der Symbolik der Mathematik als wahr herauslesen, darum geht es.
Anstelle der Toms´schen Axiomenliste, hier die die einfachere grundlegend angesprochene Thematik:
Woraus besteht die Mathematik einer jeden (!) physikalischen Theorie? Was kann sie im Prinzip aussagen?
Antwort: die Mathematik einer jeden (!) physikalischen Theorie besteht aus:
a) einer allgemeinen Gleichung, sollte so etwas wie eine „Gesamtheit“ beschreiben (z.B. von Phänomenen)
b) einer Algebra, diese beschreibt die Randbedingungen (die äußeren Einflüsse)
c) Bildet die Algebra ganz bestimmte Randbedingen in der Gleichung ab (Messsituation), kann aus der allgemeinen Gleichung im Verein mit der Algebra ein Meßwert vorhergesagt werden.
d) Eine Interpretation verwendet für operationale Zwecke (Zusammenfassungen, Vereinfachungen, zentrale Merkmale) geeignete Begriffe .
Sind wir darin einig, oder habe ich etwas dargestellt, was im Widerspruch zu etabliertem Wissen steht ?
Ich will erst man nicht weitergehen und warte auf Dein geschätzte Antwort.
Grüße Bernd |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 13. Mai 2020 23:56 Titel: Bernd Stein Verfasst am: 13. Mai 2020 23:56 Titel: |
 |
|
Bei allem, was ich vorstehend zum Beispiel bezgl. des Ortes eines Objektes behaupte, betrachte ich immer ein einzelnes Quantenobjekt, kein Ensemble !
Ich betrachte immer nur Einzeobjekte. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Mai 2020 07:50 Titel: index_razor Verfasst am: 14. Mai 2020 07:50 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Hi index razor,
1) ich lese wirklich zum dritten Mal, dass Du den Ortserwartungswert einer Vielzahl von Messungen als Ort eines einzelnen Quantenobjektes auffasst, was mir jedes Mal intuitiv widersinnig erschienen ist, sorry, dass ich deine Ausführungen ignoriert habe. Nun schränkst Du diese Behauptung allerdings etwas ein, indem Du sagst, dass man den Erwartungswert auch so „interpretieren“ könnte.
|
Deine Frage war was der mathematische Formalismus über den Ort aussagt. Antwort: Unter anderem  = \int\dd^3 x\ \vec{x}|\psi(\vec{x},t)|^2) . .
Daß es sich bei diesem  um den "Ortserwartungswert einer Vielzahl von Messungen" handelt, ist nur deine Interpretation auf Basis der Bornschen Regel, die nicht zum formalen, mathematischen Kern der Quantenmechanik gehört. um den "Ortserwartungswert einer Vielzahl von Messungen" handelt, ist nur deine Interpretation auf Basis der Bornschen Regel, die nicht zum formalen, mathematischen Kern der Quantenmechanik gehört.
Nur darum geht es. Du kannst von mir aus gern die ganze statistische Interpretation einfach weiterhin unhinterfragt übernehmen. Was du nicht kannst, ist, Behauptungen über den mathematischen Formalismus daraus ableiten.
| Zitat: |
Das denke, das ist nicht richtig. Hier meine Begründung:
a) Zum Zeitpunkt der Messung:
Wenn ich den Ort eines Einzelobjektes messe, erhalte ich einen definierten Ort (ohne Unschärfe, ohne Unbestimmtheiten, einen „scharfen“ Ort). Messe ich dann den Ort vieler gleichartiger oder gleich präparierter Objekte, erhalte ich ebenfalls wieder jeweils scharfe Orte, nur streuen die Ortswerte dann. Der Erwartungswert der Ortsmessungen ist aber ein anderer als der scharf gemessene Ort des ersten Objektes, folglich kann der Ort dieses Objektes (und der der anderen auch) zum Zeitpunkt der Messung nicht der Ortserwartungswert sein.
|
Das folgt deshalb nicht, weil es ebenso gut möglich ist, daß jede der Einzelmessung nicht genauer ist als  , die q-Unsicherheit des Ortes. , die q-Unsicherheit des Ortes.
| Zitat: |
Was sagt der algebraische Apparat? Er sagt den Ortserwartungswert als Messergebnis vorher.
|
Nein, tut er nicht. Der mathematische Apparat kennt den Begriff "Meßergebnis" überhaupt nicht.
| Zitat: |
Warum ist das bei einem einzelnen Quantenobjekt so? Ich denke, weil das Objekt v o r der Messung i m m e r mehrere Möglichkeiten für einen Ort „hat“. Wir können auch aus keinem sonstigem Meßergebnis auf den Ort schlußfolgern, er ist induktiv nicht erschließbar, insofern ist der Ort „ontologisch“ unbestimmt.
|
Hieran wird wieder offensichtlich, daß du die Behauptungen der orthodoxen Interpretation völlig unkritisch übernimmst und daraus falsche Aussagen über den "mathematischen Formalismus" extrapolierst. Nichts anderes versuche ich dir die ganze Zeit klar zu machen. Leider hast du das bis jetzt nicht mal im Ansatz erkannt.
| Zitat: |
2) Nun sagt Du, dass die Unbestimmtheit des Ortes auch eine weitere objektive Eigenschaft eines individuellen Systems sein kann. Unbestimmtheit als objektive Eigenschaft ? Physikalische Eigenschaft ? Meinst Du die Heisenbergsche Ortsunschärfe ?
|
Ja.
| Zitat: |
Das ist eine Unbestimmtheit wegen Streuung von Messergebnissen, keine intrinsische Unschärfe.
|
Wieder nur eine unkritsche Widerholung der statistischen Interpretation als "Gegenargument".
| Zitat: |
Deinen Unbestimmtheitsbegriff als „Unschärfe“ eines Einzelteilchens verstehe ich daher nicht.
|
Ich sage nur, es gibt Unsicherheiten, die nicht statistischen Ursprungs sind. Ich denke das ist offensichtlich (siehe "Ort" von Berlin). In diesem Sinne kann man auch die q-Unsicherheiten des QM-Formalismus interpretieren.
So, das reicht erst mal. Zum Rest vielleicht später.
Zuletzt bearbeitet von index_razor am 14. Mai 2020 12:47, insgesamt einmal bearbeitet |
|
 |
|
|















