| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18064
|
 TomS Verfasst am: 14. Mai 2020 08:47 Titel: TomS Verfasst am: 14. Mai 2020 08:47 Titel: |
 |
|
index_razor hat in allen essentiellen und nicht-essentiellen Punkten recht (das werden wir uns beide im Kalender anstreichen, das kommt selten vor). Leider verstehst du ihn aus irgendeinem Grund nicht, obwohl er das schon mehrfach klargestellt hat:
Es gibt
1) einen unstrittigen mathematischen Kern der Quantenmechanik - s.u.
2) Erweiterungen wie z.B. Projektionspostulat sowie
3) Interpretationen wie z.B. orthodox / Kopenhagen, Many Worlds, Ensemble, Thermal, ...
(3) fügt zu (2) im wesentlichen Begriffe hinzu; dazu gehört „Messung“, „Messwert“, „Erwartungswert für mehrere Messungen“, ... d.h. (2 + 3) gehören zusammen, jedoch ist (2) Mathematik und (Sprache).
Du solltest deine Beiträge daraufhin überprüfen: du sprichst sehr viel über (3) bzw. benutzt Begriffe aus (3), ohne dass du dir (1) wirklich klar gemacht hast, und ohne dass dir die Trennung zwischen (1) und (3) klar ist; außerdem fischst zu bzgl. (2) im Trüben, d.h. du möchtest eigentlich nur (1) betrachten, mischt jedoch immer irgendwas von (2 - Kopenhagen) mit rein, ohne dass dir das bewusst ist.
Hier nochmal zur Erinnerung:
Kursiv gesetzter Text bezieht sich auf reale Systeme und deren Dynamik, Präparation und Messung, sowie tatsächlich messbare Größen d.h. Observablen sowie deren Messwerte.
Normal gesetzter Text bezieht sich auf rein mathematische Objekte, die die o.g. physikalischen Systeme etc. in gewissem Sinne repräsentieren ².
Die folgenden Regeln sind identisch zu den etablierten Regeln ³ der 'orthodoxen Formulierung', jedoch ohne Betrachtung des Messprozesses.
1. Die Beschreibung eines Quantensystems erfolgt im Rahmen eines separablen Hilbertraumes 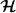
2. Der Zustand eines einzelnen ⁴ Quantensystems wird vollständig durch einen normierten Vektor ⁵ 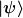 als Element dieses Hilbertraumes als Element dieses Hilbertraumes 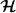 beschrieben. beschrieben.
3. Die Zeitentwicklung eines einzelnen isolierten ⁶ Quantensystems wird durch einen unitären Zeitentwicklungsoperator
 = e^{ -\mathrm{i}Ht })
mittels
\rangle = U(t)\,|\psi(0)\rangle)
beschrieben; 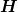 ist dabei der Hamiltonoperator. ist dabei der Hamiltonoperator.
Diese Regel ist vollständig äquivalent zur Schrödingergleichung ⁷
 \rangle = H \, |\psi(t) \rangle)
4. Eine beobachtbare Größe, d.h. eine Observable eines Quantensystems wird durch eine selbstadjungierten ⁸ Operator  repräsentiert, der auf die Zustandsvektoren repräsentiert, der auf die Zustandsvektoren 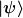 in in 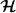 wirkt. wirkt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Mai 2020 17:57 Titel: index_razor Verfasst am: 14. Mai 2020 17:57 Titel: |
 |
|
Als Ergänzung zu meinem Beitrag https://www.physikerboard.de/ptopic,342993.html#342993
(bitte vorher lesen) noch ein paar Anmerkungen.
| Bernd Stein hat Folgendes geschrieben: |
b) Zeitpunkte vor der Messung:
Der Ort eines Einzelobjektes ist unbestimmt, weil der algebraische Apparat dazu nichts sagt. Der algebraische Apparat sagt nur einen Mittelwert von Ortmessergebnissen vorher, und zwar nicht, weil ich die Algebra instrumentalistisch interpretiere, sondern weil sie dies faktisch so tut. Es lässt sich nichts anderes aus der Mathematik herauslesen. Der algebraische Apparat macht keine Vorhersage über den Ort vor der Messung.
|
Der Fortschritt der Diskussion wird im Augenblick ungemein dadurch behindert, daß du meinst permanent Belehrungen über den "algebraischen Apparat", d.h. die Mathematik, der Quantenmechanik aussprechen zu müssen, von der du so gut wie gar nichts verstehst, wie du ja selbst schon zugegeben hast.
| Zitat: |
Die Algebra sagt aber auch nichts über einen „unscharfen“ Ort vor der Messung, wenn sie das Wort „Ort“ nicht zur Verfügung hat. Eine Gleichung, die eine raumgreifende Welle beschreibt, kann uns nicht sagen, wo sich die Welle befindet, weil das Wort Ort in ihrem Sprachschatz nicht vorkommt.
|
Meine Definition des Ortes ist auch keine Gleichung, "die eine raumgreifende Welle" beschreibt, sondern eine Gleichung, die einen Vektor, bzw. eine ganze Trajektorie im Raum beschreibt. So werden Orte und Bahnen von Objekten üblicherweise auch in der klassischen Theorie beschrieben.
| Zitat: |
Warum ist das bei einem einzelnen Quantenobjekt so? Ich denke, weil das Objekt v o r der Messung i m m e r mehrere Möglichkeiten für einen Ort „hat“. Wir können auch aus keinem sonstigem Meßergebnis auf den Ort schlußfolgern, er ist induktiv nicht erschließbar, insofern ist der Ort „ontologisch“ unbestimmt.
|
Lediglich für die Meßergebnisse gibt es mehrere Möglichkeiten. Das ist bei der Messung unsicherer Größen nichts besonderes. Die einzelnen Ergebnisse hängen eben nicht eindeutig von der objektiven Eigenschaft ab, die gemessen wird, sondern von zufälligen Einflüssen auf das Gesamtsystem aus Objekt und Detektor, die während der Messung stattfinden. Um diese quantitativ zu beschreiben, müßte man nicht nur den Zustand (die Wellenfunktion) des Objekts kennen, sondern den kompletten Meßprozeß modellieren. Da hieran normalerweise ein makroskopisches Objekt beteiligt ist, geht das nicht in beliebiger Detailstufe. Man kennt nur die Beschreibung offener Systeme mit Hilfe stochastischer Differentialgleichungen. Dies ist auch in der klassischen Theorie nicht wesentlich anders. Du kannst auch nicht jeden Einzelmeßwert für die Schwingungsdauer eines klassischen Pendels beliebig genau vorhersagen, obwohl das Pendel nach üblicher Interpretation nur eine Schwingungsdauer hat (sofern man alle seine objektiven Eigenschaften unverändert läßt).
| Zitat: |
Schon bei zwei gleichzeitig vorhandenen Möglichkeiten für einen Ort kannst Du keinen bestimmten Ort mehr angeben, es ist sinnlos, von einem bestimmten Ort des Objektes zu sprechen.
|
Das ist irrelevant. Es gibt nicht zwei Möglichkeiten für den Ort, sondern zwei Möglichkeiten für das Ergebnis einer Ortsmessung. Letztere Aussage ist als einzige wahrscheinlich unbestreitbar. Sie hängt aber sehr wohl davon ab, welche physikalischen Prozesse wir überhaupt geneigt sind als "Ortsmessung" gelten zu lassen. Das ist zum Teil Konvention, wie man nicht vergessen sollte. Wenn objektive Gründe dafür sprechen, daß ein bestimmter Prozeß für die mich interessierende Größe lediglich ein minimales Signal auf einem Berg von Rauschen produziert, dann bin ich irgendwann berechtigt diesen Prozeß nicht mehr als wirkliche "Messung" der Größe anzusehen. Wenn also ein Prozeß an identisch präparierten Systemen andauernd nur weit streuende Zufallswerte produziert, auf welcher Grundlage behauptest du dann, es handele sich um eine Messung einer bestimmten Größe?
| Zitat: |
Du kannst von einem möglichen Ort sprechen, einem potentiellen, einem gedachten, aber all diese Propositionen stiften Unbestimmtheit (s. unten) durch Hinzufügung eines Prädikats, das vom Subjekt nicht zu trenne ist, also epistemische Unbestimmtheiten. Hier handelt es sich aber nicht um epistemische Unbestimmtheiten, weil es zwar das Wort „Ort“ und bestimmte Prädikate gibt, aber keine Zuordnung von Ort und Objekt, auf die es ankommt.
|
Ich kann auch einfach von einem objektiv unsicheren Ort sprechen ohne irgendwelche Prädikate, die vom Subjekt nicht zu trennen sind. Daß ich dies tatsächlich kann, zeige ich durch eine entsprechende Interpretation des QM-Formalismus. Eine solche existiert (siehe meine obige Literaturempfehlung).
Damit sind alle deine Behauptungen darüber, was der "algebraische Apparat" angeblich faktisch nicht tut, hinfällig.
| Zitat: |
Ich bin auch anders als Du der Meinung, dass der Ort keine intrinsiche Eigenschaft ist, die dem Objekt von sich aus zukommt, sondern eine extrinsische, ein Ort ist immer dem Objekt von den außeren Bedingungen „aufgeprägt“, das Objekt ist immer an einem Ort auf Grund äußerer Zwänge, genauso ist es mit der Energie, der Impuls und Drehimpuls eines Objektes, alles hängt zum Beispiel vom Koordinatenursprung ab und vom Bewegungszustand, der Ort ist nicht lorenz oder sonstwie invariant.
|
Das hat doch mit dem Thema Quantenmechanik nichts mehr zu tun. Invariant ist dann eben der vektorielle Abstand zwischen 2 Objekten.
| Zitat: |
Nach all dem bin ich der Meinung, dass man tatsächlich den Eigenschaftsbegriff möglichst vermeiden sollte, weil dieser in seinen verschiedenen Bedeutungen bei der Interpretation der qm Theorie nur Verwirrung stiftet.
|
Es ist nicht zu leugnen, daß in dieser Diskussion einiges an Verwirrung besteht. Wovon diese verursacht ist, ist aber noch nicht vollkommen geklärt. Dein Urteil ist also voreilig.
| Zitat: |
3. Nun schreibst Du: „In der klassischen Theorie tauchen Unbestimmtheiten der dynamischen Größen nur in der statistischen Thermodynamik auf. In der Quantenmechanik tauchen sie in jedem Zustand auf.“ Ich interpretiere
das mit Ergänzung von Tom so, dass in der klassischen Physik (außer Thermodynamik) alle Meßgrößen aller Zustände zu allen Zeiten bestimmt sind, in der Quantenmechanik können die Meßgrößen eines Zustandes unbestimmt sein, seine Zustände sind immer bestimmt. Wie kann das sein, dass die Meßgrößen unbestimmt sind, der Zustand aber bestimmt? Ist das nur intuitiv gesagt, oder begründet, und was ist die Begründung für diesen Widerspruch ?
|
Natürlich läßt sich das begründen. Es liegt einfach daran, daß der q-Erwartungswert des Quadrats im allgemeinen ungleich dem Quadrat des q-Erwartungswertes ist, d.h.  . Das ist kein Widerspruch, sondern im Gegenteil eine unausweichliche Folge des mathematischen Formalismus der QM, sowie der statistischen Thermodynamik. . Das ist kein Widerspruch, sondern im Gegenteil eine unausweichliche Folge des mathematischen Formalismus der QM, sowie der statistischen Thermodynamik.
| Zitat: |
Ich würde dieser Behauptung zustimmen, aber nur, wenn Einigkeit herrscht über das, was mit „Bestimmtheit“ und „Unbestimmtheit“ gemeint ist. Es hilft alles nichts, um das zu begründen, muss an den Voraussetzungen angesetzt werden, die jeder Interpretation zugrunde liegen. |
Du bist gerade der einzige, der sich der impliziten Annahmen, die seine Schlußfolgerungen beeinflussen, nicht bewußt ist. Sonst würdest du im Rahmen des QM-Formalismus nicht dauernd von "Meßergebnissen" und deren "Erwartungswerten" reden, als sei dies das selbstverständlichste auf der Welt.
| Zitat: |
Es geht ja nicht darum, wie ein Objekt nach unserer Vorstellung in der Realität beschaffen ist (wenn wir uns eine Vorstellung machen, haben wir die Interpretation schon durchgeführt). Es geht um die Interpretation der Mathematik als solcher. Was können wir als eine im Konsens verstandene Wahrheit aus der Symbolik der Mathematik als wahr herauslesen, darum geht es. |
Ganz genau. Und wir können herauslesen, daß =\int\dd^3 x\ \vec{x}|\psi(x,t)|^2) der (unsichere) Ort eines individuellen Systems ist. der (unsichere) Ort eines individuellen Systems ist.
Wir können bekanntlich auch etwas anderes herauslesen. Es ist ja nichts neues, daß im Falle der QM verschiedene Interpretationen desselben Formalismus im Umlauf sind.
| Zitat: |
Woraus besteht die Mathematik einer jeden (!) physikalischen Theorie? Was kann sie im Prinzip aussagen?
Antwort: die Mathematik einer jeden (!) physikalischen Theorie besteht aus:
a) einer allgemeinen Gleichung, sollte so etwas wie eine „Gesamtheit“ beschreiben (z.B. von Phänomenen)
b) einer Algebra, diese beschreibt die Randbedingungen (die äußeren Einflüsse)
c) Bildet die Algebra ganz bestimmte Randbedingen in der Gleichung ab (Messsituation), kann aus der allgemeinen Gleichung im Verein mit der Algebra ein Meßwert vorhergesagt werden.
d) Eine Interpretation verwendet für operationale Zwecke (Zusammenfassungen, Vereinfachungen, zentrale Merkmale) geeignete Begriffe .
Sind wir darin einig, oder habe ich etwas dargestellt, was im Widerspruch zu etabliertem Wissen steht ?
|
Naja, a) und b) kann man so ungefähr gelten lassen, wenn das Wort "Algebra" nicht wäre, dessen Bedeutung du offenbar nicht richtig verstehst. Randbedingungen werden normalerweise nicht durch irgendwelche Algebren beschrieben. Algebren sind etwas, dessen Elemente man linear kombinieren und multiplizieren kann.
Punkte c) und d) sind sicher nicht allgemeingültig. Die Mathematik einer physikalischen Theorie beinhaltet normalerweise überhaupt keine spezifische Beschreibung für "Messungen" oder "Meßergebnisse". Die einzige Ausnahme ist hier die QM, die normalerweise so formuliert wird. Genau dieser Punkt führt dazu, daß so ein Interpretationswirrwarr besteht. Der Begriff "Messung" ist ja nirgendwo präzise definiert und taucht völlig isoliert in der Bornschen Regel und dem Kollapspostulat auf. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 14. Mai 2020 20:17 Titel: Bernd Stein Verfasst am: 14. Mai 2020 20:17 Titel: |
 |
|
Hi Index Razor,
die Bornsche Regel gehört nicht zur Algebra, sie ist aber Bestandteil der „Mathematik“ der Quantentheorie.
Ohne diese willkürliche Festlegung kommst Du nicht zu einer Messwertvorhersage – ohne diese Regel ist die ganze Mathematik der Quantentheorie zu nichts nutze. Wenn Du sagst, die gehöre nicht dazu, unterwühlst Du die grundsätzlich pragmatische Handhabung mathematischer Konzepte der Physik, auf denen sich ihr Erfolg gründet. Ich meine, das sollte alles keine Prinzipienfrage sein. Es kommt nicht darauf an.
Wichtiger ist: was meinst Du mit „(es kann sein), dass jede der Einzelmessung nicht genauer als die q-Unsicherheit des Ortes.“
Ich dachte es wäre unstrittig, dass bei einem Einzelobjekt ein Ort mit der Genauigkeit gemessen werden kann, mit die Wirkung lokal ist. Ist die Wirkung des Quantenobjektes, die Übertragung von Wirkungseinheiten, über einen kleinen Raumbereich verschmiert, zum Beispiel über lamda = h/p, dann messe ich einen kleinen verwaschenen Fleck, in einer kleinen Zeitspanne.
Wenn die q-Unsicherheit hinreichend groß ist, messe ich dann einen großen verwaschenen Fleck ? Ich denke Du hast eine q-Unsicherheit des Ortes v o r der Messung, aber nicht im Moment der Messung. Falls du eine intrinsische q-Unsicherheit des Ortes zum Zeitpunkt der Messung annimmst, die mit der q-Unsicherheit des Impulses korreliert, dann wäre der Ort, an dem ein einzelnes Quantenobjekt auf ein Target einschlägt, unendlich groß, weil der Impuls beim Einschlag eines Quantenobjektes auf ein Target Null wird.
Mit einer q-Unsicherheit des Ortes v o r der Messung kann ich mich anfreunden, ich habe immer von den Unbestimmtheiten eines einzelnen Quantenobjektes vor der Messung gesprochen, Du interpretierst das immer so, als würde ich von Unsicherheiten reden, die statistischen Ursprungs sind. Ich rede überhaupt nicht von Statistik. Ich rede auch nicht von epistemischen Unsicherheiten. Ich interpretiere die Algebra auch nicht statistisch, ich sage nur, mit dem mathematischen Apparat kannst Du Erwartungswerte vorhersagen – unter der Voraussetzung die Bornsche Regel zählt zu diesem Apparat. Insofern kannst Du Meßwerte mit dem Apparat vorhersagen, in diesem Sinne ist das gemeint. Du mußt mit einer zur Theorie gehörenden Mathematik Vorhersagen machen können, sonst kannst Du sie vergessen.
Wenn die Physik Vorhersagen aus einer Mathematik herauszwingt, dann ist immer ziemlicher Pragmtismus im Spiel. Interessant ist doch nur: was ist vor der Messung, also unabhängig von der Beobachtung gegeben, wie kann ich diese Situation beschreiben. Und unabhängig davon stellt sich die Frage, wie beschreibe ich den Übergang des Objektes samt seiner Umgebung vom Zustand vor der Messung, der eine Unbestimmtheit in sich hat, zu einem Zustand, der keine Unbestimmtheit mehr hat. Über beides gibt die die Algebra etwas preis, die Frage ist, was sagt sie dir?
Mein zentrales Anliegen in diesem Beitrag war, zunächst den Zustand vor der Messung zu beschreiben, den eines einzelnen Quantenobjektes, das nicht wechselwirkt, und zwar mit der Mathematik – aufsetzend auf der Frage, warum erfolgt diese Beschreibung mittels einer Wellenfunktion der Schrödingerschen Wellenmechanik.
Wir können aber auch gerne zunächst nur die Unbestimmtheiten eines quantenmechanischen Objektes vor der Messung ins Auge fassen. Nur sollte das dann auch grundlegend diskutiert werden. Dazu müßtest Du sagen, was genau Du unter q-Unsicherheit als intrinsische Unsicherheit vor der Messung verstehst. Wenn das die Unschärfe ist, die delta x* delta p = n*h (n > 1) zum Ausdruck kommt, dann kann man darauf aufbauen.
Grüße
Bernd |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 14. Mai 2020 20:32 Titel: Bernd Stein Verfasst am: 14. Mai 2020 20:32 Titel: |
 |
|
Hi Tom,
Du kommst scheinbar wieder mit einer Alternative zu meinem Begründungsansatz, nämlich mit einer Aufstellung mathematischer Axiome. Was bezweckst Du damit ? Willst du ein Verständnis der Quantenphysik auf diesen Axiomen aufbauen ? Du weißt doch, dass die Axiome nicht reichen, Du musst zusammen mit den Axiomen dann auch sagen, was die Terme in der axiomatisch vorgestellten Mathematik bedeuten.
Sonst stellen Deine Axiome Symbolik ohne Bedeutung dar.
Was bedeutet ein „Zustand“, was für eine „Realität“ repräsentiert der „Hilbertraum“, warum werden physikalische Größen durch Transformationen in diesem Raum dargestellt, und zwar nur durch ganz bestimmte.
Die klassische Physik verwendet ja eine ganz andere Algebra – wieso ?
Aber Du wirst die Bedeutung der mathematischen Terme „normierter Vektor“, „Hilbertraum“ und „Observable“ nicht finden, wenn Du nur die Mathematik betrachtest. Der sematische Gehalt der Mathematik (eine Interpretation) offenbart sich ja nur aus dem Verhältnis von mathematischer Beschreibung der Welt und einer Beschreibung der Welt mit Begriffen, die eine klare Bedeutung haben. Es nutzt nichts, wenn die Mathematik klar ist, aber die Begriffe nicht.
Um zu klaren Begriffen zu kommen, habe ich den Vorschlag gemacht, zunächst zu klären, wovon die Mathematik überhaupt spricht, im klassischen wie qm Fall. Gegenstände sind auf allen Größenskalen immer in einem „Zustand“. Was verleiht einem Zustand eine Identität? Wie beschreibt die Mathematik jeder Theorie einen solchen identifizierbaren Zustand und seine Änderungen ? Wie gelingt es der Mathematik, durch die Vorhersage eines Messwertes die Realität auf direkte, unmittelbare Weise richtig (überprüfbar) zu beschreiben? Wie beschreibt sie die Realität dann mittelbar, außerhalb einer Meßwertvorhersage ? Wie beschreibt die Mathematik einen gemessenen Zustand und den Zustand, der einer Messung vorausgeht ? Du must mit diesen Fragen anfangen.
Wenn Du deine Begriffe nicht auf die Ergebnisse solcher Überlegungen gründest, sondern ad hoc aussuchst, oder die nimmst, die die Lehramtsphysik in ihrem grenzenlosen Pragmatismus verwendet, kriegst Du keine Konsistenz in Deine Interpretation, das ist doch nun die Erfahrung eines Jahrhunderts. Du kriegst nur unbefriedigende Interpretationen, die das Ganze verschiedenartig beleuchten, aber die wirklichen Umrisse im Dunkeln lassen.
Ich folge dem Gedanken, dass die Mathematik das Vorgenannte auf allen Größenordnung im Prinzip in gleicher Weise beschreibt, und dass man für einen Zustand und vor allem seine Identifizierung und auf allen Skalen die gleichen Begriffe verwenden kann - ich habe immerhin eine klare Leitidee !
Denn die Realität macht keinen Sprung beim Übergang vom Großen ins Kleine, sie ist einheitlich, und die Physik muß folglich auch einheitlich sein. Die einheitliche Realität war schließlich zuerst da, und die Physik und Mathematik folgt ihr und nicht umgekehrt.
Grüße
Bernd |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18064
|
 TomS Verfasst am: 14. Mai 2020 20:55 Titel: TomS Verfasst am: 14. Mai 2020 20:55 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Du kommst scheinbar wieder mit einer Alternative zu meinem Begründungsansatz, nämlich mit einer Aufstellung mathematischer Axiome. Was bezweckst Du damit ? Willst du ein Verständnis der Quantenphysik auf diesen Axiomen aufbauen ?
|
Zunächst mal ja - für dich! Weil du nämlich in deinen Argumentationen bisher gezeigt hast, dass du die o.g. Punkte (1 - 3) nicht sauber trennen kannst. Also schreibe ich mal (1) hin, so dass mal irgendwas klar ist.
| Bernd Stein hat Folgendes geschrieben: | | Du weißt doch, dass die Axiome nicht reichen, Du musst zusammen mit den Axiomen dann auch sagen, was die Terme in der axiomatisch vorgestellten Mathematik bedeuten. |
Ja, deswegen oben explizit die Aussage zu kursiv gesetzten Texten.
Sonst stellen Deine Axiome Symbolik ohne Bedeutung dar.
| Bernd Stein hat Folgendes geschrieben: | | Was bedeutet ein „Zustand“ ... |
Was bedeutet „Geschwindigkeit“?
| Bernd Stein hat Folgendes geschrieben: | | Warum werden physikalische Größen durch Transformationen in diesem Raum dargestellt ... |
Warum werden physikalische Systeme im Rahmen der klassischen Mechanik durch Trajektorien in einem symplektischen Raum dargestellt?
| Bernd Stein hat Folgendes geschrieben: | | Die klassische Physik verwendet ja eine ganz andere Algebra – wieso ? |
Antworten auf Warum-Fragen sind notorisch schwierig. Aber es geht noch gar nicht um das Warum hinter dem Formalismus, sondern um die Grundlagen.
| Bernd Stein hat Folgendes geschrieben: | | Es nutzt nichts, wenn die Mathematik klar ist, aber die Begriffe nicht. |
Stimmt. Aber - mit Verlaub - bei index_razor und mir sind Mathematik und Begriffe klar, bei dir eigentlich keines von beiden. Also klären dir das, oder?
| Bernd Stein hat Folgendes geschrieben: | | Wie gelingt es der Mathematik, durch die Vorhersage eines Messwertes die Realität auf direkte, unmittelbare Weise richtig (überprüfbar) zu beschreiben? Wie beschreibt sie die Realität dann mittelbar, außerhalb einer Meßwertvorhersage ? Wie beschreibt die Mathematik einen gemessenen Zustand und den Zustand, der einer Messung vorausgeht ? Du must mit diesen Fragen anfangen. |
Es war mein Vorschlag, dass du das Messproblem nicht ausklammern und dich nicht nur mit freien, nicht wechselwirkenden Teilchen befasst.
Wirf mir also bitte nicht vor, es wäre meine Idee gewesen, das auszublenden, und komm’ jetzt nicht mit der Belehrung, ich solle über das sprechen, was ich zu Beginn schon vorgeschlagen hatte.
| Bernd Stein hat Folgendes geschrieben: | | Wenn Du deine Begriffe nicht auf die Ergebnisse solcher Überlegungen gründest, sondern ad hoc aussuchst, oder die nimmst, die die Lehramtsphysik in ihrem grenzenlosen Pragmatismus verwendet, kriegst Du keine Konsistenz in Deine Interpretation, das ist doch nun die Erfahrung eines Jahrhunderts. Du kriegst nur unbefriedigende Interpretationen, die das Ganze verschiedenartig beleuchten, aber die wirklichen Umrisse im Dunkeln lassen. |
Kann es sein, dass dir die Situation gerade entgleitet und du dir anmaßt, mich ohne fundiertes Wissen - das ich dir für Mathematik, Physik und Wissenschaftstheorie abspreche - belehren zu wollen?
Ich denke, wir beenden das hier.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Mai 2020 21:18 Titel: index_razor Verfasst am: 14. Mai 2020 21:18 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | Hi Index Razor,
die Bornsche Regel gehört nicht zur Algebra, sie ist aber Bestandteil der „Mathematik“ der Quantentheorie.
|
Nein, "Messung" oder "Meßwert" sind keine mathematischen Begriffe.
| Zitat: |
Ohne diese willkürliche Festlegung kommst Du nicht zu einer Messwertvorhersage – ohne diese Regel ist die ganze Mathematik der Quantentheorie zu nichts nutze.
|
Sagt dir das anomale magnetische Moment des Elektrons irgendwas? Was hat das mit der Bornschen Regel zu tun?
Außerdem, wie gelangt man zu Meßwertvorhersagen innerhalb der statistischen Thermodynamik? Diese wird ausschließlich mit statistischen Konzepten begründet. Es gibt aber nichts in den fundamentalen Annahmen der Theorie, was mit der Bornschen Regel vergleichbar wäre.
| Zitat: |
Wichtiger ist: was meinst Du mit „(es kann sein), dass jede der Einzelmessung nicht genauer als die q-Unsicherheit des Ortes.“
|
Damit meine ich, diese Annahme widerspricht weder dem Formalismus der Quantenmechanik, noch irgendeinem empirischen Befund.
| Zitat: |
Wenn die q-Unsicherheit hinreichend groß ist, messe ich dann einen großen verwaschenen Fleck ?
|
Das läßt sich nur beantworten, wenn eine hinreichend genaue Beschreibung des Meßprozesses vorliegt.
| Zitat: |
Ich denke Du hast eine q-Unsicherheit des Ortes v o r der Messung, aber nicht im Moment der Messung.
|
Doch eine q-Unischerheit habe ich immer. Das ist lediglich eine mathematische Größe, vergiß das nicht.
| Zitat: |
Falls du eine intrinsische q-Unsicherheit des Ortes zum Zeitpunkt der Messung annimmst, die mit der q-Unsicherheit des Impulses korreliert, dann wäre der Ort, an dem ein einzelnes Quantenobjekt auf ein Target einschlägt, unendlich groß, weil der Impuls beim Einschlag eines Quantenobjektes auf ein Target Null wird.
|
Tut mir leid, aber das ist kompletter Unsinn. Du verwechselst hier u.a. Impuls und Impulsunschärfe. Allerdings wird auch der Impuls durch den Einschlag nicht null.
| Zitat: |
Mit einer q-Unsicherheit des Ortes v o r der Messung kann ich mich anfreunden, ich habe immer von den Unbestimmtheiten eines einzelnen Quantenobjektes vor der Messung gesprochen, Du interpretierst das immer so, als würde ich von Unsicherheiten reden, die statistischen Ursprungs sind. Ich rede überhaupt nicht von Statistik. Ich rede auch nicht von epistemischen Unsicherheiten. Ich interpretiere die Algebra auch nicht statistisch, ich sage nur, mit dem mathematischen Apparat kannst Du Erwartungswerte vorhersagen – unter der Voraussetzung die Bornsche Regel zählt zu diesem Apparat.
|
Wenn du von der Bornschen Regel und Erwartungswerten redest, redest du auch von Statistik.
| Zitat: |
Insofern kannst Du Meßwerte mit dem Apparat vorhersagen, in diesem Sinne ist das gemeint. Du mußt mit einer zur Theorie gehörenden Mathematik Vorhersagen machen können, sonst kannst Du sie vergessen.
|
Das kann ich ja: "Das anomale magnetische Moment des Elektrons beträgt }) ." Hat mit der Bornschen Regel nichts zu tun. ." Hat mit der Bornschen Regel nichts zu tun.
| Zitat: |
Und unabhängig davon stellt sich die Frage, wie beschreibe ich den Übergang des Objektes samt seiner Umgebung vom Zustand vor der Messung, der eine Unbestimmtheit in sich hat, zu einem Zustand, der keine Unbestimmtheit mehr hat.
|
Durch eine Schrödingergleichung bzw. eine stochstische Differentialgleichung wenn zufällige Einflüsse der Umgebung berücksichtigt werden müssen. Es ist allerdings keineswegs notwendig, daß dabei die Unschärfe der gemessenen Größe verschwindet.
| Zitat: |
Mein zentrales Anliegen in diesem Beitrag war, zunächst den Zustand vor der Messung zu beschreiben, den eines einzelnen Quantenobjektes, das nicht wechselwirkt, und zwar mit der Mathematik – aufsetzend auf der Frage, warum erfolgt diese Beschreibung mittels einer Wellenfunktion der Schrödingerschen Wellenmechanik.
|
Ich weiß. Meine Kritik daran ist ja auch immer noch im wesentlichen unbeantwortet.
| Zitat: |
Wir können aber auch gerne zunächst nur die Unbestimmtheiten eines quantenmechanischen Objektes vor der Messung ins Auge fassen. Nur sollte das dann auch grundlegend diskutiert werden. Dazu müßtest Du sagen, was genau Du unter q-Unsicherheit als intrinsische Unsicherheit vor der Messung verstehst. |
Das habe ich ja schon. Wenn du es genauer wissen willst mußt du genauer fragen. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 14. Mai 2020 23:41 Titel: Bernd Stein Verfasst am: 14. Mai 2020 23:41 Titel: |
 |
|
Hi index
Da schreibst Du mir:
„Meine Definition des Ortes ist auch keine Gleichung, "die eine raumgreifende Welle" beschreibt, sondern eine Gleichung, die einen Vektor, bzw. eine ganze Trajektorie im Raum beschreibt. So werden Orte und Bahnen von Objekten üblicherweise auch in der klassischen Theorie beschrieben.“
Was soll das ? Willst Du mir die Trivialität mitteilen, dass du eine Trajektorie im Raum mit einer mathematischen Gleichung beschreiben kannst. Da haben wir doch gar keine Differenzen.
Ich würde gerne wissen was Du unter dem Begriff „einen Ort haben“ verstehst. Was ist der semantische Inhalt des sprachlichen Ausdrucks „ das Objekt ist an einem Ort“ ? Kann man davon sprechen, dass ein einzelnes Quantenobjekt „an einem Ort ist“ ? Und inwiefern hat dieser Ort grundsätzlich eine q-Unschärfe ? Der Erwartungswert des Ortsoperators ist ein Messergebnis, betroffen sind Orte zum Zeitpunkt einer Messung, ich spreche aber von Orten v o r der Messung.
Vor der Messung ist das Objekt nur potentiell an einem Ort ? Oder hat es dann keinen Ort (im Sinne von Ort einnehmen, nicht im Besitz haben) ? Oder einen q-unscharfen. Was sagt die Mathematik ? Ist das alles nur epistemische Ungewißheit ? Kannst Du überhaupt auf Grundlage der Mathematik eine klare Aussage über den Ort vor der Messung machen ? Das ist doch hier die Frage.
Ich beleuchte die Situation „das Objekt hat einen Ort“ mal von einer anderen Seite: Die Bestimmung „an einem Ort“ ist nur die operationale Zusammenfassung der Tatsache, dass ein Objekt an einem bestimmten Ort auf ein anderes Objekt einwirkt und diese Einwirkung an diesem Ort beobachtbar ist, und daraus direkt geschlossen werden kann, dass das erste Objekt auch an diesem Ort ist.
Ich gebe zu, da ist kompliziert ausgedrückt, aber Eigenschaften sind alles nur Vereinfachungen, eigentlich gibt es gar keine Eigenschaften, sondern jede Eigenschaft lässt sich auf spezifische Wirkungen reduzieren. Intrinsische Eigenschaften sind dann unmöglich, sie sind auch aus logischen Gründen unmöglich. Wenn es um Quantenphysik geht, sollte man die pragmatische Sprechweise vielleicht auch ablegen, also gar nicht von Eigenschaften sprechen. Wir können das vereinbaren, das ganz zu lassen, Du mußt nur zustimmen.
Wo kommen denn die Probleme der Interpretation der Quantenmechanik her ? Der einzelne auf deiner Trajektorie liegende Ort als möglicher Meßwert muß bei der mathematischen Beschreibung aus dem Kontinuum eines Eigenwertspektrums mit einer von den Physikern erfundenen Delta Funktion auf äußerst pragmatische, geradezu unmathematische Weise herausgezaubert werden, um direkt nach dem Zeitpunkt einer Messung wieder zu in eine Gaußkurve zu zerfliessen. Wie willst Du denn diese Mathematik konsistent interpretieren ? Es ist doch wirklich notwendig zu überlegen, was es bedeutet zu sagen, ein Quantenobjekt „ist an einem Ort.“
Man könnte das mal ohne den Begriff „Eigenschaft“ zu versuchen:
Zu sagen „das Objekt hat in allen Zeitpunkten die Möglichkeit einer lokalen Wirkung“, wäre ja schon mal ein Vorschlag.
Schwingt auch eine Unbestimmtheit mit, die wir ja brauchen. Könnte die Mathematik so was als beschreiben, indem sie mathematisch ausdrückt, dass diese Möglichkeit längs einer Trajektorie besteht ?
Ich frage bloss. Ich frage mich mittlerweile allerdings auch, ob Du überhaupt mein Anliegen und meinen Ansatz verstehst, weil Du immer Formalien kritisierst, die für meine eigentlichen Aussagen keine Bedeutung haben. Mir ist wirklich an Deiner inhaltlichen Kritik gelegen. Ich habe zum Beispiel gesagt, dass ein Objekt vor der Messung mehrere Möglichkeiten haben kann, zum Beispiel an einem Ort zu sein. Dann sagst Du aus, „lediglich für die Meßergebnisse gibt es mehrere Möglichkeiten.“ – was sich wie ein Widerspruch anhört. Das ist aber kein Widerspruch. Wenn das Objekt vor der Messung zwei Möglichkeiten für einen Ort hat (zum Beispiel die Unbestimmtheit zweier Spin-Ausrichtungen), dann wird bei einer Messung entweder die oder die andere festgestellt. Klar gibt es für das Meßergebnis zwei Möglichkeiten. Aber die gibt es nur, weil es diese Möglichkeiten vor Messung schon gab ! Die Möglichkeit, dass etwas wird, geht dem Werden nun mal voraus.
Es gibt natürlich auch Leute, die sagen, das Objekt hat zwei Spinausrichtungen vor der Messung. Das ist aber wirklich eine viel dämlichere Ausdrucksweise (sorry, ich finde das so), als zu sagen, es hat zwei Möglichkeiten.
Was würdest Du sagen: hat es zwei Möglichkeiten für eine Spinausrichtung oder hat es zwi Spinausrichtungen.
Du führst auch vieles aus, womit ich sehr einverstanden bin. So führst Du am Ende den Indeterminismus der Entstehung eines Meßergebnisses auf unkontrollierbare Einflüsse bei der WW zurück. Das habe ich auch schon in diesem Beitrag behauptet.
Ich bin in jedem Fall froh, dass Du bereit bist, Dich mit mir zu unterhalten. Es ist zu Deinem und meinem Vorteil. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 14. Mai 2020 23:47 Titel: Bernd Stein Verfasst am: 14. Mai 2020 23:47 Titel: |
 |
|
Sorry, ich sehe jetzt erst, Dass Du mir schon geantwortet hattest.
Auf die q-Unbestimmtheit komme ich noch einmal zurück.
Ich brauche ein bisschen Zeit zum Überlegen.
Danke für Deine Antwort.
Grüße Bernd. |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 15. Mai 2020 01:38 Titel: Bernd Stein Verfasst am: 15. Mai 2020 01:38 Titel: |
 |
|
Hi Tom,
es tut mir leid, dass Du einem Fragen nichts Positives abgewinnen kannst.
Es leider eine Tatsache, dass das, was der mathematische Apparat der Quantenphysik aussagt, in seiner Bedeutung immer noch zu großen Teilen unverstanden ist. Ich meine damit, dass es nicht nur verschiedene Interpretationen gibt (die eigentlich verschiedene Theorien darstellen), sondern dass die begrifflichen Grundlagen nicht klar sind. Es gibt zum Beispiel keinen Konsens darüber, was der physikalische Begriff „Zustand“ im quantenphysikalischen Kontext bedeutet und keiner weiß, was in der Realität mit dem sog. „Überlagerungszustand“ korrespondiert. Ich glaube dass sich mit diesen sogenannten philosophischen Problemen die Grenzen der physikalischen Methode generell abzeichnen, aber das nur am Rande.
Um eine Lösung der philosophischen Probleme wird doch nun seit hundert Jahren gerungen – mit welchem Erfolg? Ein Beitrag von der Wissenschaftsphilosphie kannst Du nicht erwarten, diese hat sich die Theorien, die ihr die Physik zuflüstert, zu eigen gemacht, und sich in die selbstverschuldete Irrelevanz begeben. Wartest Du nun nach hundert Jahren interner Diskussion noch auf einen Geistesblitz aus dem inneren Kreis von Eingeweihten, die die letzten Verästelungen der Algebra analysiert haben, und nun die Nichtlokalität allen Seins konsistent erklären können ? Ich weiss aus zahlreichen Gesprächen, dass die Physiker, die sich des Problems bewusst sind, in Wirklichkeit auf Denkanstösse, auf neue Ideen, von außen warten.
Das alles ist noch kein Dilemma. Zum Dilemma wird es erst, wenn Du dir klar wirst, wie tiefgreifend die Probleme sind, die mit diesen Ideen angepackt werden müssen. Schließlich sind hundert Jahre vergebliche Suche nach der richtigen Interpretation eine lange Zeit und wirklich hervorragende Leute sind daran gescheitert. Da kann man mal nicht mit irgendeiner schlauen Idee kommen, die haben andere schon gehabt. Sie muss an den methodischen Grundlagen angreifen, an den begrifflichen Fundamenten, an den Denkweisen, an Gewohnheiten zum Beispiel, wie ein mathematischer Formalismus betrachtet wird. Es war nun mal zu allen Zeiten so: wer das anfängt, der kriegt Prügel von der etablierten Wissenschaft, die lässt sich bei sowas erst mal gar nichts sagen.
Die Physik ist in ihrem Pragmatismus nicht zimperlich, wenn es sein muss, biegt sie sich die Realität so zurecht, wie sie sie haben will. Sie kommt so immer wieder klar, es ist auch tatsächlich bewundernswert, dass der lamb shift auf 13 Stellen hinter dem Komma richtig vorhergesagt wird. Aber aus philosophischer Sicht kann man sagen, dieser Erfolg ist herbeigefuscht. Damit ist gemeint: wie er zustande kommt, kann nicht konsistent, mit der Logik als Grundlage, erklärt werden. Damit hat die Physik ein Dilemma: im Grunde weiß sie genau, aus ihren Theorien kann sie eine Ontologie dieser Welt nicht ableiten, nur deren Wirkungen kennt sie genau. Aber so kriegt sie immer nur die Hälfte der Welt zu fassen, nicht die Ganze.
Das ist eigentlich das Fatale, dass all diese Probleme bekannt sind, aber wer diese anspricht, der erfährt die Reaktion, wie sie hier stattfindet. Das ist nicht für mich bedauerlich, weil ich von Euch immer profitiere, ich lerne von Euch, ich sehe, wie Ihr argumentiert, mit welcher Denkweise ihr etwas angeht, ich weiss, wo ihr mitkommt, und wo nicht. Ich kann dann meine Argumentation formal verbessern. Du bleibst dagegen frustiert in Deiner Welt zurück, an der Du nicht rütteln lässt. Natürlich würdest Du das, aber nur von Leuten, die was von Mathematik verstehen.
Diese Haltung ist einer der Gründe (nicht allein), warum alle Arbeitsgruppen Physik + Philosophie nach wenigen Jahren an deutschen Universitäten eingegangen sind, und die Thematik nun brach liegt.
Grüße Bernd |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18064
|
 TomS Verfasst am: 15. Mai 2020 06:50 Titel: TomS Verfasst am: 15. Mai 2020 06:50 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | es tut mir leid, dass Du einem Fragen nichts Positives abgewinnen kannst.
|
Deinen Fragen schon, nicht jedoch unhaltbaren oder schlicht falschen Behauptungen.
| Bernd Stein hat Folgendes geschrieben: | | Ein Beitrag von der Wissenschaftsphilosphie kannst Du nicht erwarten, diese hat sich die Theorien, die ihr die Physik zuflüstert, zu eigen gemacht, und sich in die selbstverschuldete Irrelevanz begeben. |
Du hast offenbar kein einziges Paper oder Fachbuch zu diesen Themen gelesen, sonst würdest das so nicht behaupten.
| Bernd Stein hat Folgendes geschrieben: | | Zum Dilemma wird es erst, wenn Du dir klar wirst, wie tiefgreifend die Probleme sind. |
Da ich mich seit längerem eingehend damit befasse, sind mir die Probleme und diverse Lösungsansätze sehr wohl bewusst.
| Bernd Stein hat Folgendes geschrieben: | Es war nun mal zu allen Zeiten so: wer das anfängt, der kriegt Prügel von der etablierten Wissenschaft, die lässt sich bei sowas erst mal gar nichts sagen
...
Das ist eigentlich das Fatale, dass all diese Probleme bekannt sind, aber wer diese anspricht, der erfährt die Reaktion, wie sie hier stattfindet. |
Du bekommst deswegen „Prügel“, weil du dich offenbar dazu berufen fühlst, der etablierten Wissenschaft hier etwas beibringen zu wollen, obwohl deine Beiträge zeigen, dass du noch nicht mal den Gegenstand deiner Kritik verstanden hast.
Du erinnerst mich an jemanden, der eine Neuinterpretation der griechischen Tragödie anstrebt, ohne Altgriechisch gelernt zu haben.
Das zeigt übrigens auch dein Dialog mit index_razor: seine Beiträge sind sehr präzise und klar; du weigerst dich jedoch beharrlich, dich gründlich damit auseinanderzusetzen.
Das in Summe lässt dein Ansinnen ziemlich anmaßend erscheinen.
Zu meinem Vorschlag, das axiomatisch und noch frei von einer speziellen Interpretation anzugehen: der steht weiterhin, aber dazu müsstest du dich darauf einlassen. Ein Fehler wäre das nicht, denn der mathematische Kern bleibt ohnehin unangetastet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Mai 2020 10:58 Titel: index_razor Verfasst am: 15. Mai 2020 10:58 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: |
Da schreibst Du mir:
„Meine Definition des Ortes ist auch keine Gleichung, "die eine raumgreifende Welle" beschreibt, sondern eine Gleichung, die einen Vektor, bzw. eine ganze Trajektorie im Raum beschreibt. So werden Orte und Bahnen von Objekten üblicherweise auch in der klassischen Theorie beschrieben.“
Was soll das ? Willst Du mir die Trivialität mitteilen, dass du eine Trajektorie im Raum mit einer mathematischen Gleichung beschreiben kannst.
|
Du hast irgendeine irrelevante Bemerkung über Gleichungen für "raumgreifende Wellen" gemacht. Ich wollte dir nur klar machen, daß diese Bemerkung irrelevant war.
Ansonsten wollte ich dir mitteilen, daß es solche Trajektorien auch in der QM gibt. Die Frage ist nur wie man sie interpretiert. Man kann sie als Trajektorien einzelner Systeme im Raum ansehen oder als zeitabhängige Mittelwerte eines Ensembles. Aber man kann nicht behaupten, es gäbe sie im Formalismus nicht, wie du es oft getan hast.
| Zitat: |
Ich würde gerne wissen was Du unter dem Begriff „einen Ort haben“ verstehst. Was ist der semantische Inhalt des sprachlichen Ausdrucks „ das Objekt ist an einem Ort“ ?
|
Du kannst gern diese umgangssprachliche Phrase semantisch durchanalysieren, aber ohne mich. Du hältst das vermutlich für die philosophische Herangehensweise. Aber ich denke außer Wortklauberei wird dabei nichts rauskommen.
Mir reicht die Feststellung, daß man dem Satz "Das Objekt befindet sich am Ort X" in der QM eine völlig analoge Bedeutung geben kann, wie in der klassischen Physik. Damit ist nämlich klar, daß hier überhaupt kein speziell quantenmechanisches Problem vorliegt. Und außerdem ist mir die klassische Bedeutung verständlich genug.
| Zitat: |
Vor der Messung ist das Objekt nur potentiell an einem Ort ? Oder hat es dann keinen Ort (im Sinne von Ort einnehmen, nicht im Besitz haben) ? Oder einen q-unscharfen. Was sagt die Mathematik ? Ist das alles nur epistemische Ungewißheit ? Kannst Du überhaupt auf Grundlage der Mathematik eine klare Aussage über den Ort vor der Messung machen ? Das ist doch hier die Frage.
|
Ich verstehe nicht, was dich ständig dazu treibt, mir immer wieder dieselben Fragen zu stellen, als hätte ich noch nie eine Antwort darauf gegeben. Anstatt mir jedes mal wieder zu erklären, was hier doch die Frage ist, die ich längst verstanden und beantwortet habe, könntest du doch zur Abwechslung mal meine Antworten zur Kenntnis nehmen und gegebenenfalls Einwände formulieren.
| Zitat: |
Ich beleuchte die Situation „das Objekt hat einen Ort“ mal von einer anderen Seite: Die Bestimmung „an einem Ort“ ist nur die operationale Zusammenfassung der Tatsache, dass ein Objekt an einem bestimmten Ort auf ein anderes Objekt einwirkt und diese Einwirkung an diesem Ort beobachtbar ist, und daraus direkt geschlossen werden kann, dass das erste Objekt auch an diesem Ort ist.
|
Das ist schön für dich. Solange du nicht behauptest, es gäbe im QM-Formalismus nichts, was als "Ort des Objekts vor und nach und während der Messung" interpretierbar ist, habe ich absolut nichts gegen deine semantischen Spielereien, auch wenn ich kein Interesse habe, mich daran zu beteiligen.
| Zitat: |
Ich gebe zu, da ist kompliziert ausgedrückt, aber Eigenschaften sind alles nur Vereinfachungen, eigentlich gibt es gar keine Eigenschaften, sondern jede Eigenschaft lässt sich auf spezifische Wirkungen reduzieren. Intrinsische Eigenschaften sind dann unmöglich, sie sind auch aus logischen Gründen unmöglich. Wenn es um Quantenphysik geht, sollte man die pragmatische Sprechweise vielleicht auch ablegen, also gar nicht von Eigenschaften sprechen. Wir können das vereinbaren, das ganz zu lassen, Du mußt nur zustimmen.
|
Nein, da stimme ich ganz sicher nicht zu. Ich halte es für sinnvoll und nützlich von objektiven Eigenschaften zu reden und will das auch in der QM tun.
| Zitat: |
Wo kommen denn die Probleme der Interpretation der Quantenmechanik her ? |
Ich denke daher, daß man undefinierte Begriffe wie "Messung" und "Meßwert" in den Grundpostulaten verwendet, so als hätten sie einen eindeutigen, mathematisch präzisen Sinn.
| Zitat: |
Der einzelne auf deiner Trajektorie liegende Ort als möglicher Meßwert muß bei der mathematischen Beschreibung aus dem Kontinuum eines Eigenwertspektrums mit einer von den Physikern erfundenen Delta Funktion auf äußerst pragmatische, geradezu unmathematische Weise herausgezaubert werden, um direkt nach dem Zeitpunkt einer Messung wieder zu in eine Gaußkurve zu zerfliessen.
|
Ich glaube dir ist immer noch nicht klar, daß eine einzelne Ortsmessung durchaus etwas anderes ergeben kann als den objektiven Ort. Außerdem ist es weder nötig noch sonst wie problematisch, daß sich der Zustand während der Messung in eine delta-Funktion verwandelt. Wieder mal trägst du hier äußerst fragwürdige Behauptungen vor, als gäbe es nichts selbstverständlicheres.
| Zitat: |
Ich frage bloss. Ich frage mich mittlerweile allerdings auch, ob Du überhaupt mein Anliegen und meinen Ansatz verstehst, weil Du immer Formalien kritisierst, die für meine eigentlichen Aussagen keine Bedeutung haben. Mir ist wirklich an Deiner inhaltlichen Kritik gelegen.
|
Möglicherweise verstehst du nicht genug vom Thema um relevante inhaltliche Kritik von irrelevanten Formalitäten zu unterscheiden? Nur so als Denkanstoß...
| Zitat: |
Ich habe zum Beispiel gesagt, dass ein Objekt vor der Messung mehrere Möglichkeiten haben kann, zum Beispiel an einem Ort zu sein. Dann sagst Du aus, „lediglich für die Meßergebnisse gibt es mehrere Möglichkeiten.“ – was sich wie ein Widerspruch anhört. Das ist aber kein Widerspruch.
|
Widersprochen habe ich deiner Aussage, daß "das Objekt vor der Messung zwei Möglichkeiten für einen Ort hat". Ich behaupte ja es hat nur einen Ort. Dann muß ich natürlich erklären können, wieso trotzdem bei einer Ortsmessung mal das eine und mal das andere Ergebnis herauskommen kann. Das tue ich indem ich sage, der physikalische Prozeß, den du hier als "Ortsmessung" bezeichnest, erzeugt lediglich ein sehr verrauschtes Signal für den tatsächlichen Ort, wobei, qualitativ gesprochen, das Rauschen mindestens so groß ist wie die Ortsunschärfe.
| Zitat: |
Was würdest Du sagen: hat es zwei Möglichkeiten für eine Spinausrichtung oder hat es zwi Spinausrichtungen.
|
Weder noch. Ich würde sagen es hat einen Spin (oder von mir aus eine "Spinausrichtung"). |
|
 |
Bernd Stein
Anmeldungsdatum: 28.10.2019
Beiträge: 41
|
 Bernd Stein Verfasst am: 15. Mai 2020 22:17 Titel: Bernd Stein Verfasst am: 15. Mai 2020 22:17 Titel: |
 |
|
Hi index razor
Ich hab noch mal die Statements zusammengefasst:
Meine Annahme sin in Schrägsschrift angegeben. Es kommt nicht auf alle Details an, sondern nur darauf, wie ich das Ganze unten interpretiere.
Man kann nicht sagen, dass ein physikalisches Objekt vor der Messung Eigenschaften besitzt. Die Frage stellt sich daher, wie soll ich das Quantenobjekt beschreiben, wenn es keine solche Eigenschaften „hat“ ? Wenn ich aus den mathematischen Gleichungen dazu nichts Verbindliches herauslesen kann, welche Grundlage habe ich dann für eine passende Beschreibung ?
„eine dynamische Größe G besitzt im Zustand eine Reihe von Eigenschaften völlig unabhängig von jeglicher Messung, z.B. den Erwartungswert , die Unschärfe usw.“ (Tom: „Dabei handelt es sich nicht um die von dir erwarteten klassischen Eigenschaften oder Messgrößen, aber das ist das Problem deiner Erwartungshaltung und dem zumeist nicht ausreichend definierten Begriff der Messung.“)
danke für Deinen Kommentar, den ich allerdings nicht so ganz verstehe. Was soll der „Erwartungswert“ oder die „Unschärfe“ für eine Eigenschaft sein ?
Wenn man sich nicht von vornherein auf eine statistische Interpretation festlegen will, kann man einfach die quantenmechanischen "Erwartungswerte" mit den zugehörigen physikalische Größen identifizieren. Diese folgen bis auf "Quantenkorrekturen", die durch die Unschärfen abgeschätzt werden können, den klassischen Gleichungen. Die Frage, was der "Impulserwartungswert" für eine Eigenschaft sein soll, bekommt also genau dieselbe Antwort wie die Frage was der Impuls für eine Eigenschaft sein soll. Die Unschärfen selbst sind rein quantenmechanische Größen ohne klassische Entsprechung. …. Wenn man dies nicht voraussetzt, ist es kein Problem davon zu sprechen, daß ein Quantensystem alle diese Eigenschaften (und noch mehr) hat. Hinzu kommen noch Eigenschaften, die es in der klassischen Physik nicht gibt, wie z.B. alle Unschärfen dieser Größen. Über alle diese Größen macht die Theorie aber deterministische, eindeutige Aussagen. Es handelt sich also um sehr wohldefinierte Eigenschaften von Quantenobjekten. …. Das ist ein Fakt, der völlig ohne Umschweife aus dem Formalismus folgt. … Der Streitpunkt ist höchstens, was diese Werte dann am Ende mit Messergebnissen zu tun haben. … Du hast dieselben Eigenschaften der klassischen Theorie wie Ort, Impuls, Drehimpuls, Energie etc. auch in der nichtrelativistischen QM. Der Unterschied ist nur, daß diese Eigenschaften dort anderen Gesetzen folgen. Das ist natürlich wenig überraschend.
(Einwand Tom: index_razor hat bereits darauf hingewiesen, dass du in einem abgeschlossen Quantensystem immer noch einen Satz an Observablen benötigst, die dir zusammen mit der Schrödingergleichung “Eigenschaften” des Quantensystems liefern.) mein Kommentar: Anführungszeichen beachten !
Dazu hatte ich ausgeführt, dass man aus dem mathematischen Formalismus gerade das nicht herauslesen kann, dass nämlich ein Quantenobjekt im Allgemeinen, also wenn es sich nicht in einem besonderen Zustand befindet, und erst recht im Sonderfall oder in der Idealisierung als „freies Teilchen, vor einer Messung keine definierten physikalischen Eigenschaften wie Ort, Impuls oder Energie hat, und zwar deshalb, weil die Mathematik in diesem Fall über diese Bestimmungsgrößen nichts aussagt.
Nochmal, das ist falsch. Die Mathematik der QM macht gerade über alle diese Größen in jedem Zustand, zu jedem Zeitpunkt (insbesondere vor einer Messung) konkrete Aussagen. Die Frage ist nur, wie man diese Werte interpretiert. Da hat sich nun die Ansicht durchgesetzt, daß sie nicht die realen Eigenschaften eines individuellen Systems repräsentieren. Das liegt aber nicht daran, daß es sie gar nicht gibt, sondern nur daran, daß davon ausgegangen wird, nur Eigenwerte von Observablen könnten solche Eigenschaften repräsentieren …. Dann erkläre mir doch mal genau und ohne Umschweife, was dich daran hindert, einem "Quantenobjekt" zu jeder Zeit und unabhängig von irgendeiner Messung eindeutig einen bestimmten Ort, einen bestimmten Impuls, eine bestimmte Energie, etc. zuzuordnen. Das habe ich jetzt immer noch nicht verstanden.
Ich wollte von dir wissen, warum du den einen konkreten Ort und den einen konkreten Impuls die ich direkt aus der Lösung der Schrödingergleichung und Observablenalgebra abgeleitet habe, nicht als objektive Eigenschaften des Quantensystems ansehen willst.
ein eindeutiger Wert wird einem Quantenobjekt durch Messung zugewiesen
Ein Meßvorgang wird aber von der SG und der Algebra nicht beschrieben.
Was sagt der mathematische Apparat über den Ort v o r der Messung aus ?
Das beantworte ich jetzt mindestens zum dritten mal (mein Einschub: Erwartungswert der Ortsobservalblenoperators). Zumindest halte ich das für eine mögliche Interpretation des Ortes eines einzelnen Quantenobjekts. Es wäre hilfreich, wenn du diese Antwort jetzt mal zur Kenntnis nimmst und gegebenenfalls klar machst, was du dagegen für Einwände hast. Dieser Ort besitzt allerdings eine intrinsische Unsicherheit, gegeben durch die quantenmechanische Ortsunschärfe ("q-uncertainty"). Das bedeutet aber nicht, daß es sich bei dem Ortserwartungswert nicht um eine objektive Eigenschaft eines Individuums handeln kann.
Zumindest halte ich das für eine mögliche Interpretation des Ortes eines einzelnen Quantenobjekts.
Dieser Ort besitzt allerdings eine intrinsische Unsicherheit, gegeben durch die quantenmechanische Ortsunschärfe ("q-uncertainty").
Deine Frage war was der mathematische Formalismus über den Ort aussagt. Antwort: Unter anderem: der Ortserwartungswert. Daß es sich bei diesem um den "Ortserwartungswert einer Vielzahl von Messungen" handelt, ist nur deine Interpretation auf Basis der Bornschen Regel, die nicht zum formalen, mathematischen Kern der Quantenmechanik gehört. Nur darum geht es. Du kannst von mir aus gern die ganze statistische Interpretation einfach weiterhin unhinterfragt übernehmen. Was du nicht kannst, ist, Behauptungen über den mathematischen Formalismus daraus ableiten.
Was können wir als eine im Konsens verstandene Wahrheit aus der Symbolik der Mathematik als wahr herauslesen,
Wir können herauslesen, daß der Ortserwartungswert der (unsichere) Ort eines individuellen Systems ist.
Wir können bekanntlich auch etwas anderes herauslesen. Es ist ja nichts neues, daß im Falle der QM verschiedene Interpretationen desselben Formalismus im Umlauf sind. (mein Einschub: das war keine Antwort).
Mir reicht die Feststellung, daß man dem Satz "Das Objekt befindet sich am Ort X" in der QM eine völlig analoge Bedeutung geben kann, wie in der klassischen Physik. Damit ist nämlich klar, daß hier überhaupt kein speziell quantenmechanisches Problem vorliegt. Und außerdem ist mir die klassische Bedeutung verständlich genug.
(Einwand von Tom: Neben vielen anderen Begriffsverwirrungen in diesem Thread stört auch die fehlende Definition, auf was sich der Zustandsvektor bezieht und was mit "Eigenschaft" gemeint ist. Evtl. wird hier implizit "klassische Eigenschaft" verstanden; das ist natürlich ein ungerechtfertigtes Vorurteil. Wenn der Zustandsvektor ein einzelnes System im ontischen Sinne beschreibt, dann ist genau dieser Zustandsvektor die wesentliche Eigenschaft des Systems - bezogen auf die durch die Observablenalgebra feiner definierte Geometrie des Hilbertraumes.) … In völlig analoger Weise liefert der quantenmechanische Zustandsvektor eine ausrechende Beschreibung, wenn ich ihn im Kontext der physikalisch relevanten Observablenalgebra verstehe, d.h. seine Projektionen auf die Eigenzustände der Observablen kenne, also (theta, phi, ...)
Kannst Du überhaupt auf Grundlage der Mathematik eine klare Aussage über den Ort vor der Messung machen ?
Ich verstehe nicht, was dich ständig dazu treibt, mir immer wieder dieselben Fragen zu stellen, als hätte ich noch nie eine Antwort darauf gegeben. Anstatt mir jedes mal wieder zu erklären, was hier doch die Frage ist, die ich längst verstanden und beantwortet habe, könntest du doch zur Abwechslung mal meine Antworten zur Kenntnis nehmen und gegebenenfalls Einwände formulieren. … Ich behaupte ja es hat nur einen Ort. Dann muß ich natürlich erklären können, wieso trotzdem bei einer Ortsmessung mal das eine und mal das andere Ergebnis herauskommen kann. Das tue ich indem ich sage, der physikalische Prozeß, den du hier als "Ortsmessung" bezeichnest, erzeugt lediglich ein sehr verrauschtes Signal für den tatsächlichen Ort, wobei, qualitativ gesprochen, das Rauschen mindestens so groß ist wie die Ortsunschärfe. (Mein Kommentar: also den einen Ort hat es doch nur durch Messung ?)
"Messung" oder "Meßwert" sind keine mathematischen Begriffe.
(Komentar Tom: Ein Ausblenden des Messproblems führt m.E. in eine Sackgasse, aber lassen wir das beiseite.)
Hi indes razor,
ich habe das zusammengestellt, erstens um mich bei Dir zu bedanken, daß du mit jemandem wie mir, der dich penetrant ärgert, so viel Geduld aufbringst, und sachbezogen antwortest. Ich weiss das zu schätzen. Zweitens habe ich das zusammengestellt, um Dir zu zeigen, dass es keinesfalls einfach ist, Dich zu verstehen. Statt mir zu sagen, wie ich gehofft habe, wo meine Beschreibung der Propagation eines freien Quantenobjektes mittels sukkzessiver Identitätsabbildungen dem sicheren Wissen widerspricht, sagst Du, diese Ausführungen seien ein Sammelsurium von Wirrheiten und behauptest dann, ein Quantenobjekt würde mit "klassischen" Eigensachaften entsprechenden Eigenschaften (bis auf Unschärfen) propagieren – obwohl ich nicht einmal da weiß, ob ich Dich in diesem Punkt richtig verstanden habe.
Deine Behauptungen, das dies sei unumstößlich so oder so, ist in Wirklichkeit eine Interpretation der Theorie, und kein gesichertes Wissen, was sich Dir von Anfang an nicht abgenommen habe - deswegen meine Penetranz. Es gibt aber nun mal keine wahre Interpretation, sondern nur strittige, und das ist auch gut so. Was mich stört ist, dass Du mir gegenüber so tust, als sei Deine Interpretation die Wahrheit schlechthin.
Es mag gute Gründe für Deinen Standpunkt geben. Die Erwartungswerte der Observablen kann man auch anders interpretieren als Du. Am Ende hast Du das ja auch angedeutet. Ich bin ebenso wie Tom der Meinung, am Ende würdest Du Dich dem auch anschließen, das der Eigenschaftsbegriff nicht das Gelbe vom Ei ist. Welche Eigenschaft soll ein Zustand haben, der sich mathematisch als Überlagerung anderer Zustände darstellen läßt? Natürlich ist das keine Eigenschaft, die zu einem Eigenzustand, gehört, aber was für eine ist definierte (?) es dann? Du hat nach meiner Ansicht in jeder Interpretation ein Begriffsproblem. Die Begriffe lassen sich, anders als Tom das behauptet, von der mathematischen Symbolik nicht trennen, eine Binsenwahrheit, die zu behaupten mir vorgeworfen wird – aber solche Vorwürfe sind alles Lappalien. Worauf es mir ankommt ist: die Diskussion in einer Weise zu führen, wie Du das hier gemacht hast, halte ich nicht für in Ordnung.
Ich habe eigentlich nur überlegt habe, ob man die Propagation eines einzelnen Quantenobjekts (ohne Eigenschaften) nicht anders beschreiben kann, als über das mathematische Artefakt einer Wellenfunktion, die jeder Anschaulichkeit entbehrt. Das hast Du relativ schnell als Unsinn deklariert, und Deine Version einer Interpretation von Eigenschaften eines Quantenobjektes/systems zu präsentieren, so als ob dies der Weisheit letzter Schluss sei, obwohl es nur eine Interpretation ist. Nochmal: es gibt in der Wissenschaft keine Wahrheit, nur Sichtweisen, für die man werben kann.
Trotzdem bin ich Dir dankbar. Ich habe herausgehört, dass die Observablenalgebra durchaus Ähnlichkeit mit dem Phasenraum hat, ja man kann ihn als quantenmechanisches Äquivalent ansehen, mit einem strukturellen Gefüge, in deren Tiefen physikalische Eigenschaften ihrer vielfältigen Dechiffrierung entgegen schlummern. Vor allem sehe ich, das das, was eine Messung ist, die ich in philosphischer Non-Chalance als Beseitung von Unbestimmtheiten bezeichnet habe (im realen Experiment ebenso wie durch mathematische Operation der Berechnung eines Meßwertes) ziemlich unverstanden ist, physikalisch noch weniger als metaphysisch.
Es wäre doch interessant, Du würdest mal einen Thread aufmachen, um das zu diskutieren. Ich würde gerne daran teilnehmen.
Es grüßt Dich
in wissenschaftlicher Verbundenheit
Bernd |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Mai 2020 23:01 Titel: index_razor Verfasst am: 15. Mai 2020 23:01 Titel: |
 |
|
| Bernd Stein hat Folgendes geschrieben: | | Statt mir zu sagen, wie ich gehofft habe, wo meine Beschreibung der Propagation eines freien Quantenobjektes mittels sukkzessiver Identitätsabbildungen dem sicheren Wissen widerspricht, sagst Du, diese Ausführungen seien ein Sammelsurium von Wirrheiten |
Erst nachdem meine Kritik inklusive konkreter Fragen nach der Bedeutung verwendeter Ausdrücke unbeantwortet geblieben sind.
| Zitat: |
und behauptest dann, ein Quantenobjekt würde mit "klassischen" Eigensachaften entsprechenden Eigenschaften (bis auf Unschärfen) propagieren – obwohl ich nicht einmal da weiß, ob ich Dich in diesem Punkt richtig verstanden habe.
Deine Behauptungen, das dies sei unumstößlich so oder so, ist in Wirklichkeit eine Interpretation der Theorie, und kein gesichertes Wissen, was sich Dir von Anfang an nicht abgenommen habe - deswegen meine Penetranz.
|
Hier nochmal was ich oben als "Fakt" bezeichnet habe:
| index_razor hat Folgendes geschrieben: | | Bernd Stein hat Folgendes geschrieben: |
Dass man aus dem mathematischen Formalismus der Quantenmechanik alles mögliche herausdeuten kann, ist mir bekannt, und meinetwegen mag man da herausdeuten, dass man Quantenobjekten vor der Messung einen "Erwartungswert" für einen Energiewert oder einen Impuls, also Werte für diese Eigenschaften in einer ontologischen Schwankungsbreite, zuordnen kann.
|
Da gibt es nicht viel zu deuten. Das ist ein Fakt, der völlig ohne Umschweife aus dem Formalismus folgt. (Bis auf das "ontologisch" natürlich, was aber nicht von mir stammt.)
|
Ich habe hier also nicht von irgendeiner Interpretation gesprochen, sondern von der formalen QM-Definition von Erwartungswerten ) , d.h. q-Erwartungswerten und q-Unschärfen, etc. , d.h. q-Erwartungswerten und q-Unschärfen, etc.
| Zitat: |
Es gibt aber nun mal keine wahre Interpretation, sondern nur strittige, und das ist auch gut so. Was mich stört ist, dass Du mir gegenüber so tust, als sei Deine Interpretation die Wahrheit schlechthin.
|
Daß ich so täte, bildest du dir allerdings nur ein.
| Zitat: |
Es mag gute Gründe für Deinen Standpunkt geben. Die Erwartungswerte der Observablen kann man auch anders interpretieren als Du. Am Ende hast Du das ja auch angedeutet. Ich bin ebenso wie Tom der Meinung, am Ende würdest Du Dich dem auch anschließen, das der Eigenschaftsbegriff nicht das Gelbe vom Ei ist. Welche Eigenschaft soll ein Zustand haben, der sich mathematisch als Überlagerung anderer Zustände darstellen läßt?
|
Zum x-ten mal: Alle q-Erwartungswerte können solche Eigenschaften sein. Diese sind jedem Zustand zugeordnet.
| Zitat: |
Natürlich ist das keine Eigenschaft, die zu einem Eigenzustand, gehört, aber was für eine ist definierte (?) es dann? Du hat nach meiner Ansicht in jeder Interpretation ein Begriffsproblem. Die Begriffe lassen sich, anders als Tom das behauptet, von der mathematischen Symbolik nicht trennen, eine Binsenwahrheit, die zu behaupten mir vorgeworfen wird – aber solche Vorwürfe sind alles Lappalien. Worauf es mir ankommt ist: die Diskussion in einer Weise zu führen, wie Du das hier gemacht hast, halte ich nicht für in Ordnung.
|
Ich bin schwer getroffen.
| Zitat: |
Ich habe eigentlich nur überlegt habe, ob man die Propagation eines einzelnen Quantenobjekts (ohne Eigenschaften) nicht anders beschreiben kann, als über das mathematische Artefakt einer Wellenfunktion, die jeder Anschaulichkeit entbehrt. Das hast Du relativ schnell als Unsinn deklariert, und Deine Version einer Interpretation von Eigenschaften eines Quantenobjektes/systems zu präsentieren, so als ob dies der Weisheit letzter Schluss sei, obwohl es nur eine Interpretation ist.
|
Du hast absolut gar nichts verstanden. Du hast eine Behauptung über den mathematischen Formalismus aufgestellt, nämlich, daß es unmöglich sei, aus ihm objektive Eigenschaften einzelner Quantenobjekte zu berechnen oder etwas dergleichen. Diese Behauptung beruhte aber nicht auf dem Formalismus allein, sondern auf deiner Interpretation der q-Erwartungswerte als statistische Größen.
Ich widerlege nun deine Behauptung, indem ich eine alternative Interpretation desselben Formalismus angebe, in der diese Behauptung nicht gilt und q-Erwartungswerte stattdessen objektive Eigenschaften individueller Systeme sind.
Deswegen behaupte ich aber noch nicht, diese alternative Interpretation sei der Weisheit letzter Schluß. Ich habe die ganze Zeit nur behauptet, diese Alternative sei möglich. Und mehr muß ich auch nicht behaupten.
| Zitat: |
Trotzdem bin ich Dir dankbar. Ich habe herausgehört, dass die Observablenalgebra durchaus Ähnlichkeit mit dem Phasenraum hat,
|
Oje, naja, viel Spaß mit deinem neu erworbenen "Wissen", aber bitte zitiere mich nicht damit. |
|
 |
|
|















