| Autor |
Nachricht |
Nic_7
Anmeldungsdatum: 29.09.2023
Beiträge: 1
|
 Nic_7 Verfasst am: 29. Sep 2023 12:54 Titel: Kraft auf einen Punkt durch Kugelladungen |
 |
|
Meine Frage:
Hallo zusammen, ich habe folgende Aufgabe gestellt bekommen:
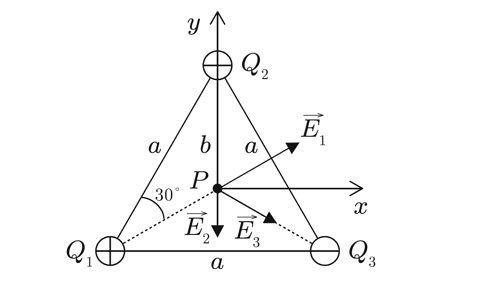
Drei Punktladungen1198761 =2,5·10^?8 As,1198763 =1,5·10^?8 As und 1198762 =?2·10^-8 As sind in den Eckpunkten eines gleichseitigen Dreiecks mit der Seitenlänge 119886 = 10 cm, in der Luft angebracht. Legen Sie den Ursprung eines kartesischen 2D?Koordinatensystems in den Mittelpunkt P des
Dreiecks und berechnen Sie:
a)Die Beträge der drei elektrischen Feldstärken, die von den drei Ladungen in dem Mittelpunkt P erzeugt werden.
b)Den Betrag der resultierenden Feldstärke in dem Mittelpunkt.
c)Den Winkel ? der resultierenden Feldstärke mit der horizontalen x?Achse.
Willkommen im Physikerboard!
Ich habe das Bild aus dem externen Link als Anhang eingefügt. Bitte verwende keine solchen Links, die sind irgendwann ungültig.
Viele Grüße
Steffen
Ich habe versucht das ganze zu berechnen, nur stimmen meine Ergebnisse nicht mit der der Lösung überein. Könnte mir eventuell jemand erklären, was ich genau tun muss bzw. den Rechenweg aufzeigen?
Meine Ideen:
Lösungen: a)1198641 = 6,75 ? 10^4 Vm?1 1198642 = 4,05 ? 10^4 Vm?1 1198643 = 5,4 ? 104 Vm?1
b) |119864|=11,05?104 Vm
c) 120572 ? 18°
| Beschreibung: |
|
| Dateigröße: |
28.39 KB |
| Angeschaut: |
5314 mal |
|
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 29. Sep 2023 15:37 Titel: |
|
|
Wo liegt der Schwerpunkt P des gleichseitigen Dreiecks und welchen Abstand r_1, r_2 und r_3 haben die Ecken 1,2,3 vom Schwerpunkt P.
Der Betrag der Feldstärken |E_1|, |E_2| und |E_3| ist umgekehrt proportional zu r^2.
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
| Myon Verfasst am: 29. Sep 2023 16:27 Titel: |
|
|
Die Lösungen sollten bis auf Rundungsfehler stimmen. Den Winkel bei c) würde ich mit negativem Vorzeichen angeben (-18°).
Bitte das nächste Mal vor dem Absenden des Beitrags prüfen, ob der Text korrekt angezeigt wird, das Entziffern ist sonst etwas mühsam.
|
|
|
Nic
Gast
|
| Nic Verfasst am: 29. Sep 2023 17:44 Titel: Re |
|
|
| Myon hat Folgendes geschrieben: | Die Lösungen sollten bis auf Rundungsfehler stimmen. Den Winkel bei c) würde ich mit negativem Vorzeichen angeben (-18°).
Bitte das nächste Mal vor dem Absenden des Beitrags prüfen, ob der Text korrekt angezeigt wird, das Entziffern ist sonst etwas mühsam. |
Sorry, ist mein erster Post. Die Lösungen stimmen, da sie Musterlösungen sind, nur weiß ich nicht, wie ich darauf komme. Auf die Wegstrecke kommt man ja über die Winkelsätze nur wenn ich die Formel F= k * Q/r^2 anwende kommen bei mir andere Ergebnisse raus.
|
|
|
Nic
Gast
|
| Nic Verfasst am: 29. Sep 2023 17:50 Titel: re |
|
|
| Mathefix hat Folgendes geschrieben: | Wo liegt der Schwerpunkt P des gleichseitigen Dreiecks und welchen Abstand r_1, r_2 und r_3 haben die Ecken 1,2,3 vom Schwerpunkt P.
Der Betrag der Feldstärken |E_1|, |E_2| und |E_3| ist umgekehrt proportional zu r^2. |
Der Punkt P liegt im Ursprung, also (0,0,0) . Die Abstände sind folgendermaßen: Abstand zu Q2(0,0.005m,0) Q1(0,0,sqrt(3)/20) und Q3(0.1,0,sqrt(3)/20)
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
| Myon Verfasst am: 01. Okt 2023 11:02 Titel: |
|
|
Bitte entschuldige die so späte Antwort. Ich hatte vorgestern auch einen Satz übersehen und gemeint, es handle sich um Deine Resultate.
Das E-Feld einer Punktladung Q_i am Punkt P ist
=\frac{Q_i}{4\pi\varepsilon_0}\cdot\frac{\vec{r}_P-\vec{r}_{Q_i}}{|\vec{r}_P-\vec{r}_{Q_i}|^3}=-\frac{Q_i}{4\pi\varepsilon_0}\cdot\frac{\vec{r}_{Q_i}}{|\vec{r}_{Q_i}|^3})
Die letzte Gleichung gilt hier, da P im Ursprung liegen soll. Nun ist es eigentlich eine reine Einsetz- und Rechnungsübung.
Die Beträge in a) sollten vergleichsweise einfach zu berechnen sein, wenn der Abstand zum Mittelpunkt bekannt ist (Du kannst z.B. verwenden, dass der Schwerpunkt eines Dreiecks die Seitenhalbierenden im Verhältnis 1:2 teilt).
Zu b). Hier müssen die E-Felder der drei Ladungen als Vektoren addiert werden. Die Komponenten lassen sich auch über den Cosinus bzw. Sinus des Betrages berechnen. Von der Summe dann den Betrag nehmen.
Zu c). Der Winkel ergibt sich aus dem Arcustangens der Komponenten,
)
(Ex ist hier ungleich null).
PS: Deine Koordinaten der Ladungen sind noch nicht ganz richtig. Zur Überprüfung - die Ladungen liegen an den Punkten
, \quad (0, \frac{\sqrt{3}a}{3}), \quad (\frac{a}{2}, -\frac{\sqrt{3}a}{6}))
wobei a die Seitenlänge des Dreiecks ist.
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 05. Okt 2023 17:39 Titel: |
|
|
Die Rechnung ist einfacher in Polarkoordinaten:
Der Radius r ist jeweils von der Dreiecksspitze bis zum Schwerpunkt
(alle drei haben den gleichen Betrag)
Feldstärke
b) und c) Aus der Zeichnung entnehmen wir die Winkel
(E1 < 30°)+(E2 < -90°)+(E3 < -30°) = (110,35 kV/m < 17,78°)
Viele TR können diese winkelgerechte Addition, ansonsten Berechnung mit sin...cos...
Die geringen Abweichungen entstehen wegen der hohen Genauigkeit, mit der der TR arbeitet, z.B. auch bei pi und epsilon0.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
|
|
Registrieren
Login
FAQ
Suchen
