| Autor |
Nachricht |
physicsfirst
Anmeldungsdatum: 19.06.2018
Beiträge: 1
|
 physicsfirst Verfasst am: 19. Jun 2018 13:05 Titel: Seminararbeit - gravitationsfreier Punkt physicsfirst Verfasst am: 19. Jun 2018 13:05 Titel: Seminararbeit - gravitationsfreier Punkt |
 |
|
Meine Frage:
Hallo zusammen,
ich soll für meine Seminararbeit, für die 13te Klasse, einen mathematischen Beweis für einen gravitationsfreien Punkt zwischen 3 Massepunkten führen. Hierzu benötige ich ein Tool mit dem ich die Fläche zwischen den 3 Punkten (Dreiecksfläche) abscannen kann und somit an jedem beliebigen Punkt, in diesem Koordinatensystem, die dort wirkende Kraft auf den Körper zwischen den 3 Punkten bestimmen kann. Mit Geogebra komm ich da leider nicht weit, da ich mit Geogebra keine Kräfte berechnen kann.
Falls zu diesem Problem jemand eine Lösung bzw. Idee hat würde ich mich über Hilfe freuen, Danke!
Meine Ideen:
Bisher verwendet: Geogebra, mathematischer Ansatz FG = FG zwischen allen Punkten und der Versuch das ganze mit dem Taschenrechner zu lösen, würde zwar funktionieren, jedoch würde das viel zu viel Zeit in Anspruch nehmen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 19. Jun 2018 14:10 Titel: Re: Seminararbeit - gravitationsfreier Punkt TomS Verfasst am: 19. Jun 2018 14:10 Titel: Re: Seminararbeit - gravitationsfreier Punkt |
 |
|
| physicsfirst hat Folgendes geschrieben: | | ich soll für meine Seminararbeit, für die 13te Klasse, einen mathematischen Beweis für einen gravitationsfreien Punkt zwischen 3 Massepunkten führen. |
OK
| physicsfirst hat Folgendes geschrieben: | | Hierzu benötige ich ein Tool mit dem ich die Fläche zwischen den 3 Punkten (Dreiecksfläche) abscannen kann und somit an jedem beliebigen Punkt, in diesem Koordinatensystem, die dort wirkende Kraft auf den Körper zwischen den 3 Punkten bestimmen kann. |
Ich denke nicht, dass ein Tool eine mathematischen Beweis liefern kann.
Schreib doch bitte mal den allgemeinen mathematischen Ausdruck für die gesuchte Kraft hin.
Ich habe übriges die Vermutung, dass es hier ein sehr einfaches Argument ohne viel Formeln geben muss.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
physicsfirst.1
Gast
|
 physicsfirst.1 Verfasst am: 20. Jun 2018 13:28 Titel: gravitationsfreier Punkt physicsfirst.1 Verfasst am: 20. Jun 2018 13:28 Titel: gravitationsfreier Punkt |
 |
|
Wir haben 3 Massen, die alle in einer Ebene liegen und somit ein Dreieck bilden. Nun müssen, um einen gravitationsfreien Punkt zwischen diesen 3 unterschiedlich großen Massen zu bestimmen, die Gravitationskräfte aller 3 Massen zusammen 0 ergeben. Heißt FG1 + FG2 + FG3 = 0 = FG4.
Und dieser Punkt null, muss an einem bestimmten Punkt im Koordinatensystem zu finden sein. Jedoch weiß ich nicht wie ich mit einem normalen Rechenprogramm wie Geogebra, diesen Punkt finden soll, da Geogebra nur x,y Koordinaten angibt und keine Kraftpunkte bzw. keine Kräfte an einem bestimmten Punkt.
Mit freundlichen Grüßen. Domi
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 20. Jun 2018 14:36 Titel: TomS Verfasst am: 20. Jun 2018 14:36 Titel: |
 |
|
| physicsfirst.1 hat Folgendes geschrieben: | | Nun müssen, um einen gravitationsfreien Punkt zwischen diesen Massen zu bestimmen, die Gravitationskräfte aller Massen zusammen Null ergeben. |
Ja.
| physicsfirst.1 hat Folgendes geschrieben: | | Jedoch weiß ich nicht wie ich ... diesen Punkt finden soll. |
Musst du auch nicht.
| physicsfirst hat Folgendes geschrieben: | | ich soll ... einen mathematischen Beweis für einen gravitationsfreien Punkt zwischen 3 Massepunkten führen. |
Du musst diesen Punkt nicht explizit finden, du sollst lediglich beweisen, dass er existiert - oder verstehe ich die Aufgabe falsch?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Physicsfirst2
Gast
|
 Physicsfirst2 Verfasst am: 20. Jun 2018 21:25 Titel: Physicsfirst2 Verfasst am: 20. Jun 2018 21:25 Titel: |
 |
|
|
Naja, ganz genau kann man diesen Punkt natürlich nicht nachweisen bzw. berechnen. Aber ich soll ihn halt so nahe wie möglich bestimmen und auch grafisch belegen, wo dieser Punkt in etwa liegt. Ist nicht ganz einfach aber deswegen ist es ja auch eine Seminararbeit 😉😅
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 20. Jun 2018 22:55 Titel: TomS Verfasst am: 20. Jun 2018 22:55 Titel: |
 |
|
Im folgenden eine kurze Beweisskizze für die Existenz eines Gleichgewichtspunktes. Daraus ergibt sich auch sofort die Idee zu einer (numerischen) Lösung.
1) Die Gravitationskraft ist der Gradient eines skalaren Potentials. Die Existenz eines Punktes mit verschwindender Kraft ist äquivalent zur Existenz eines Extremums (oder eines Sattelpunktes) des Potentials.
2) Die Potentialfunktion ist die Summe dreier -1/r Terme. Das Potential ist also sicher überall negativ und hat demnach sicher (mindestens) ein Maximum < 0. Außerdem ist die Potentialfunktion überall stetig und differenzierbar, außer an den drei Polen.
Aus (2) folgt die Existenz eines Maximums, demnach folgt mir (1) die Existenz eines Gleichgewichtspunktes mit verschwindender Kraft; q.e.d.
Das explizite Finden des Gleichgewichtspunktes ist demnach äquivalent zum Finden eines Maximums von

wobei r und r_i jeweils Vektoren bezeichnen.
Die Beweisskizze hat noch eine Lücke; sie lässt zu, dass ein Maximum im Unendlichen liegt - was natürlich der Fall ist - und dass kein weiteres Maximum existiert. Letzteres muss noch ausgeschlossen werden.
EDIT - dazu folgende Beiwesidee: für eine symmetrische Situation mit identischen Massen an den Ecken eines gleichseitigen Dreiecks liegt das Maximum im Mittelpunkt; das ist sehr einfach beweisbar. Nun ist zu zeigen, dass bei einer stetigen Variation der Parameter (r_i, M_i) der Ort des Maximums eine stetige Kurve beschreibt, d.h. dass dieses Maximum nicht verschwindet. Dazu fällt mir sicher auch nich was ein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Jun 2018 08:59, insgesamt einmal bearbeitet |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 21. Jun 2018 09:27 Titel: TomS Verfasst am: 21. Jun 2018 09:27 Titel: |
 |
|
Ich habe zu meiner Idee auch eine Frage im Matheboard formuliert:
Gegeben sei eine Funktion phi(r,a)

Außerdem sei vorausgesetzt, dass für bestimmte Werte von a die Menge E der Extrema und Sattelpunkte von phi exakt bekannt ist:
 = \{r: \, \nabla \, \phi(r,a) = 0 \})
Bei infinitesimaler Variation der Paramater a beschreibt der N-te Wert in E eine infinitesimale Kurve

Für eine infinitesimale Variation kann die Gleichung
 = 0 )
um die bekannte Lösung linearisiert werden.
Frage: welche Eigenschaften muss phi(r,a) haben, so dass man argumentieren kann, dass ein derartiger Punkt N aus E nicht verschwindet, d.h. dass die Kurve C_N keinen Endpunkt hat.
M.E. folgt dies aus Stetigkeit und Regularität; d.h. dass wenn die Orte der Massen sich stetig ändern und z.B. nicht zusammenfallen, die Anzahl der Punkte in E konstant bleibt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Jun 2018 12:31, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
 Myon Verfasst am: 21. Jun 2018 10:51 Titel: Myon Verfasst am: 21. Jun 2018 10:51 Titel: |
 |
|
Könnte man das nicht vielleicht irgendwie so zeigen (meine Mathematik-Vorlesungen liegen schon längere Zeit zurück, ist nur ein Gedankengang..):
Man betrachtet das Dreieck, auf dessen Eckpunkten die drei Massen liegen. Dies ist eine abgeschlossene Menge. Das Potential muss darauf, da es wie oben gezeigt durch 0 nach oben beschränkt ist, ein Maximum annehmen.
Nun muss man noch zeigen, dass das Maximum nicht auf dem Rand, also auf einer Verbindungsstrecke zwischen zwei Massen, liegen kann. Zumindest anschaulich gesehen kann ein Punkt auf dem Rand aber kein Maximum sein, da dort durch die dritte Masse der Gradientenvektor/Kraftvektor auf jeden Fall ins Innere zeigt. Liegt anderseits das Maximum im Innern, so muss dort der Gradient verschwinden.
PS: OK, da besteht noch das Problem der drei Eckpunkte, da dort das Potential nicht definiert ist...
PPS: Bitte um Entschuldigung, auch das obige Argument, dass das Maximum nicht auf dem Rand liegen kann, stimmt nicht, da der Gradient des Felds der dritten Masse nach aussen, nicht nach innen zeigt.
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 21. Jun 2018 12:16 Titel: gnt Verfasst am: 21. Jun 2018 12:16 Titel: |
 |
|
Numerisch ist das doch nicht schwer: Man nimmt das Kraftfeld, also das Vektorfeld f(x,y); davon bildet man die Norm, also norm(f(x,y)). Diese Funktion minimiert man für alle drei Mittelpunkte der Kanten des Dreiecks.
Plotten und berechnen sollte man das alles auf wolframalpha.com können.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 21. Jun 2018 12:46 Titel: Huggy Verfasst am: 21. Jun 2018 12:46 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | Numerisch ist das doch nicht schwer: Man nimmt das Kraftfeld, also das Vektorfeld f(x,y); davon bildet man die Norm, also norm(f(x,y)). Diese Funktion minimiert man für alle drei Mittelpunkte der Kanten des Dreiecks. |
Was hat das mit der Problemstellung zu tun? Nichts!!! Also Quark! 
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 21. Jun 2018 13:52 Titel: Steffen Bühler Verfasst am: 21. Jun 2018 13:52 Titel: |
 |
|
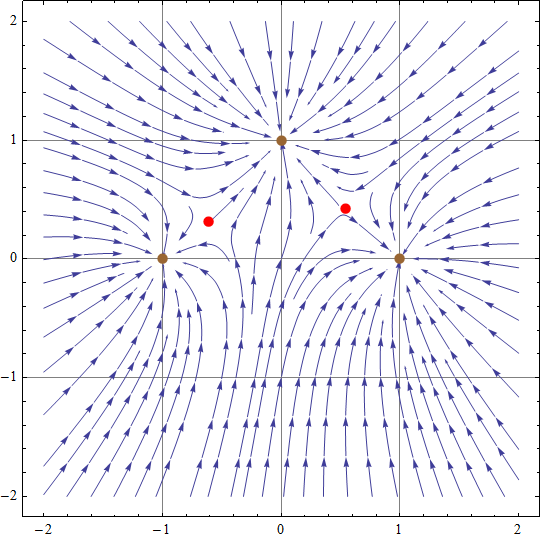
| Huggy hat Folgendes geschrieben: | | Zur Illustration mal ein mit Mathematica erstelltes Feldlinienbild. |
Ansatzweise lässt sich das ja auch mit Geogebra hinkriegen (siehe unten). Die Gleichgewichtspunkte kann man sich dann ausgeben lassen. Unklar ist mir hier nur, warum zwischen m1 und m2 nicht ebenfalls einer ist.
Viele Grüße
Steffen
| Beschreibung: |
|
| Dateigröße: |
45 KB |
| Angeschaut: |
2470 mal |

|
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 21. Jun 2018 14:25 Titel: gnt Verfasst am: 21. Jun 2018 14:25 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | Numerisch ist das doch nicht schwer: Man nimmt das Kraftfeld, also das Vektorfeld f(x,y); davon bildet man die Norm, also norm(f(x,y)). Diese Funktion minimiert man für alle drei Mittelpunkte der Kanten des Dreiecks. |
Was hat das mit der Problemstellung zu tun? Nichts!!! Also Quark!  |
"Quark"? Tatsächlich?
Der Fragesteller hat zwei Anliegen: Zum einen "einen mathematischen Beweis", wobei mir nicht klar ist, was bewiesen werden soll (Die Existenz eines solchen Punktes?) und zum anderen "diesen Punkt finden". Letzteres funktioniert mit meinem Ansatz für diese Punkte ohne viel Mühe, wenn man eine entsprechende Software nutzen kann/darf.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 21. Jun 2018 14:52 Titel: Huggy Verfasst am: 21. Jun 2018 14:52 Titel: |
 |
|
|
Das funktioniert mit deinem Ansatz nicht, weil die Gleichgewichtspunkte nicht auf den Verbindungslinien der Massen liegen und schon gar nicht in deren Mitte. Man muss schon das gesamte Innere des Dreiecks betrachten. Und dann ist eine Nullstellensuche wesentlich effektiver als ein reines Abscannen des Gebiets.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 21. Jun 2018 14:59 Titel: Huggy Verfasst am: 21. Jun 2018 14:59 Titel: |
 |
|
| Steffen Bühler hat Folgendes geschrieben: | | Huggy hat Folgendes geschrieben: | | Zur Illustration mal ein mit Mathematica erstelltes Feldlinienbild. |
Ansatzweise lässt sich das ja auch mit Geogebra hinkriegen (siehe unten). Die Gleichgewichtspunkte kann man sich dann ausgeben lassen. |
Die Möglichkeiten von Geogebra kenne ich nicht. Aber über das Potential sind die Gleichgewichtspunkte schwer zu finden. Sie sind nämlich - jedenfalls in meinem Beispiel - keine lokalen Maxima des Potentials sondern Sattelpunkte. Ich bin über die Kräfte gegangen.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 21. Jun 2018 15:19 Titel: Steffen Bühler Verfasst am: 21. Jun 2018 15:19 Titel: |
 |
|
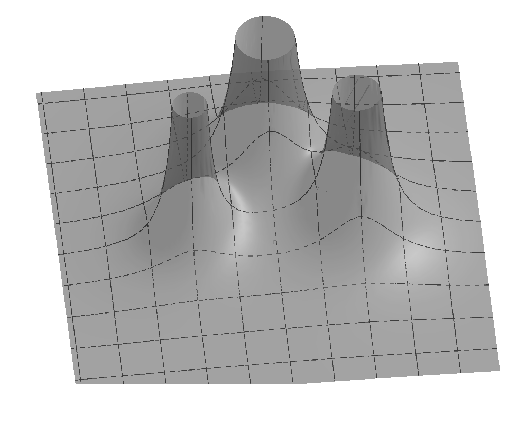
Ich arbeite auch nicht soviel mit Geogebra, aber wenn man etwas in die 3D-Grafik reinzoomt, beantwortet das meine Unklarheit: die beiden von Dir genannten Gleichgewichtspunkte sind Sattelpunkte, auf denen man sozusagen sitzen kann, ohne abzurutschen. Zwischen m1 und m2 dagegen ist es immer "abschüssig".
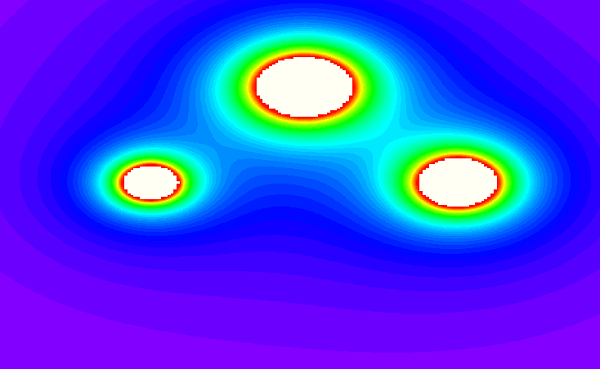
Mit einem anderen Programm lässt sich das Ganze von oben mit Höhenlinien noch klarer darstellen. Ob Geogebra das kann, weiß ich nicht.
Nun müsste man eben nur noch beweisen, dass es immer mindestens einen Sattelpunkt gibt.
| Beschreibung: |
|
| Dateigröße: |
51.64 KB |
| Angeschaut: |
2440 mal |
|
| Beschreibung: |
|
| Dateigröße: |
101.02 KB |
| Angeschaut: |
2441 mal |
|
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 21. Jun 2018 15:42 Titel: gnt Verfasst am: 21. Jun 2018 15:42 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Das funktioniert mit deinem Ansatz nicht, weil die Gleichgewichtspunkte nicht auf den Verbindungslinien der Massen liegen und schon gar nicht in deren Mitte. |
Das habe ich nicht geschrieben.
| Huggy hat Folgendes geschrieben: | | Man muss schon das gesamte Innere des Dreiecks betrachten. |
Mein Ansatz ist "Diese Funktion minimiert man für alle drei Mittelpunkte der Kanten des Dreiecks.", also die Suche nach lokalen Minima um eben diese "drei Mittelpunkte der Kanten".
|
|
 |
Physicsfirst2
Gast
|
 Physicsfirst2 Verfasst am: 21. Jun 2018 16:45 Titel: Physicsfirst2 Verfasst am: 21. Jun 2018 16:45 Titel: |
 |
|
Schon mal danke für die vielen Antworten und Lösungsvorschläge! Analytisch lässt sich dieses Problem zwar lösen, jedoch würde dass ewig dauern da man jeden möglichen Punkt x innerhalb zwischen den 3 Massen berechnen müsste und schauen müsste an welchem Punkt man am nächsten dem Wert Null ist. Das wäre irrsinnig viel Rechenarbeit, von daher meine Idee das womöglich mit einem Programm lösen zu können, welches mir die Kraft, an jedem beliebigen Punkt zwischen diesen 3 Massen, die auf meine Probemasse wirkt anzeigt.
Weiß leider nicht in wiefern das noch verständlich ist. Aber mein Seminarbetreuer hat gemeint es wäre schön wenn man eine Animation hätte, bei der es mir an jedem beliebigen Punkt an den ich klicke, die dort auf meine Probemasse wirkende Kraft sofort anzeigt.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 21. Jun 2018 16:55 Titel: Steffen Bühler Verfasst am: 21. Jun 2018 16:55 Titel: |
 |
|
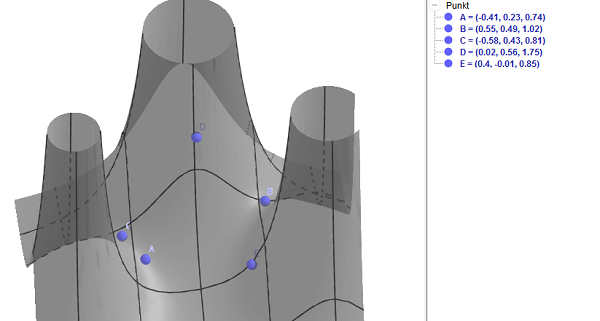
Dann passt ja doch Geogebra! Da kannst Du beliebig viele Punkte in die Grafik setzen oder nur einen Punkt mit der Maus hin- und herschieben, die Koordinaten werden gleich angezeigt.
| Beschreibung: |
|
| Dateigröße: |
59.75 KB |
| Angeschaut: |
2409 mal |
|
|
|
 |
Physicsfirst1.2
Gast
|
 Physicsfirst1.2 Verfasst am: 21. Jun 2018 22:20 Titel: Physicsfirst1.2 Verfasst am: 21. Jun 2018 22:20 Titel: |
 |
|
Alles klar, dann werde ich es nochmal mit Geogebra versuchen, Danke! 😉
Nur die Frage: was muss ich da auswählen um es grafisch so darzustellen wie du es gemacht hast? Also mit den „Hügeln“? Geht das mit Geometrie, 3D Grafikrechner oder welchen?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 22. Jun 2018 08:49 Titel: Steffen Bühler Verfasst am: 22. Jun 2018 08:49 Titel: |
 |
|
Ich hab hier "GeoGebra Classic 5.0.473.0-d (07 June 2018)" und dort die abgebildete Formel eingegeben sowie "Ansicht/3D Grafik" eingeschaltet.
Ich weiß nicht, was Du genau hast, ich hab's auch nur damit versucht, weil Du es offenbar kennst. Jedenfalls kann man damit durchaus weiterkommen.
Die Formel müsste wahrscheinlich noch verbessert werden, ich habe ja nur die Beträge der drei Kräfte addiert. Korrekt wäre es vektoriell, aber das ist ja nicht so schwierig.
Viele Grüße
Steffen
|
|
 |
Physicsfirst1.
Gast
|
 Physicsfirst1. Verfasst am: 22. Jun 2018 11:19 Titel: Physicsfirst1. Verfasst am: 22. Jun 2018 11:19 Titel: |
 |
|
|
Super, funktioniert alles! Danke dir! Absolut hilfreich! 👍🏼😊
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
 Myon Verfasst am: 22. Jun 2018 11:30 Titel: Myon Verfasst am: 22. Jun 2018 11:30 Titel: |
 |
|
|
M.E. wäre es aussagekräftiger, das Potential zu plotten. Bei einem lokalen Minimum des Kraftbetrags muss die Kraft nicht notwendigerweise =0 sein, im Gegensatz zu einem Extremum des Potentials.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 22. Jun 2018 12:24 Titel: TomS Verfasst am: 22. Jun 2018 12:24 Titel: |
 |
|
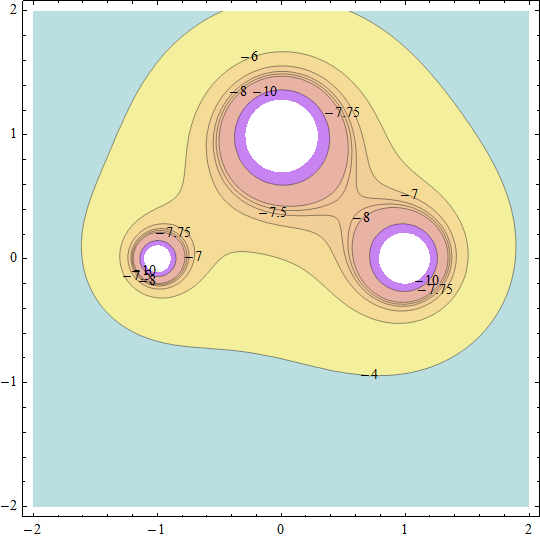
Ich würde das Potential in 2D mit Höhenlinien oder Farbe plotten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Jun 2018 13:00 Titel: Huggy Verfasst am: 22. Jun 2018 13:00 Titel: |
 |
|
Die einzige Stelle, bei der ich bei Steffen Bühler eine Formel sehe, ist sein erstes Bild. Und da steht, mal vom Vorzeichen abgesehen, das Potential.
Bei einer Seminararbeit würde ich mich nicht auf nur eine Darstellung beschränken. Eine Darstellung des Potentials und eine Darstellung der Kraft (oder der Feldlinien) erhöht sicher das Verständnis.
Hier eine Darstellung des Potentials im Sinne von TomS, bei der ich versucht habe, den rechten Gleichgewichtspunkt zu verdeutlichen. Das ist sicher noch verbesserungsfähig.
| Beschreibung: |
|
| Dateigröße: |
50.35 KB |
| Angeschaut: |
2303 mal |
|
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
 Myon Verfasst am: 22. Jun 2018 13:06 Titel: Myon Verfasst am: 22. Jun 2018 13:06 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Die einzige Stelle, bei der ich bei Steffen Bühler eine Formel sehe, ist sein erstes Bild. Und da steht, mal vom Vorzeichen abgesehen, das Potential. |
Nicht ganz, denn im Nenner steht jeweils der Abstand im Quadrat.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Jun 2018 13:11 Titel: Huggy Verfasst am: 22. Jun 2018 13:11 Titel: |
 |
|
Stimmt! 
Das hatte ich übersehen!
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 22. Jun 2018 13:29 Titel: TomS Verfasst am: 22. Jun 2018 13:29 Titel: |
 |
|
Schöne Darstellung.
Drei generelle Anmerkungen:
Ich weiß, der allgemeine Beweisansatz ist noch unfertig, aber den würde nicht aus den Augen verlieren.
Evt. sollte man diskutieren, dass eine statische Anordnung dreier Massen natürlich instabil ist, dass jedoch eine realistische stabile Lösung für drei Massen nicht allgemein berechenbar ist.
Außerdem stellt sich die Situation aufgrund der Bewegung der Massen für eine stabile Lösung nochmals anders dar.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Jun 2018 13:37 Titel: Huggy Verfasst am: 22. Jun 2018 13:37 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Schöne Darstellung.
Ich weiß, der allgemeine Beweisansatz ist noch unfertig, aber den würde nicht aus den Augen verlieren. |
Das findet auch mein Interesse, aber all meine Überlegungen erwiesen sich bisher als lückenhaft.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 22. Jun 2018 13:46 Titel: Steffen Bühler Verfasst am: 22. Jun 2018 13:46 Titel: |
 |
|
|
Solch ein Beweis dürfte auch den Rahmen einer Oberstufen-Seminararbeit sprengen. Eventuell soll der "Beweis" daher nur heuristisch mit einer Mathematiksoftware und verschiedenen Anordnungen dreier Massen geführt werden. Wäre natürlich interessant, die genaue Aufgabenstellung zu kennen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 22. Jun 2018 13:56 Titel: TomS Verfasst am: 22. Jun 2018 13:56 Titel: |
 |
|
Der formale Beweis ist sicher nicht einfach, aber die Argumentation ist generell nachvollziehbar: für eine symmetrische Anordnung existiert ein Gleichgewichtspunkt; für eine sehr kleine Abweichung von der Symmetrie kann jedoch keine große Abweichung vom Potentialverlauf folgen; eine solche wäre jedoch notwendig, um den Gleichgewichtspunkt verschwinden zu lassen; damit ist zumindest klar, dass für nicht zu große Abweichungen von der Symmetrie die Existenz des Gleichgewichtspunktes zwingend gegeben ist (es bleibt zu klären, was “nicht zu groß” quantitativ bedeutet)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
 Myon Verfasst am: 22. Jun 2018 14:05 Titel: Myon Verfasst am: 22. Jun 2018 14:05 Titel: |
 |
|
Unabhängig von der Aufgabenstellung würde mich ein Beweis auch sehr interessieren. Die Idee von TomS mit der stetigen Kurve, die bei der Variation der Massenverhältnisse und Positionen entsteht, finde ich schön. Leider kann ich nichts dazu beitragen... Ich halte es auch für denkbar, dass eine solche Kurve plötzlich endet und ein oder mehrere Gleichgewichtspunkte an anderen Orten entstehen.
Über das Problem müsste es aber doch sicher schon Literatur geben? Wahrscheinlich suche ich nach den falschen Begriffen, aber bisher fand ich nichts dazu.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 22. Jun 2018 14:59 Titel: TomS Verfasst am: 22. Jun 2018 14:59 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Unabhängig von der Aufgabenstellung würde mich ein Beweis auch sehr interessieren. Die Idee von TomS mit der stetigen Kurve, die bei der Variation der Massenverhältnisse und Positionen entsteht, finde ich schön. |
Danke.
| Myon hat Folgendes geschrieben: | | Ich halte es auch für denkbar, dass eine solche Kurve plötzlich endet und ein oder mehrere Gleichgewichtspunkte an anderen Orten entstehen. |
Mit Sicherheit! Einfaches Beispiel:
 = |x|^a)
Es geht ja gerade darum, herauszufinden, unter welchen Bedingungen Gleichgewichtspunkte entstehen bzw. verschwinden, bzw. unter welchen Bedingungen sie erhalten bleiben. Dabei rede ich nicht von diesem konkreten Fall, sondern von einer allgemeinen Formulierung. Im konkreten Fall reden wir ja über ein deformiertes Dreieck aus Massenpunkten. Ein offensichtlich interessanter Fall ist, dass diese drei Massenpunkte in einer Linie liegen.
| Myon hat Folgendes geschrieben: | | Über das Problem müsste es aber doch sicher schon Literatur geben? Wahrscheinlich suche ich nach den falschen Begriffen, aber bisher fand ich nichts dazu. |
So geht’s mir auch :-(
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 22. Jun 2018 23:51 Titel: TomS Verfasst am: 22. Jun 2018 23:51 Titel: |
 |
|
Ich bin ein bisschen weiter gekommen.
Ich verkürze die Notation.
Es geht um

und Lösungen
)
Zunächst führe ich eine (mehrdimensionale) Taylorentwicklung um diese Lösung durch.
 + \nabla_a\phi|_0 (a-a_0) + \frac{1}{2} \begin{pmatrix} r-r_0 \\ a-a_0 \end{pmatrix} \, H|_0 \, \begin{pmatrix} r-r_0 \\ a-a_0 \end{pmatrix} + \ldots )
Die zweiten Ableitungen stecken in der Hesse-Matrix

mit

_{ik} = (\partial_{r_i}\partial_{r_k}\phi)|_0)
sowie

analog.
https://en.m.wikipedia.org/wiki/Hessian_matrix
Im folgenden verschwinden einige Terme:


 = \text{const.} )
 h_{aa} (a-a_0) = \text{const.} )
Es bleibt

Nun geht man wieder zurück zu

und setzt die Taylorentwicklung ein:
 + (\ldots)^t + h_{ra}\,(a-a_0) + (\ldots)^t = 0)
Unter der Voraussetzung, dass die rr-Hesse-Matrix im Minimum invertierbar ist, folgt aufgrund der Symmetrie in rr:
^{-1}[h_{ra}(a-a_0) + (a-a_0) h_{ar}])
Dies bedeutet, dass die infinitesimale Änderung der Lösung für r als Funktion der infinitesimalen Änderung für a in der Hesse-Matrix kodiert ist.
Aus dem o.g. Ausdruck geht hervor, wann eine Parameteränderung am Punkt der Lösung kritisch ist:
1) wenn die rr-Hesse-Matrix dort nicht invertierbar ist.
2) wenn die ar-Hesse-Matrix dort Eigenvektoren zu Eigenwert Null hat
Bisher ist das nur eine grobe Idee. M.E. ist die Problematik komplizierter, z.B. wenn die erste Ableitung bereit singulär wird.
https://en.m.wikipedia.org/wiki/Critical_point_(mathematics)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Jun 2018 11:55 Titel: VeryApe Verfasst am: 23. Jun 2018 11:55 Titel: |
 |
|
Ich habe mich auch mal kurz damit beschäftigt.
Angenommen es gibt einen Punkt 0 innerhalb eines Dreiecks mit den Punkten P1, P2,P3.
Dann entsprechen die Linien von O zu P1, P2, P3 den Radienlinien r1,r2,r3.
Dann könnte ich immer mein Koordinatensystem so ausrichten das die y Achse auf einer der Radienlinie liegt.
Ich habe in der Skizze r3 gewählt.
Siehe Skizze.
Ich erhalte aus


Die Massen sind stehts positiv und seien >0
Die Radien r1,r2 (positiv oder negativ angenommen) ist für die Gleichung irrelevant und deren quadrat ist sowieso stehts positiv.
Nun nehme ich den Winkel  im Quadrant 1 an . im Quadrant 1 an .
daraus folgt das der cosinus von phi positiv ist.
und durch die Gleichung folgt. das der cosinus des Winkel phi,2 negativ sein muß und daher kann er im Quadrant 2 liegen.
alle zwei Winkel können im positiven sinus Bereich liegen.
stellt man die Gleichung für Summe aller Kräfte in y auf, zeigt sich das es immer einen radius r3 gibt, der nach unten auf den Punkt P3 hinführt und dessen Gravitationskraft die Anteile der yKräfte auf r1 und r2 aufhebt.
Damit hätte ich doch mal einen Beweis das es unendliche viele Dreiecke gibt wo es einen Punkt gibt.
Jetzt müsste ich noch beweisen das er in allen Dreiecken existiert.
werd ich mich noch weiter beschäftigen, oder sieht jemand jetzt schon einen Fehler.
| Beschreibung: |
|

Download |
| Dateiname: |
Gravitation Dreieck.GIF |
| Dateigröße: |
29.53 KB |
| Heruntergeladen: |
204 mal |
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Jun 2018 12:42 Titel: index_razor Verfasst am: 23. Jun 2018 12:42 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Ich habe mich auch mal kurz damit beschäftigt.
Angenommen es gibt einen Punkt 0 innerhalb eines Dreiecks mit den Punkten P1, P2,P3.
|
Was soll das bedeuten? Was für ein "Punkt 0" soll hier existieren und warum?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Jun 2018 12:58 Titel: VeryApe Verfasst am: 23. Jun 2018 12:58 Titel: |
 |
|
Sorry angenommen es gibt einen Punkt O im Dreieck bei dem sich alle drei gravitationskräfte aufheben.
Ich muss auch noch überlegen was es bedeutet wenn der cosinus phi 2 grösser als 1 nach der formel ist.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Jun 2018 13:00 Titel: index_razor Verfasst am: 23. Jun 2018 13:00 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Sorry angenommen es gibt einen Punkt O im Dreieck bei dem sich alle drei gravitationskräfte aufheben.
|
Die Existenz so eines Punktes sollst du doch aber zeigen und nicht annehmen.
Worauf soll deine Rechnung denn jetzt hinauslaufen?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18073
|
 TomS Verfasst am: 23. Jun 2018 13:10 Titel: TomS Verfasst am: 23. Jun 2018 13:10 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | VeryApe hat Folgendes geschrieben: | Sorry angenommen es gibt einen Punkt O im Dreieck bei dem sich alle drei gravitationskräfte aufheben.
|
Die Existenz so eines Punktes sollst du doch aber zeigen und nicht annehmen. |
Genau.
Für den symmetrischen Fall ist die Existenz einfach zu beweisen. Kompliziert ist der Beweis, ob und wie daraus auch im nicht-symmetrischen Fall die Existenz folgt.
@index_razor: wäre nett, wenn du meine Ideenskizze kommentieren könntest
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 23. Jun 2018 13:24, insgesamt einmal bearbeitet |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Jun 2018 13:23 Titel: VeryApe Verfasst am: 23. Jun 2018 13:23 Titel: |
 |
|
Ich dachte ich soll zeigen das der Punkt O innerhalb eines Dreieck liegen kann. Die Existenz eines Punktes O ausserhalb des Dreieck ist doch wohl in der Unendlichkeit gegeben.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
|