| Autor |
Nachricht |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 06. Jul 2011 19:46 Titel: pressure Verfasst am: 06. Jul 2011 19:46 Titel: |
 |
|
Kannst du die Grafiken bitte etwas verkleinern ?
Danke
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 00:02 Titel: eierkopf Verfasst am: 07. Jul 2011 00:02 Titel: |
 |
|
Weiß keiner, ob meine Ansätze richtig sind? 
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 01:10 Titel: VeryApe Verfasst am: 07. Jul 2011 01:10 Titel: |
 |
|
zu a) richtig
zu b) verstehe ich nicht, wenn er aufkippt dann kippt er immer weiter.
Am einfachsten löst man das mit der dalembertschen Trägheitskraft.
Das Kraftmoment der Trägheitskraft um Punkt A wird immer größer während das Kraftmomnet der Gewichtskraft immer kleiner wird.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 08:11 Titel: eierkopf Verfasst am: 07. Jul 2011 08:11 Titel: |
 |
|
Vielen Dank fürs Kontrollieren.
Es ist so gemeint:
Der Quader kippt bis zum Winkel  auf, aber dann nicht weiter. auf, aber dann nicht weiter.
| VeryApe hat Folgendes geschrieben: |
zu b) verstehe ich nicht, wenn er aufkippt dann kippt er immer weiter.
Am einfachsten löst man das mit der dalembertschen Trägheitskraft.
Das Kraftmoment der Trägheitskraft um Punkt A wird immer größer während das Kraftmomnet der Gewichtskraft immer kleiner wird. |
Wie mach ich das mit der d'alembertschen Trägheitskraft?
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 08:25 Titel: Packo Verfasst am: 07. Jul 2011 08:25 Titel: |
 |
|
eierkopf,
die Lösung a) ist falsch.
Was VeryApe schreibt ist total falsch!
Rechne nach Newton:
am Körper greifen zwei Kräfte an: die Gravitationskraft m*g und die Auflagerkraft F, die wir in Fx und Fy zerlegen.
(Wenn du schon die Winkelbeschleunigung mit  bezeichnest, dann bitte auch den Winkel mit bezeichnest, dann bitte auch den Winkel mit 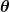 ). ).
Für den Fall b)
betrachte 
bilde
1) Summe aller Kräfte in x-Richtung = m*a
2) Summe aller Kräfte in y-Richtung = 0
3) Kraftmomente um den Schwerpunkt = 
Aus diesen 3 Gleichungen erhälst du dann den Winkel 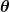 als Funktion von der Beschleunigung a. als Funktion von der Beschleunigung a.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 08:45 Titel: eierkopf Verfasst am: 07. Jul 2011 08:45 Titel: |
 |
|
| Packo hat Folgendes geschrieben: | eierkopf,
die Lösung a) ist falsch.
Was VeryApe schreibt ist total falsch!
Rechne nach Newton:
am Körper greifen zwei Kräfte an: die Gravitationskraft m*g und die Auflagerkraft F, die wir in Fx und Fy zerlegen.
(Wenn du schon die Winkelbeschleunigung mit  bezeichnest, dann bitte auch den Winkel mit bezeichnest, dann bitte auch den Winkel mit 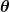 ). ).
|
Da ich die max. Beschleunigung berechnen muss, sollte doch diese Auflagekraft F=0 sein, oder?
Zu b)
1) In x-Richtung sind keine Kräfte vorhanden: ma = 0
2) In y-Richtung ist nur die Gewichtskraft vorhanden: 0 = - m*g
Aber das kann beides nicht sein. Wo liegt mein Fehler? 
Da sich der Schwerpunkt S bewegt, kann ich den Momentensatz doch dort nicht anwenden, da man einen raumfesten Bezugspunkt braucht, oder?
Deswegen habe ich die obige Version des Momentensatz verwendet.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 09:16 Titel: VeryApe Verfasst am: 07. Jul 2011 09:16 Titel: |
 |
|
Die Unterlage bewegt sich nach rechts unter beschleunigung.
Aufgrund der unterlage wirken Zwangskräfte die entweder direkt über die Befestigung von Punkt A oder über die Fläche der Ebene übertragen werden, die den Punkt A mit der Ebene mitschleifen.
Mit Kräften sieht das so aus.
| Beschreibung: |
|

Download |
| Dateiname: |
Kraefte.png |
| Dateigröße: |
14.43 KB |
| Heruntergeladen: |
2752 mal |
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 09:21 Titel: VeryApe Verfasst am: 07. Jul 2011 09:21 Titel: |
 |
|
Ax=m*a0
Ay wandert und zwar wenn a0=0 dann steht es genau unter dem Schwerpunkt
Je höher a0 umso mehr wandert es nach links bis es bei Punkt A ist.. dann hast die maximal Grenze die du berechnest.
Die Trägheitskraft nach Dalembert liefert einen Gleichgewichtsfall.
Man sieht das kein Unterschied wäre ob jetzt die Unterlage nicht beschleunigt wäre und man wirkt einfach im Schwerpunkt mit einer Kraft nach links kommt aufs selbe hinaus.
| Zitat: |
Da sich der Schwerpunkt S bewegt, kann ich den Momentensatz doch dort nicht anwenden, da man einen raumfesten Bezugspunkt braucht, oder?
Deswegen habe ich die obige Version des Momentensatz verwend
|
Den Momentensatz kannsd du um jeden Punkt anwenden, wie in der Statik.
| packo hat Folgendes geschrieben: |
Rechne nach Newton:
am Körper greifen zwei Kräfte an: die Gravitationskraft m*g und die Auflagerkraft F, die wir in Fx und Fy zerlegen.
|
Das ist natürlich richtig, man kann es auch so machen. Nur sollte man es auch richtig ausfürhen, dann kommt man auf die obige Lösung
Wenn der Körper einmal kippt dann kippt er immer weiter.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 09:47 Titel: eierkopf Verfasst am: 07. Jul 2011 09:47 Titel: |
 |
|
Zu a)
a) sollte damit geklärt sein, da ja diese Zwangskräfte Ax und Ay kein Moment bzgl. A besitzen.
Zu b)
Diese Trägheitskraft nach d'Alembert haben wir in der Vorlesung nicht gemacht.
Ich versuchs nochmals:
x-Richtung: 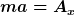
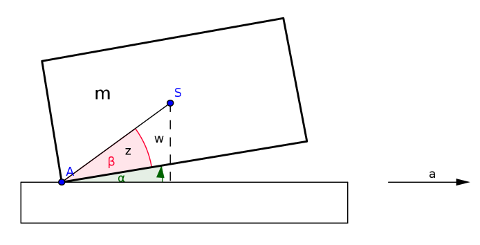
y-Richtung: 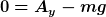
Moment um S:  z - A_y \cos(\alpha+\beta)z)
Jedoch komme ich dann wieder auf das, das ganz oben steht. 
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 09:54 Titel: VeryApe Verfasst am: 07. Jul 2011 09:54 Titel: |
 |
|
Ja weil es egal ist welchen Momentenpunkt du nimmst, du kommst immer aufselbe, jedoch gibts keine Lösung, dann rechne mal den Winkel alpha aus.
Alleine von Kraftverständnis müsstest du doch erkennen das das immer weiter kippt und ab alpha 90 Grad dreht sich die drehrichtung der Schwerkraft, sie wirkt dann nicht mehr dagegen.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 10:10 Titel: eierkopf Verfasst am: 07. Jul 2011 10:10 Titel: |
 |
|
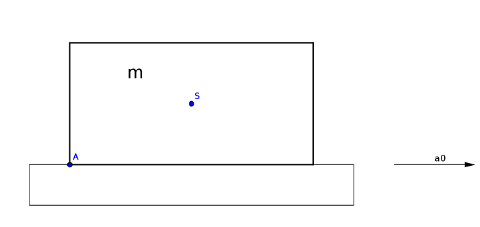
Das war eine Prüfungsaufgabe. Leider habe ich die Angabe nicht mehr. Aber ich glaube, die gegebene Zeichnung war so, dass der Quader höher war als breit.
Der Prof. meinte, dass dieser Winkel  konstant wäre. Die Beschleunigung a darf natürlich kaum größer sein, als die max. Beschleunigung a0 unter a). konstant wäre. Die Beschleunigung a darf natürlich kaum größer sein, als die max. Beschleunigung a0 unter a).
Auf diese Lösung komme ich:

mit
 . .
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 10:19 Titel: VeryApe Verfasst am: 07. Jul 2011 10:19 Titel: |
 |
|
Es ist egal welche Höhe oder Breite der Quader hat.
Wenn er höher ist als breiter dann ist die einzige Lösung er dreht sich auf 90 Grad, sodass er mit der längeren Seite zu Boden liegt
Eine Schrägstellung ist nicht möglich, würd mich mal interessieren was dein Professor da ausgerechnet hat, mit den Vorgaben von dir ist das für mich falsch, vielleicht fragst du den nochmals.
Überleg doch mal selber wie verändern sich die Kraftmomente bezüglich A wenn der Körper sich aufstellen würde.
Das Kraftmoment der Gewichtskraft wird immer kleiner, das Kraftmoment der Trägheistkraft immer größer de rKörper kippt immer schneller gegen den Uhrzeigersinn. ab 90 Grad dreht die Schwerkraft ín die andere Richtung
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 10:24 Titel: VeryApe Verfasst am: 07. Jul 2011 10:24 Titel: |
 |
|
die Einzige Möglichkeit wäre den Körper schrägzustellen.
du lässt eine Beschleunigung größer als a0 Kippgrenze wirken, und reduzierst dann wieder die Beschleunigung unter a0 Kippgrenze. .
aber hier steht doch a0 konstant.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 10:31 Titel: eierkopf Verfasst am: 07. Jul 2011 10:31 Titel: |
 |
|
Die Beschleunigung war sicher konstant.
Dass sich der Körper "überdreht", kommt mir jetzt auch schon immer logischer vor. 
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 10:55 Titel: Packo Verfasst am: 07. Jul 2011 10:55 Titel: |
 |
|
eierkopf,
dein Resultat für a) ist richtig. Da habe ich mich geirrt, weil ich bei dir eine Zeile darüber gelesen habe und die Masse m als Faktor gesehen habe.
Zu deinem Ansatz für b)
Es wirkt doch in x-Richtung die horizontale Komponente der Auflagerkraft im Punkt A. Sonst würde sich der Körper ja überhaupt nicht beschleunigen.
Dies ist die einzige Kraft in horizontaler Richtung.
Stelle die Momentengleichung um den Schwerpunkt auf!
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 10:59 Titel: eierkopf Verfasst am: 07. Jul 2011 10:59 Titel: |
 |
|
| Packo hat Folgendes geschrieben: |
Zu deinem Ansatz für b)
Es wirkt doch in x-Richtung die horizontale Komponente der Auflagerkraft im Punkt A. Sonst würde sich der Körper ja überhaupt nicht beschleunigen.
Dies ist die einzige Kraft in horizontaler Richtung.
Stelle die Momentengleichung um den Schwerpunkt auf! |
Ist das nicht das, was ich oben geschrieben habe:
x-Richtung: 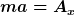
y-Richtung: 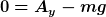
Moment um S:  z - A_y \cos(\alpha+\beta)z)
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 11:19 Titel: Packo Verfasst am: 07. Jul 2011 11:19 Titel: |
 |
|
eierkopf,
jetzt stimmt's in x- und y-Richtung. (Ich war mit meinem Kommentar wohl einige Beiträge von dir im Rückstand).
Zu den Drehmomenten:
nimm als Variable nur den Winkel (meinetwegen alpha).
Drücke die Momente um S mit diesem Winkel und a und b aus!
So erhälst du 3 Gleichungen mit den Unbekannten Ax, Ay, alpha.
Und selbstverständlich gibt es eine Lösung!
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 11:28 Titel: eierkopf Verfasst am: 07. Jul 2011 11:28 Titel: |
 |
|
Zu den Drehmomenten:
Moment um S:  z - A_y \cos(\alpha+\beta)z)
Stimmt das nicht? Habe ich was vergessen?
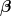 und z sind konstant und diese habe ich schon bestimmt. und z sind konstant und diese habe ich schon bestimmt.
Oder wie meinst du das genau?
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 11:39 Titel: Packo Verfasst am: 07. Jul 2011 11:39 Titel: |
 |
|
eierkopf,
für alpha > 0 gilt:
+1/2*h*cos(\alpha))-Ay*(1/2*b*cos(\alpha)-1/2*h*sin(\alpha))=0)
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 11:54 Titel: eierkopf Verfasst am: 07. Jul 2011 11:54 Titel: |
 |
|
Vielen Dank für die Antwort!
Ich kann deine Gleichung nachvollziehen. Löse ich diese auf  auf, komme ich aber wieder auf das selbe Ergebnis wie oben. Leider ist dieser Winkel auf, komme ich aber wieder auf das selbe Ergebnis wie oben. Leider ist dieser Winkel  negativ. negativ. 
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 12:16 Titel: Packo Verfasst am: 07. Jul 2011 12:16 Titel: |
 |
|
eierkopf,
ich erhalte als Lösung:
)
Ich glaube, du interpretierst das Ergebnis falsch!
Was bedeutet denn dieses Resultat?
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 12:28 Titel: eierkopf Verfasst am: 07. Jul 2011 12:28 Titel: |
 |
|
| Packo hat Folgendes geschrieben: | eierkopf,
ich erhalte als Lösung:
)
Ich glaube, du interpretierst das Ergebnis falsch!
Was bedeutet denn dieses Resultat? |
Der Nenner ist sicher positiv.
Der Zähler ist sicher negativ, da a >a0.
Der Arctan von etwas Negativen ist wieder negativ und damit ist der Winkel negativ.
Der Winkel wird doch gegen den Uhrzeigersinn gezählt. Oder was meinst du?
(Mathematica kommt auf ein kleinwenig anderes Ergebnis.)
Zuletzt bearbeitet von eierkopf am 07. Jul 2011 12:29, insgesamt einmal bearbeitet |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 12:28 Titel: VeryApe Verfasst am: 07. Jul 2011 12:28 Titel: |
 |
|
packo , was du berechnest ist, das ein Körper bei einer bestimmten Beschleunigung die Schrägstellung halten könnte, ohne das er sich verdreht, das bezweifelt ja keiner.
Diese Beschleunigung variiert je nach Schräglage.
Es ist aber gefordert das der Körper mit einer Beschleunigung konstant beschleunigt die ihn aus der Ruhelage umkippt.
Welche Beschleunigung dazu notwendig ist siehe Aufgabenteil a)
Setze das hier ein und betrachte die Lösung.
Man muß übrigens kein Genie sein um zu erkennen das es hier keine Lösung gibt.
Ich würde dir raten weil du dich gut mit Statik auskennst, das du dich in die Dalembertsche Trägheitskraft einarbeitest, diese ist zwar nur begrenzt in Büchern aufgeführt aber mit einigen eigenen Ableitungen kannsd du das umfassend erweitern.
Dann siehst du solche Sachen auf einen Blick ohne das du überhaupt die Mathematik anwenden mußt, alleine durch dein Kraftverständnis aus der Statik.
Das ist nur nebenbei ein Vorschlag
Was der Professor hier ausgerechnet hat verstehe ich nicht. vermutlich stimmen die Vorgaben von eierkopf nicht, aber professoren sind auch nur menschen, dann hat er halt einen Fehler gemacht.
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 12:49 Titel: Packo Verfasst am: 07. Jul 2011 12:49 Titel: |
 |
|
| eierkopf hat Folgendes geschrieben: | Der Zähler ist sicher negativ, da a >a0.
|
Im Ergebnis kommt doch gar kein a0 vor!
Wenn du nicht draufkommst, wie das zu interpretieren ist, erkläre ich es dir gerne.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 13:16 Titel: eierkopf Verfasst am: 07. Jul 2011 13:16 Titel: |
 |
|
| Packo hat Folgendes geschrieben: |
Im Ergebnis kommt doch gar kein a0 vor! |
Ich meinte, dass
 . .
Ja, kannst du mir das bitte erklären.
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 13:44 Titel: Packo Verfasst am: 07. Jul 2011 13:44 Titel: |
 |
|
eierkopf,
wir müssen unterscheiden:
1. Fall: Beschleunigung a < a0 = g*b/h
Der Block bleibt immer in horizontaler Lage.
Wird er angehoben bis zu einem Winkel alpha1 = pi/2-arctan(h/b), so fällt er wieder in die Ausgangslage zurück.
2. Fall: Beschleunigung a > a0 = g*b/h
Es existiert ein Winkel alpha > 0, für den der Block im (labilen) Gleichgewicht ist.
Das heißt: wird der Block um den Winkel < alpha angehoben, so fällt er wieder zurück.
Wird der Block um einen Winkel > alpha angehoben, so kippt er (nach links) um.
Der Grenzwinkel (bei dem Gleichgewicht herrscht), ist also von der Beschleunigung a abhängig. Sein Maximalwert ist
alpha_max= pi/2 - arctan(h/b) für den bei a = 0 Gleichgewicht herrscht.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 13:50 Titel: VeryApe Verfasst am: 07. Jul 2011 13:50 Titel: |
 |
|
| Zitat: | 2. Fall: Beschleunigung a > a0 = g*b/h
Es existiert ein Winkel alpha > 0, für den der Block im (labilen) Gleichgewicht ist.
Das heißt: wird der Block um den Winkel < alpha angehoben, so fällt er wieder zurück.
Wird der Block um einen Winkel > alpha angehoben, so kippt er (nach links) um.
|
Dieser Winkel liegt im 3 Quadranten dazu müsste der block die Ebene durchbrechen und auf der Unterseite liegen.

|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 13:52 Titel: Packo Verfasst am: 07. Jul 2011 13:52 Titel: |
 |
|
Nachtrag zum negativen Winkel alpha:
bei zu kleiner Beschleunigung a, ergibt sich mathematisch ein negativer Winkel, der physikalisch zu ignorieren ist. Der tatsächliche Winkel ist dann = 0.
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 13:54 Titel: Packo Verfasst am: 07. Jul 2011 13:54 Titel: |
 |
|
|
Leider hat der VeryApe es noch immer nicht verstanden!
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 14:54 Titel: VeryApe Verfasst am: 07. Jul 2011 14:54 Titel: |
 |
|
Nein, stimmt ich verstehe nicht was du meinst.
2. Fall: Beschleunigung a > a0 = g*b/h.
Es bildet sich nicht ein labiles sondern ein stabiles Gleichgewicht im 3 . Quadranten.
Für Leute die nicht wissen was der dritte Quadrant ist, das in einem Koordinatensystem mit x (nach rechts ) , y (nach oben positiv )im Bereich -y - x, also links unten.
Der Körper müsste unterhalb der Ebene liegen.
und die Schrägstellung wäre eine stabile Lage.
Jeder veränderung würde die Ausgangsposition der Schrägstellung zurückführen.
Deine Deutungen sind entweder falsch oder man weiß nicht genau was jetzt eigentlich deine aussage ist. ist nun eine Schrägstellung in diesen Fall im oberen Bereich möglich oder nicht?
Wir wollen doch nicht ernsthaft annehmen der Körper durchbräche die Ebene
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 07. Jul 2011 15:07 Titel: VeryApe Verfasst am: 07. Jul 2011 15:07 Titel: |
 |
|
Die einfachste Möglichkeit nach der Physik es zu verstehen.
Wir wechseln ins beschleunigte Bezugssystem von a0
dann wird aufeinmal aus unsere Schwerkraft von m*g eine neue Schwerkraft
NeueSchwerekraft:
 )
Wers dann nicht mehr kapiert, der soll glauben was er will.
Ich habe schon in diesem Thread weiter vorn geschrieben das wenn der Quader höher als breiter ist die einzige Möglichkeit ist, er bleibt mit der längeren Seite liegen. er kippt in die stabilere Lage, aber eine Schrägstellung ist nicht möglich.
|
|
 |
eierkopf
Anmeldungsdatum: 12.03.2011
Beiträge: 17
|
 eierkopf Verfasst am: 07. Jul 2011 18:31 Titel: eierkopf Verfasst am: 07. Jul 2011 18:31 Titel: |
 |
|
Ich habe die Angabe der Prüfung heute nochmals kurz gesehen.
Es steht eher so da:
Beschleunigung 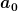 ist konstant. ist konstant.
a) Bestimme die max. Beschleunigung 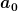 , damit der Quader gerade nicht aufkippt. , damit der Quader gerade nicht aufkippt.
b) Bestimme den Winkel  in Abhängigkeit der Beschleunigung in Abhängigkeit der Beschleunigung  . .
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 07. Jul 2011 18:36 Titel: Packo Verfasst am: 07. Jul 2011 18:36 Titel: |
 |
|
eierkopf,
das habe ich doch gerechnet.
Was willst du denn noch mehr?
Oder hast du es auch nicht verstanden?
|
|
 |
gustav Gans
Gast
|
 gustav Gans Verfasst am: 07. Jul 2011 19:38 Titel: gustav Gans Verfasst am: 07. Jul 2011 19:38 Titel: |
 |
|
|
dann schreibe doch hin der Winkel beträgt 90 Grad egal umwieviel a größer als a0 ist.
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 08. Jul 2011 08:25 Titel: Packo Verfasst am: 08. Jul 2011 08:25 Titel: |
 |
|
gustav Gans,
ich fasse für dich nochmals zusammen:
Der Körper bewegt sich samt Unterlage mit konstanter Beschleunigung a nach rechts. (a ist ein Parameter).
a0 ist jene Beschleunigung, bei der der Körper gerade noch nicht aufkippt.
Wir haben berechnet a0 = g*b/h.
Falls a > a0, so klappt der Körper (um den Punkt A) hoch.
Falls a < a0, so kann man den Körper bis zu einem Winkel alpha1 anheben und er fällt wieder zurück.
Hebt man den Körper um einen Winkel > alpha1 an, so kippt er nach links um.
Bei Anhebung um genau alpha1, befindet sich der Körper im (labilen) Gleichgewicht!
Der Winkel alpha1 hängt von der Beschleunigung a ab. Der Zusammenhang ist:
)
alpha1 wird also umso größer, je kleiner a ist.
Bei einer Beschleunigung a = 0, herrscht Gleichgewicht bei einem Winkel von
)
(aus der geometrischen Betrachtung wenn der Schwerpunkt über dem Punkt A liegt).
Für negative Werte von a, ergibt sich ein symmetrisches Problem.
|
|
 |
gustav Gans
Gast
|
 gustav Gans Verfasst am: 08. Jul 2011 08:59 Titel: gustav Gans Verfasst am: 08. Jul 2011 08:59 Titel: |
 |
|
Vielleicht liest du das nächste Mal die Angaben genauer.
a>a0, wie hier schon mehrfach betont wurde kippt hier alles auf 90 Grad, der Rest von deiner Antworst ist gar nicht gefragt.
Bevor du hier richtige Kommentare als falsch betitelst, überlege lieber dreimal.
|
|
 |
|