| Autor |
Nachricht |
Weizen598
Anmeldungsdatum: 29.01.2022
Beiträge: 23
|
 Weizen598 Verfasst am: 04. Jan 2023 20:03 Titel: Induktion in einer bewegten Leiterschleife |
 |
|
Meine Frage:
Eine kreisförmige Drahtschleife mit Radius R bewegt sich mit konstanter Geschwindigkeit v senkrecht zur Schleifenebene, so dass ihre Lage (unter Vernachlässigung der Drahtdicke) gegeben ist durch  , z=vt. Sie bewegt sich im Feld eines im Ursprung ruhenden magnetischen Dipols  ) . Welche Ringspannung wird in der Schleife induziert, wenn man den Strom in der Schleife vernachlässigt? Skizzieren Sie den Verlauf der Ringspannung. Zu welchem Zeitpunkt wird sie maximal.
Meine Ideen:
Hallo zusammen,
ich habe die Aufgabe jetzt so verstanden, dass sich die Leiterschleife auf der z-Achse immer weiter von dem Dipol entfernt, das B-Feld also immer schwächer wird und dementsprechend eine Spannung induziert wird. Ich wüsste jetzt aber nicht wie ich diese B-Feldänderung berechnen soll. Ich hätte die Aufgabe jetzt ganz klassisch mit  begonnen und die Fläche der Leiterspule, also pi*R^2, eingesetzt, weiter weiß ich aber nicht. Die Skizze und der Zeitpunkt wann die Ringspannung maximal wird sollte kein Problem sein, wenn man die erste Aufgabe gelöst hat.
Ich bedanke mich schonmal im Voraus für jede Hilfe ^^ |
|
 |
Weizen598
Anmeldungsdatum: 29.01.2022
Beiträge: 23
|
| Weizen598 Verfasst am: 05. Jan 2023 22:13 Titel: |
|
|
|
Hat niemand eine Idee? |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3398
|
| ML Verfasst am: 05. Jan 2023 23:49 Titel: |
|
|
Hallo,
| Weizen598 hat Folgendes geschrieben: | | Hat niemand eine Idee? |
Ich würde als erstes nochmal schauen, ob das Dipolmoment zahlenmäßig gegeben ist oder andere vereinfachende Annahmen gegeben sind.
Anschließend brauchst Du die Feldverteilung, die Du hier nachlesen und dann für die Aufgabe verwenden kannst:
https://de.wikipedia.org/wiki/Magnetisches_Dipolmoment#Magnetisches_Feld_eines_magnetischen_Dipols
Das 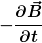 ist bei Dir gleich null, da der Dipol ruht und Du die Schleife bewegst. Deinen Ansatz kannst Du also nicht ohne weiteres nutzen, denn Du hast Dich (ohne es zu merken) in das Ruhesystem der Schleife, aber nicht in das vorgegebene Laborsystem begeben.
In einem bewegten Metallstück herrscht (bei Vernachlässigung des fliießenden Stromes) ein E-Feld von 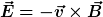 , das Du entlang der Schleife integrieren könntest.
Ich vermute, die Aufgabe ist hässlich zu rechnen, aber noch machbar.
Viele Grüße
Michael |
|
|
Georg Forster
Gast
|
| Georg Forster Verfasst am: 06. Jan 2023 11:06 Titel: |
|
|
| ML hat Folgendes geschrieben: |
Das 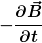ist bei Dir gleich null, da der Dipol ruht und Du die Schleife bewegst. Deinen Ansatz kannst Du also nicht ohne weiteres nutzen, denn Du hast Dich (ohne es zu merken) in das Ruhesystem der Schleife, aber nicht in das vorgegebene Laborsystem begeben.
In einem bewegten Metallstück herrscht (bei Vernachlässigung des fliießenden Stromes) ein E-Feld von 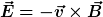, das Du entlang der Schleife integrieren könntest.
Michael |
Machst Du hier nicht denselben Fehler? Im Laborsystem gibt es kein elektrisches Feld. |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3398
|
| ML Verfasst am: 06. Jan 2023 16:26 Titel: |
|
|
Hallo,
| Georg Forster hat Folgendes geschrieben: |
Machst Du hier nicht denselben Fehler? Im Laborsystem gibt es kein elektrisches Feld. |
Im Ausgangszustand (ohne Bewegung) stimmt das.
Das elektrische Feld entsteht erst mit der Bewegung des Leiters im B-Feld.
Viele Grüße
Michael |
|
|
Georg Forster
Gast
|
| Georg Forster Verfasst am: 06. Jan 2023 19:44 Titel: |
|
|
|
Dadurch, dass sich ein Körper im Magnetfeld bewegt, ensteht doch noch kein elektrisches Feld im Laborsystem. Und die Leitfähigkeit des Materials geht in Deine Formel gar nicht ein. |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3398
|
| ML Verfasst am: 06. Jan 2023 21:21 Titel: |
|
|
Hallo,
| Georg Forster hat Folgendes geschrieben: | | Dadurch, dass sich ein Körper im Magnetfeld bewegt, ensteht doch noch kein elektrisches Feld im Laborsystem. Und die Leitfähigkeit des Materials geht in Deine Formel gar nicht ein. |
Wenn Du hier
https://de.wikipedia.org/wiki/Elektromagnetische_Induktion#Beispiel:_Induktion_durch_Bewegung_des_Leiters
mal reinschaust, siehst Du, dass das E-Feld zwischen der oberen und unteren Schiene von der Bewegung des Leiterstabs im Magnetfeld stammt.
Dieses E-Feld ist im Laborsystem vorhanden, im Eigensystem des (bewegten) Leiterstabes jedoch nicht.
In diesem Beispiel ist der Stromkreis nicht geschlossen. Sobald im Stromkreis ein nennenswerter Strom fließt, gilt die Ursprungsannahme, dass B=konstant ist, nur noch näherungsnweise.
Viele Grüße
Michael |
|
|
Georg Forster
Gast
|
| Georg Forster Verfasst am: 07. Jan 2023 11:07 Titel: |
|
|
Ich glaube, ich verstehe jetzt was Du meinst: Im Inneren eines bewegten Leiter gilt das ohmsche Gesetz
) .
Ist die Stromdichte dort 0, so folgt
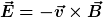
unabhängig von der Leitfähigkeit.
Ich denke aber, dass die Vorgabe, man solle den induzierten Strom vernachlässigen, nicht bedeutet, dass man annehmen solle, es existierte ein elektrisches Wirbelfeld, das den Induktionsstrom verhindert, sondern nur, dass die Leitfähigkeit so klein ist, dass die durch den Induktionsstrom erzeugte Änderung des Magnetfeldes sehr viel kleiner ist als das ursprüngliche Magnetfeld.
Wie dem auch sei. Für die Lösung des Aufgabe muss man jedenfalls das Kurvenintegral über
berechnen. In welchem Zusammenhang diese Größe mit dem elektrischen Feld steht, spielt keine Rolle. |
|
|
|
Registrieren
Login
FAQ
Suchen
