| Autor |
Nachricht |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
|
 |
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
 Ricky Verfasst am: 13. Okt 2010 18:31 Titel: |
 |
|
und warum fällt auf einmal das ² bei ²}{6}) weg... 
|
|
|
PhyMaLehrer
Gast
|
| PhyMaLehrer Verfasst am: 13. Okt 2010 18:56 Titel: |
|
|
Es stimmt tatsächlich! Die Umformung ist natürlich ein bißchen trickreich, denn das Ziel soll ja sein, daß das Ergebnis die gleiche Form hat wie die Ausgangsgleichung am Anfang, nur daß jetzt statt n immer (n+1) dasteht. (Dies ist ja gerade der "Trick" der Induktion, der Schluß von n auf n+1.)
Zunächst wurde der Term (n+1)² in einen Bruch verwandelt, indem er mit 6/6 erweitert wurde. Dadurch können die beiden Brüche mit dem Nenner 6 addiert werden.
*** Da dieser Nenner bis zum Schluß unverändert bleibt, betrachte ich im folgenden nur noch den Zähler des Bruches! ***
Es ist jetzt ein kleiner Schritt weggelassen worden, nämlich daß 6*(n+1)² = 6*(n+1)*(n+1) ist.
Damit wird der Zähler n*(n+1)*(2n+1) + 6*(n+1)*(n+1).
In beiden Summanden ist der Faktor (n+1) enthalten, der ausgeklammert wird. Damit kommt man zum Anfang der 2. Zeile des Induktionsschlusses. Die Klammern im rechten Teil wurden ausmultipliziert, das ergibt die (2n²+n+6n+6), was (2n²+7n+6) ist.
Ein kluger Mensch hat nun herausgefunden, daß man diesen Term schreiben kann als (n+2)*(2n+3) und die (2n+3) sind (2*(n+1)+1).
Wenn man nun das Ergebnis mit der Ausgangsgleichung vergleicht, erkennt man tatsächlich die Ähnlichkeit, wobei n durch n+1 ersetzt wurde.
Puuuhhh...
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 13. Okt 2010 22:01 Titel: |
|
|
Ok vielen lieben Dank.
Du hast es wirklich sehr schön, gut und verständlich erklärt.
Ich habe es nun verstanden. Vielen dank nochmals 
P.S. obwohl ich die ähnlichkeit zur ausgangsgleichung noch nicht so ganz
feststellen konnte... 
|
|
|
PhyMaLehrer
Gast
|
| PhyMaLehrer Verfasst am: 13. Okt 2010 22:09 Titel: |
|
|
Gern geschehen!
Und zur Ähnlichkeit:
Wo oben in der Ausgangsgleichung n steht, steht im Ergebnis (n+1)
oben: (n+1), unten: (n+2), entstanden aus ([n+1]+1)
oben: (2n+1), unten 2*(n+1)+1,
also immer n ersetzt durch (n+1).
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 17:16 Titel: |
|
|
Ja, stimmt. Nun habe ich die Ähnlichkeit auch gesehen. Danke nochmals!
Ich habe allerdings noch eine kleine Aufgabe zur vollständigen Induktion
bei der du (oder jemand anderes hier) vielleicht helfen könnte.
Also:
Wo ist der logische Fehler im folgenden Beweis, dass in jeder Herde von
n Pferden alle Pferde die gleiche Farbe haben?
Induktionsanfang : Für n=1 ist die Behauptung klar
Induktionsschritt von n nach n + 1 : Sei H eine Herde von n + 1 Pferden. Wir nehmen aus H das erste Pferd a heraus und erhalten eine Herde H' von n Pferden, die nach Induktionsvoraussetzung gleichfarbig ist. Wir müssen nur noch zeigen, dass auch a die gleiche Farbe hat. Dazu nehmen wir aus H ein anderes Pferd b heraus und erhalten eine Herde'' von n Pferden, zu der a gehört, und die wieder nach Induktionsvoraussetzung gleichfarbig ist. Sei nun c ein anderes Pferd aus H''. Es hat die gleiche Farbe wie a (da es zu H'' gehört), und auch die gleiche Farbe wie b (da es auch zu H' gehört). Also hat auch a die gleiche Farbe wie b, und somit sind alle n + 1 Pferde aus der Herde H gleichfarbig.
Es wäre wirklich sehr nett, wenn mir jemand dabei helfen könnte...
vielen lieben Dank
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 17:33 Titel: |
|
|
|
Tipp: Der Induktionsschritt ist von n=1 auf n=2 nicht gültig.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 17:41 Titel: |
|
|
das verstehe ich nicht....
also beim durchlesen klingt der beweis doch logisch
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 17:47 Titel: |
|
|
|
Ja, bis auf die Tatsache, dass der Induktionsschritt auf den der Beweis aufbaut, nicht beim Übergang von einem Pferd auf zwei Pferde funktioniert: Hier existiert kein drittes Pferd c. Sodass die Behauptung nicht für n=2 folgt. Somit ist sie auch für alle weiteren Herden mit mehr als zwei Tieren ungültig.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 18:02 Titel: |
|
|
sorry das habe ich noch nicht so ganz verstanden. könntest du es mir
vielleich noch einmal etwas verständlicher und vielleicht anschaulicher
erklären...
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 18:16 Titel: |
|
|
Probier doch mal den Induktionsschritt, so wie er da steht selber von n=1 auf n=2 explizit anzuwenden, bzw. ausformulieren !
Wenn du das gemacht hast. können wir gerne weiter diskutieren, warum dieser Schritt nicht funktioniert.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 18:23 Titel: |
|
|
sorry aber ich verstehe irgendwie gar nicht, was du nun von mir
willst. wie soll ich das denn anwenden. es gibt doch gar keine gleichung
so wie z.B. die gleichung hier aus meinem ersten beitrag wo ich eine
induktion zu anwenden könnte...?
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 18:33 Titel: |
|
|
Entweder bist du zu faul um selber zu denken oder ziemlich schwer von Begriff...
Wozu brauchst du den bitte eine Gleichung ? Die gesamte Aufgabe und der vorgeschlagene Beweis kommen doch auch ohne eine Gleichung aus.
Du sollst mit Hilfe des in der Aufgabe beschrieben Induktionsschrittes, die Behauptung "In einer Herde haben alle Pferde die gleiche Farbe" von einer Herde aus einem Pferd (bei der die Behauptung gültig ist) auf eine Herde von zwei Pferden bestätigen.
Du hast also nun (n=2) Pferde. Das eine Pferd ist Pferd a, das andere Pferd ist Pferd b. Und nimmst du Pferd a aus der Herde raus, sodass für die restliche Herde H', die Behauptung gültig ist... usw.
Wie in der Aufgabenstellung beschrieben nur halt explizit für eine Herde aus zwei Pferden.
Funktioniert es ?
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 19:14 Titel: |
|
|
also ich weiss ja nun, dass der beweis falsch ist.
meine erklärung wäre die, dass man das erste pferd nicht aus der herde
nehmen darf, um den beweis zu liefern. denn wenn man sich den induktionsvorgang wie ein dominoeffekt vorstellt, dann stößt der erste stein ja den zweiten um und bringt das system zum laufen (bzw. zum fallen) und da kann man ja nicht einfach den ersten stein aus dem system nehmen, da dann der zweite stein nicht umfallen würde...oder ist meine
erklärung falsch...
hast du vielleicht noch eine einleuchtendere erklärung...
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 19:32 Titel: |
|
|
Ja dein Idee ist falsch. Den eigentlichen Grund habe ich dir schon gesagt, lies doch einfach was ich geschrieben habe, und oder Versuch die Aufgabe, die ich dir gegeben habe, zu beantworten !
Nochmal in anderen Worten: Für den Induktionsschluss benötigt es mindestens 3 Pferde in der Herde H (Warum ?). Ist der Induktionsschluss damit von n=1 auf n=2 gültig ? Was folgt daraus ?
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 19:50 Titel: |
|
|
wieso benötigt man den mindestens drei pferde...denn wenn man zwei
miteinander vergleicht und die haben dieselbe farbe dann reicht das doch
oder...
und wieso der induktionsschluss von n=1 auf n=2 nicht gültig sein soll
verstehe ich nicht...
Ich weiss ja noch nicht einmal genau was du mit "induktionsschluss von
n=1 auf n=2" meinst...
Sorry, aber ich bin wirklich schon total verzweifelt und brauche dich,
damit du es mir (idiotensicher) erklärst...bitte...
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 20:00 Titel: |
|
|
ich glaube jetzt habe ich es verstanden. ich habe mir gerade nochmal etwas zur vollständigen induktion durchgelesen.
also ich versuche es mal :
der induktionsanfang ist bewiesen, weil bei einer menge von einem pferd ja kein anderes da sein kann, was eine andere farbe hat.
der induktionsschluss hingegen kann nicht bewiesen werden, weil dort
nachgewiesen werden soll, dass man aus der Aussage für eine beliebige
natürliche Zahl n auf die Gültigkeit der Aussage für die nächste Zahl
n+1 schließen kann. das ist jedoch nicht gegeben. denn wenn man für die natürliche zahl n eine konkrete zahl wählt (wie z.B. beim induktionsanfang die zahl 1) dann wird daraus ja nicht unmittelbar bewiesen, dass die aussage für die nächste zahl n+1 gültig ist, da das zweite pferd ja eine andere farbe haben kann...
ist das nun richtig...
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 20:44 Titel: |
|
|
| Zitat: | der induktionsschluss hingegen kann nicht bewiesen werden, weil dort
nachgewiesen werden soll, dass man aus der Aussage für eine beliebige
natürliche Zahl n auf die Gültigkeit der Aussage für die nächste Zahl
n+1 schließen kann. das ist jedoch nicht gegeben. |
Eigentlich ist er schon gegeben, bis auf eine Ausnahme: Der Schritt von 1 auf 2: Weil hier nur zwei Pferde vorhanden sind. Damit fehlt aber das Pferd c, also ist dieser eine Induktionsschritt nicht möglich. Wäre die Aussage, warum auch immer, für 2 Pferde richtig. Würde der Induktionsschritt oder -schluss die Gültigkeit für jede beliebige Zahl liefern.
Ich weiß nicht wirklich, wie ich es dir noch anders erklären soll.
| Zitat: | | Induktionsschritt von n nach n + 1 : Sei H eine Herde von n + 1 Pferden. Wir nehmen aus H das erste Pferd a heraus und erhalten eine Herde H' von n Pferden, die nach Induktionsvoraussetzung gleichfarbig ist. Wir müssen nur noch zeigen, dass auch a die gleiche Farbe hat. Dazu nehmen wir aus H ein anderes Pferd b heraus und erhalten eine Herde'' von n Pferden, zu der a gehört, und die wieder nach Induktionsvoraussetzung gleichfarbig ist. Sei nun c ein anderes Pferd aus H''. Es hat die gleiche Farbe wie a (da es zu H'' gehört), und auch die gleiche Farbe wie b (da es auch zu H' gehört). Also hat auch a die gleiche Farbe wie b, und somit sind alle n + 1 Pferde aus der Herde H gleichfarbig. |
Für diesen Schritt muss n+1 > 2 sein, da es mindestens drei Pferde a,b, und c braucht. Damit ist dieser Schritt aber nicht für 1 auf 2 gültig. Also folgt kein Induktionsschluss aus dem Induktionsanfang.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 21:05 Titel: |
|
|
aber das verstehe ich nicht. denn du schreibst, dass kein induktionsschluss
aus dem anfang folgen kann, weil hier von drei pferden die rede ist.
aber der induktionsbeweis bezieht sich doch allgemein immer auf
eine unendliche menge und die kann man doch dann immer auf
den anfang zurück führen...warum ist das hier nicht so...es
spielt doch keine rolle ob es 3 elemente (3 pferde) oder unendlich viele
sind...
wo ist mein denkfehler
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 14. Okt 2010 21:19 Titel: |
|
|
Induktion beruht doch darauf, dass du von n=1 auf n=2, dann von n=2 auf n=3, dann von n=3 auf n=4 usw. schließen kannst. Allgemein, dann von n auf n+1.
In diesem Beweis funktioniert jeder Schritt: von n=2 auf n=3, von n=3 auf n=4 usw. Nur der Schritt von n=1 auf n=2 funktioniert nicht: Weil in dem Schritt, so wie er hier formuliert wurde, von n auf n+1 mindestens n=2 sein muss, da eben drei Pferde benötigt werden: a, b und c. Dies ist aber von n=1 auf n=2 nicht gegeben. Also bricht die Induktion nach dem Induktionsanfang zusammen: Es fehlt der Schritt von n=1 auf n=2. Und damit sind alle anderen Schritt danach von 2 auf 3 usw. nicht mehr von Belang, da sie mit dem Induktionsanfang nicht verbunden sind.
Das ist jetzt erst mal meine letzte Antwort. Lies dir alles nochmal nach. Solltest du es dann immer noch nicht verstehen, dann kann ich dir auch nicht mehr helfen. Vielleicht will sich ja jmd. anders versuchen. Aber ich sehe keine Möglichkeit mehr: Es steht alles mehrfach da.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 14. Okt 2010 22:04 Titel: |
|
|
ok. vielen lieben dank nochmals. ich denke und hoffe es nun besser verstanden zu haben.
also ich versuche es nochmal mit meinen worten.
da für den beweis der aussage 3 pferde herangezogen wurden wird die
zusatzbedingung n>2 für den schritt von n=2 auf n=3 gestellt.
Der Induktionsschritt verlangt ja den Beweis der Aussage:
Ist A(n) für ein n element der natürlichen Zahlen wahr, dann ist auch A(n+1) wahr.
In dieser beweisführung lautet der beweis der aussage jedoch :
Ist A(n) für ein n element der natürlichen Zahlen und n> 2 wahr, dann ist auch A(n+1) wahr.
somit leistet der angegebene beweis den induktionsschritt nicht,
da die Zusatzbedingung n > 2 gestellt wird.
Der Induktionsanfang müsste somit bei A(2) liegen.
Für diese Behauptung schafft man es allerdings nicht, den Induktionsanfang nachzuweisen, da es ja tatsächlich zwei Pferde mit verschiedenen Farben gibt.
habe ich es nun richtig verstanden...
|
|
|
PhyMaLehrer
Gast
|
| PhyMaLehrer Verfasst am: 15. Okt 2010 09:24 Titel: |
|
|
Ich habe das Problem mit der zweiten Aufgabe erst jetzt gelesen und muß sagen, auch ein (dies vor langer Zeit und auch nur relativ kurz gewesener) PhyMaLehrer ist manchmal mit Blindheit geschlagen, denn ich habe die Erklärung auch nicht verstanden...
Das lag an zwei Dingen: Erstens habe ich die Aufgabe selbst nicht aufmerksam genug gelesen und zweitens habe ich versucht, alles nur im Kopf zu erledigen. Nachdem ich mir die Mengen aufgeschrieben hatte, war aber alles klar.
Meine Erklärung ist folgende:
n=1, Pferd a: Dies hat natürlich "dieselbe Farbe".
Behauptung: n Pferde haben dieselbe Farbe
Jetzt nehmen wir uns eine Menge H mit n+1 Pferden - mindestens drei, es können aber auch mehr sein, dafür stehen die drei Punkte.
H = {a; b; c; ...}
Das uns schon bekannte Pferd a nehmen wir aus H heraus und erhalten damit die Menge
H' = {b; c; ...}
Laut Behauptung haben alle Pferde in H' dieselbe Farbe.
Jetzt lassen wir a wieder in H' zurück und nehmen dafür b heraus:
H" = {a; c; ...}
Laut Behauptung haben auch alle Pferde in H" dieselbe Farbe.
Da das Pferd c (das ja zwischenzeitlich seine Farbe nicht wechselt) sowohl Element von H' als auch von H" ist, haben also alle Pferde von H' und H" (das ergibt die Menge H!) dieselbe Farbe. Also haben tatsächlich alle Pferde dieselbe Farbe.
Wie man sieht, braucht man für den "Beweis" neben a und b unbedingt das Pferd c - und das haben wir in einer Herde von nur zwei Pferden nicht. Für n=2 kann der Beweis also nicht geführt werden. 
Man kann sich aber auch nicht damit retten, die Induktion erst mit n=2 anfangen. Bei n=1 konnte man sagen, daß 1 Pferd immer "dieselbe Farbe" hat. Bei zweien stimmt das aber nicht mehr immer. Also ist damit alles hinfällig!
Ich glaube, jetzt haben wir es beide verstanden! 
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 15. Okt 2010 09:43 Titel: |
|
|
|
Ja, das habt ihr.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 15. Okt 2010 12:45 Titel: |
|
|
vielen lieben dank an euch beide
@PhyMaLehrer : Schade, dass du nun kein Lehrer mehr bist. Denn bei dir
hat bestimmt jeder Schüler sofort alles auf anhieb verstanden. Also bei
deinen erklärungen verstehe ich es zumindest auf jeden Fall immer sofort.
Kompliment! ; ) Und natürlich vielen Dank !
Aber natürlich auch vielen Dank an pressure, denn du hast dir auch alle
mühe gemacht mir die sachlage verständlich zu machen.
P.S. wäre es dann also richtig zu sagen, wenn man den beweis nicht für
a,b,c pferde laut aufgabenstellung führen möchte, sondern nur für a,b
pferde, dass der beweis dann gelingen würde...
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 15. Okt 2010 15:57 Titel: |
|
|
Und wenn wir schonmal dabei sind könnte ich ja vielleicht nochmal bei
folgender aufgabe um eure hilfe bitten...
Also : Zeige mittels vollständiger Induktion, dass für alle natürlichen Zahlen n > 2 gilt :
So und nun bin ich soweit gekommen :
Induktionsanfang :
Linke Seite : 
Rechte Seite : 
Induktionsvoraussetzung :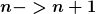 
Induktionsschluss : ²}=2-\frac{1}{n}+\frac{1}{(n+1)²})
so und weiter bin ich nun nicht gekommen...denn das Ziel soll ja für die rechte seite lauten :
weil doch n einfach nur durch n+1 ersetzt werden soll...richtig...
aber irgendwie komme ich mit meiner rechnung dann nicht weiter, sodass ich auf das ziel komme...
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 16. Okt 2010 18:02 Titel: |
|
|
|
hallo, seid ihr noch da, um mir zu helfen...?
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 16. Okt 2010 18:16 Titel: |
|
|
Induktionsanfang ist schon mal falsch: Wenn du es für n > 2 zeigen sollst, dann musst mit n=3 anfangen. Zumal für n=1 diese Bedingung auch nicht erfüllt ist, deswegen fängt es ja erst bei drei an.
Zum Induktionsschritt:
Bis hierhin ist es richtig
²})
Dann darf allerdings kein "=" mehr folgen, sondern:
²}<2-\frac{1}{n}+\frac{1}{(n+1)²})
Jetzt würde ich vorschlagen, dass du dich eines alten Mathematikertricks bedienst und 0 addierst, in diesem Fall:
Anschließend musst du es so ordnen, dass die benötigte Form entsteht + einen Restterm. Wenn du dann zeigen kannst, dass dieser Restterm kleiner als Null ist, dann hast du die Aufgabe gelöst.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 16. Okt 2010 19:30 Titel: |
|
|
Also wenn der Ind.-Anfang bei 3 beginnen soll, dann würde da ja stehen:
Linke Seite : 
und das wäre doch falsch..?
Und dann verstehe ich gar nicht wie du nun auf folgenden term
gekommen bist...
Und ich verstehe auch nicht, wie ich nun weiter vorgehen soll...also was du damit meinst :
| Zitat: | | Anschließend musst du es so ordnen, dass die benötigte Form entsteht + einen Restterm. Wenn du dann zeigen kannst, dass dieser Restterm kleiner als Null ist, dann hast du die Aufgabe gelöst. |
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 16. Okt 2010 19:58 Titel: |
|
|
| Ricky hat Folgendes geschrieben: | Also wenn der Ind.-Anfang bei 3 beginnen soll, dann würde da ja stehen:
Linke Seite :
und das wäre doch falsch..?
|
Ja, das wäre falsch. Es muss ja auch da stehen:
| Ricky hat Folgendes geschrieben: | Und dann verstehe ich gar nicht wie du nun auf folgenden term
gekommen bist...
|
Du willst doch irgendwann auf:
kommen. Die 2 ist vorhanden, aber du brauchst ein  . Da, wie du schon gemerkt hast, man nicht einfach durch herumrechnen auf diesen Term kommst, musst du ihn künstlich erzeugen indem du ihn und seinen negativen Wert addierst, also eigentlich addierst du 0 (deswegen darfst du das überhaupt).
| Ricky hat Folgendes geschrieben: | | Und ich verstehe auch nicht, wie ich nun weiter vorgehen soll...also was du damit meinst : |
²}<2-\frac{1}{n}+\frac{1}{(n+1)²} =2-\frac{1}{n}+\frac{1}{(n+1)²} -\frac{1}{n+1}+\frac{1}{n+1} = 2-\frac{1}{n+1} + \underbrace{\left(-\frac{1}{n}+\frac{1}{(n+1)²}+\frac{1}{n+1}\right)}_{<0 ?} )
Wenn du das was ich unterklammert habe zeigen kannst, dann folgt:
Und du bist fertig.
Abschließend: Du hast die Aufgaben bekommen um sie eigentlich selber zu bearbeiten. Wenn du einen kleinen Denkanstoß brauchst um weiter zu kommen, dann ist das in Ordnung. Aber überhaupt keine Eigeninitiative zu zeigen und immer "ich verstehe nicht,..." zu schreiben bist du die vollständige Lösung hast, ergo gar nicht mehr denken musst, ist nicht in Ordnung. Denk mal darüber nach... wie sollst du was lernen, wenn du alles vorgekaut bekommst.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 16. Okt 2010 20:13 Titel: |
|
|
Also muss der Induktionsanfang dann so lauten...:
Der Rest wäre dann soweit klar. Nur leuchtet mir nicht so recht ein, warum
ich zeigen muss, dass der Term <0 ist. Denn dass der Term <0 ist
bedeutet doch nicht unbedingt, dass der komplette Term dann wegfällt
und nur noch der Rest also übrig bleibt...?
Und wie soll ich das zeigen, dazu müsste ich doch konkrete Zahlen für n
einsetzten können...?
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 16. Okt 2010 20:30 Titel: |
|
|
| Ricky hat Folgendes geschrieben: | Also muss der Induktionsanfang dann so lauten...:
|
Nein - absolut falsch ! Schreib die richtig Summe doch bitte mal aus.
| Ricky hat Folgendes geschrieben: | Der Rest wäre dann soweit klar. Nur leuchtet mir nicht so recht ein, warum
ich zeigen muss, dass der Term <0 ist. Denn dass der Term <0 ist
bedeutet doch nicht unbedingt, dass der komplette Term dann wegfällt
und nur noch der Rest also übrig bleibt...?
Und wie soll ich das zeigen, dazu müsste ich doch konkrete Zahlen für n
einsetzten können...? |
Nirgendwo ist die die Rede von einem "=", so dass du den Term einfach weglassen kannst. Wenn dieser Term aber negativ ist, denn verkleinert er den gesamten Ausdruck, wenn er also weggelassen wird, dann ist der Rest immer größer als der gesamter Ausdruck: Alter Term < Neuer Term (der Rest)
Und nein du darfst für n keine konkreten Zahlen einsetzten, lediglich benutzen, dass es eine natürliche Zahl ist. Rechne doch erst mal mit diesem Term weiter z.B. in dem du ihn auf einen Nenner bringst.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 16. Okt 2010 20:39 Titel: |
|
|
Ist der Ind.-Anfang so richtig...
Und könntest du mir bitte den zweiten teil mit <0 nochmal erklären...ich verstehe es nicht wieso das gelten muss und wieso der teil dann einfach weg fallen kann...?
und was das zu bedeuten hat : Alter Term < Neuer Term (der Rest)
...?
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 16. Okt 2010 20:47 Titel: |
|
|
| Ricky hat Folgendes geschrieben: | Ist der Ind.-Anfang so richtig...
Und könntest du mir bitte den zweiten teil mit <0 nochmal erklären...ich verstehe es nicht wieso das gelten muss und wieso der teil dann einfach weg fallen kann...?
und was das zu bedeuten hat : Alter Term < Neuer Term (der Rest)
...? |
Nein, der ist nicht richtig. Und nein, ich werde dir das nicht nochmal erklären. Wie wäre es, wenn du selber anfängst zu denken und zu rechnen. Und bitte gewöhne dir ab "ich verstehen nicht" zu schreiben: Du willst es nämlich nicht verstehen. Natürlich verstehst du es nicht, wenn du es einfach nur durchliest und dir selber keine Gedanken machst.
Schönen Abend noch.
P.S.: Es steht hier eigentlich schon viel mehr, also du verdient hättest.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 16. Okt 2010 22:25 Titel: |
|
|
also ich muss ehrlich sagen, dass ich es nicht schön finde, was du mir
da schreibst. ich stelle mich nicht dumm, weil ich einfach nur eine lösung
von dir will. du hättest mir die lösung gar nicht schreiben brauchen. ich
hätte sie schritt für schritt auch gern zusammen erarbeitet. ich habe
wirklich verständnisprobleme und bin für jede hilfe dankbar.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 16. Okt 2010 23:13 Titel: |
|
|
jetzt verstehe ich glaube ich was du meinst.
aber wenn ich zeige, dass der ausdruck <0 ist, dann wird der gesamte
ausdruck wie du schon sagtest kleiner. aber dann kann ich die
gesamte gleichung doch nicht mehr beweisen. denn wenn der ausdruck
kleiner wird, dann kann es doch sein, dass die linke seite in der gleichung
also ²}) dadurch größer ist
als ?
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 17. Okt 2010 10:22 Titel: |
|
|
Der alte Ausdruck ( der echt größer als die linke Seite ist) inklusive den zu untersuchenden Term ist kleiner, d.h. wenn du den negativen Term weg lässt, dann vergrößerst du den Ausdruck, es besteht also keinerlei Gefahr, dass die rechte Seite irgendwie kleiner wird. Im Gegenteil du vergrößerst sie ja nur.
Zum Induktionsanfang:
Was ist denn nun
Zum Term: Bring doch diesen Ausdruck mal auf einen Hauptnenner:
²}+\frac{1}{n+1}=...)
Kannst du damit eine Aussage treffen, ob er kleiner als 0, also negativ ist ?
| Zitat: | | ich hätte sie schritt für schritt auch gern zusammen erarbeitet. ich habe wirklich verständnisprobleme und bin für jede hilfe dankbar. |
Wenn das der Wahrheit entspricht, dann musst du besser mitarbeiten. Fünf Minuten nach einem Beitrag von mir einfach zu schreiben "das versteh ich nicht" zählt da nicht. Geh Schritt für Schritt alles durch und versuch dich an den "kleinen Aufgaben", die ich dir gebe, um selber weiter zu kommen. Geb dir Mühe es nachvollziehen und nicht einfach auf, wenn du kurz mal stockst.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 17. Okt 2010 11:00 Titel: |
|
|
Ok. Erst nochmal zum Induktionsanfang :
Ist es nun so richtig....?
Und dann nochmal zu dem anderen Term. Es spielt doch eigentlich keine
Rolle ob der Term nun <0 oder >0 ist. Denn wenn der Termin <0 ist und
man lässt ihn dann einfach weg , dann vergrößert sich ja der Restterm.
Ist der Term jedoch >0, dann vergrößert er doch auch den Restterm....
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 17. Okt 2010 11:09 Titel: |
|
|
Ja, jetzt ist der Induktionsanfang richtig ! 
| Zitat: | Und dann nochmal zu dem anderen Term. Es spielt doch eigentlich keine Rolle ob der Term nun <0 oder >0 ist. Denn wenn der Termin <0 ist und man lässt ihn dann einfach weg , dann vergrößert sich ja der Restterm.
Ist der Term jedoch >0, dann vergrößert er doch auch den Restterm.... |
Doch, es spielt die entscheidende Rolle. Richtig ist, dass wenn er < 0 ist und man ihn weg lässt, dann vergrößert sich der Ausdruck. Wenn er nun > 0 ist den vergrößert er den Rest, aber genau deswegen verkleinert er ja den Ausdruck, wenn man ihn weg lässt. Und ist das der Fall, hast du das Problem, dass er ggf. kleiner als die linke Seite geworden ist und du somit die Behauptung nicht zeigen kannst.
|
|
|
Ricky
Anmeldungsdatum: 16.01.2009
Beiträge: 1000
|
| Ricky Verfasst am: 17. Okt 2010 11:15 Titel: |
|
|
Also muss ich den Induktionsanfang immer so ausführlich mit dem
aufsummieren aufschreiben...? Denn bei meiner ersten Induktionsaufgabe
in dem Topic hier hat es ja auch gereicht einfach die Zahlen einzusetzten...?
Und das mit dem anderen Term habe ich nicht bedacht. Stimmt, wenn er
>0 ist und man lässt ihn weg dann verkleinert er ja den Rest. Ok...dann
versuche ich das mal auf einen Nenner zu bingen und zu zeigen das gilt:
<0 ... wenn ich es glaube geschafft zu haben melde ich mich dann wieder ; )
|
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 17. Okt 2010 11:25 Titel: |
|
|
| Ricky hat Folgendes geschrieben: | Also muss ich den Induktionsanfang immer so ausführlich mit dem
aufsummieren aufschreiben...? Denn bei meiner ersten Induktionsaufgabe
in dem Topic hier hat es ja auch gereicht einfach die Zahlen einzusetzten...? |
Wenn eine Summenzeichen da steht, dann muss man nun mal aufsummieren. Bei der ersten Aufgabe hattest du nur das Glück, dass die Summen, weil du mit n=1 anfangen konntest (was diesmal nicht der Fall ist), nur einen Summanden hatte, du das Summenzeichen also weglassen konntest.
|
|
|
|
Registrieren
Login
FAQ
Suchen
