| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 25. Mai 2023 09:29 Titel: FAQ - Dekohärenz TomS Verfasst am: 25. Mai 2023 09:29 Titel: FAQ - Dekohärenz |
 |
|
Im Folgenden werde ich ein paar Ergebnisse der Dekohärenz zusammenfassen (und später in den Kontext verschiedener Interpretationen der Quantenmechanik stellen).
Axiome
Zu Beginn die zentralen Axiome, die im Folgenden verwendet werden:
1) Die Beschreibung eines Quantensystems] erfolgt im Rahmen eines separablen Hilbertraumes 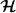 . .
2) Der Zustand eines einzelnen Quantensystems wird vollständig durch einen normierten Vektor 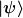 als Element dieses Hilbertraumes als Element dieses Hilbertraumes 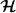 beschrieben. beschrieben.
3) Die Zeitentwicklung eines einzelnen isolierten Quantensystems wird durch einen unitären Zeitentwicklungsoperator
 = e^{ -\mathrm{i}Ht })
mittels
\rangle = U(t)\,|\psi(0)\rangle)
beschrieben; 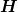 ist dabei der Hamiltonoperator. ist dabei der Hamiltonoperator.
(3) Diese Regel ist vollständig äquivalent zur Schrödingergleichung.
Ein Quantensystem ist dabei nicht irgendwie mikroskopisch. Es umfasst i.A. ein Subsystem, das gemessen wird (Atom, Molekül ... Universum), das Messgerät, die Umgebung (Luft, Staub, Strahlung ...) und ggf. den Beobachter.
Auf Ebene der Axiome erfolgt keine Auszeichnung oder Aufteulung dieser Subsysteme, insbs. keine Auszeichnung des Beobachters. Es erfolgt keine irgendwie geartete Auszeichnung des Messprozesses; dieser ist für spezielle Systeme bzw. deren Hamiltonoperatoren in (3) enthalten!
Für die Mathematik der Dekohärenz benötigen wir keine weiteren Postulate! Wir werden später zur Interpretation des Formalismus die Bornsche Regel heranziehen. Auch die Diskussion des Kollapspostulates erfolgt später.
Beispiel
Zunächst ein sehr einfaches, klassisches Beispiel gemäß
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.26.1862
Environment-induced superselection rules
W. H. Zurek
Phys. Rev. D 26, 1862 – Published 15 October 1982; Received 9 February 1982
ABSTRACT
We show how the correlations of a quantum system with other quantum systems may cause one of its observables to behave in a classical manner. In particular, "reduction of the wave packet," postulated by von Neumann to explain definiteness of an outcome of an individual observation, can be explained when a realistic model of an apparatus is adopted. Instead of an isolated quantum apparatus with a number of states equal to the number of possible distinct outcomes of the measurement, discussed by von Neumann, we consider an apparatus interacting with other physical systems, described here summarily as "environment." The interaction of the quantum apparatus with the environment results in correlations. Correlations impose effective superselection rules which prevent apparatus from appearing in a superposition of states corresponding to different eigenvalues of the privileged pointer observable. It is the propagation of the correlations with the pointer basis states which is ultimately responsible for the choice of the pointer observable. It can be thought of as a process of amplification in which the state of many distinct physical systems becomes correlated with the pointer basis state. Whether these environment systems are regarded as a part of the apparatus setup, or as a part of its environment is irrelevant. What is crucial is the redundancy of the record concerning the pointer observable which is imprinted into the correlations. Eigenspaces of the pointer observable provide a natural basis for the pointer of the quantum apparatus and determine the to-be-measured observable of the quantum system. Decay of those elements of the apparatus-system density matrix, which are off-diagonal in the pointer observable, is caused by the natural evolution of the combined system-apparatus-environment object. For a hypothetical finite environment with N distinct eigenvalues of the apparatus-environment interaction Hamiltonian, off-diagonal terms will decay to become of the order of 1/N^½, and will recur only on a Poincaré time scale. No recurrences will be observed in realistic circumstances. As the correlations spread through the environment on a time scale typically much shorter than the recurrence time scale calculated for the environment already correlated with the pointer observable, the measurement becomes effectively irreversible. Relevance of this model of the measurement process for the understanding of the second law of thermodynamics and its relation to Bohr's "irreversible act of amplification" is briefly discussed. The emergence of the pointer observable can be interpreted as a clue about the resolution of the measurement problem in case of no environment. It points towards the possibility that properties of quantum systems have no absolute meaning. Rather, they must be always characterized with respect to other physical systems.
Zurek betrachtet ein System S, bestehend aus einen Subsystem A - einem einzelnen QBit - sowie einem Environment E - N weiteren QBits. Die QBits werden mittels Spins beschrieben, wir schreiben jedoch 0, 1 statt "up", "down" oder +½, -½. Die Spins sind "eingefroren" bzgl. der freien Dynamik, d.h. der Hamiltonian hat keinen kinetischen Term; wir beschränken uns auf die Wechselwirkung

Jeder Summand des k-ten Spins in der Umgebung steht für

wobei wir die Eins-Operatoren in der verkürzten Notation weglassen.
Dieser Operator liefert in gewisser Weise ein Modell für Messung der z-Komponenten des Systems A sowie eine Verschränkung mit der Umgebung. Die Zeitentwicklung resultiert in einer mathematischen Struktur, aus der man die Messergebnisse ablesen kann. Es gibt jedoch keine separaten Zeigervariablen, die das Ergebnis der Messung tatsächlich anzeigt; der Spin selbst ist der Zeiger. (Diese Variablen könnten zusätzlich modelliert werden, sind jedoch für den Effekt der Dekohärenz und die spätere Interpretation bzgl. Messung und Beobachtung unwesentlich).
Das System ist initial in einem Zustand

mit

)

präpariert.
Die Zeitentwicklung führt auf
\rangle = e^{-iHt}\,|\psi\rangle = a|0\rangle \otimes |E_0(t)\rangle + b|1\rangle \otimes |E_1(t)\rangle \qquad (D))
mit
\rangle = |E_1(-t)\rangle = \bigotimes_{k=1}^N \left( a_k e^{ig_kt}|0\rangle + b_k e^{-ig_kt}|1\rangle \right) )
Dies ist die vollständige mathematische Struktur des Gesamtzustandes nach Messung mit Messdauer t. Dieser Zustand entspricht offenbar nicht der einfachen Struktur nach von Neumann. Allerdings kann man diese mittels geeigneter mathematischer Methoden "herauspräparieren". Dazu verwirft man sämtliche in einem realen Experiment unbeobachtbare Umgebungsvariablen, d.h. man berechnet die reduzierte Dichtematrix für A durch Ausspuren der Umgebung E
 = |\psi(t)\rangle\langle\psi(t)|)
 = \text{tr}_E \, \rho(t) = |a|^2 \, |0\rangle\langle 0| + |b|^2 \, |1\rangle\langle 1| + ab^\ast r(t) |0\rangle\langle 1| + a^\ast b r^\ast(t) |1\rangle\langle 0| )
Der Koeffizient
 = \langle E_0(t)| E_1(t)\rangle)
verschwindet extrem schnell für genügend viele Umgebungsfreiheitsgrade, d.h. genügend großes N. Die Umgebung erzwingt sozusagen die Orthogonalität verschiedener Komponenten. Damit bleibt
 \simeq |a|^2 \, |0\rangle\langle 0| + |b|^2 \, |1\rangle\langle 1| )
was aussieht wie ein klassisches statistisches Ensemble zweier Zustände.
Man muss jedoch beachten, dass das Ausspuren keinem physikalischen Prozess entspricht, d.h. die Interferenzterme verschwinden nicht, ihre Effekte werden nur unsichtbar. Man findet
 = \prod_{k=1}^N r_k(t))
mit
|^2 = 1 - \left(|a_k|^2 - |b_k|^2 \right))
d.h. die Koeffizienten, die die Verschränkung des gemessenen Spins mit einem einzelnen Spin der Umgebung beschreiben, können von der Größenordnung Eins sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 25. Mai 2023 22:58, insgesamt 3-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 25. Mai 2023 16:29 Titel: TomS Verfasst am: 25. Mai 2023 16:29 Titel: |
 |
|
Um die Irrtümer gar nicht erst entsehen zu lassen ...
1) Das Ergebnis der Dynamik des Systems ist
\rangle = e^{-iHt}\,|\psi\rangle = a|0\rangle \otimes |E_0(t)\rangle + b|1\rangle \otimes |E_1(t)\rangle \qquad (D))
bzw.
 = |\psi(t)\rangle\langle\psi(t)|)
nicht jedoch
 = \text{tr}_E \, \rho(t) )
Diese reduzierte Dichtematrix entspricht einem formalen Werkzeug, das sozusagen eine "grobe Skizze" darstellt, die viele Details auslöscht.
2) Diese "grobe Skizze" führt auf
 \simeq |a|^2 \, |0\rangle\langle 0| + |b|^2 \, |1\rangle\langle 1| )
was lediglich aussieht wie ein klassisches statistisches Ensemble zweier Zustände.
Der volle quantenmechanische Zustand gemäß (D) ist aber kein statistisches Ensemble.
3) Die quantenmechanischen Interferenzen verschwinden nicht. Die Interferenz ist im vollen Zustand enthalten, sie wandert sozusagen in die Verschränkung des gemessenen Spins mit der Umgebung und wird in der "Skizze" durch das Ausspuren der Umgebung unsichtbar. Interferenzterme sind für sehr kleine Subsystems (der gemessene Spin sowie ein Spin aus der Umgebung) nicht klein.
4) Die Dekohärenz bzw. die Dichtematrix liefern keine klassischen Wahrscheinlichkeiten, denen zufolge entweder das eine oder das andere gegeben wäre. Dies erfordert weitere Axiome und zusätzliche Interpretation. Ich hatte in den Axiomen oben explizit keine Wahrscheinlichkeiten eingeführt.
5) Weder erklärt noch ersetzt Dekohärenz den Kollaps der Wellenfunktion. Erstens sind sogar in der "Skizze" alle Komponenten sichtbar, und zweitens ist das Ergebnis der Dekohärenz eben gerade nicht nur diese "Skizze" sondern der volle Zustand (D), in dem alle Komponenten weiterhin enthalten sind. Die immer wieder zu findende Behauptung, Dekohärenz bringe einzelne Komponenten des Zustandes bzw. der Superposition zum Verschwinden, ist offensichtlich falsch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 25. Mai 2023 18:04 Titel: TomS Verfasst am: 25. Mai 2023 18:04 Titel: |
 |
|
Was die Dekohärenz leistet:
1) Die Dekohärenz liefert präzisiere Modelle als den eher skizzenhaften Messprozess nach von Neumann, sowie eine Rechtfertigung des mathematischen Teils von Everett’s Relative State Interpretation
2) Die Dekohärenz selektiert dynamisch die korrekte Basis, bzgl. derer die "Zweigstruktur" gültig ist. Diese Basis ist im o.g. Beispiel festgelegt durch die im Hamiltonoperator ausgezeichnete z-Komponente des gemessenen Spins. Nur bzgl. dieser Größe wird die reduzierte Dichtematrix diagonal. Diese Eigenschaft ist robust, d.h. bleibt unter Zeitentwicklung stabil, und sie ist generisch, d.h. hängt kaum von den Anfangsbedingungen der Umgebung ab. D.h. die Dynamik = der Hamiltonoperator selektiert die Basis, sie muss nicht wie in der orthodoxen Interpretation postuliert werden.
3) Die Dekohärenz liefert damit die "Klassizität", d.h. die Robustheit klassischer Zustände und insbs. die Abwesenheit von Superposition klassisch unterscheidbarer Zustände.
Die Erklärung für die Robustheit der Zweigstruktur sowie die wechselseitige Interferenzfreiheit versteht man wie folgt. Das Gesamtsystem entwickelt sich gemäß des o.g. Hamiltonians in den Zustand
\rangle = e^{-iHt}\,|\psi\rangle = a|0\rangle \otimes |E_0(t)\rangle + b|1\rangle \otimes |E_1(t)\rangle \qquad (D))
Betrachtet man stattdessen zwei isolierte Systeme, die nicht miteinander in Wechselwirkung treten, so wird dies mittels eines Hamiltonians



beschrieben.
Damit folgt
\rangle = e^{-ih_0 t} e^{-ih_1 t} \, |\psi\rangle = a|0\rangle \otimes |\tilde{E}_0(t)\rangle + b|1\rangle \otimes |\tilde{E}_1(t)\rangle )
Der tatsächliche Zeitentwicklungsoperator
 = e^{-iHt})
liefert für die beobachtbaren Subsysteme - hier also den gemessenen Spin sowie ggf. weitere Zeigervariablen - die selbe Dynamik, wie der künstlich konstruierte Zeitentwicklungsoperator voneinander isolierter Systeme
 = e^{-iht} = e^{-ih_0t} \, e^{-ih_1t})
D.h. die Unterschiede zwischen den Zeitentwicklungen stecken in den unbeobachtbaren Umgebungsfreiheitsgraden.
Zurek prägte dafür den Begriff Einselection = "environment-induced superselection".
Die Klassizität der einzelnen Zweige wird als emergente Eigenschaft beschrieben, die in einem offenen Quantensystem (dem beobachteten Subsystem) durch die (unbeobachtbare) Umgebung induziert wird. Nach einer Dekohärenzzeit, die bei makroskopischen Objekten in der Regel um viele Größenordnungen kürzer ist als jede andere dynamische Zeitskala, zerfällt ein allgemeiner Quantenzustand in einen Zustand, der als eine statistische Mischung dynamisch entkoppelter, stabiler Zweige oder Zeigerzustände ausgedrückt werden kann. Die Einselection schließt somit die stabile Existenz der Superposition von klassisch unterscheidbaren Zeigerzuständen aus.
4) Die Dekohärenz erklärt, was eine Messung ist. Die Messung einer Observablen liegt dann vor, wenn aus der Zeitentwicklung mit Dekohärenz eine entsprechende Zweigstruktur der reduzierten Dichtematrix folgt, in der Zeigervariablen eine stabile Korrelation mit der zu messenden Observablen aufweisen (hatten wir im obigen Beispiel nicht explizit eingeführt der Spin selbst fungierte hier als Zeigervariable).
5) Die Dekohärenz erklärt aufeinanderfolgende Messungen ohne Kollaps. Die übliche Erwartungshaltung ist, dass eine auf die erste Messung bis zu t_1 folgende zweite Messung bis zu t_2 der selben Observablen auf die selbe Zeigerposition führt; dies war der Ausgangspunkt für das Projektionspostulat. Unter Einfluss der Dekohärenz ist dies trivialerweise gegeben, da die "Zweigstruktur" unter Zeitentwicklung stabil bleibt (wenn man nicht eine andere Observable misst, also einen anderen Hamiltonoperator einführt).
 \simeq \rho_A(t_2) \simeq |a|^2 \, |0\rangle\langle 0| + |b|^2 \, |1\rangle\langle 1| )
ist in extrem guter Näherung gültig und zeitunabhängig, d.h. stabil. Für die ausgespurten Freiheitsgrade der Umgebung sowie ihre Verschränkungen gilt dies nicht; ihre zeitlichen Fluktuationen zerstören jedoch diese Struktur nicht.
Die Dekohärenz löst also das Messproblem - bis auf zwei weiterhin offene Punkte: Sie erklärt nicht
A) warum eine Messung immer auf nur ein einziges Messergebnis führen, und auf welches.
B) warum wir über alle möglichen Messergebnisse eine Wahrscheinlichkeitsverteilung sehen, und warum diese der Bornschen Regel folgt.
Ausblick
Bis hierher ist die Darstellung verträglich mit diversen Interpretationen der Quantenmechanik. Sie erlaubt natürlich das Einführen von Wahrscheinlichkeiten gemäß der Bornschen Regel. Sie liefert dann eine Zweigstruktur wie bereits bei von Neumann und Everett - jeweils ohne Begründung durch mikroskopische Freiheitsgrade und Dekohärenz - und erlaubt die Berechnung von Wahrscheinlichkeiten für aufeinanderfolgende Messungen.
Mit Projektionspostulat ist das klar. Bei zwei möglichen Messergebnissen K_1, L_1 mit Wahrscheinlichkeiten p(K_1) und p(L_1) in der ersten Messung lautet das Projektionspostulat nach einer Beobachtung von K_1
 \simeq p(K_1) \, \hat{E}_{K_1} + p(L_1) \, \hat{E}_{L_1} \to \left[\frac{1}{p(K_1)} \, \hat{E}_{K_1}\right] \, \rho_A = \hat{E}_{K_1})
Für die zweite Messung wird die folgende Zeitentwicklung auf Basis des kollabierten Zustandes berechnet, und man erhält
 \simeq p(M_2) \, \hat{E}_{M_2} + p(N_2) \, \hat{E}_{N_2} )
für neue mögliche Messergebnisse, woraus man die Wahrscheinlichkeiten für M_2 und N_2 unmittelbar ablesen kann (die zweite Messung kann die selbe oder eine andere Observable messen)
Ohne Projektionspostulat erhält man eine weitere Auffächerung
 \simeq p(K_1) \, \left[ p(M_2) \, \hat{E}_{M_2} + p(N_2) \, \hat{E}_{N_2} \right] + p(L_1) \, \left[ \ldots \right] )
Zur Berechnung der Wahrscheinlichkeit der Messung von z.B. N_2 verwendet man entsprechend der Everettschen Relative State Interpretation bedingte Wahrscheinlichkeiten. D.h. nach Beobachtung von K_1
 = \frac{P(K_1 \cap N_2)}{P(K_1)} = \frac{p(K_1) \cdot p(N_2)}{p(K_1)} = p(N_2))
in Übereinstimmung mit der Berechnung nach von Neumann mit Kollaps.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















