Formel für nachlassende Helligkeit mit der Distanz gesucht.

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Hallo,

ich bin auf der Suche nach einer Formel mit der man die nachlassende Helligkeit eines Lichtkegels über die Distanz & dem Abstrahlwinkel beschreibt.
Es gibt ja LED Dioden die 60°, 90° oder 120° Abstrahlwinkel haben.
Das 1/r^2 Gesetz gilt aber nur für punktförmige Lichtquellen, die 360° abstrahlen. Das ergibt eine Kugel bzw. eine Kugeloberfläche.
Ich nehme bei der Diode auch eine zentrale punktförmige Lichtquelle an, mit idealem Reflektor.
Wenn ich jetzt 90° Abstrahlwinkel habe, strahlt das Licht in einen Kegel aus der 1/6tel des Volumens der Kugel des 360° Strahlers haben müsste, die Oberfläche am Ende des Kegels müsste auch nur 1/6tel betragen.

Ich möchte also die Formel so erweitern, daß man den Abstrahlwinkel auch noch einträgt, um dann z.B. umstellen zu können, um ausrechnen zu können, ab welcher Distanz eine gleiche Beleuchtungsstärke bei unterschiedlichem Abstrahlwinkel vorliegt.

Meine Idee:
Die Strahlungsintensität I
Der Abstrahlwinkel a
I=1/r^2 *(360°/a)
Leider stimmt das nicht Hammer

Bei 180° ist das Ergebnis korrekt, aber bei 90° kommt 4 heraus, obwohl es 6 sein müsste. Der Abstrahlwinkel ist 2-dimensional, aber der Lichtkegel dreidimensional. Wie kann man das umrechnen?

Frankx · Anmeldungsdatum: 04.03.2015 Beiträge: 982

Entscheidend ist die Fläche, auf welche das Licht fällt. An Stelle der Kugeloberfläche mit Abstand r muss man nun die Kreisfläche des Bodens des Kegels der Höhe r ansetzen.

.

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Nur wie berechne ich das? Es ist streng genommen ja keine Kreisfläche, da die Fläche leicht gewölbt ist. Was wiederum zu leicht mehr Fläche führt.
Deswegen wollte ich mit einem Bruchteils des Volumen der Kugel rechnen. Ist es nicht möglich, von dem Abstrahlwinkel ein Verhältniss zu bilden?

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Volumen Kugelausschnitt:
V=(2*Pi/3)*r^3*(1-cos(Winkel))

Quelle:
https://de.wikipedia.org/wiki/Kugelausschnitt?wprov=sfla1

Leider wird dort in der Zeichnung der Winkel nicht dargestellt, obwohl darauf verwiesen wird. Kann ich davon ausgehen, daß die der Winkel ist der von dem Zentrum ausgeht und die Kwgelspitze bildet? Weil das wäre nämlich auch der Abstrahlwinkel.

r wäre dann der Messpunkt wo man den Sensor des Luxmeters positioniert.

Das Volumen der Kugel geteilt durch das Volumen des Kugelauschnittes ergäbe dann ein Co-Faktor C um die Intensität proportional zu erhöhen:
I=(1/r^2)*C

Ist der Denkansatz so richtig?

Weil, ich habe die Fläche nicht. Ich habe Abstrahlwinkel & Messdistanz.

Frankx · Anmeldungsdatum: 04.03.2015 Beiträge: 982

Bei kleinem Winkel könnte man die Wölbung vernachlässigen und mit einer Kreisfläche rechnen.
Ansonsten müsste man den entsprechenden Teil der Kugeloberfläche betrachten.

Das Volumen des Kugelausschnittes spielt dagegen keine Rolle.

.

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Volumen Kugel:
V = 4/3 * Pi * r^3

Volumen Kugelausschnitt:
V = (2*Pi/3) * r^3 * (1-cos(Winkel))

Abstandsquadratgesetz: (360° Punktstrahler)
I = 1/r^2

Zusammen:
I = 1/r^2 * [(4/3 * Pi * r^3) / (2*Pi/3) * r^3 * (1-cos(Winkel))]

Ist das so überhaupt richtig ausgeschrieben?

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5852

Siehe hier.

Bei einem Öffnungswinkel

müsste die Intensität um den Faktor

erhöht sein gegenüber einer Diode, die isotrop in alle Richtungen, also den vollen Raumwinkel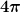

, abstrahlt. Bei 90° ergäbe das allerdings etwa 6.8, nicht 6.

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Danke, ist das die Formel?

Bei mir kommt ~2.6 heraus unglücklich

Wie geb ich denn Sinus^2 in den Taschenrechner ein?

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Ah nach der Klammer.
Ergebniß:
6,8284271247461

Kassiopeija · Anmeldungsdatum: 26.06.2015 Beiträge: 146

Bei 120° Abstrahlwinkel kommt dann 4 heraus. Wie wird denn diese Zahl richtigerweise benannt?

Die Formel wäre dann:
1÷(sin(Öffnungswinkel÷4)^2)

140°=~3.04
120°=4
90=~6.83
60°=14.93

und zur Kontrolle
180°=2
360°=1

Ja, das passt! Vielen Dank!! Die Formel ist sogar simpler smile