| Autor |
Nachricht |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 11:18 Titel: Doppelpendel Formel Marina17 Verfasst am: 22. Aug 2016 11:18 Titel: Doppelpendel Formel |
 |
|
Meine Frage:
Hallo,
für meine W-Seminararbeit in der Schule muss ich eine Simulation von einen Doppelpendel Programmieren jedoch komme ich leider bei der Formel nicht weiter. Ich hänge zurzeit bei der Formel für die kinetische Energie. Bei dieser Formel werden Punkte über die Formelzeichen gesetzt. Was bedeuten diese? und wie kann ich mit ihnen rechnen? Ist auf dieser Seite: http://scienceworld.wolfram.com/physics/DoublePendulum.html der Übergang von Schritt 7 zu 8. Wär nett wenn du mir weiterhelfen kannst.
Viele Grüße
Meine Ideen:
Ich glaube bin mir aber nicht sicher, dass die Punkte über den Formelzeichen die Ableitung bedeuten sollen aber ich hab auch keine Ahnung wie ich die dann ableiten kann. |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 22. Aug 2016 12:19 Titel: hansguckindieluft Verfasst am: 22. Aug 2016 12:19 Titel: |
 |
|
Hallo,
mit einem Punkt über einer Größe kennzeichnet man in der Physik eine Ableitung nach der Zeit.

Theta ist ja der Winkel.  ist daher die Winkelgeschwindigkeit. ist daher die Winkelgeschwindigkeit.
Gruß |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 13:09 Titel: Marina17 Verfasst am: 22. Aug 2016 13:09 Titel: |
 |
|
Hallo,
Danke für die Antwort. Soll das d davor ein delta sei? und muss ich es mit berücksichtigen? |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 13:19 Titel: Marina17 Verfasst am: 22. Aug 2016 13:19 Titel: |
 |
|
Hallo,
noch eine Frage. Warum wird aus der Geschwindigkeit im quadrat die Länge l1 ins quadrat mal die Ableitung vom Winkel theta ins quadrat?[/latex] |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 22. Aug 2016 13:28 Titel: hansguckindieluft Verfasst am: 22. Aug 2016 13:28 Titel: |
 |
|
Hallo,
mal der Reihe nach:
die Schreibweise:  meint einfach: meint einfach:
Ableitung von Theta nach der Zeit. Ich weiß nicht, wie Ihr üblicherweise Ableitungen hinschreibt. Aber wenn der Winkel Theta eine Funktion der Zeit t ist, dann kann man ja schreiben:
)
Dann ist die Ableitung von Theta  = \frac{d\theta }{dt} )
Das "d" kennzeichnet ein "Differenzial".
Zu Deiner zweiten Frage:
Die Bahngeschwindigkeit der Masse 1 (also die tangentiale Geschwindigkeit) ist ja gleich der Winkelgeschwindigkeit multipliziert mit dem Radius.
Also:
Kannst Du das nachvollziehen?
Gruß |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 13:50 Titel: Marina17 Verfasst am: 22. Aug 2016 13:50 Titel: |
 |
|
Hallo,
Danke das mit der Geschwindigkeit habe ich jetzt kapiert. Jedoch hänge ich jetzt an der nächsten Stelle immer noch bei Schritt 8. Als erstes wird die kinetische Energie von der ersten Kugel ausgerechnet und dann von der zweiten jedoch wird bei der zweiten Kugel bei der Geschwindigkeit erst die Geschwindigkeit von der ersten Kugel dann von der zweiten Kugel und dann von noch was anderen addiert. Was für eine Geschwindigkeit ist es die noch dazu addiert wird. Und noch mal zum sichergehen bei der Ableitung des Winkels ist ja immer ein d davor. Bei der Berechnung darf ich dann das d einfach weglassen und ohne den d rechnen? |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 22. Aug 2016 14:37 Titel: Steffen Bühler Verfasst am: 22. Aug 2016 14:37 Titel: |
 |
|
Ich spring mal kurz ein.
| Marina17 hat Folgendes geschrieben: | | Was für eine Geschwindigkeit ist es die noch dazu addiert wird. |
Du addierst ja hier zwei Vektoren (Betrag und Richtung der Geschwindigkeit), die nicht unbedingt senkrecht aufeinanderstehen, zu einem dritten. Dieser dritte Term kommt im nichtsenkrechten Fall noch dazu.
| Marina17 hat Folgendes geschrieben: | | Bei der Berechnung darf ich dann das d einfach weglassen und ohne den d rechnen? |
Nein. Wenn Du eine Stunde läufst und dabei fünf Kilometer zurücklegst, ist Deine Durchschnittsgeschwindigkeit zwar in der Tat 5km/h gewesen. Hier geht es aber um die Momentangeschwindigkeit. Du könntest ja mal kurz auch bei 8km/h gewesen sein. Und die kann man eben nur ausrechnen, indem man einen sehr kleinen (eben differentiellen, daher das d) Wegabschnitt durch einen ebenso kleinen Zeitabschnitt dividiert. |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 15:03 Titel: Marina17 Verfasst am: 22. Aug 2016 15:03 Titel: |
 |
|
Hallo,
Danke fürs einspringen. Aber ich habe das noch nicht so ganz verstanden. Warum brauche ich wenn die zwei Vektoren nicht senkrecht aufeinanderstehen noch eine dritte Größe die ich dazuaddiere? Und was genau macht die dritte Größe? Und das mit dem d heißt ich darf es weglassen wenn ich mit der Methode der kleinen Schritte arbeite? |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 22. Aug 2016 15:28 Titel: Steffen Bühler Verfasst am: 22. Aug 2016 15:28 Titel: |
 |
|
| Marina17 hat Folgendes geschrieben: | | Warum brauche ich wenn die zwei Vektoren nicht senkrecht aufeinanderstehen noch eine dritte Größe die ich dazuaddiere? |
Das ist nun mal der Kosinussatz. Wie addierst Du denn normalerweise einen Vektor der Länge 1 und einen der Länge 2, die den Winkel 40° zueinander haben?
| Marina17 hat Folgendes geschrieben: | | Und das mit dem d heißt ich darf es weglassen wenn ich mit der Methode der kleinen Schritte arbeite? |
Ja. In Deiner Simulation wirst Du ja wahrscheinlich die Zeit in sehr kleinen Intervallen hochzählen, der Quotient Wegänderung:Zeitänderung kann dann in der Tat mit dem Differential gleichgesetzt werden, ohne dass Du einen großen Fehler machst. |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 15:54 Titel: Marina17 Verfasst am: 22. Aug 2016 15:54 Titel: |
 |
|
Hallo,
Mit den Kosinussatz müsste man doch die ersten beiden addieren und dann das letzte sustrahieren? In dieser Formel werden alle drei adddiert. |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 22. Aug 2016 16:08 Titel: Steffen Bühler Verfasst am: 22. Aug 2016 16:08 Titel: |
 |
|
|
Du hast recht, das war wohl zu voreilig von mir. Die Antwort muss ich Dir dann leider schuldig bleiben, tut mir leid. |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 22. Aug 2016 16:21 Titel: hansguckindieluft Verfasst am: 22. Aug 2016 16:21 Titel: |
 |
|
Hallo,
ich denke, das liegt hier daran, dass man den Winkel mit ) definiert hat. definiert hat.
Wenn  kleiner als kleiner als  ist, kommt das Minus- Zeichen automatisch aus dem Cosinus. ist, kommt das Minus- Zeichen automatisch aus dem Cosinus.
Man hätte m. E. auch ) schreiben, und vor dem letzten Term ein "-" setzen können. schreiben, und vor dem letzten Term ein "-" setzen können.
Liege ich damit richtig?
Gruß
EDIT: Muss ich nochmal drüber nachdenken. Der Cosinus eines negativen Winkels ist ja nicht unbedingt auch negativ. |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
 Steffen Bühler Verfasst am: 22. Aug 2016 16:23 Titel: Steffen Bühler Verfasst am: 22. Aug 2016 16:23 Titel: |
 |
|
Leider nicht, fürchte ich. Der Cosinus ist gerade:  = \cos (-x)) |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Aug 2016 16:24 Titel: Huggy Verfasst am: 22. Aug 2016 16:24 Titel: |
 |
|
Wenn ich mich mal kurz einmischen darf:
Die geometrischen Beziehungen zwischen den kartesischen Koordinaten (x,y) der Massenpunkte und den Winkeln 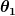 und und  sind in deinem Wolfram-Link in den Gleichungen (1) bis (4) zusammengestellt. Sie ergeben sich aus der Skizze darüber. Die kartesischen Koordinaten der Masse 2 werden zunächst relativ zur Masse 1 bestimmt. Für ihre absoluten Koordinaten müssen dann die Koordinaten der Masse 1 addiert werden. sind in deinem Wolfram-Link in den Gleichungen (1) bis (4) zusammengestellt. Sie ergeben sich aus der Skizze darüber. Die kartesischen Koordinaten der Masse 2 werden zunächst relativ zur Masse 1 bestimmt. Für ihre absoluten Koordinaten müssen dann die Koordinaten der Masse 1 addiert werden.
Der Übergang von (7) zu (8 ist danach lediglich eine Anwendung der Kettenregel. |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 16:31 Titel: Marina17 Verfasst am: 22. Aug 2016 16:31 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | Wenn ich mich mal kurz einmischen darf:
Die geometrischen Beziehungen zwischen den kartesischen Koordinaten (x,y) der Massenpunkte und den Winkeln 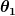 und und  sind in deinem Wolfram-Link in den Gleichungen (1) bis (4) zusammengestellt. Sie ergeben sich aus der Skizze darüber. Die kartesischen Koordinaten der Masse 2 werden zunächst relativ zur Masse 1 bestimmt. Für ihre absoluten Koordinaten müssen dann die Koordinaten der Masse 1 addiert werden. sind in deinem Wolfram-Link in den Gleichungen (1) bis (4) zusammengestellt. Sie ergeben sich aus der Skizze darüber. Die kartesischen Koordinaten der Masse 2 werden zunächst relativ zur Masse 1 bestimmt. Für ihre absoluten Koordinaten müssen dann die Koordinaten der Masse 1 addiert werden.
Der Übergang von (7) zu (8 ist danach lediglich eine Anwendung der Kettenregel. |
Das habe ich jetzt noch nicht so ganz verstanden |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Aug 2016 16:32 Titel: Huggy Verfasst am: 22. Aug 2016 16:32 Titel: |
 |
|
|
Was davon hast du nicht verstanden? |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 16:37 Titel: Marina17 Verfasst am: 22. Aug 2016 16:37 Titel: |
 |
|
|
Den Teil, dass die Koordinaten der Masse m1 zu den Koordinaten der Masse m2 addiert werden müssen um die absoluten Koordinaten der Masse m2 zu erhalten. und das, dass der Übergang von Schritt 7 zu 8 nur die Anwendung der Kettenregel ist. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Aug 2016 16:41 Titel: Huggy Verfasst am: 22. Aug 2016 16:41 Titel: |
 |
|
|
Beginnen wir mal mit den Koordinaten. Hast du verstanden, wie sich die Koordinaten der Masse 1 berechnen? Das sind die Gleichungen (1) und (2). |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 22. Aug 2016 16:41 Titel: hansguckindieluft Verfasst am: 22. Aug 2016 16:41 Titel: |
 |
|
es gilt ja:

beim Zusammenfassen muss folgendes berücksichtigt werden:
+sin^{2}(x)=1)
sowie das Additionstheorem:
\cdot cos(y)+sin(x)\cdot sin(y)=cos(x-y))
Gruß
EDIT: Danke Huggy. Das war der entscheidende Hinweis. Damit komme ich auch auf das Ergebnis. Halte mich jetzt erstmal zurück. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Aug 2016 16:45 Titel: Huggy Verfasst am: 22. Aug 2016 16:45 Titel: |
 |
|
@ hansguckindieluft
Das Additionstheorem wird überhaupt nicht benötigt. |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 22. Aug 2016 16:47 Titel: hansguckindieluft Verfasst am: 22. Aug 2016 16:47 Titel: |
 |
|
ok. Ich habe es benutzt. Vielleicht geht es auch ohne.
Wie gesagt, halte ich mich jetzt erstmal zurück, um nicht noch mehr Verwirrung zu stiften. |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 22. Aug 2016 17:00 Titel: Marina17 Verfasst am: 22. Aug 2016 17:00 Titel: |
 |
|
| hansguckindieluft hat Folgendes geschrieben: |

|
Wenn ich das jetzt hernehme hab ich aber wenn ich einsetze das Problem, dass ich noch den Punkt drüber hab also eigentlich nach der Zeit ableiten muss und nicht zusammenfassen kann. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 22. Aug 2016 17:17 Titel: Huggy Verfasst am: 22. Aug 2016 17:17 Titel: |
 |
|
Dazu sagte ich doch: Kettenregel
Nehmen wir mal die Masse 1. Dann gilt

Nun gilt nach (1):

Nach Kettenregel gilt:
 \dot \theta_1)
Analog für . Anschließend vereinfacht sich das Ganze wegen: . Anschließend vereinfacht sich das Ganze wegen:
 |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 23. Aug 2016 09:55 Titel: Marina17 Verfasst am: 23. Aug 2016 09:55 Titel: |
 |
|
Hallo,
irgendwie kommt bei mir nicht das richtige raus obwohl ich die Kettenregel benutze. Ich kann eigentlich alles am Ende bei mir wegkürzen |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 23. Aug 2016 10:06 Titel: Marina17 Verfasst am: 23. Aug 2016 10:06 Titel: |
 |
|
|
Wie kann ich vereinfachen wenn ich in einer Klammer zwei Produkte addiere und die Klammer hoch zwei ist? |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 23. Aug 2016 10:26 Titel: hansguckindieluft Verfasst am: 23. Aug 2016 10:26 Titel: |
 |
|
| Marina17 hat Folgendes geschrieben: | | Wie kann ich vereinfachen wenn ich in einer Klammer zwei Produkte addiere und die Klammer hoch zwei ist? |
erstmal die Klammer ausmultiplizieren (oder binomische Formel anwenden).
Dann sortieren und zusammenfassen.
Gruß |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 23. Aug 2016 10:32 Titel: Marina17 Verfasst am: 23. Aug 2016 10:32 Titel: |
 |
|
|
Jetzt hab ich ich habe aber auch das Additionstheorem gebraucht. Vielen Dank für eure Hilfe |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 27. Aug 2016 11:50 Titel: Marina17 Verfasst am: 27. Aug 2016 11:50 Titel: |
 |
|
Hallo nocheinmal,
heute hatte ich jetzt eigentlich vor an der Formel weiterzuarbeiten aber ich kann nichts mit der Langrange Funktion anfangen. Kann die mir jemand erklären? |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 27. Aug 2016 12:55 Titel: hansguckindieluft Verfasst am: 27. Aug 2016 12:55 Titel: |
 |
|
Hallo,
das Prinzip, welches dahinter steckt, nennt sich "Prinzip der kleinsten Wirkung", oder auf englisch "principle of least action".
Vereinfach könnte man sagen: Ein Körper, der sich selbst überlassen wird (z. B. ein Ball, den Du wirfst) verhält sich immer so, dass eine bestimmte Größe minimal (eigentlich stationär) wird. Diese Größe ist die "Wirkung". Die Wirkung ist das Integral der Lagrangefunktion L=T-V, über die Zeit, wobei T die kinetische Energie und V die potenzielle Energie ist. Von allen denkbaren Flugbahnen wird der geworfene Ball also die Flugbahn ausführen, bei der die Wirkung minimal ist. Das Prinzip lässt sich auch auf das Doppelpendel anwenden.
zum Einstieg könntest Du z. B. hier nachsehen:
http://www.feynmanlectures.caltech.edu/II_19.html
https://m.youtube.com/watch?v=3apIZCpmdls
In der Vorlesungsreihe von Prof. Susskind wird auch das Doppelpendel besprochen (wenn auch nicht komplett durchgerechnet).
Gruß |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 27. Aug 2016 21:24 Titel: Re: Doppelpendel Formel franz Verfasst am: 27. Aug 2016 21:24 Titel: Re: Doppelpendel Formel |
 |
|
Nur eine Frage am Rande
| Marina17 hat Folgendes geschrieben: | | Simulation von einen Doppelpendel Programmieren |
Was hat die Simulation (verstehe ich als hübsche Darstellung der Schwingung nach Einstellung von Startwerten) mit der Herleitung / Lösung der entsprechenden Bewegungsgleichung zu tun? Warum sich nicht auf die Programmierung / Ein- und Ausgabe beschränken - bei Verwertung eines fertigen Ergebnisses? |
|
 |
yukterez

Anmeldungsdatum: 20.09.2014
Beiträge: 96
|
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 06. Sep 2016 14:31 Titel: Marina17 Verfasst am: 06. Sep 2016 14:31 Titel: |
 |
|
Hallo,
ich habe ein Beispiel zur verwendung der Langrange Funktion gefunden http://theory.gsi.de/~vanhees/faq/lagrange/node13.html bei diesem Beispiel wird für den ersten Teil der Formel einfach V abgeleitet und für den zweiten Teil der Formel T. Stimmt das so? Oder kann mir jemand erklären wie ich ihn sonst anwenden kann ich hab das noch nicht so ganz verstanden? |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 06. Sep 2016 19:12 Titel: hansguckindieluft Verfasst am: 06. Sep 2016 19:12 Titel: |
 |
|
Hallo,
| Marina17 hat Folgendes geschrieben: | | bei diesem Beispiel wird für den ersten Teil der Formel einfach V abgeleitet und für den zweiten Teil der Formel T. Stimmt das so? |
Die Euler- Lagrange- Gleichung lautet ja für das Beispiel:

Das heißt, die Lagrangefunktion wird zunächst partiell nach  abgeleitet, und das Ergebnis daraus nochmal nach der Zeit t. Dann wird im zweiten Term die Lagrangefunktion partiell nach abgeleitet, und das Ergebnis daraus nochmal nach der Zeit t. Dann wird im zweiten Term die Lagrangefunktion partiell nach  abgeleitet. Es wird also jeweils die gesamte Lagrangefunktion abgeleitet. In dem Beispiel hängt die kinetische Energie aber nicht von der Koordinate abgeleitet. Es wird also jeweils die gesamte Lagrangefunktion abgeleitet. In dem Beispiel hängt die kinetische Energie aber nicht von der Koordinate  ab, sondern nur von der Geschwindigkeit ab, sondern nur von der Geschwindigkeit 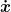 . Die potenzielle Energie dagegen hängt hier nur von der Koordinate . Die potenzielle Energie dagegen hängt hier nur von der Koordinate  ab und nicht von ab und nicht von 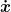 . Von der Zeit t hängt wiederum nur die kinetische Energie ab. . Von der Zeit t hängt wiederum nur die kinetische Energie ab.
Gruß |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 09. Sep 2016 16:32 Titel: Marina17 Verfasst am: 09. Sep 2016 16:32 Titel: |
 |
|
Hallo,
Danke für die Hilfe! Jetzt habe ich zwar verstanden wie es in die Gleichung eingesetzt wurde aber ich weiß jetzt nicht, wie ich die Formel nach den Winkeln auflösen kann. Kann mir da jemand weiterhelfen? |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 09. Sep 2016 18:32 Titel: hansguckindieluft Verfasst am: 09. Sep 2016 18:32 Titel: |
 |
|
Hallo,
Du meinst, wie Du die Differentialgleichungen lösen kannst?
Das wird eben nur numerisch funktionieren. Schau Dir mal die komplizierten Winkelverläufe in dem von Dir eingangs geposteten Link an. Die lassen sich kaum durch eine Funktion beschreiben.
Zur numerischen Lösung von DGLs gibt es verschiedene Verfahren. Schau z. B. mal nach dem "expliziten Euler- Verfahren" oder "Runge- Kutta". Oder generell nach numerischen Lösungsverfahren für Differentialgleichungen.
Es gibt natürlich auch fertige Software, die soetwas kann.
Gruß |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 10. Sep 2016 11:56 Titel: Marina17 Verfasst am: 10. Sep 2016 11:56 Titel: |
 |
|
Hallo,
stimmt es, dass das expelezite euler verfahren nicht so genau ist und deswegen das runga kutta verfahren besser geeignet ist? Und kann ich mit den Thermen aus Schritt 14 und 19 rechnen? Ich brauche ja irgendeine Gleichung was soll ich dafür hernehmen? |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
 hansguckindieluft Verfasst am: 10. Sep 2016 14:03 Titel: hansguckindieluft Verfasst am: 10. Sep 2016 14:03 Titel: |
 |
|
Hallo,
das explizite Euler Verfahren ist das einfachste Verfahren. Es ist bei gleicher Schrittweite ungenauer als die Runge Kutta Verfahren. Letztere sind daher effizienter.
Mit dem Euler- Verfahren kann man aber mei entsprechend kleiner Schrittweite die gleiche Genauigkeit erhalten. Vielleicht macht es Sinn, erstmal damit zu starten.
Und ja, die Gl. 14 und 19 sind die beiden DGLs, welche das Doppelpendel beschreiben.
Vielleicht solltest Du aber erstmal ein einfaches Pendel numerisch lösen, um erste Erfahrungen zu sammeln. Das numerische Ergebnis kannst Du dann (bei kleiner Amplitude) mit dem analytischen Ergebnis vergleichen. So bekommst Du ein Gefühl dafür, wie gut die numerische Näherung ist.
Gruß |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 10. Sep 2016 15:53 Titel: Marina17 Verfasst am: 10. Sep 2016 15:53 Titel: |
 |
|
| hansguckindieluft hat Folgendes geschrieben: | Hallo,
Und ja, die Gl. 14 und 19 sind die beiden DGLs, welche das Doppelpendel beschreiben.
|
Wie kann ich diese zwei Gleichungen verwenden? Beim Eulerverfahren brauche ich doch immer eine Gleichung die eine Variable die ich rausfinden mag abgeleitet hat. |
|
 |
Marina17
Anmeldungsdatum: 22.08.2016
Beiträge: 19
|
 Marina17 Verfasst am: 11. Sep 2016 10:29 Titel: Marina17 Verfasst am: 11. Sep 2016 10:29 Titel: |
 |
|
Hallo,
mir ist noch was aufgefallen!!! Ich habe ja wenn ich so wie in meinen Link die Hamiltonfunktion anwende dann habe ich ja die Ableitung von den Beiden Winkel und danach eine Differentialgleichung. Im Link würde ich dann Gleichung 25 und 25 hernehmen. Stimmt das? |
|
 |
|















