| Autor |
Nachricht |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 14. Nov 2021 17:33 Titel: Teilchen und Gruppen Kelvin1995 Verfasst am: 14. Nov 2021 17:33 Titel: Teilchen und Gruppen |
 |
|
Hallo ich habe ein bisschen über Teilchen und Liegruppen gelesen, wobei ich mir ein wenig zusammengereimt habe, aber meine Vorstellungen noch vage sind.
Jedenfalls wollte ich mal fragen ob meine Vorstellungen richtig sind.
Also man hat z.B die Gruppe SO(3). Diese Gruppe kann man in natürlicherweise konstruieren indem man betrachtet wie die Elemente dieser Gruppe auf Vektoren des R³ wirken. Letztlich kann man die Elemente damit als 3x3 Matrizen darstellen.
Nun hat man es in der Quantenmechanik in der Regel mit Hilberträumen zu tun, weshalb man nach Darstellungen so einer Gruppe mit einem Hilbertraum als Darstellungsraum sucht. Letztlich sucht man also nach Operationen, die auf Elemente 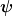 des Hilbertraums wirken und sie auf andere Elemente des Hilbertraums wirken und sie auf andere Elemente 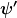 abgebildet werden sollen. Dabei sollen diese Operatoren bzgl ihrer Verkettung eine Gruppe mit denselben Verknüpfungsregeln bilden wie die vorige Gruppe SO3. abgebildet werden sollen. Dabei sollen diese Operatoren bzgl ihrer Verkettung eine Gruppe mit denselben Verknüpfungsregeln bilden wie die vorige Gruppe SO3.
Dabei gibt es kleinste, sogenannte irreduzible Darstellungen bei denen man auf einem Darstellungsraum mit kleinstmöglicher Dimension operiert.
Der Tangentialraum am neutralen Element der Gruppe SO3 bildet eine Liealgebra. Die Komponenten des Drehimpulsoperators bilden eine Basis dieser Liealgebra.
Die Elemente der Gruppe werden dann dargestellt als:
)
Das Betragsquadrat des Drehimpulsoperators bildet einen sogenannten Casimir-Operator. Man kann die irreduziblen Darstellen nach den Eigenwerten des Casimiroperators klassifizieren. Die Eigenwerte sind abzählbar und lassen sich mit einer Drehimpulsquantenzahl durchnummerieren.
für l=1/2 erhält man bspw eine zweidimensionale Darstellung. Die Elemente dieses Darstellungsraumes nennt man Pauli-Spinoren.
Macht man dasselbe für die Gruppe SU2 kommt man zu den Weyl-Spinoren und macht man das für die Gruppe  kommt man zu den Diracspinoren. kommt man zu den Diracspinoren.
Wobei ich mir da noch unsicher bin.
Bedeutet das also letztlich, dass das Ziel ist, die Poincaré-Gruppe über einen Hilbertraum darzustellen, so dass man Elemente eines Hilbertraums hat von denen man weiß wie sie unter einer Poincaré-Gruppe transformieren und man damit dann letztlich Poincaré-Invariante Lagrangedichten (und damit auch entsprechende Invariante Bewegungsgleichungen) konstruieren kann?
Ich habe sowas nicht studiert, sondern beschäftige mich nur hobbymäßig damit. Deshalb sorry wenn ich blöd nachfrage.
Lernt man sowas eigentlich regulär in einem Physikstudium oder ist das nur eine Teilmenge der Physiker, die sich damit auskennen sollte? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 14. Nov 2021 18:08 Titel: TomS Verfasst am: 14. Nov 2021 18:08 Titel: |
 |
|
So wir ich das sehe, hast du das korrekt dargestellt.
Mal eine kurze Zusammenfassung:
Man betrachtet Symmetriegruppen, z.B. die Poincaregruppe inklusive Translationen und Rotationen SO(3); die Gruppe U(1) der el.-mag. WW; die Gruppe SU(3) der Farbwechselwirkung der QCD u.a.m. Die Symmetrie besagt, dass erhaltene Ladungen existieren. Für die genannten Gruppen sind diese Ladungen Viererimpuls = (Energie E, Dreierimpuls P) und Drehimpuls L; die elektrische Ladung Q; die Farbladungen.
Die Ladung als Generatoren der Algebra liefern immer wieder die Gruppenoperation, so wie du das für den Drehimpuls und die Rotation beschrieben hast:

Die Ladungen verhalten sich genau so wie die ursprünglichen Matrizen. Wenn die Ladungen Q dem SU(2) Spin oder Isospin entsprechen, dann entsprechen die Matrizen t gerade 1/2 mal den Pauli-Matrizen. D.h.


Während die Matrizen rein algebraische Objekte darstellen, wirken die Ladungen Q und die Transformationen U auf dem Hilbertraum.
D.h. der Hilbertraum „zerfällt“ in Sektoren, die gerade den Multiplets der Algebra entsprechen; diese Multiplets sind im Falle der Lorentzgruppe gerade die Lorentzskalare, -spinoren, -vektoren etc.; im Falle der SU(3) Color sind dies die Quarks (fundamentale Darstellung), Gluonen (adjungierte Darstellung), Baryonen und Mesonen (triviale / skalare Darstellung).
D.h. die Casimir-Operatoren und die Eigenwerte der Ladungen Q führen auf die Darstellungen, die Transformationen U rotieren die Zustände im Hilbertraum (also die Richtung eines Drehimpulses oder die Farben im Farbraum).
Man lernt in der Quantenmechanik einiges zu der SU(2) und SO(3) für Spin und Drehimpuls, teilweise auch einiges zum Spin und der Poincaregruppe. Themen wie die Symmetrien der QCD lernt man aber nur in Spezialvorlesungen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 14. Nov 2021 22:54 Titel: Kelvin1995 Verfasst am: 14. Nov 2021 22:54 Titel: |
 |
|
Danke TomS,
| TomS hat Folgendes geschrieben: |
Man betrachtet Symmetriegruppen, z.B. die Poincaregruppe inklusive Translationen und Rotationen SO(3); die Gruppe U(1) der el.-mag. WW; die Gruppe SU(3) der Farbwechselwirkung der QCD u.a.m. Die Symmetrie besagt, dass erhaltene Ladungen existieren. Für die genannten Gruppen sind diese Ladungen Viererimpuls = (Energie E, Dreierimpuls P) und Drehimpuls L; die elektrische Ladung Q; die Farbladungen.
|
Welche Ladungen ergeben sich aus den Lorentz-Boosts?
Ist es üblich in diesem Kontext bzgl des Noether Theorems auch bei Impulse, Drehimpulse ... von Ladungen zu sprechen? Zumindest ist es erstmal ungewohnt von einem Drehimpuls als Ladung zu sprechen.
Nehmen wir mal an wir betrachten die SO(3) Gruppe in einer Darstellung mit einem Hilbertraum als Darstellungsraum und betrachten die irreduzible Darstellung für l=1. Also Pauli-Spinoren.

Wenn ich nun aber damit Teilchen beschreiben möchte, verwendet man ja in der Regel Felder. also sowas wie
 \right> = a(x) \left| up \right> + b(x) \left| down \right> )
weil ja ein teilchen nicht nur aus dem Spin besteht.
Man ordnet also jedem Punkt im Raum einen Spinor zu und hat dann sowas wie ein Spinorfeld.
Meine Frage ist nun wie man sowas formal auf einer Mannigfaltigkeit konstruiert. Wenn ich Tensoren konstruiere, verwendet man an jedem Punkt der Mannigfaltigkeit den entsprechenden Tangentialraum als Basis.
Wie konstruiert man entsprechend Spinorfelder? Es geht mir nur darum die grobe Idee zu verstehen.
Diesen wikipediaartikel versteh ich nicht. dazu fehlt mir wohl ein bisschen an Vorwissen:
en.wikipedia.org/wiki/Spinor_field |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 14. Nov 2021 22:55 Titel: Kelvin1995 Verfasst am: 14. Nov 2021 22:55 Titel: |
 |
|
|
Sorry ich meinte oben mit l=1/2 |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Nov 2021 08:57 Titel: TomS Verfasst am: 15. Nov 2021 08:57 Titel: |
 |
|
Für eine formale Konstruktion bin ich wohl der falsche Ansprechpartner :-(
Aber noch ein Punkt zur Notation:
In der klassischen Feldtheorie und der (relativistischen) Quantenmechanik transformieren Felder bzw. Wellenfunktionen gemäß der o.g. Darstellungen. Allerdings kann mittels eines abstrakten Hilbertraumes jeder Zustand als Ket geschrieben werden; die Wellenfunktionen sind lediglich Komponenten dieses Kets bzgl. einer bestimmten Basis.
In der Quantenfeldtheorie transformieren die Feldoperatoren (im wesentlichen so wie die klassischen Felder) gemäß der der o.g. Darstellungen, zusätzlich aber auch die Kets.
Der Witz ist jedoch, dass Transformationen immer mittels unitärer Operatoren dargestellt werden. Nehmen wir als Beispiel die QED und eine Rotation SO(3) als Untergruppe der Lorentzgruppe sowie Operatoren der elektromagnetischen Eichfelder A plus Spinoren psi.
Aus diesen konstruiert man die erhaltenen Ladungsoperatoren J bzgl. Rotation, also die Drehimpulse. Dies funktioniert mittels

Daraus folgen Rotationsoperatoren U mit Drehwinkeln theta

Alle Zustände und Feldoperatoren transformieren einheitlich gemäß



Aber für die Feldoperatoren resultiert daraus dann die bekannte Transformation
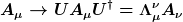
} \psi)
Lambda und S sind nun keine Operatoren mehr, sondern die bekannten rein algebraischen Matrizen der Lorentzgruppe, die natürlich zu den Drehwinkeln passen, also
)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 15. Nov 2021 09:55 Titel: Kelvin1995 Verfasst am: 15. Nov 2021 09:55 Titel: |
 |
|
Danke TomS
Ich wiederhole das nochmal, nur um zu vergewissern dass ich das richtig verstanden habe.
Es ist so, dass ich mir Drehungen im R^3 natürlich gut vorstellen kann. Das ist ja noch schön anschaulich. Hat es den Rang eines Postulats, dass sich bspw die kets entsprechend dieses unitären Operators transformieren, wenn ich im R^3 eine Drehung durchführe? Weil ich sehe nicht, dass man streng formal herleiten kann, dass bei einer Drehung des R^3 die kets sich so verhalten. Außer dass man halt den Hilbertraum als Darstellungsraum nimmt und die Teilchen dann in den Räumen der irreduziblen Darstellungen "leben". Aber dass sie in diesen Räumen leben ist eine Annahme oder?
Wenn das jedenfalls geklärt ist, betrachtet man die Erhaltungsgrößen nach dem Noether-Theorem. Diese Größen in Operatorform bilden dann die Erzeuger der Operatoren auf dem Hilbertraum.
Wenn man diese Operation identifiziert hat, sucht man den Casimir-Operator zu den Erzeugern und löst anschließend das Eigenwertproblem. Der Hilbertraum zerfällt in mehrere Darstellungsräume irreduzibler Darstellungen, die man mit den Eigenwerten des Casimir-Operators klassifizieren kann.
Die unterschiedlichen Teilchensorten leben dann in diesen Räume. Der Spin der Teilchen lässt sich mit den Eigenwerten des Casimir-Operators identifizieren. Bei halbzahligen Werten der entsprechenden Quantenzahl spricht man von Spinoren. Bei ganzzahligen Werten sind es Lorentz-Vektoren, außer bei der 0. Da sind es Skalare. Zumindest, wenn die zugrundeliegende Symmetrietransformation die Lorentzgruppe ist.
Ist das so richtig? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Nov 2021 10:49 Titel: TomS Verfasst am: 15. Nov 2021 10:49 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Hat es den Rang eines Postulats, dass sich bspw die kets entsprechend dieses unitären Operators transformieren, wenn ich im R^3 eine Drehung durchführe? |
Das folgt letztlich aus den Postulaten der Quantenmechanik.
Observablen bzw. die entsprechenden selbstadjungierten Operatoren wirken auf einem Hilbertraum.
Die hier betrachteten selbstadjungierten Operatoren sind gerade die erhaltenen Ladungen Q. Ihre Erhaltung folgt klassisch aus dem Noether-Theorem; in der Quantenmechanik entspricht dies einer Symmetrie des Hamiltonoperators bzw. der Heisenberg-Gleichung, d.h. beidemale [H,Q] = 0.
Diese erhaltenen Ladungen Q haben aber exakt die selben algebraischen Eigenschaften - insbs. Kommutatorrelationen - wie klassische Generatoren der Symmetrie, also die Basis der Lie-Algebra. D.h. die Ladungen sind eine Darstellung der Liealgebra. Das muss man nicht fordern, das ergibt sich automatisch aus der Konstruktion.
Anders herum: was anderes als diese unitären Operatoren soll denn auf den Vektoren eines Hilbertraumes wirken?
Sei ein separabler Hilbertraum gegeben. Auf diesem wirken Operatoren Q und U. Wie möchtest eine ganz normale Matrix wie eine Paulimatrix allgemein auf einem Hilbertraum wirken lassen? Das funktioniert erst sinnvoll, wenn du für diesen Hilbertraum eine spezielle Darstellung einführst, also z.B. zweikomponentige Spinoren betrachtest; vorher ist das sinnlos.
D.h. der Übergang von den unitären Operatoren U und den Kets zu irgendwelchen Matrizen und Wellenfunktionen (Skalare, Spinoren ...) entspricht jeweils der Wahl einer speziellen Darstellung. Leider wird das von vielen Physikern nie so erklärt, es wird immer mit den einzelnen Darstellungen hantiert.
| Kelvin1995 hat Folgendes geschrieben: | | Weil ich sehe nicht, dass man streng formal herleiten kann, dass bei einer Drehung des R^3 die kets sich so verhalten. Außer dass man halt den Hilbertraum als Darstellungsraum nimmt und die Teilchen dann in den Räumen der irreduziblen Darstellungen "leben". Aber dass sie in diesen Räumen leben ist eine Annahme oder? |
Es ist eine Konstruktion.
In der nicht-relativistischen Quantenmechanik ist das nicht so relevant, da man es fast ausschließlich immer mit der selben Art von Teilchen zu tun hat, und daher immer mit der selben Darstellung. Die Nutzung der Kets anstelle der Wellenfunktion
 = \langle x | \psi \rangle )
liefert eine etwas kompaktere Darstellung. In der Quantenfeldtheorie ist eine Notation mittels Wellenfunktionen (das wären übrigens korrekterweise ein Funktional über den Felder, nicht eine Funktion über Koordinaten) eine notationstechnische Katastrophe.
| Kelvin1995 hat Folgendes geschrieben: | Wenn das jedenfalls geklärt ist, betrachtet man die Erhaltungsgrößen nach dem Noether-Theorem. Diese Größen in Operatorform bilden dann die Erzeuger der Operatoren auf dem Hilbertraum.
Wenn man diese Operation identifiziert hat, sucht man den Casimir-Operator zu den Erzeugern und löst anschließend das Eigenwertproblem. Der Hilbertraum zerfällt in mehrere Darstellungsräume irreduzibler Darstellungen, die man mit den Eigenwerten des Casimir-Operators klassifizieren kann. |
Korrekt.
| Kelvin1995 hat Folgendes geschrieben: | Die unterschiedlichen Teilchensorten leben dann in diesen Räume. Der Spin der Teilchen lässt sich mit den Eigenwerten des Casimir-Operators identifizieren. Bei halbzahligen Werten der entsprechenden Quantenzahl spricht man von Spinoren. Bei ganzzahligen Werten sind es Lorentz-Vektoren, außer bei der 0. Da sind es Skalare. Zumindest, wenn die zugrundeliegende Symmetrietransformation die Lorentzgruppe ist.
Ist das so richtig? |
So ziemlich.
Nehmen wir das Beispiel die SU(2).
Ein zweikomponentiges Feld mit geeigneten Transformationseigenschaften wird als Spinor bzw. Spinorfeld bzgl. der SU(2) bezeichnet.
 \to e^{iS(\Lambda)} \, \psi(x))
Aber auch der Ket ist in gewisser Weise ein Spinor. Er ist zwar kein Feld, aber er transformiert exakt so wie ein Spinor. Es gilt
 = \langle x | \psi \rangle)

Dabei gilt in allen Fällen die Gruppeneigenschaft, d.h.

} \cdot e^{iS(\Lambda_2)} = e^{iS(\Lambda_3)} )

Und damit "ist" der Ket formal ein Spinor.
Spinoren sind im einfachsten Fall Darstellungen der SU(2); die Drehimpuls-Eigenwerte sind

Die 0 entspricht der trivialen (skalaren) Darstellung. Die halbzahligen Darstellungen sind die Spinordarstellungen. Die ganzzahligen entsprechen den Vektoren (l = 1) sowie höheren Tensoren (l = 2 ...).
Die Darstellungen der SO(3) lauten übrigens

d.h. die SO(3) liefert eine Untermenge der Darstellungen der SU(2).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 15. Nov 2021 11:11 Titel: Kelvin1995 Verfasst am: 15. Nov 2021 11:11 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Diese erhaltenen Ladungen Q haben aber exakt die selben algebraischen Eigenschaften - insbs. Kommutatorrelationen - wie klassische Generatoren der Symmetrie, also die Basis der Lie-Algebra. D.h. die Ladungen sind eine Darstellung der Liealgebra. Das muss man nicht fordern, das ergibt sich automatisch aus der Konstruktion.
|
Heißt das man stellt fest, dass die klassischen Matrizen der Liealgebra (im Falle von Drehungen) dieselben Kommutatorrelationen erfüllen wie die Drehimpulsoperatoren und deshalb identifiziert man die Drehimpulsoperatoren als die Generatoren?
Ist das so, weil in beiden Fällen dieselbe Liealgebra produziert wird, da schließlich die Lieklammer mehr oder weniger identisch ist?
Dann müsste man doch allgemein zeigen können, dass die durch das Noether-Theorem erhaltenen Ladungsoperatoren dieselben Kommutatorrelationen erfüllen wie die entsprechenden klassischen Matrizen oder? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Nov 2021 11:11 Titel: TomS Verfasst am: 15. Nov 2021 11:11 Titel: |
 |
|
Kleine Übung, um den Zusammenhang zwischen den Matrix-Darstellungen und den Operatoren zu verstehen:
Schau dir mal den N-dim. harmonischen Oszillator mit den Erzeugungs- und Vernichtungsoperatoren an.
Diese erfüllen


mit i,k = 1 ... N.
Gegeben seien die Generatoren T der SU(N), d.h. es gelte

mit a, b, c = 1 ... N²-1.
Definiere

_{ik} a_k)
(a nummeriert die Matrizen; i,k nummeriert die Matrixelemente je a)
Zu zeigen ist:


Damit sieht man sofort, dass der N-dim. harmonische Oszillator eine SU(N) Symmetrie aufweist, und dass die Eigenzustände von H (= die Lösungen des N-dim. harmonischen Oszillators) gemäß der Multipletts der SU(N) klassifiziert werden können.
Interessanterweise ist die SU(N) eine viel größere Symmetrie als die SO(N).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Nov 2021 11:20 Titel: TomS Verfasst am: 15. Nov 2021 11:20 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Heißt das man stellt fest, dass die klassischen Matrizen der Liealgebra (im Falle von Drehungen) dieselben Kommutatorrelationen erfüllen wie die Drehimpulsoperatoren und deshalb identifiziert man die Drehimpulsoperatoren als die Generatoren? |
Ja (ich würde nicht "identifiziert" sagen, denn es sind Generatoren unterschiedlicher Darstellungen)
| Kelvin1995 hat Folgendes geschrieben: | | Ist das so, weil in beiden Fällen dieselbe Liealgebra produziert wird, da schließlich die Lieklammer mehr oder weniger identisch ist? |
Ja; und sie ist exakt identisch.
| Kelvin1995 hat Folgendes geschrieben: | | Dann müsste man doch allgemein zeigen können, dass die durch das Noether-Theorem erhaltenen Ladungsoperatoren dieselben Kommutatorrelationen erfüllen wie die entsprechenden klassischen Matrizen oder? |
Ja, das kann man auch (bis auf sehr spezielle Ausnahmen, die wir besser mal zurückstellen)
Der Startpunkt ist dabei bereits die klassische Mechanik oder die klassische Feldtheorie in der hamiltonschen Formulierung sowie insbs. die Poissonklammer {.,.}, die im Zuge der Quantisierung durch den Kommutator i[.,.] ersetzt wird. D.h. die Lie-Algebra für die erhaltenen Ladungen folgt bereits mittels der klassischen Poissonklammer für die klassischen Objekte. Der klassische kanonische Formalismus wird (für diese algebraischen Eigenschaften) sozusagen bijektiv in den quantenmechanischen Formalismus überführt; hinzu kommt noch der Hilbertraum, auf dem die Operatoren wirken.
Wenn also der Drehimpuls erhalten ist, dann gilt klassisch bzw. quantenmechanisch


_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 15. Nov 2021 11:38, insgesamt einmal bearbeitet |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 15. Nov 2021 11:38 Titel: Kelvin1995 Verfasst am: 15. Nov 2021 11:38 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Zu zeigen ist:


Damit sieht man sofort, dass der N-dim. harmonische Oszillator eine SU(N) Symmetrie aufweist, und dass die Eigenzustände von H (= die Lösungen des N-dim. harmonischen Oszillators) gemäß der Multipletts der SU(N) klassifiziert werden können.
Interessanterweise ist die SU(N) eine viel größere Symmetrie als die SO(N). |
Meine Fragen dazu wären noch.
Ist die Konstruktion der  eindeutig? Ich vermute mal nein. eindeutig? Ich vermute mal nein.
Die zweite Frage ist wie ich systematisch die  konstruieren kann, wenn ich sie noch nicht kenne. Bei einer gegebenen Konstruktion ist es natürlich leicht zu zeigen, dass die Kommutatorrelationen erfüllt sind. konstruieren kann, wenn ich sie noch nicht kenne. Bei einer gegebenen Konstruktion ist es natürlich leicht zu zeigen, dass die Kommutatorrelationen erfüllt sind.
Die Erwähnung der Poisson-Klammer hat mir sehr geholfen. Damit habe ich schonmal die Verbindung zur klassischen Physik bekommen.
Aber wie sähe dann klassisch so eine Transformation mit Generatoren aus?
also sowas wie
) wäre dann ja klassisch einfach eine Funktion und das würde ja nicht auf etwas wirken wäre dann ja klassisch einfach eine Funktion und das würde ja nicht auf etwas wirken
Oder setzt man die Orte in die Ls ein und U gibt dann den gedrehten Ortsvektor? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Nov 2021 11:42 Titel: TomS Verfasst am: 15. Nov 2021 11:42 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Ist die Konstruktion der  eindeutig? Ich vermute mal nein. eindeutig? Ich vermute mal nein. |
Bis auf SU(N)-Rotationen (und weitere damit zusammenhängende diskrete Transformationen) ist sie eindeutig.
| Kelvin1995 hat Folgendes geschrieben: | Die zweite Frage ist wie ich systematisch die  konstruieren kann, wenn ich sie noch nicht kenne. Bei einer gegebenen Konstruktion ist es natürlich leicht zu zeigen, dass die Kommutatorrelationen erfüllt sind. konstruieren kann, wenn ich sie noch nicht kenne. Bei einer gegebenen Konstruktion ist es natürlich leicht zu zeigen, dass die Kommutatorrelationen erfüllt sind. |
Um mehr geht es zunächst nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 15. Nov 2021 20:52 Titel: Kelvin1995 Verfasst am: 15. Nov 2021 20:52 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Die Darstellungen der SO(3) lauten übrigens

d.h. die SO(3) liefert eine Untermenge der Darstellungen der SU(2). |
In diesem Skript
uni-muenster.de/Physik.TP/archive/fileadmin/lehre/teilchen/ss13/SO3SU2.pdf
wurden die Darstellungen der SO(3) hergeleitet, aber es gibt da keinen Grund warum die Drehimpulsquantenzahlen nicht halbzahlig sein dürfen. Auf Seite 12 heißt es weiter:
| Zitat: | | Für j=1/2 gibt es eine zweidimensionale Darstellung ... |
Die zugehörigen Matrizen werden dann zwar als Erzeugende der SU(2) identifiziert, jedoch ist dies dann ja auch eine Darstellung des SO(3) über einen Hilbertraum. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 15. Nov 2021 20:57 Titel: Kelvin1995 Verfasst am: 15. Nov 2021 20:57 Titel: |
 |
|
Eigentlich müssten doch alle Drehgruppen mit der gleichen Anzahl an Parametern zu denselben Darstellungen führen oder nicht?
SO(3) und SU(2) haben beide 3 Parameter.
Damit haben sie beide drei Operatoren, die alle jeweils dieselben Kommutatorrelationen erfüllen und damit derselben Algebra genügen, so dass sie zu den selben Darstellungen führen müssen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Nov 2021 22:57 Titel: TomS Verfasst am: 15. Nov 2021 22:57 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | … wurden die Darstellungen der SO(3) hergeleitet, aber es gibt da keinen Grund warum die Drehimpulsquantenzahlen nicht halbzahlig sein dürfen. Auf Seite 12 heißt es weiter:
| Zitat: | | Für j=1/2 gibt es eine zweidimensionale Darstellung ... |
Die zugehörigen Matrizen werden dann zwar als Erzeugende der SU(2) identifiziert, jedoch ist dies dann ja auch eine Darstellung des SO(3) über einen Hilbertraum. |
Das ist falsch.
Die SO(3) liefert keine Darstellung mit l = 1/2, da dies zwingend unitäre und insbs. komplexe Gruppenelemente erfordert, die auf einem komplexen Hilbertraum wirken. Die SO(3) ist aber definiert mittels reeller orthogonaler Matrizen, die auf einem reellen Hilbertraum wirken.
| Kelvin1995 hat Folgendes geschrieben: | Eigentlich müssten doch alle Drehgruppen mit der gleichen Anzahl an Parametern zu denselben Darstellungen führen oder nicht?
SO(3) und SU(2) haben beide 3 Parameter.
Damit haben sie beide drei Operatoren, die alle jeweils dieselben Kommutatorrelationen erfüllen und damit derselben Algebra genügen, so dass sie zu den selben Darstellungen führen müssen. |
Du vergisst, wie die Gruppen definiert sind. Die SO(3) ist definiert als Gruppe orthogonaler Matrizen mit reellen Elementen und Determinante Eins:
: g_{ik} \in \mathbb{R} \wedge g g^t = g^t g = 1)
Die SU(2) enthält jedoch unitäre Matrizen mit komplexen Elementen und Determinante Eins:
: g_{ik} \in \mathbb{C} \wedge g g^\dagger = g^\dagger g = 1)
D.h. die SO(3) ist eine echte Untergruppe der SU(2).
Außerdem gibt es speziell in diesem Fall eine Abbildung
 \to SO(3))
die jedoch nicht bijektiv sondern 2 zu 1 ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 16. Nov 2021 17:05, insgesamt 2-mal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Nov 2021 09:33 Titel: index_razor Verfasst am: 16. Nov 2021 09:33 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Die zugehörigen Matrizen werden dann zwar als Erzeugende der SU(2) identifiziert, jedoch ist dies dann ja auch eine Darstellung des SO(3) über einen Hilbertraum. |
Du kannst von der Algebra allein nicht auf die Darstellungen der Gruppe schließen. Hier spielen auch globale topologische Eigenschaften der Gruppe eine Rolle. Die Generatoren definieren im allgemeinen nur die projektiven unitären Darstellungen, also solche Abbildungen auf unitäre Operatoren, die dem Multiplikationsgesetz
U(h) = e^{i\phi(g,h)}U(gh))
genügen. Die zusätzliche Frage lautet dann also noch unter welchen Voraussetzungen man die Phasenfaktoren eliminieren kann, so daß man eine echte Darstellung erhält. Für einfach zusammenhängende Gruppen wie SU(2) geht das immer. Bei der SO(3) aber nicht.
Zuletzt bearbeitet von index_razor am 17. Nov 2021 10:41, insgesamt 2-mal bearbeitet |
|
 |
cn
Anmeldungsdatum: 15.11.2021
Beiträge: 3
|
 cn Verfasst am: 16. Nov 2021 10:13 Titel: cn Verfasst am: 16. Nov 2021 10:13 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
D.h. die SO(3) ist eine echte Untergruppe der SU(2).
Außerdem gibt es speziell in diesem Fall eine Abbildung
 \to SO(3))
|
Vielleicht hast du gemeint, dass die SO(3) eine echte Untergruppe der SU(3) ist, und nicht SU(2). Soweit ich weiß, ist SO(3) nicht eine natürliche Untergruppe der SU(2). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 16. Nov 2021 17:15 Titel: TomS Verfasst am: 16. Nov 2021 17:15 Titel: |
 |
|
Nein, ich habe tatsächlich die SO(3) gemeint.
Es geht auch nicht darum, dass SO(3) eine Untergruppe der SU(2) wäre, sondern dass die SU(2) die Überlagerungsgruppe der SO(3) ist und beide lokal isomorph sind.
https://www.pas.rochester.edu/assets/pdf/undergraduate/su-2s_double_covering_of_so-3.pdf
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Nov 2021 12:49 Titel: Re: Teilchen und Gruppen index_razor Verfasst am: 17. Nov 2021 12:49 Titel: Re: Teilchen und Gruppen |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
für l=1/2 erhält man bspw eine zweidimensionale Darstellung. Die Elemente dieses Darstellungsraumes nennt man Pauli-Spinoren.
Macht man dasselbe für die Gruppe SU2 kommt man zu den Weyl-Spinoren und macht man das für die Gruppe  kommt man zu den Diracspinoren. kommt man zu den Diracspinoren. |
Ich denke die Gruppe SU(2) x SU(2) hat nichts speziell mit Diracspinoren zu tun. Es geht in allen Fällen immer um Darstellungen der eigentlichen Lorentzgruppe, bzw. deren Überlagerungsgruppe SL(2,C) (oder der SU(2), im Zusammenhang mit dem Spin). Die Generatoren dieser Gruppen betrachtet man immer als Elemente einer komplexen Lie-Algebra. Das gilt sowohl für die Darstellungen der su(2) (die werden ja normalerweise mit Hilfe der Leiteroperatoren  analysiert), als auch für die Generatoren der Lorentzgruppe. Insbesondere bei letzterer verwendet man komplexe Linearkombination von Drehimpuls und Boostgeneratoren, um die komplexe Lorentzalgebra mit einer Summe su(2) + su(2) zu identifizieren. analysiert), als auch für die Generatoren der Lorentzgruppe. Insbesondere bei letzterer verwendet man komplexe Linearkombination von Drehimpuls und Boostgeneratoren, um die komplexe Lorentzalgebra mit einer Summe su(2) + su(2) zu identifizieren.
Ich vermute so kommen in diesem Zusammenhang die beiden Kopien der SU(2) ins Spiel, auf die du dich hier vielleicht beziehst. Aber das ist unabhängig von der Art von Teilchen/Feldern. Es geht immer um dieselben Gruppen (SU(2), SL(2,C),...), lediglich um unterschiedliche Darstellungen davon. |
|
 |
|
|















