| Autor |
Nachricht |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 07. Aug 2021 23:08 Titel: Schwarzes Loch und Schwarzschildradius schnudl Verfasst am: 07. Aug 2021 23:08 Titel: Schwarzes Loch und Schwarzschildradius |
 |
|
Ein frei fallender Körper, der sich radial einem Schwarzen Loch SL nähert erreicht dessen Schwarzschildradius Rs im Koordinatensystem des ruhenden SL (Koordinaten r und t der Schwarzschild Metrik) bekanntlich nie, da die Geschwindigkeit dr/dt in diesen Koordinaten r=Rs Null wird. Das ist, soweit ich gelesen habe ein reines Artifakt der Metrik.
Ich habe aber nie verstanden, wie es sein kann, dass ein Körper dann überhaupt in das schwarze Loch fallen kann: Wenn man sich vorstellt, dass in verschiedenen Abständen r>= Rs Beobachter positioniert sind, die den Zeitpunkt notieren, zu dem der Körper gerade bei ihnen vorbei fliegt, dann würde der Beobachter bei r=Rs NIE etwas notieren, da die Geschwindigkeit dort zum Erliegen kommt. Wie kann es dann aber sein, dass ein mitfliegender Beobachter in seiner Eigenzeit davon 'nichts merkt" und den Innenraum r<Rs mühelos erreicht?
Ich verstehe das zwar "so leidlich" von der mathematischen Seite, aber kann mir unter dieser bizarren Situation nichts mehr vorstellen: Wenn nämlich ein fliegender Beobachter in seiner Lebenszeit (Eigenzeit) das Innere erreicht, wie kann es dann sein, dass im ruhenden Koordinatensytem niemals das Ereignis r=Rs zu einem endlichen t eintritt? Dieses "t" ist ja schließlich für den ruhenden Beobachter seine "normale" Zeit (ist das so?) und ich würde naiverweise erwarten, dass der Körper irgendwann bei einem bei r=Rs stationierten Beobachter vorbeikommt und dieser das Ereignis erlebt.
Leider habe ich hier einen totalen Knoten im Kopf. Wie kann man dieses Paradox auflösen?(
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Aug 2021 09:41 Titel: index_razor Verfasst am: 08. Aug 2021 09:41 Titel: |
 |
|
Das Paradoxon entsteht ja eigentlich nur dadurch, daß du von einem stationären Beobachter am Schwarzschildradius ausgehst. Sowas ist genauso wenig möglich wie ein Beobachter, der sich mit Lichtgeschwindigkeit bewegt. An jedem äußeren Beobachter ( ) kommt das Teilchen ja nach endlichem t vorbei. ) kommt das Teilchen ja nach endlichem t vorbei.
Für andere Ereignisse ist das spezielle Koordinatensystem ) einfach nicht zuständig. Die Frage "wie kann es dann sein, dass im ruhenden Koordinatensytem niemals das Ereignis r=Rs zu einem endlichen t eintritt?" ist vergleichbar mit der Frage wie es möglich sein kann den Nordpol zu erreichen, wenn er in stereographischer Projektion im Unendlichen liegt. Genau das ist ja mit "Koordinatenartefakt" gemeint. Die Koordinaten sagen dir überhaupt nicht, was am Schwarzschildradius passiert. einfach nicht zuständig. Die Frage "wie kann es dann sein, dass im ruhenden Koordinatensytem niemals das Ereignis r=Rs zu einem endlichen t eintritt?" ist vergleichbar mit der Frage wie es möglich sein kann den Nordpol zu erreichen, wenn er in stereographischer Projektion im Unendlichen liegt. Genau das ist ja mit "Koordinatenartefakt" gemeint. Die Koordinaten sagen dir überhaupt nicht, was am Schwarzschildradius passiert.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 08. Aug 2021 12:38 Titel: schnudl Verfasst am: 08. Aug 2021 12:38 Titel: |
 |
|
Hmmm...du hast sicher recht, aber verinnerlichen kann ich das noch nicht. Die Spur eines Flugzeugs, das über den Nordpol fliegt, wird in der stereografischen Projektion ja immer schneller und "flippt" dann auf die andere Seite. Das Flugzeug passiert den Nordpol also auch in diesen Koordinaten. Beim Schwarzen Loch tritt das aber nie ein.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Aug 2021 13:21 Titel: index_razor Verfasst am: 08. Aug 2021 13:21 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | | Hmmm...du hast sicher recht, aber verinnerlichen kann ich das noch nicht. Die Spur eines Flugzeugs, das über den Nordpol fliegt, wird in der stereografischen Projektion ja immer schneller und "flippt" dann auf die andere Seite. Das Flugzeug passiert den Nordpol also auch in diesen Koordinaten. Beim Schwarzen Loch tritt das aber nie ein. |
Doch, etwas völlig analoges tritt beim Fall ins Schwarze Loch ein. Du stellst lediglich die falschen Größen einander gegenüber. Dem endlichen Abstand bis zum Nordpol entspricht die endliche Eigenzeit des einfallenden Beobachters bis zum Erreichen des Horizonts. Beides sind koordinatenunabhängige metrische Größen. Dieser endliche Abstand entspricht in beiden Fällen einer unendlichen Koordinatendifferenz -- der projektiven Koordinaten für die Sphäre, der Koordinate t in der Schwarzschildraumzeit. Beides hängt unmittelbar damit zusammen, daß die jeweiligen Koordinaten, nicht den gesamten Raum (Raumzeit) überdecken.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Aug 2021 00:30 Titel: schnudl Verfasst am: 10. Aug 2021 00:30 Titel: |
 |
|
Ich habe mich da noch ein wenig schlau gemacht und dabei bei der Lektüre eines Buches (Ray-Dinverno) auf die Kruskal-Szekeres-Koordinaten gestoßen: Diese umgehen das Abbildungsproblem.
Soweit ich verstanden habe werden hier neue hyperbolische Koordinaten u und v eingeführt, die man anstatt von r und t heranzieht, um die Metrik zu beschreiben:
)
)

für r>1
)
)

für r<1
mit einem ρ, das quasi den Abstand vom Schwarzschildradius angibt
Wie man auf sowas kommt sei mal dahingestellt, aber man kommt dadurch auf eine hyperbolische Metrik wie im Bild. t/2 entspricht einem hyperbolischen Winkel und ρ dem Radius in hyperbolischen polarkoordinaten. Die Geraden am Lichtkegel entsprechen dabei t=∞, die u-Achse t=0.
Innerhalb des Lichtkegels dreht sich der alles um, da das Vorzeichen von ρ wechselt. Soweit erscheint mir das völlig nachvollziehbar.
Wenn ich jetzt ein einfallendes Teilchen betrachte, so startet dieses vom roten Punkt bei einem bestimmten r und t=0.
Es erreicht den Schwarzschildradius ρ=0 nach unendlich langer Zeit (oranger Punkt).
Nun läuft es innerhalb des Ereignishorizonts weiter nach r=0 (bzw ρ=1) um am grünen Punkt final zu landen.
Wenn ich die obigen Transformationen ernst nehme, dann entspricht dem grünen Punkt aber wieder ein endliches t, denn die "Singularitätslinie" liegt nicht am Lichtkegel und nur dort ist t=∞.
Wie ist das zu interpretieren? Ich kann mir ungefähr vorstellen, wie man in den neuen Koordinaten die Weltinie eines einfallenden Teilchens ausrechnet; diese ist stetig in den neuen Koordinaten und geht vom Anfangspunkt bei t=0 zu einem Endpunkt bei einem endlichen t. Ich dachte mir aber aufgrund der ursprünglichen Betrachtungsweise in den Schwarzschild Koordinaten, dasses keinen sinn macht, nach dem Vorgang im inneren des Ereignishorizonts zu fragen. Nun sieht es aber so aus, als wäre der Zeitpunkt t, zu dem die Endposition in der Singularität erreicht wird sehr wohl definiert - nämlich über diese Transformation...
Ich drehe mich irgendwie im Kreis und es zerreißt mir mittlerweile den Schädel... 
Zumindest ist mir aber erstmals intuitiv klar geworden, warum ein Signal vom Teilchen, das sich innerhalb des Ereignishorizonts bewegt diesen niemals verlassen kann (Lichtkegel), umgekehrt aber Signale von außerhalb des Horizonts empfangen kann.
| Beschreibung: |
|

Download |
| Dateiname: |
kruskall_coordinates.JPG |
| Dateigröße: |
144.5 KB |
| Heruntergeladen: |
102 mal |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Aug 2021 08:07 Titel: index_razor Verfasst am: 10. Aug 2021 08:07 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: |
Wenn ich die obigen Transformationen ernst nehme, dann entspricht dem grünen Punkt aber wieder ein endliches t, denn die "Singularitätslinie" liegt nicht am Lichtkegel und nur dort ist t=∞.
Wie ist das zu interpretieren?
|
Bei der Annäherung an den Horizont geht t gegen unendlich. Das gilt sowohl für die Annäherung von Außen als auch von Innen. Auf der Weltlinie des Teilchens steigt t also im Außenbereich bis unendlich an und nach dem Überqueren des Horizonts fällt es von unendlich wieder ab. Das ist genau das Phänomen, das du beim Überqueren des Nordpols als "flippen" der projektiven Koordinate bezeichnet hast.
Man kann t im Innneren also schon verwenden, allerdings ist es dort keine Zeitkoordinate mehr. Das kann man schon daran sehen, daß 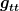 für für  das Vorzeichen wechselt. das Vorzeichen wechselt.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Aug 2021 09:00 Titel: schnudl Verfasst am: 10. Aug 2021 09:00 Titel: |
 |
|
Ich muss mich glaube ich vom Gedanken verabschieden, dass das Koordinatensystem der Schwarzschild-Metrik ein solches ist, wo ich mit einem Lineal/Uhr direkt physikalische Entfernungen ablesen kann. An einer stereographisch verzerrten Projektion kann ich das ja auch nicht, außer ich betrachte nur ein kleines Stück, wo der Raum "lokal flach" ist und ein Euklidisches Koordinatensystem existiert. Würde ich eine radiale Distanz entlang eines Schwarzen Lochs mit dem Lineal auslegen, würde ich nicht etwas messen, was mit "r" zusammenpasst. Stattdessen müsste ich die Eigenlängen/Zeiten in meinem lokalen Koordinatensystem aufintegrieren. Sehe ich das wenigstens halbwegs richtig?
Jetzt habe ich noch eine Frage: Ein Ereignishorizont entsteht ja immer dann, wenn die Masse eines Objekts innerhalb eines Radius eine gewisse Größe übersteigt. Wenn ein Stern auf ein paar km zusammenschrumpft und sein Durchmesser unter dem Schwarzschildradius der Masse liegt, dann entsteht ein Ereignishorizont und damit auch ein schwarzes Loch. Dieser Vorgang ist aus der Sicht der innenliegenden Materie aber nichts spektakuläres. Habe ich das richtig verstanden ?
Ich sehe in dieser primitiven Betrachtungsweise aber (noch) keine Notwendigkeit, dass es innerhalb eines Schwarzen Lochs eine Singularität bei r=0 geben müsse, wo sich alle Masse auf einen Punkt konzentriert. Es wird ein 1/r Potenzial angenommen, aber sobald man in einen radialen Körper eindringt, haben wir ja kein 1/r Gesetz mehr, da nur die Masse innerhalb des betrachteten Radius zählt. Dieses Szenario wird aber nicht betrachtet. Wieso kann man also sagen, dass ein Körper, der in den Ereignishorizont eindringt dazu verdammt ist, eine Reise nach r=0 zu starten um letztlich unweigerlich in einer Singularität zu enden? ist diese Singularität real oder bloß ein mathematisches Artifakt, das sich aus der Annahme einer Punktmasse ergibt?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
 DrStupid Verfasst am: 10. Aug 2021 09:46 Titel: DrStupid Verfasst am: 10. Aug 2021 09:46 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | | Es wird ein 1/r Potenzial angenommen, aber sobald man in einen radialen Körper eindringt, haben wir ja kein 1/r Gesetz mehr, da nur die Masse innerhalb des betrachteten Radius zählt. |
Das ist bestenfalls während der Entstehung des SL interessant. Wenn ein Beobachter in ein existierendes SL hinein fällt, wird er keine Gelegenheit haben, in das Innere einer dort exisitierenden Masseverteilung einzudringen, weil sie kollabiert, bevor er sie erreicht.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Aug 2021 10:20 Titel: schnudl Verfasst am: 10. Aug 2021 10:20 Titel: |
 |
|
heißt das jetzt, dass alle schwarzen löcher tatsäclich unendliche Dichte in einem Punkt haben? Ist das nicht unphysikalisch? Und warum MUSS ein SL zu einem Punkt kollabieren?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Aug 2021 11:19 Titel: index_razor Verfasst am: 10. Aug 2021 11:19 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | heißt das jetzt, dass alle schwarzen löcher tatsäclich unendliche Dichte in einem Punkt haben? Ist das nicht unphysikalisch?
|
Das ist genauso unphysikalisch wie unendliche Ladungsdichte und Selbstenergie eines geladenen Punktteilchens. Oft werden diese Divergenzen als Hinweise darauf verstanden, daß die Theorien, aus denen sie folgen, die Effekte auf kleinen Skalen nicht in zutreffend beschreiben.
| Zitat: | | Und warum MUSS ein SL zu einem Punkt kollabieren? |
Aus demselben Grund aus dem ein einfallender Beobachter nach Überqueren des Horizonts der (Vakuum-)Schwarzschildlösung nicht vermeiden kann in die Singularität zu stürzen. Es gibt einfach keine andere stationäre Lösung. Jegliche Materie muß einer zeitartigen Weltlinie folgen. Keine Zustandsgleichung mit noch so hohem Druck kann daran etwas ändern. Außerhalb der Materieverteilung stimmen nun alle möglichen Lösungen mit der Schwarzschildlösung überein. Aus dem Kruskaldiagram kann man aber direkt ablesen, daß innerhalb des Horizonts alle zeitartigen Weltlinien auf der Singularität enden. Unterschreitet die Ausdehnung der Materie also den Schwarzschildradius, hält nichts mehr den Kollaps auf.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Aug 2021 11:59 Titel: index_razor Verfasst am: 10. Aug 2021 11:59 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | Ich muss mich glaube ich vom Gedanken verabschieden, dass das Koordinatensystem der Schwarzschild-Metrik ein solches ist, wo ich mit einem Lineal/Uhr direkt physikalische Entfernungen ablesen kann. An einer stereographisch verzerrten Projektion kann ich das ja auch nicht, außer ich betrachte nur ein kleines Stück, wo der Raum "lokal flach" ist und ein Euklidisches Koordinatensystem existiert. Würde ich eine radiale Distanz entlang eines Schwarzen Lochs mit dem Lineal auslegen, würde ich nicht etwas messen, was mit "r" zusammenpasst. Stattdessen müsste ich die Eigenlängen/Zeiten in meinem lokalen Koordinatensystem aufintegrieren. Sehe ich das wenigstens halbwegs richtig?
|
Ja, die geometrische Bedeutung von r ist nicht der Eigenabstand bis zum Zentrum, sondern
}{4\pi}.)
Wegen der Krümmung des Raumes stimmt der Zusammenhang zwischen Flächeninhalt und "Radius" (also Eigenabstand) eben nicht mehr mit dem im flachen Raum überein.
| Zitat: |
Jetzt habe ich noch eine Frage: Ein Ereignishorizont entsteht ja immer dann, wenn die Masse eines Objekts innerhalb eines Radius eine gewisse Größe übersteigt. Wenn ein Stern auf ein paar km zusammenschrumpft und sein Durchmesser unter dem Schwarzschildradius der Masse liegt, dann entsteht ein Ereignishorizont und damit auch ein schwarzes Loch. Dieser Vorgang ist aus der Sicht der innenliegenden Materie aber nichts spektakuläres. Habe ich das richtig verstanden ?
|
Kommt vielleicht darauf an, was du als "spektakulär" betrachtest. In der Nähe des Horizonts treten schon ein paar merkwürdige Effekte auf.
| Zitat: |
ist diese Singularität real oder bloß ein mathematisches Artifakt, das sich aus der Annahme einer Punktmasse ergibt? |
Ob sie real ist, weiß keiner so genau. Aber sie folgt nicht lediglich aus der Annahme einer Punktmasse. Die Singularität tritt im Zuge des Gravitationskollaps in der ART unter recht allgemeinen Bedingungen auf und ist meines Wissens auch weitgehend unabhängig von der initialen Materieverteilung.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Aug 2021 12:39 Titel: schnudl Verfasst am: 10. Aug 2021 12:39 Titel: |
 |
|
Wenn ein Stern unter den Radius seines Schwarzschildradius schrumpft, dann ist seine Ausdehnung im ersten Moment noch endlich. Dann ist seine Masse sagen wir m=1 und sein Schwarzschildradius Rs ebenfalls 1.
Wenn ich mir nun eine Kugel im Inneren vorstelle mit r=1/2, dann hat diese Kugel die Masse 1/8 (homogene Dichte vorausgesetzt). Der Schwarzschildradius dieser inneren Masse ist somit 1/8 und liegt somit weit unter 1/2. Ich würde mir naiv erwarten, dass die Gravitation abnimmt, wenn man weiter in das Innere vordringt, so wie ja bei der Newton'schen Gravitation nur das Innere der Umrandung zählt. Wahrscheinlich ist dies hier aber falsch...
Aber was wäre, wenn es sich im im Extremfall um eine Hohlkugel handelte? Dann müsste ja ihr Hohlraum feldfrei sein und der Raum dort "flach" ? Ein Teilchen würde dann ja auch nicht in den Hohlraum bis ins Zentrum fallen - oder etwa doch? Das ist meine "Überlegung" von oben auf die Spitze getrieben.
Aber ich sehe natürlich schon: man kann nicht über Schwarze Löcher reden, solange man die Theorie nicht beherrscht. Leider liegt das für mich aber alles in unerreichbarer Ferne und so kann ich leider nur an den grundlegendsten Dingen teilhaben...
Dennoch danke für die Antworten... 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
 DrStupid Verfasst am: 10. Aug 2021 13:01 Titel: DrStupid Verfasst am: 10. Aug 2021 13:01 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | | Wenn ich mir nun eine Kugel im Inneren vorstelle mit r=1/2, dann hat diese Kugel die Masse 1/8 (homogene Dichte vorausgesetzt). Der Schwarzschildradius dieser inneren Masse ist somit 1/8 und liegt somit weit unter 1/2. Ich würde mir naiv erwarten, dass die Gravitation abnimmt, wenn man weiter in das Innere vordringt, so wie ja bei der Newton'schen Gravitation nur das Innere der Umrandung zählt. |
Der Betrag der Newtonschen Gravitationskraft nimmt ab. Der Betrag des Newtonschen Gravitationspotentials nimmt zu. Newton stimmt hier zwar nicht mehr, aber die Tendenz sollte trotzdem stimmen.
Das spielt für einen Beobachter, der von außen hinein fällt, aber keine Rolle, weil er die kollabierende Masseverteilung erst im Zentrum erreicht. Bis dahin befindet er sich außerhalb der Verteilung und da ist das Newtonsche Gravitationsfeld einer kugelsymmetrischen Masseverteilung nicht von dem einer gleich schweren Punktmasse zu unterscheiden.
Ein Beobachter, der sich von Anfang an im Inneren der Masseverteilung befindet, kollabiert mit ihr gemeinsam zur Singularität.
| schnudl hat Folgendes geschrieben: | | Aber was wäre, wenn es sich im im Extremfall um eine Hohlkugel handelte? |
Dasselbe in grün. Ein außenstehender Beobachter kann die Hohlkugel nicht erreichen, bevor sie zu einem Punkt kolllabiert.
Interessanter wird es für einen Beobachter, der von vorn herein in der Hohlkugel war. Anders als in einer homogenen Masseverteilung fällt er zunächst nicht ins Zentrum, sondern wird von der kollabierenden Hülle erschlagen bevor sich seine Überreste auf den Weg in die entstehende Singularität machen.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Aug 2021 13:26 Titel: index_razor Verfasst am: 10. Aug 2021 13:26 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | Wenn ein Stern unter den Radius seines Schwarzschildradius schrumpft, dann ist seine Ausdehnung im ersten Moment noch endlich. Dann ist seine Masse sagen wir m=1 und sein Schwarzschildradius Rs ebenfalls 1.
|
Der Schwarzschildradius ist r = 2M. Aber an der Logik ändert das natürlich nichts.
| Zitat: |
Wenn ich mir nun eine Kugel im Inneren vorstelle mit r=1/2, dann hat diese Kugel die Masse 1/8 (homogene Dichte vorausgesetzt). Der Schwarzschildradius dieser inneren Masse ist somit 1/8 und liegt somit weit unter 1/2. Ich würde mir naiv erwarten, dass die Gravitation abnimmt, wenn man weiter in das Innere vordringt, so wie ja bei der Newton'schen Gravitation nur das Innere der Umrandung zählt. Wahrscheinlich ist dies hier aber falsch...
Aber was wäre, wenn es sich im im Extremfall um eine Hohlkugel handelte? Dann müsste ja ihr Hohlraum feldfrei sein und der Raum dort "flach" ? Ein Teilchen würde dann ja auch nicht in den Hohlraum bis ins Zentrum fallen - oder etwa doch? Das ist meine "Überlegung" von oben auf die Spitze getrieben.
|
Das sind auch zwei verschiedene Fragen: 1) entsteht durch den Kollaps eine Singularität und 2) landet die gesamte kollabierende Materie innerhalb dieser Singularität. Die Antwort auf 1) lautet sicher "ja". 2) ist deutlich schwieriger zu beantworten, weil die Dynamik im Inneren der Sphäre während des gesamten Kollaps schwierig zu beschreiben ist. Mit Sicherheit landet die äußere Schicht in der Singularität. Das folgt zumindest für sphärische Verteilungen einfach aus der Form der äußeren Metrik und auch für geringe Abweichungen von der Sphärizität aus störungstheoretischen Rechnungen. Für die Materie im Inneren gilt das zwar vermutlich auch, aber zumindest zur Zeit als MTW geschrieben wurde, gab es dafür noch keinen Beweis, allerdings genügend Rechnungen, die zumindest darauf hindeuten, daß man hier keinerlei Überraschungen zu erwarten hat.
|
|
 |
|
|

















