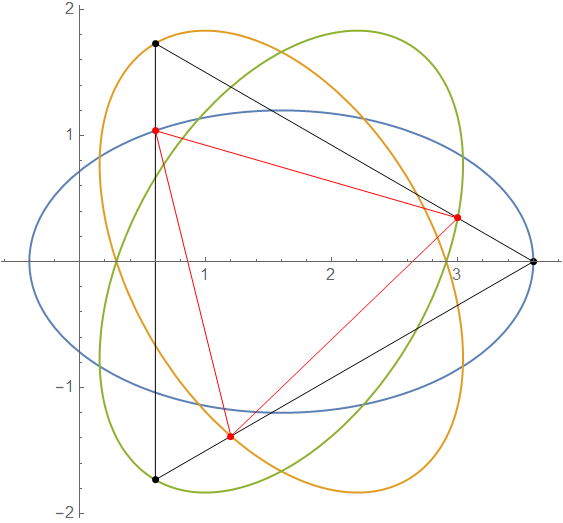
| Trajektorie (Dreikörperproblem mit gleichseitigem Dreieck) |
| Autor | Nachricht | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PhysikStudent(2.S) Gast |
||||||||||||||||||
| Huggy Anmeldungsdatum: 16.08.2012 Beiträge: 785 |
|
|||||||||||||||||
| PhysikStudent(2.S) Gast |
||||||||||||||||||
| Huggy Anmeldungsdatum: 16.08.2012 Beiträge: 785 |
|
|||||||||||||||||
| PhysikStudent(2.S) Gast |
|
|||||||||||||||||
| Momomarqui Gast |
|
|||||||||||||||||
| Verwandte Themen - die Neuesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Trägheitstensor Dreieck | 1 | rakete007 | 659 | 11. Jan 2024 19:41 Myon |
 |
Trajektorie berechnen relativistisches Teilchen in (1+1) Dim | 7 | Gast | 3059 | 07. Nov 2022 20:27 Understand_it |
 |
Trajektorie eines waagrechten Wurfes | 2 | stoky | 702 | 28. Jul 2021 23:29 Myon |
 |
Lichtbrechung im Dreieck | 1 | Gast | 791 | 03. Feb 2021 22:55 Myon |
 |
Trajektorie Ball | 3 | pharmacyl | 857 | 05. Mai 2020 14:15 pharmacyl |
| Verwandte Themen - die Größten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Induktion Dreieck | 29 | Tergo | 5239 | 25. Aug 2016 17:37 isi1 |
 |
Dreieck in Magnetfeld | 25 | Gast | 10629 | 20. Dez 2005 21:24 schnudl |
 |
Schwerpunkt y Koordinate Dreieck | 17 | Jussy | 3714 | 08. Jul 2012 14:52 Jussy |
 |
Schräger Wurf (Trajektorie maximal bei welchem Winkel) | 14 | Torxal | 2701 | 26. Apr 2016 10:28 Mathefix |
 |
Platte mit Loch und Dreieck | 12 | Armani42 | 1637 | 06. Nov 2014 00:09 jh8979 |
| Verwandte Themen - die Beliebtesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Kondensator Dreieck Stern Umwandlung | 7 | jenny93 | 13432 | 13. März 2013 21:38 D2 |
 |
Winkel im Dreieck berechnen / Dachneigung | 9 | kruemel680 | 12536 | 12. Dez 2016 14:52 Lisbet |
 |
Dreieck in Magnetfeld | 25 | Gast | 10629 | 20. Dez 2005 21:24 schnudl |
 |
stern dreieck umwandlung | 6 | Ascareth | 7552 | 17. Jan 2013 17:44 GvC |
 |
Ladungen in Quadrat und Dreieck: E-Kraft und E-Feld? | 5 | Sunny94 | 7535 | 10. Mai 2013 20:06 Sunny94 |