| Autor |
Nachricht |
Herr Fensterplatz
Anmeldungsdatum: 20.01.2021
Beiträge: 4
|
 Herr Fensterplatz Verfasst am: 20. Jan 2021 00:30 Titel: Aus Quaternionen/Beschleunigung Position bestimmen |
 |
|
Meine Frage:
Hallo,
Ich habe einen Xsens Sensor, den ich an einem Schläger (ein ähnliches Gerät wie beim Baseball) fixiert habe. Damit zeichne ich meine Schwünge auf. Leider ist die mitgeliferte App nicht wirklich der Hammer, daher würde ich gerne mit den exportierten Daten was machen. Das Ziel wäre, den Weg/die Position des Schlägers und die jeweilige Beschleunigung darstellen, um meine Präzision und die Abschlagsweite zu erhöhen.
Der Sensor liefert verschiedene Daten, aber für mein Vorhaben dürften wohl die Abtastrate (60Hz/120Hz), Quaternion und die Beschlenigung am interessantesten sein:
PacketCounter SampleTimeFine Quat_W Quat_X Quat_Y Quat_Z FreeAcc_X FreeAcc_Y FreeAcc_Z Status
1 683939112 0.615815 -0.000931 0.002483 -0.787888 -0.001394 0.006103 -0.071470 0
2 683955779 0.615845 -0.000860 0.002535 -0.787864 -0.002669 0.002893 -0.075724 0
3 683972446 0.615954 -0.000822 0.002561 -0.787779 0.005263 0.001928 -0.083133 0
4 683989113 0.615993 -0.000757 0.002546 -0.787749 -0.003528 0.003630 -0.087347 0
5 684005780 0.615970 -0.000714 0.002536 -0.787766 0.000861 -0.017395 -0.080033 0
6 684022447 0.615879 -0.000695 0.002483 -0.787838 -0.011306 0.007262 -0.090596 0
Wahrscheinlich ist das einfacher, wie gedacht, aber ich habe mir bezüglich der Quaternionen schon einiges durchgelesen und ich werde nicht so recht schlau draus, wie ich mit ihnen und der Beschleunigung die Position bestimmen kann?
Hat jemand eine Idee, wie sich das bewerkstelligen lässt?
Viele Grüsse,
Herr Fensterplatz
Meine Ideen:
Vermutung: Die Beschleunigung wird wahrscheinlich integriert werden müssen, um das ganze mittels Geschwindigkeit oder Weg zu lösen. Das würde dann wohl einen Vektor geben, der dann mit dem jeweiligen Q verrechnet werden muss.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 20. Jan 2021 12:10 Titel: Re: Aus Quaternionen/Beschleunigung Position bestimmen |
|
|
Hallo,
| Herr Fensterplatz hat Folgendes geschrieben: |
Vermutung: Die Beschleunigung wird wahrscheinlich integriert werden müssen, um das ganze mittels Geschwindigkeit oder Weg zu lösen.
|
Um von der Beschleunigung auf den Ort zu kommen, musst Du zweimal integrieren. Praxistauglich ist das m. E. nicht sonderlich.
Stell Dir vor, dass das Beschleunigungssignal einen kleinen Fehler von der Größe 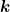 (für Konstante) hat. Beim einfachen Integrieren wird dieser Fehler zu  und beim doppelten Integrieren zu  . Der Fehler steigt also quadratisch mit der Zeit an.
Viele Grüße
Michael
|
|
|
B3N
Gast
|
| B3N Verfasst am: 20. Jan 2021 12:34 Titel: |
|
|
Hallo Michael,
danke für Deine rasche Antwort. Das stimmt natürlich, sehr genau wäre das evt. nicht. Aber wie würde man dann die Position des Schlägers (bzw. die Änderung) mit Hilfe der Quaternionen bestimmen? Machbar müsste es ja sein.
Sonst kann ich das mit mehreren Schlagversuchen mal durchrechnen, plotten und schauen, ob das einigermassen mit der Realität übereinstimmt?
Viele Grüsse,
Ben
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3400
|
| ML Verfasst am: 20. Jan 2021 13:57 Titel: |
|
|
| B3N hat Folgendes geschrieben: |
danke für Deine rasche Antwort. Das stimmt natürlich, sehr genau wäre das evt. nicht.
|
Ich habe so etwas vor etlichen Jahren im Rahmen einer studentischen Arbeit probiert. Die Ergebnisse aus einer solchen doppelten Integration sind nicht nur "nicht sehr genau", sondern sie sind absolut unbrauchbar.
Ich will nicht ausschließen, dass Du im Einzelfall was reißen kannst, wenn du einen guten Korrekturmechanismus (mit von den Beschleunigungssensoren unabhängigen Werten) hast. Wenn Du aber weitere, unabhängige Werte hast, ist die Frage, wozu Du die Beschleunigungswerte brauchst. Im Einzelfall -- wie gesagt -- gibt es da sicher sinnvolle Anwendungen, aber der allgemein Fall, der Dir vorschwebt, ist zum Scheitern verurteilt.
Wirklich nützlich sind die Beschleunigungswerte eigentlich nur für für die Erkennung eine zusätzlich wirkenden Kraft (Erkennung eines "Rucks", z. B. als Schrittzähler, zum Erkennen, ob Du mit dem Auto abbremst, scharf um die Kurve fährst o. ä.) und zur Bestimmung der Lage im Raum. Die 9,81 m/s² Erdbeschleunigung zeigen die Sensoren ja normalerweise an.
| Zitat: |
Aber wie würde man dann die Position des Schlägers (bzw. die Änderung) mit Hilfe der Quaternionen bestimmen? Machbar müsste es ja sein.
Sonst kann ich das mit mehreren Schlagversuchen mal durchrechnen, plotten und schauen, ob das einigermassen mit der Realität übereinstimmt?
|
Ich kenne Quaterionen als so eine Art komplexe Zahlen mit einem Realteil und drei Imaginärteilen i, j, k. Es gelten viele Rechenregeln, die wir im Komplexen kennen, weiter (die Körperaxiome gelten, die Multiplikation ist aber nicht kommutativ, z. B. ij = k, ji=-k); eine typische Anwendung sind Rotationen im R³.
Ich weiß aber weder, wie das in dem Sensor implementiert ist, noch erinnere ich mich im Detail, wie das mit den Drehungen funktionierte. Vielleicht kann jemand anderes helfen.
Hier ist vielleicht ein Anfang, der weiterhilft:
https://mathepedia.de/Quaternionen.html
Viele Grüße
Michael
|
|
|
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
| Steffen Bühler Verfasst am: 20. Jan 2021 14:34 Titel: |
|
|
Willkommen im Physikerboard!
Es wird hier wohl um eine spezielle Anwendung der Quaternionen gehen, die hier beschrieben ist. Aber auch die passt leider nicht hundertprozentig, denn dann wäre das W ein Rotationswinkel (genauer der Cosinus des halben Winkels), um den sich etwas um eine Achse, die durch X, Y und Z beschrieben ist, dreht. Aber es wird ja nicht alle 16ms eine solche Rotation durchgeführt, die durch das jeweilige Quaternion beschrieben ist.
Ich vermute daher, dass der Punkt (X|Y|Z) einfach die räumliche Position sein soll (wo sich also die Spitze des Schlägers gerade befindet), und W beschreibt die Verkippung des Schlägers. Z ändert sich bei den Daten eher wenig, X und Y dagegen zeigen eine Auf- und Ab-Bewegung, die tatsächlich eine (vielleicht durch den Winkel verzerrte) Schlägerbewegung darstellen könnte.
Aber vielleicht meldet sich der Experte im Python-Forum, wo die Anfrage zusätzlich gestellt wurde, ja noch einmal. Oder das Datenblatt des Sensors gibt noch etwas mehr her.
Viele Grüße
Steffen
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18079
|
| TomS Verfasst am: 20. Jan 2021 14:57 Titel: |
|
|
Siehe am besten hier:
https://en.m.wikipedia.org/wiki/Quaternions_and_spatial_rotation
Eine Rotation entspricht einer Transformation aus der Gruppe SO(3). Für die SO(3) gibt es verschiedene Darstellungen, die untereinander äquivalent sind.
Die bekannteste ist die Darstellung mittels Rotationsmatrizen R und Eulerwinkeln, d.h. Rotation um die Winkel alpha, beta, gamma jeweils um die Achsen z, x, z.
Ein wesentliche Problem ist, dass zu einer gegeben Rotation die Euler-Winkel schwierig zu bestimmen sind.
Die Darstellung mittels Quaternionen löst das Problem, wenn zu einer Rotation die Rotationsachse bzw. deren Einheitsvektor e und der Winkel theta bekannt sind.
Alles weitere wird mit Quaternionen nicht unbedingt einfacher.
Eine bijektive Umrechnung zwischen 3er-Vektoren und Quaternionen ist unproblematisch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Herr Fensterplatz
Anmeldungsdatum: 20.01.2021
Beiträge: 4
|
| Herr Fensterplatz Verfasst am: 20. Jan 2021 17:30 Titel: |
|
|
Hallo zusammen und vielen Dank für die Rückmeldungen und Tipps.
| Zitat: | | Aber vielleicht meldet sich der Experte im Python-Forum, wo die Anfrage zusätzlich gestellt wurde, ja noch einmal. |
Dessen Vorschlag war auch, es über die zweifache Integration der Beschleunigung zu machen. Nach Michaels Erfahrung scheint das aber ja zu ungenau zu sein.
| Zitat: | | Oder das Datenblatt des Sensors gibt noch etwas mehr her. |
Das Usermanual gibt die eine oder andere Info dazu:
4 Output Specifications
Data output from Xsens DOT is represented in different coordinate systems. Each data output is explained below.
4.1 Coordinate systems
4.1.1 Sensor coordinate system The sensor coordinate system (S) is a right-handed coordinate Cartesian system that is body-fixed to the sensor. Depicted below is the sensor coordinate system on DOT, using small x, y and z.
4.1.2 Orientation coordinate system By default, the local earth-fixed reference coordinate system (L) used is defined as a right-handed Cartesian coordinate system with:
• X positive to the East (E). • Y positive to the North (N). • Z positive when pointing up (U).
This coordinate system is known as ENU and is the standard in inertial navigation for aviation and geodetic applications. With the default ENU (L) coordinate system, Xsens yaw output is defined as the angle between East (X) and the horizontal projection of the sensor x-axis, positive about the local vertical axis (Z) following the right-hand rule. The origin of the reference frame is located in correspondence of the location of the accelerometer. For additional information on the position of the accelerometer, check out the Xsens DOT technical drawing at chapter 5.4.
The orientation calculated by Xsens DOT is the orientation of the sensor coordinate system (S) with respect to the local earth coordinate system (L). Xsens DOT can output a North referenced Yaw, also referred to as Heading. By default, the orientation output is in the
East-North-Up (ENU) frame, meaning that Roll, Pitch and Yaw will equal 0 degrees when the x-axis of the sensor is aligned with East, the y-axis with North and the z-axis upward:
• X positive when pointing to the local magnetic East • Y positive when pointing to the local magnetic North • Z positive when pointing up
oder hier das gesamte Manual:https://www.xsens.com/hubfs/Downloads/Manuals/Xsens%20DOT%20User%20Manual.pdf?hsCtaTracking=ba3917b0-c02b-4b83-9dd0-fcc0d06d0d13%7Ca200d741-4f23-4e67-9041-048d7a27de39
Ich habe mir die verlinkten Seiten angeschaut, konnte aber keine Rückschlüsse ziehen, welche von den Formeln denn nun für meinen Fall anzuwenden ist. Bzw. wenn Steffen recht hat, und w ein Kipp- statt eines Rotationswinkels ist, funktioniert es dann überhaupt mit den Quaternionrechenregeln?
| Zitat: | | Ich vermute daher, dass der Punkt (X|Y|Z) einfach die räumliche Position sein soll (wo sich also die Spitze des Schlägers gerade befindet), und W beschreibt die Verkippung des Schlägers. Z ändert sich bei den Daten eher wenig, X und Y dagegen zeigen eine Auf- und Ab-Bewegung, die tatsächlich eine (vielleicht durch den Winkel verzerrte) Schlägerbewegung darstellen könnte. |
Für die Daten habe ich den Sensor nur kurz geschüttelt, die bilden keine Schlagbewegung ab, ich habe da nur was schnelles generiert, damit man die Angaben sieht. Deine Beobachtung XY-Auf und Ab sollte also richtig sein.
Viele Grüsse
Ben
| Beschreibung: |
|
Download |
| Dateiname: |
Xsens coordinate system.pdf |
| Dateigröße: |
185.97 KB |
| Heruntergeladen: |
152 mal |
|
|
|
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
| Steffen Bühler Verfasst am: 20. Jan 2021 21:46 Titel: |
|
|
Ich hab mich jetzt mal ein bisschen durch die verschiedenenen pdfs gewühlt. Und glaube allmählich, dass meine Annahme stimmt. Die vier Quaternionwerte geben die Richtung einer Achse und aktuelle Verdrehung des Sensors an. Weitere Rechenregeln werden dafür nicht gebraucht.
Wo der Sensor auf dieser Achse aber tatsächlich ist, wird man wirklich nur über zweimaliges Aufaddieren der Beschleunigungswerte erreichen. Ich teile die Bedenken, dass ein kleiner konstanter Offset oder auch Rundungsfehler dadurch schnell zu einem Riesenwert kumulieren können. Ich habe mich früher mal einige Zeit damit beschäftigt, es gibt wohl Algorithmen, die das verhindern.
Aber probier es doch einfach erst mal so. Vielleicht kommt ja schon was Sinnvolles raus.
|
|
|
Herr Fensterplatz
Anmeldungsdatum: 20.01.2021
Beiträge: 4
|
| Herr Fensterplatz Verfasst am: 20. Jan 2021 23:44 Titel: |
|
|
Mit
| Zitat: | | nur über zweimaliges Aufaddieren der Beschleunigungswerte erreichen |
meinst du zweimaliges integrieren, oder? Nur um sicher zu gehen.
und wäre die zu verwendende Formel dann die hier für die Drehung?
"Position neu"=quaternion (w,x,y,z) * s (0,x,y,z) * konjugiertes quaternion (w,-x,-y,-z)
"s" entspricht dabei dem Vektor der aus der Integration der Beschleunigungswerte in x, y und z-Richtung kommt
Das ist dann auf alle Werte aus der Tabelle anzuwenden und die erhaltenen Daten für "Position neu" zu plotten?
|
|
|
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
| Steffen Bühler Verfasst am: 22. Jan 2021 14:57 Titel: |
|
|
Nein, die Quaternionen geben nur die Schlägerhaltung an! Mal ein ganz einfaches Beispiel:
Nimm einen Bleistift und halte ihn an einen Globus, die Spitze zum Nordpol. Der Berührpunkt wird nun durch die xyz-Parameter des Quaternions angegeben. Nun verdrehe den Bleistift, so dass die Spitze nicht mehr nach Norden zeigt. Dieser Drehwinkel (der Cosinus seiner Hälfte) wird durch w angegeben.
Damit ist die Schlägerhaltung im Raum eindeutig beschrieben. Aber wo sich der Schläger mit dieser Haltung nun im Raum befindet, ist etwas anderes! Dazu brauchst Du die Beschleunigungswerte. Die musst Du in der Tat zweimal integrieren. Das entspricht aber einem einfachen zweimaligem Aufaddieren, wie beim Zusammenzählen von Zahlen auf einer Rechnung. Sowas ist in Echtzeit schnell und genau genug. Auch hier ein einfaches Beispiel:
Nimm an, der Schläger hat zu Beginn Position Null und Geschwindigkeit Null. Und nun kommen im Sekundentakt diese Beschleunigungswerte: 1m/s^2, 2m/s^2, 3m/s^2, 4m/s^2. Wir betrachten nun nur die Tastzeitpunkte und nehmen Treppenfunktionen an, das ist nach Herrn Riemann erlaubt. Verfeinern kann man dann immer noch.
Wenn zum Zeitpunkt Null 1m/s^2 vorhanden sind, ist die Geschwindigkeit zum Zeitpunkt 1s natürlich 1m/s. Da wir nun bei Zeitpunkt 1s schon 2m/s^2 haben, wird die Geschwindigkeit bei 2s auf 3m/s gestiegen sein. Bei 3s dann 6m/s, dann 10m/s. Die Zahlen 1,2,3,4 werden also zur Reihe 1,3,6,10 aufaddiert. Und genauso kann man die dann zu den Positionen 1,4,10,20 aufaddieren.
Versuch das doch mal und berichte, ob was Sinnvolles rauskommt. Ich bin gespannt.
Viele Grüße
Steffen
|
|
|
Herr Fensterplatz
Anmeldungsdatum: 20.01.2021
Beiträge: 4
|
| Herr Fensterplatz Verfasst am: 23. Jan 2021 14:27 Titel: |
|
|
Hallo Steffen,
vielen Dank für die verständliche Ausführung.
Ich bin nun soweit, dass ich Test-Daten in Python einlesen und aus der Beschleunigung für x,y und z jeweils das v und s berechnen/plotten kann. Den Link zu den Quaternionen ist mir aber wohl immer noch nicht klar. Weil ich interpretiere deinen letzten Post so, dass der Ansatz hier
"Position neu"=quaternion * s * konjugiertes quaternion
nicht korrekt ist? Wie kommen die jetzt in die Gleichung rein? Weil brauchen tun wir sie ja, oder? Sorry, da bin ich leider immer noch verwirrt :-(
Viele Grüsse
Ben
|
|
|
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7244
|
| Steffen Bühler Verfasst am: 24. Jan 2021 12:27 Titel: |
|
|
Die Quaternion-Daten brauchst Du, damit Du die Weginformation in die richtige Richtung legst. Wenn Du beispielsweise herausgefunden hast, dass sich der Schläger nur in x-Richtung um 10 Zentimeter bewegt hat, dann ist das eben die aktuelle x-Richtung, die durch die parallel gelieferten xyz-Daten beschrieben wird. Die Verdrehung des Schlägers, also die w-Komponente, wird dafür nicht gebraucht.
Also ein bisschen Vektorrechnung. Ist nicht so mein Fachgebiet, eventuell passt die Konjugierten-Formel hier sogar.
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
