| Autor |
Nachricht |
du bist nicht ein
Gast
|
 du bist nicht ein Verfasst am: 25. Jun 2020 06:55 Titel: Quantenphysik und Zufall du bist nicht ein Verfasst am: 25. Jun 2020 06:55 Titel: Quantenphysik und Zufall |
 |
|
Ich habe dieses Video von Prof. Lesch über Zufall in der Physik gesehen und verstehe nicht wirklich, wie aus den Erklärungen Zufall folgt?
(auf Youtube nach Lesch und Zufall suchen, darf keinen Link als Unreg posten)
Einmal sagt er, dass Elektronen nicht in den Kern fallen, weil man nicht genau Ort und Implus (Masse * Geschwindigkeit) messen kann. Das Elektron fällt also nicht in den Kern, weil es immer schneller wird, je näher es am Kern ist, je genauer also seine Position bekannt ist. Das ist doch aber kein Zufall. Wenn es schneller ist, je genauer die Position bekannt ist, dann besteht da ein Zusammenhang zwischen Position und Geschwindigkeit. Zufall wäre es, wenn die Geschwindikeit, bei bekannter Position, auch ganz langsam sein könnte, dann würde aber das Elektron in den Kern fallen.
Habe ich seine Erklärung falsch verstanden? Hat er das falsch erklärt? Oder habt ihr in der Physik einfach definiert, dass alles, was ihr nicht genau messen könnt Zufall ist?
Auch die Erklärung am Ende, dass man im Großen keinen Zufall mehr hat, weil sich die Unbestimmtheit wegmittelt, hört sich nicht nach Zufall an.
Wenn man sehr viele Zahlen zwischen 0 und 10 zufällig auswählt, bekommt man im Mittel einen Durchschnitt von 5, aber man kommt nicht immer genau auf 5. Und bei echtem Zufall gibt es auch bei sehr vielen Zahlen eine ganz kleine Wahrscheinlichkeit, dass einmal der Durchschnitt 1 rauskommt. In der Welt der großen Dinge sieht man aber nicht, dass Dinge sich immer so leicht zufällig verhalten (man kommt nicht immer genau auf 5) und man sieht auch nie, dass ein Ding, dass 5 cm groß ist mal für einen ganz kurzen Zeitraum zufällig 1 cm groß ist (eine ganz kleine Wahrscheinlichkeit, dass einmal der Durchschnitt 1 rauskommt). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18001
|
 TomS Verfasst am: 25. Jun 2020 08:48 Titel: TomS Verfasst am: 25. Jun 2020 08:48 Titel: |
 |
|
Vorab: ich bin kein Fan der Erklärungen von Prof. Lesch. Einiges, was ich gesehen habe, ist so verzerrt oder verschwommen dargestellt, dass es nur wenig mit dem zu tun hat, was tatsächlich Sache ist. Daneben erfüllt es offenbar seinen eigentlichen Zweck nicht, nämlich eine verständliche und dennoch einigermaßen zutreffende Erklärung zu liefern; andernfalls dürfte es ja keine derartige Verwirrung geben. Und zuletzt bin ich der Meinung, dass man es besser machen könnte, allerdings evtl. nicht in diesem Format.
Dann zur Quantenmechanik: diese ist im mathematischen Kern nicht zufällig! Allerdings benötigt man zur physikalischen Interpretation dieses mathematischen Kerns teilweise den Begriff der Wahrscheinlichkeiten, die sich jedoch für eine Vielzahl von physikalischen Systemen und Vorgängen präzise berechnen lassen.
Mittels der Quantenmechanik und der Erweiterungen wie insbesondere der Quantenfeldtheorien können wir heute diverse messbare Eigenschaften sehr genau berechnen: Spektren von Atomen, Streuquerschnitte, Eigenschaften von Festkörpern wie z.B. Supraleitung, Massen von Protononen, Neutronen, ...
Was wir jedoch nicht gesichert sagen können ist, was ein System tut, wenn wir es nicht beobachten. Zwar haben wir dafür exakte Gleichungen ohne jeden Zufall und können diese oft in sehr guter Näherung lösen, jedoch können wir das Ergebnis nicht experimentell prüfen, da wir es damit beobachten und stören würden. Kurz: wir können nicht durch Beobachtung prüfen, wie sich ein unbeobachtetes System verhält. Viele Physiker haben sich demnach davon verabschiedet, dass uns die Quantenmechanik eine Antwort auf die Frage liefert, wie sich die Natur tatsächlich verhält, wenn wir sie nicht beobachten, sie beschränken sich auf die Berechnung messbarer Größen.
Zum Beispiel des Elektrons, das nicht in den Kern stürzt: das Elektron wird in der Quantenmechanik nicht als punktförmiges Objekt beschrieben, sondern mittels einer sogenannten Wellenfunktion. Mittels dieser kann man eine Wahrscheinlichkeit berechnen, wo sich das Elektron aufhält. Es gibt dazu letztlich zwei zentrale Gleichungen, die deterministische Schrödingergleichung, sowie eine zur Berechnung dieser Wahrscheinlichkeit.
(welche Kenntnisse in Mathematik hast du?)
Die Dynamik der Wellenfunktion psi mittels Schrödingergleichung tritt an die Stelle der Newtonschen Bewegungsgleichungen. Sie lautet
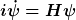
Der Punkt steht für die Zeitableitung, H für den sogenannten Hamiltonoperator (du musst nicht die Details verstehen, es geht lediglich darum, dass klar wird, dass hier kein Zufall ins Spiel kommt).
Die Berechnung der Wahrscheinlichkeit p[B], dass sich das Elektron in einem bestimmten Raumbereich B befindet, funktioniert ebenfalls mittels dieser Wellenfunktion
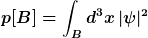
Löst man die Schrödingergleichung für das Elektron im Wasserstoffatom und berechnet die Aufenthaltswahrscheinlichkeit für das Elektron im Kern, so folgt

D.h. zum einen, dass sich das Elektron tatsächlich im Kern aufhält, dass es sich jedoch auch außerhalb des Kerns aufhält - das ist sogar deutlich wahrscheinlicher - und dass die Aufenthaltswahrscheinlichkeit zeitlich konstant ist.
Würde das Elektron „in den Kern stürzen“, dann würde man erwarten, dass
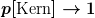
- innerhalb eines sehr kurzen Zeitraums.
Das ist offenbar nicht der Fall.
Auch ein Maß für die Größe des Atoms kann man präzise berechnen. Man nutzt dazu den Erwartungswert für den Radius. Dieser berechnet sich zu
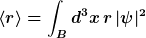
Auch hier gilt
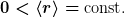
Würde das Elektron „in den Kern stürzen“, dann würde man erwarten, dass
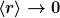
Auch das ist nicht der Fall.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
du bist nicht ein
Gast
|
 du bist nicht ein Verfasst am: 29. Jun 2020 06:27 Titel: du bist nicht ein Verfasst am: 29. Jun 2020 06:27 Titel: |
 |
|
|
Könnte man dann eigentlich in einem (kleinen) theoretischen Universum, in dem alle Zustände bekannt sind und man nichts messen muss, jeden Vorgang deterministisch berechnen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18001
|
 TomS Verfasst am: 29. Jun 2020 07:33 Titel: TomS Verfasst am: 29. Jun 2020 07:33 Titel: |
 |
|
Sicher, die o.g. Schrödingergleichung
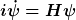
leistet genau dies.
Wenn der Zustand bzw. die Wellenfunktion psi bekannt sind, dann entwickeln sich diese streng deterministisch und können prinzipiell beliebig genau sowie für beliebige Zeiten in der Zukunft berechnet werden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5038
|
 DrStupid Verfasst am: 29. Jun 2020 08:51 Titel: DrStupid Verfasst am: 29. Jun 2020 08:51 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | D.h. zum einen, dass sich das Elektron tatsächlich im Kern aufhält, dass es sich jedoch auch außerhalb des Kerns aufhält - das ist sogar deutlich wahrscheinlicher - und dass die Aufenthaltswahrscheinlichkeit zeitlich konstant ist. |
Das könnte auch ein falsches Bild vermitteln. Die Wahrscheinlichkeit, auf ein 1s-Elektron zu treffen wird umso größer, je näher man dem Kern kommt und im Kern wird seine Aufenthaltswahrscheinlichkeitsdichte maximal. Dass solche Elektronen trotzdem mit größerer Wahrscheinlichkeit außerhalb des Kerns zu finden sind, liegt daran, dass der Kern im Vergleich zum gesamten Atom sehr klein ist.
| TomS hat Folgendes geschrieben: | Würde das Elektron „in den Kern stürzen“, dann würde man erwarten, dass
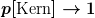
- innerhalb eines sehr kurzen Zeitraums. |
Das würde man erwarten, wenn das Elektron nach dem Sturz in den Kern auch dort bleiben würde. Das tut es aber nicht.
Rest gelöscht, da im weiteren irrelevante Diskussionen; TomS |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18001
|
 TomS Verfasst am: 29. Jun 2020 12:29 Titel: TomS Verfasst am: 29. Jun 2020 12:29 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | D.h. zum einen, dass sich das Elektron tatsächlich im Kern aufhält, dass es sich jedoch auch außerhalb des Kerns aufhält - das ist sogar deutlich wahrscheinlicher - und dass die Aufenthaltswahrscheinlichkeit zeitlich konstant ist. |
Das könnte auch ein falsches Bild vermitteln. Die Wahrscheinlichkeit, auf ein 1s-Elektron zu treffen wird umso größer, je näher man dem Kern kommt und im Kern wird seine Aufenthaltswahrscheinlichkeitsdichte maximal. Dass solche Elektronen trotzdem mit größerer Wahrscheinlichkeit außerhalb des Kerns zu finden sind, liegt daran, dass der Kern im Vergleich zum gesamten Atom sehr klein ist. |
Stimmt.
Die Wahrscheinlichkeit für ein Elektron innerhalb einer Kugelschale bei Radius r und Dicke dr folgt z.B. für den Grundzustand mittels
|^2 = 4\pi \, r^2 \, |\psi_{100}(r)|^2 \, dr)
und dieser Integrand hat ein Maximum bei
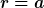
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Würde das Elektron „in den Kern stürzen“, dann würde man erwarten, dass
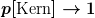
- innerhalb eines sehr kurzen Zeitraums. |
Das würde man erwarten, wenn das Elektron nach dem Sturz in den Kern auch dort bleiben würde. Das tut es aber nicht. |
Richtig, das tut es nicht.
Nach Modellen der klassischen Physik unter Einbeziehung des Elektromagnetismus würde man jedoch genau das erwarten.
gelöscht, da unnötig; TomS
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 29. Jun 2020 18:09, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18001
|
 TomS Verfasst am: 29. Jun 2020 18:00 Titel: TomS Verfasst am: 29. Jun 2020 18:00 Titel: |
 |
|
Ich habe aufgeräumt und die nicht zielführende Diskussion gelöscht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















