| Autor |
Nachricht |
nostalgia
Anmeldungsdatum: 10.04.2020
Beiträge: 1
|
 nostalgia Verfasst am: 10. Apr 2020 02:17 Titel: Schräger Wurf: Abweichung Winkel, v nostalgia Verfasst am: 10. Apr 2020 02:17 Titel: Schräger Wurf: Abweichung Winkel, v |
 |
|
Meine Frage:
Ein Ball (Durchmesser 10cm) soll durch einen Ring (Koordinaten x=1.5m und y=3m des Ringmittelpunkts, Ringdurchmesser: 40cm) in ein Zielfeld (Koordinaten x=5m und y=0m des Zielfeldmittelpunkts) geworfen werden. Der Ball wird im Abwurfpunkt (Koordinaten x=0 und y=2m) mit dem Abwurfwinkel a und der Abwurfgeschwindigkeit v0 abgeworfen. Die Reibung kann hier vernachlässigt werden.
b) Die Zielfeldmitte soll getroffen werden: Berechne die maximale Variation des Abwurfwinkels a und der Abwurfgeschwindigkeit v0 (absolut und prozentual), damit der Ball noch durch den Ring fliegt. Ich weiß leider nicht Mal wirklich, wo ich anfangen soll, um dies zu lösen.
In a) war v0= 5,92m/s und a=45° gegeben. Es soll berechnet werden, ob der Ball durch den Ring fliegt und ob die Zielfeld Mitte getroffen wird. Das habe ich bereits gelöst. Ich weiß aber nicht ob diese Infos für b) benötigt werden. Außerdem bin ich mir nicht Mal sicher ob ich die Aufgabe richtig verstehe: Die Abweichung von was denn??
Ich hoffe, da kann jemand helfen, bin leider wirklich etwas verzweifelt, weil ich einfach keine Lösung finde.
Meine Ideen:
Eventuell muss man hier mit Hilfe der Bahnkurve y(x) irgendwie verschiedene Winkel bzw. Anfangsgeschwindigkeiten einsetzen. Allerdings weiß ich nicht ganz, wie genau das funktionieren soll, da ich ja mit dem Winkel und der Geschwindigkeit immer zwei Unbekannte habe.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 10:59 Titel: Mathefix Verfasst am: 10. Apr 2020 10:59 Titel: |
 |
|
zu b)
d = Durchmesser des Balls
D = Durchmesser des Rings
x_D = Abstand Ring von Abwurfstelle
x_Z = Abstand Ziel von der Abwurfstelle
y_D = Höhe Mittelpunkt Ring
h = Höhe des Balls
Beta = Winkel der Bahnkurve gegenüber der x-Achse
Damit der Ball gerade noch durch den Ring fliegt, darf die Höhe seines Mittelpunkts an der Stelle x = x_D
a) An der Unterkante des Rings
 )
b) An der Oberkante des Rings
 )
betragen.
 << y_D \pm\frac{D}{2}: \beta_{u/o} = 0\rightarrow \cos( \beta_{u/o}) = 1)

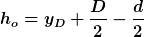
Bewegungsgleichungen
Für die Ober- und Unterkante des Rings: Je 2 Gleichungen mit den Unbekannten v_0 und Alpha.
Höhen werden erreicht:
 - \frac{g}{2}\cdot \frac{x_D^{2} }{v_0^{2}\cdot \cos^{2} (\alpha ) } )
 - \frac{g}{2}\cdot \frac{x_D^{2} }{v_0^{2}\cdot \cos^{2} (\alpha ) } )
Ziel wird erreicht:
 } = \frac{v_0\cdot \sin(\alpha ) }{g}+ \sqrt{\frac{2\cdot h_0}{g} + (\frac{v_0\cdot \sin(\alpha ) }{g} )^{2} } \Rightarrow v_0 )
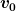 einsetzen in einsetzen in 
Existiert überhaupt eine analytische Lösung?
Zuletzt bearbeitet von Mathefix am 10. Apr 2020 18:15, insgesamt 21-mal bearbeitet |
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 10. Apr 2020 11:08 Titel: blödi123 Verfasst am: 10. Apr 2020 11:08 Titel: |
 |
|
für Abwurfwinkel 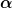 und Anfangsgeschwindigkeit und Anfangsgeschwindigkeit  erhalte ich folgende Bedingungen: erhalte ich folgende Bedingungen:
 \geq \sqrt{6 \cdot g} )
sowie
 - \frac{0,75 \cdot g}{{v_0}^2 \cdot {cos(\alpha)}^2} \leq 0,76 )
ohne Einheiten, da alles im SI-System, nun gilt es, diese beiden Bedingungen zu verarbeiten...
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 11:18 Titel: Mathefix Verfasst am: 10. Apr 2020 11:18 Titel: |
 |
|
| blödi123 hat Folgendes geschrieben: | für Abwurfwinkel 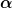 und Anfangsgeschwindigkeit und Anfangsgeschwindigkeit  erhalte ich folgende Bedingungen: erhalte ich folgende Bedingungen:
 \geq \sqrt{6 \cdot g} )
sowie
 - \frac{0,75 \cdot g}{{v_0}^2 \cdot {cos(\alpha)}^2} \leq 0,76 )
ohne Einheiten, da alles im SI-System, nun gilt es, diese beiden Bedingungen zu verarbeiten... |
Das kann von den Einheiten her nicht stimmen.
|
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 10. Apr 2020 12:04 Titel: blödi123 Verfasst am: 10. Apr 2020 12:04 Titel: |
 |
|
|
Moment mal bitte, muss (später) überprüfen...
|
|
 |
innovationonanostalgiatri
Anmeldungsdatum: 16.02.2020
Beiträge: 19
|
 innovationonanostalgiatri Verfasst am: 10. Apr 2020 15:10 Titel: innovationonanostalgiatri Verfasst am: 10. Apr 2020 15:10 Titel: |
 |
|
|
Trotzdem schon mal vielen vielen Dank für die Hilfe. Leider verstehe ich nicht ganz warum bei hu und ho noch mal mit dem Kosinus multipliziert wird. Wieso ist die Höhe, die der Mittelpunkt des Balls erreichen darf abhängig vom Abwurfwinkel?
|
|
 |
innovationonanostalgiatri
Anmeldungsdatum: 16.02.2020
Beiträge: 19
|
 innovationonanostalgiatri Verfasst am: 10. Apr 2020 15:15 Titel: innovationonanostalgiatri Verfasst am: 10. Apr 2020 15:15 Titel: |
 |
|
|
Ich gehe mal davon aus, dass aus den Bedingungen dann ein Gleichungssystem mit 3 Gleichungen erstellt werden muss. Allerdings weiß ich nicht, wie ich dieses dann lösen soll, habe nur einen normalen WTR von Casio, der kann das leider nicht. Vielleicht fehlen mir hier auch einfach ein paar elementare mathematische Fähigkeiten. Gibt es da irgendeinen "Trick" um so etwas zu lösen?
|
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 10. Apr 2020 16:38 Titel: blödi123 Verfasst am: 10. Apr 2020 16:38 Titel: |
 |
|
Mthefix: "Das kann von den Einheiten her nicht stimmen."
Selbstverständlich stimmt das (beachte meine Bemerkung "..SI-System..)
die beanstandete Ungleichung lautet ausführlich geschrieben:
 - \frac{1,125 m^2 \cdot g}{{(v_o \cdot cos(\alpha))}^2} \leq 1,15 m )
Ungleichungen durch 1,5 m dividieren:
 - \frac{0,75 m \cdot g}{{(v_o \cdot cos(\alpha))}^2} \leq 0,76 )
...und man sieht sofort, dass einheitenmäßig alles ok ist. Klar ist: es ist besser, korrekt zu notieren...
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 17:03 Titel: Mathefix Verfasst am: 10. Apr 2020 17:03 Titel: |
 |
|
| innovationonanostalgiatri hat Folgendes geschrieben: | | Trotzdem schon mal vielen vielen Dank für die Hilfe. Leider verstehe ich nicht ganz warum bei hu und ho noch mal mit dem Kosinus multipliziert wird. Wieso ist die Höhe, die der Mittelpunkt des Balls erreichen darf abhängig vom Abwurfwinkel? |
1. Da die Bahnkurve an der Stelle x= x_D einen Steigungswinkel Beta hat, tangiert der Ball den Ring nicht waagerecht, sondern unter diesem Steigungswinkel. Das hat zur Folge, dass sich der Mittelpunkt des Balls verschiebt. Da diese Verschiebung sehr klein ist, kann sie vernachlässigt werden: Vereinfacht die Rechnung erheblich.
2. Der Winkel Beta ist nicht der Abwurfwinkel, sondern der Winkel der Bahnkurve an der Stelle x = x_D.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 17:05 Titel: Mathefix Verfasst am: 10. Apr 2020 17:05 Titel: |
 |
|
| blödi123 hat Folgendes geschrieben: | Mthefix: "Das kann von den Einheiten her nicht stimmen."
Selbstverständlich stimmt das (beachte meine Bemerkung "..SI-System..)
die beanstandete Ungleichung lautet ausführlich geschrieben:
 - \frac{1,125 m^2 \cdot g}{{(v_o \cdot cos(\alpha))}^2} \leq 1,15 m )
Ungleichungen durch 1,5 m dividieren:
 - \frac{0,75 m \cdot g}{{(v_o \cdot cos(\alpha))}^2} \leq 0,76 )
...und man sieht sofort, dass einheitenmäßig alles ok ist. Klar ist: es ist besser, korrekt zu notieren... |
Danke, alles klar. Da Du schon das Ergebnis hast, wäre es hilfreich, wenn Du auch die Herleitung zeigen würdest.
|
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 10. Apr 2020 17:17 Titel: blödi123 Verfasst am: 10. Apr 2020 17:17 Titel: |
 |
|
nein, nein: ich habe noch kein End(!)ergebnis, ich bin vielmehr noch am Tüfteln - leider bin ich immer mal zeitlich verhindert.
Bis jetzt muss ich sagen: diese Aufgabe hat es etwas in sich...
Der Weg ist eigentlich klar: die Wurfweite bestimmt die Flugdauer T:
y(T)=0 - das ergibt einen weiteren Zusammenhang zwischen alpha und v_0.
Leider bläht sich das formal stark auf.
|
|
 |
innovationonanostalgiatri
Anmeldungsdatum: 16.02.2020
Beiträge: 19
|
 innovationonanostalgiatri Verfasst am: 10. Apr 2020 17:36 Titel: innovationonanostalgiatri Verfasst am: 10. Apr 2020 17:36 Titel: |
 |
|
|
Vielen Dank das hat zumindest schon mal weiter geholfen. Die Aufgabe ist leider wirklich sehr schwer.
|
|
 |
innovationonanostalgiatri
Anmeldungsdatum: 16.02.2020
Beiträge: 19
|
 innovationonanostalgiatri Verfasst am: 10. Apr 2020 18:04 Titel: innovationonanostalgiatri Verfasst am: 10. Apr 2020 18:04 Titel: |
 |
|
|
Inwiefern bestimmt die Wurfweite die Flugdauer? In den Formeln, die ich dazu habe, kann ich keinen Zusammenhang erkennen. Gibt es eine Formel die denn Zusammenhang beschreibt?
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 18:05 Titel: Mathefix Verfasst am: 10. Apr 2020 18:05 Titel: |
 |
|
| blödi123 hat Folgendes geschrieben: | nein, nein: ich habe noch kein End(!)ergebnis, ich bin vielmehr noch am Tüfteln - leider bin ich immer mal zeitlich verhindert.
Bis jetzt muss ich sagen: diese Aufgabe hat es etwas in sich...
Der Weg ist eigentlich klar: die Wurfweite bestimmt die Flugdauer T:
y(T)=0 - das ergibt einen weiteren Zusammenhang zwischen alpha und v_0.
Leider bläht sich das formal stark auf. |
Ich vermute, dass keine analytische Lösung existiert.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 18:06 Titel: Mathefix Verfasst am: 10. Apr 2020 18:06 Titel: |
 |
|
| innovationonanostalgiatri hat Folgendes geschrieben: | | Inwiefern bestimmt die Wurfweite die Flugdauer? In den Formeln, die ich dazu habe, kann ich keinen Zusammenhang erkennen. Gibt es eine Formel die denn Zusammenhang beschreibt? |
Die Wurfdauer T_Z wird durch die Steigzeit t_s und Fallzeit t_f bestimmt. Sie ist gleich der Zeit bis zum Ziel.
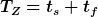
 } = \frac{v_0\cdot \sin(\alpha ) }{g}+ \sqrt{\frac{2\cdot h_0}{g} + (\frac{v_0\cdot \sin(\alpha ) }{g} )^{2} } )
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 18:28 Titel: Mathefix Verfasst am: 10. Apr 2020 18:28 Titel: |
 |
|
| innovationonanostalgiatri hat Folgendes geschrieben: | | Vielen Dank das hat zumindest schon mal weiter geholfen. Die Aufgabe ist leider wirklich sehr schwer. |
Vermutlich analytisch nicht lösbar.
Wer hat die Aufgabe gestellt? Gibt es eine Musterlösung?
|
|
 |
innovationonanostalgiatri
Anmeldungsdatum: 16.02.2020
Beiträge: 19
|
 innovationonanostalgiatri Verfasst am: 10. Apr 2020 18:52 Titel: innovationonanostalgiatri Verfasst am: 10. Apr 2020 18:52 Titel: |
 |
|
|
Ich studiere im 1. Semester Physik und diese Aufgabe ist Teil der Pflicht-Übungsaufgaben zu den ersten beiden Vorlesungen. Deswegen kann das doch eigentlich nicht so schwer sein, oder? Für Leute, die gerade mal knapp zwei Wochen studieren, muss das doch lösbar sein. Eine Musterlösung bekomme ich erst, wenn ich meine Lösungen abgegeben habe.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Apr 2020 19:28 Titel: Mathefix Verfasst am: 10. Apr 2020 19:28 Titel: |
 |
|
| innovationonanostalgiatri hat Folgendes geschrieben: | | Ich studiere im 1. Semester Physik und diese Aufgabe ist Teil der Pflicht-Übungsaufgaben zu den ersten beiden Vorlesungen. Deswegen kann das doch eigentlich nicht so schwer sein, oder? Für Leute, die gerade mal knapp zwei Wochen studieren, muss das doch lösbar sein. Eine Musterlösung bekomme ich erst, wenn ich meine Lösungen abgegeben habe. |
ich versuche es morgen mit EES , geht einfacher glaube ich.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 11. Apr 2020 13:47 Titel: Mathefix Verfasst am: 11. Apr 2020 13:47 Titel: |
 |
|
zu b)
d = Durchmesser des Balls
D = Durchmesser des Rings
x_D = Abstand Ring von Abwurfstelle
x_Z = Abstand Ziel von der Abwurfstelle
y_D = Höhe Mittelpunkt Ring
h = Höhe des Ballschwerpunkts
Beta = Winkel der Bahnkurve gegenüber der x-Achse
Damit der Ball gerade noch durch den Ring fliegt, darf die Höhe seines Mittelpunkts an der Stelle x = x_D
a) An der Unterkante des Rings
 )
b) An der Oberkante des Rings
 )
betragen.
 << y_D \pm\frac{D}{2}: \beta_{u/o} = 0\rightarrow \cos( \beta_{u/o}) = 1)


EES:
 )
 }\cdot \sqrt{2\cdot g\cdot (h_U -h_0)} )
Bewegungsgleichung
\cdot t)
 \cdot t-\frac{1}{2} \cdot g\cdot t^{2} = 0)
 }{g} + \sqrt{\frac{v_0^{2} \cdot \sin^{2} (\alpha ) }{g^{2} }+ \frac{2\cdot h_0}{g} } )
\cdot (\frac{v_0\cdot \sin(\alpha ) }{g} + \sqrt{\frac{v_0^{2} \cdot \sin^{2} (\alpha ) }{g^{2} }+ \frac{2\cdot h_0}{g} }) )
 }\cdot \sqrt{2\cdot g\cdot (h_U-h_0)}\cdot (\frac{1}{g} + \sqrt{\frac{2\cdot (h_U-h_0)}{g^{2} }+ \frac{2\cdot h_0}{g} }) )
 = \frac{ \sqrt{2\cdot g\cdot (h_U -h_0)}}{x_Z }\cdot (\frac{1}{g} + \sqrt{\frac{2\cdot (h_U-h_0)}{g^{2} }+ \frac{2\cdot h_0}{g} }) )
Winkel und Geschwindigkeit
}}{x_Z }\cdot (\frac{1}{g} + \sqrt{\frac{2\cdot (h_U-h_0)}{g^{2} }+ \frac{2\cdot h_0}{g} }) ))
 }\cdot \sqrt{2\cdot g\cdot (h_U -h_0)} )
Falls ich mich nicht verechnet habe.
Rechnung für h_O sinngemäß.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 11. Apr 2020 18:24 Titel: Myon Verfasst am: 11. Apr 2020 18:24 Titel: |
 |
|
@Mathefix: Zumindest eine der Grössen (Winkel und Geschwindigkeit) müsste auch von x_D abhängig sein, wahrscheinlich beide. Ausserdem sehe ich das Problem, dass grundsätzlich auch 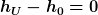 sein kann. Die Geschwindigkeit sollte deshalb aber nicht verschwinden. sein kann. Die Geschwindigkeit sollte deshalb aber nicht verschwinden.
Um das Ganze etwas systematisch zu machen: So wie ich es sehe, geht es darum, für 2 Fälle die Grössen ) einer Wurfparabel zu bestimmen, die jeweils durch 3 Punkte (x1,y1), (x2,y2), (x3,y3) geht. Man hat also 3 Gleichungen einer Wurfparabel zu bestimmen, die jeweils durch 3 Punkte (x1,y1), (x2,y2), (x3,y3) geht. Man hat also 3 Gleichungen

c=h0 ist unmittelbar klar. a und b kann man durch Auflösen des Systems bestimmen, und mit a, b, c ergeben sich auch alpha und v0.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 11. Apr 2020 18:37 Titel: Mathefix Verfasst am: 11. Apr 2020 18:37 Titel: |
 |
|
| Myon hat Folgendes geschrieben: |
Um das Ganze etwas systematisch zu machen: So wie ich es sehe, geht es darum, für 2 Fälle die Grössen ) einer Wurfparabel zu bestimmen, die jeweils durch 3 Punkte (x1,y1), (x2,y2), (x3,y3) geht. Man hat also 3 Gleichungen einer Wurfparabel zu bestimmen, die jeweils durch 3 Punkte (x1,y1), (x2,y2), (x3,y3) geht. Man hat also 3 Gleichungen

c=h0 ist unmittelbar klar. a und b kann man durch Auflösen des Systems bestimmen, und mit a, b, c ergeben sich auch alpha und v0. |
@Myon
vielen Dank für Deinen Kommentar. Den Gedanken hatte ich auch, hatte ihn aber zugunsten einer physikalischen Lösung nicht weiter verfolgt.
Du hast recht, führt schnell zur Lösung.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 12. Apr 2020 12:22 Titel: Mathefix Verfasst am: 12. Apr 2020 12:22 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | @Mathefix: Zumindest eine der Grössen (Winkel und Geschwindigkeit) müsste auch von x_D abhängig sein, wahrscheinlich beide. Ausserdem sehe ich das Problem, dass grundsätzlich auch 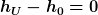 sein kann. Die Geschwindigkeit sollte deshalb aber nicht verschwinden. sein kann. Die Geschwindigkeit sollte deshalb aber nicht verschwinden.
Um das Ganze etwas systematisch zu machen: So wie ich es sehe, geht es darum, für 2 Fälle die Grössen ) einer Wurfparabel zu bestimmen, die jeweils durch 3 Punkte (x1,y1), (x2,y2), (x3,y3) geht. Man hat also 3 Gleichungen einer Wurfparabel zu bestimmen, die jeweils durch 3 Punkte (x1,y1), (x2,y2), (x3,y3) geht. Man hat also 3 Gleichungen

c=h0 ist unmittelbar klar. a und b kann man durch Auflösen des Systems bestimmen, und mit a, b, c ergeben sich auch alpha und v0. |
Unter der Voraussetzung, dass ich mich nicht verrechnet habe:


= 2\cdot a\cdot x + b)
_{x = 0} = b = 0,754)

Vllt. kann jemand v_o bestimmen.
PS
Ooops, doch verrechnet! Wenn ich Zeit habe korrigiere ich.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 13. Apr 2020 11:34 Titel: Mathefix Verfasst am: 13. Apr 2020 11:34 Titel: |
 |
|
Richtiges Ergebnis



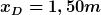
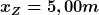
Winkel
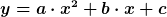
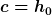

_{x = 0} = b )
}{x_D\cdot x_Z^{2}- x_Z\cdot x_D^{2} } )
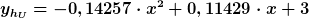



Geschwindigkeit
(1)  - \frac{g}{2}\cdot (\frac{x_D }{v_{0_{U/O}}\cdot \cos(\alpha_{U/O} ) }) ^{2} )
(2)  - \frac{g}{2}\cdot (\frac{x_Z }{v_{0_{U/O}}\cdot \cos(\alpha_{U/O} ) }) ^{2})
(1) - (2) = (3)
(3)  }{2\cdot (h_{_{U/O}}+\tan(\alpha_{U/O} )\cdot (x_Z-x_D) )\cdot \cos^{2}(\alpha_{U/O}) } }
<br />
)
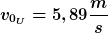
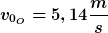
Ergebnisse durch Kontrollrechnung verifiziert.
Zuletzt bearbeitet von Mathefix am 13. Apr 2020 19:46, insgesamt 7-mal bearbeitet |
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 13. Apr 2020 12:04 Titel: blödi123 Verfasst am: 13. Apr 2020 12:04 Titel: |
 |
|
@Mathefix: "richtiges Ergebnis..." ich erhalte etwas ganz anderes (überlege mal deine Abwurfwinkel!)
Mit den erläuterten Einschränkungen von Mathefix (was die Art des Durchflugs durch den Ring angeht) den Hinweisen von Myon (die die ganze Rechnerei wesentlich vereinfachen) und mit den angegebenen Werten erhalte ich:
"o" - oberer Grenzfall, "u" - unterer Grenzfall


insgesamt:


|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 13. Apr 2020 12:50 Titel: Mathefix Verfasst am: 13. Apr 2020 12:50 Titel: |
 |
|
| blödi123 hat Folgendes geschrieben: | @Mathefix: "richtiges Ergebnis..." ich erhalte etwas ganz anderes (überlege mal deine Abwurfwinkel!)
Mit den erläuterten Einschränkungen von Mathefix (was die Art des Durchflugs durch den Ring angeht) den Hinweisen von Myon (die die ganze Rechnerei wesentlich vereinfachen) und mit den angegebenen Werten erhalte ich:
"o" - oberer Grenzfall, "u" - unterer Grenzfall


insgesamt:

 |
1. Wenn man in meine Gleichung y = ... die Zahlenwerte einsetzt, ergibt sich, dass die Funktion an den Stellen x= 0, y = h_0; x=x_D, y = h_u/O; x=x_Z , y = 0 erfüllt ist.
D.h. die Funktion ist korrekt.
2. An der Stelle x=0 ist der Koeffizient b die Steigung der Funktion d. h. der Tangens des Abwurfwinkels.
Aus 1. und 2. folgt, dass die Abwurfwinkel korrekt sind.
Überprüfe, ob Deine Werte diese Bedingungen erfüllen.
Für eher geringe Winkel spricht, dass Ober- und Unterkante des Rings nahe bei h_0 liegen und der Abstand des Rings vom Abwurfpunkt gering ist.
PS
Da Du nur Endergebnisse zeigst, kann man Deinen Ansatz und Lösungsweg nicht nachvollziehen.
|
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 13. Apr 2020 20:01 Titel: blödi123 Verfasst am: 13. Apr 2020 20:01 Titel: |
 |
|
@Mathefix - betrachte doch nur mal - ganz ohne Physik - das Dreieck mit den Punkten (0/2), (1,5/2), (1,5/2, - Abwurfpunkt/untere Ringkante - Abwurfpunkt/untere Ringkante
da ist tan alpha = 0,8/1,5 und damit alpha=28° - beim schiefen Wurf ist der Abwurfwinkel bestimmt größer als 28°, jedenfalls kommt als untere Grenze keinesfalls 6,5° in Frage.
Den von Myon vorgeschlagenen Weg kann doch jeder nachrechnen (mir ist das alles zuviel, um mit dem Formeleditor zu arbeiten, und mein Handgeschriebenes liest du ja doch nicht...). Also nochmals (nach Myon) "untere" und "obere" Bahnkurve (abermals ohne Einheiten - alles im SI-System):
y_1 = (-1/3)*x^2 + 1,267*x + 2
y_2 = (-0,276)*x^2 + 0,98*x + 2
Der Abwurfwinkel ergibt sich jeweil aus y´(0), der Betrag von v_0 habe ich aus Steigzeit t_s und v_0y(t_s)=0 bestimmt.
Selbstverständlich kann ich auf Wunsch auch die Rechnungen einstellen.
p.s. wo der Zappelphilipp herkommt ist mir rätselhaft
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 14. Apr 2020 09:57 Titel: Mathefix Verfasst am: 14. Apr 2020 09:57 Titel: |
 |
|
| blödi123 hat Folgendes geschrieben: | @Mathefix - betrachte doch nur mal - ganz ohne Physik - das Dreieck mit den Punkten (0/2), (1,5/2), (1,5/2, - Abwurfpunkt/untere Ringkante - Abwurfpunkt/untere Ringkante
da ist tan alpha = 0,8/1,5 und damit alpha=28° - beim schiefen Wurf ist der Abwurfwinkel bestimmt größer als 28°, jedenfalls kommt als untere Grenze keinesfalls 6,5° in Frage.
Den von Myon vorgeschlagenen Weg kann doch jeder nachrechnen (mir ist das alles zuviel, um mit dem Formeleditor zu arbeiten, und mein Handgeschriebenes liest du ja doch nicht...). Also nochmals (nach Myon) "untere" und "obere" Bahnkurve (abermals ohne Einheiten - alles im SI-System):
y_1 = (-1/3)*x^2 + 1,267*x + 2
y_2 = (-0,276)*x^2 + 0,98*x + 2
Der Abwurfwinkel ergibt sich jeweil aus y´(0), der Betrag von v_0 habe ich aus Steigzeit t_s und v_0y(t_s)=0 bestimmt.
Selbstverständlich kann ich auf Wunsch auch die Rechnungen einstellen.
p.s. wo der Zappelphilipp herkommt ist mir rätselhaft |
@blödi123
Vielen Dank für Deine Gleichungen. Da ist mir ins Auge gesprungen, dass ich anstatt mit h_0 = 2m mit h_0 =3 m gerechnet hatte.
Jetzt sind unsere Ergebnisse identisch.
Sorry für die Verwirrung.
|
|
 |
blödi123
Anmeldungsdatum: 17.01.2020
Beiträge: 56
|
 blödi123 Verfasst am: 14. Apr 2020 10:25 Titel: blödi123 Verfasst am: 14. Apr 2020 10:25 Titel: |
 |
|
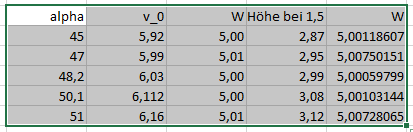
abschließend noch eine Bemerkung:
Die Fenster für Abwurfwinkel und Abwurfgeschwindigkeit sind ja "relativ eng" - ich habe mit Excel mal etwas experimentiert und gebe z.B. fünf Möglichkeiten für Abwurfwinkel und Geschw. an - notiert ist auch die Flughöhe, wenn der Ball den Ring erreicht
| Beschreibung: |
|
| Dateigröße: |
6.01 KB |
| Angeschaut: |
1763 mal |
|
|
|
 |
|
















 - Abwurfpunkt/untere Ringkante
- Abwurfpunkt/untere Ringkante
