| Autor |
Nachricht |
inkognito89
Anmeldungsdatum: 15.11.2019
Beiträge: 12
|
 inkognito89 Verfasst am: 09. Jan 2020 21:38 Titel: Bestimmungsgleichung für die Resonanzfrequenz inkognito89 Verfasst am: 09. Jan 2020 21:38 Titel: Bestimmungsgleichung für die Resonanzfrequenz |
 |
|
Hallo liebe Mitglieder!
Ich habe eine Frage bzgl. eines Problems bei dem ich mir erstens nicht sicher bin und zweitens Fragen habe  . .
Zu untersuchen ist ein gekoppelter elektrischer Schwingkreis mit folgendem DGL-System:

Nun habe ich es mit dQ/dt = I wie folgt umgewandelt

Ist das soweit korrekt?
Im nächsten Schritt möchte ich gerne die Bestimmungsgleichung für die Resonanzfrequenzen \omega der gekoppelten Kreise aufstellen. Dafür habe ich das Buch von Demtröder (Elektromagnetische Schwingungen und die Entstehung von elektromagnetischen Wellen; Experimentalphysik 2) herangezogen.
Leider weiß ich nicht wie ich weiter vorgehen kann bzw. ist mir dieses Vorgehen nicht bekannt. Außerdem würde ich gerne wissen, ob ich die Bestimmungsgleichung mit unterschiedlichen Induktivitäten recht einfach lösen kann?
Könnte mir bitte jemand helfen?
Viele Grüße
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 09. Jan 2020 23:51 Titel: Nils Hoppenstedt Verfasst am: 09. Jan 2020 23:51 Titel: |
 |
|
Hi,
das allgemeine Vorgehen besteht erstmal darin, aus dem System der gekoppelten Differentialgleichungen 2. Ordnung ein System 1. Ordnung zu machen. Führe dazu die beiden neuen Größen Q3 und Q4 ein, die wie folgt definiert sind:
Q3 := d/dt Q1
Q4 := d/dt Q2
wenn du dies in deine Ausgangsglechung einsetzt, erhältst du zusammen mit den beiden obigen Gleichungen ein System von 4 Diff'gleichungen 1. Ordnung. Nach Umsortieren und durch Einführung des Vektors Q^ := [Q1, Q2, Q3, Q4] bekommst du am Ende eine Matrixgleichung der Form:
A d/dt Q^ = B Q^
wobei in den 4x4 Matrizen A und B nur die Koeffizienten L1, L2, L12 und R stehen, also Konstanten sind.
Ich denke, ab hier kommst du alleine weiter.
Viel Erfolg!
Gruß,
Nils
|
|
 |
inkognito89
Anmeldungsdatum: 15.11.2019
Beiträge: 12
|
 inkognito89 Verfasst am: 10. Jan 2020 09:53 Titel: inkognito89 Verfasst am: 10. Jan 2020 09:53 Titel: |
 |
|
Hallo Nils,
vielen Dank für deine Antwort.
Ich habe das System 2.Ordnung mit Hilfe von einem impliziten Runge Kutta Verfahren gelöst (also numerisch).
Leider ist mir das mit der Bestimmungsgleichung wirklich nicht so klar.
Vielleicht kannst du mir bitte dafür gute und verständliche Literatur empfehlen?
Viele Grüße
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 10. Jan 2020 12:32 Titel: Nils Hoppenstedt Verfasst am: 10. Jan 2020 12:32 Titel: |
 |
|
Hi,
hier ist ein Link, wo ein paar Beispiele vorgestellt werden:
http://www.ieap.uni-kiel.de/et/people/wimmer/teaching/Phys_II/P2_V6.pdf
Zu deinem konkreten Problem: Mit dem Ansatz über die Matrixgleichung kommt eigentlich relativ einfach auf eine eindeutige Lösung. Wenn du noch Interesse hast, kann ich dir die Lösung posten. Könntest du mir bitte mal die Zahlenwerte für die Koeffizienten L1, L2, L12, C1 und R2 zukommen lassen? Ich würde gerne testen, ob die Lösung physikalisch sinnvoll ist (rein mathematisch ist sie das).
Viele Grüße,
Nils
|
|
 |
inkognito89
Anmeldungsdatum: 15.11.2019
Beiträge: 12
|
 inkognito89 Verfasst am: 13. Jan 2020 17:18 Titel: inkognito89 Verfasst am: 13. Jan 2020 17:18 Titel: |
 |
|
Hallo Nils,
entschuldige bitte vielmals meine späte Antwort. Ich habe mir den Link angeschaut und ganz konkrete Vorgaben habe ich leider für die Parameter nicht.
Es handelt sich hierbei um das Impulswiderstandsschweißen.
Hierfür ein paar Werte aus dem Internet und dem Buch von Demtröder
L_1 = 1, L_2 = 100, R_2 = 5*10^(-3), C_1 = 1F.

mit dem Kopplungsfaktor k in (0,1).
Damit sollte die Matrix nichtsingulär sein und demzufolge sollte das Problem eine eindeutige Lösung haben.
Falls du mir deine Lösung noch netterweise zeigen würdest, wäre ich dir sehr dankbar.
Viele Grüße
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 13. Jan 2020 21:46 Titel: Nils Hoppenstedt Verfasst am: 13. Jan 2020 21:46 Titel: |
 |
|
Hi,
ja klar, kein Problem. Bin froh, dass du dich noch gemeldet hast, hatte schon befürchtet alles umsonst gerechnet zu haben. ;-)
Also wie gesagt, besteht der Trick darin, die Diff'gleichungen in ein System 1. Ordnung umzuwandeln, indem man die zwei folgenden Größen einführt:

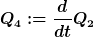
Wenn man dies in die Ausgangsgleichung einsetzt, erhält man nach Umsortierung folgendes Gleichungssystem:


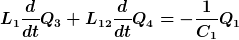

Dies kann man als Matrixgleichung schreiben:

Wir nennen die Matrix auf der linken Seite  , die Matrix auf der rechten Seite , die Matrix auf der rechten Seite 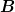 , setzen , setzen ) , multiplizieren die Gleichung von links mit , multiplizieren die Gleichung von links mit  und setzen und setzen  . Man erhält schließlich die sehr kompakte Form: . Man erhält schließlich die sehr kompakte Form:
 . .
Für die Lösung dieser Diff'gleichung machen wir den Ansatz:
 . .
Einsetzen des Ansatzes in die Matrixgleichung ergibt (nach Division mit 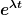 ) schließlich die Gleichung: ) schließlich die Gleichung:

Dies ist eine Eigenwertgleichung für die Matrix C. Da C eine 4x4 Matrix ist, gibt es i.A. vier Eigenwert/Eigenvektor-Paare. Jedes dieser Paare löst die Diff'gleichung. Die allgemeine Lösung ist dann eine Linearkombination dieser 4 Eigenlösungen.
Zuletzt bearbeitet von Nils Hoppenstedt am 13. Jan 2020 22:29, insgesamt 2-mal bearbeitet |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 13. Jan 2020 22:26 Titel: Nils Hoppenstedt Verfasst am: 13. Jan 2020 22:26 Titel: |
 |
|
Mal ein Zahlenbeispiel: Sei
 . .
Wenn man dies in die obigen Matrizen einsetzt und z.b. durch Hilfe mit Matlab die Eigenwerte der Matrix C berechnen lässt, erhält die folgenden 4 Eigenvektor/Eigenwert-Paare:




Diese 4 Paare ergeben eingesetzt in unseren Ansatz  vier unabhängige Lösungen, wobei uns nur die erste und zweite Zeile des Vektors interessieren, da diese den gesuchten Ladungen vier unabhängige Lösungen, wobei uns nur die erste und zweite Zeile des Vektors interessieren, da diese den gesuchten Ladungen 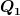 und und 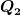 entsprechen. entsprechen.
Das erste Paar ergibt die triviale Lösung  , das zweite und dritte Paar ergeben zusammen eine gedämpfte Schwingung (man beachte, dass das Paar , das zweite und dritte Paar ergeben zusammen eine gedämpfte Schwingung (man beachte, dass das Paar ) die komplex Konjugierte des Paares die komplex Konjugierte des Paares ) ist, hier ergibt nur die Summe eine reellwertige Lösung) und das vierte Paar beschreibt eine exponentiellen Abfall. Die allgemeine Lösung ist dann eine Linearkombination dieser drei Basislösungen. ist, hier ergibt nur die Summe eine reellwertige Lösung) und das vierte Paar beschreibt eine exponentiellen Abfall. Die allgemeine Lösung ist dann eine Linearkombination dieser drei Basislösungen.
Viele Grüße,
Nils
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 13. Jan 2020 22:42 Titel: Nils Hoppenstedt Verfasst am: 13. Jan 2020 22:42 Titel: |
 |
|
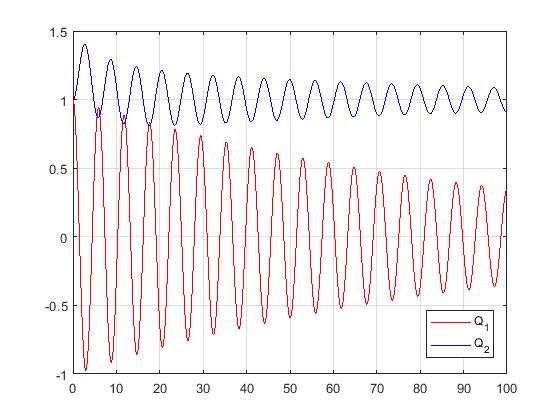
Und so sieht die Lösung für Q1(t) und Q2(t) aus, wenn man die Basislösungen einfach alle addiert (siehe Anhang).
Gruß,
Nils
| Beschreibung: |
|
| Dateigröße: |
38.47 KB |
| Angeschaut: |
1387 mal |
|
|
|
 |
inkognito89
Anmeldungsdatum: 15.11.2019
Beiträge: 12
|
 inkognito89 Verfasst am: 14. Jan 2020 11:58 Titel: inkognito89 Verfasst am: 14. Jan 2020 11:58 Titel: |
 |
|
Hallo Nils,
vielen Dank für deine ausführliche Antwort und deine große Mühe.
Ich werde meine numerische Lösung definitiv mit deiner exakten Lösung vergleichen (danke Python  ). ).
Ich denke jetzt ist mir das mit der Bestimmungsgleichung auch klar, denn wir leiten hier I_1 und I_2 (gegeben durch den Ansatz) nach t ab, setzen ein und können dann die resultierenden Gleichungen gleichsetzen um die Resonanzfrequenzen zu ermitteln.
Ich denke ab dem Schritt sollte der aperiodische Grenzfall nicht mehr so schwer sein und ich kann auch die Untersuchung für R->0 starten.
Vielen Dank und weiterhin noch viel Vergnügen im Forum.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 14. Jan 2020 12:58 Titel: Nils Hoppenstedt Verfasst am: 14. Jan 2020 12:58 Titel: |
 |
|
Gerne, war ne interessante Aufgabe!
Noch ein Wort zur Resonanzfrequenz: Die Resonanzfrequenz (oder besser gesagt Eigenfrequenz) ist einfach der Imaginärteil derjenigen der 4 Eigenvektoren, die komplex sind. Im obigen Beispiel also  und und  . .
Um das zu sehen, schreiben wir einfach mal die ersten Komponente von  als als =re^{i \phi}) und den komplexen Eigenwert als und den komplexen Eigenwert als 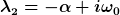 . Der zeitliche Verlauf von . Der zeitliche Verlauf von ) , der sich aus der Summe der 2. und 3. Eigenlösung ergibt, ist also: , der sich aus der Summe der 2. und 3. Eigenlösung ergibt, ist also:
 &=& \vec{W}_2(1)e^{\lambda_2 t} + \vec{W}_3(1)e^{\lambda_3 t}\\&=& re^{i \phi}e^{-\alpha t + i\omega_0 t}+ r e^{-i\phi}e^{-\alpha t - i\omega_0 t}\\&=&2re^{-\alpha t}\cos(\omega_0 t + \phi))
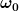 spielt hier also tatsächlich die Rolle der Eigenfrequenz. spielt hier also tatsächlich die Rolle der Eigenfrequenz.
Viele Grüße,
Nils
|
|
 |
|
















 .
.
