| Autor |
Nachricht |
lucabla
Gast
|
 lucabla Verfasst am: 20. Okt 2019 00:14 Titel: SRT: Beschleunigte Bewegungen und Vierervektoren lucabla Verfasst am: 20. Okt 2019 00:14 Titel: SRT: Beschleunigte Bewegungen und Vierervektoren |
 |
|
Hey, ich bin Mathematikstudent mit Anwendungsfach Physik und null Fähigkeiten darin.
Nun ist die erste Hausübung in Analytischer Mechanik und Spezieller Relativitätstheorie so langsam fällig und ich habe einen Haufen Fragen dazu, da in der Vorlesung gefühlt nichts zu all dem erklärt wurde. Hier der Aufgabentext:
"Beim Flug einer Rakete ist eine gleichmäßig beschleunigte Bewegung dadurch definiert, dass der Astronaut zu allen Zeiten mit der gleichen Kraft in den Sitz gedrückt wird. Finden Sie die Weltlinie einer solchen Bewegung in Eigenzeit-Parametrisierung. Betrachten Sie dazu die Weltlinie, die sich ergibt wenn man einen raumartigen Punkt, z.B. (0,a,0,0) der einparametrigen Untergruppe der Schübe unterwirft, also =\begin{pmatrix} a\sinh(\lambda)\\ a\cosh(\lambda)\\0\\0\end{pmatrix}) " "
Erste Aufgabe war nun, zu zeigen, dass diese Weltlinie eine Hyperbel beschreibt, das habe ich hinbekommen.
Nun soll man zeigen, dass der Betrag der Vierergeschwindigkeit  konstant ist. Dann steht dort noch "Dadurch können wir die Eigenzeit proportional zu konstant ist. Dann steht dort noch "Dadurch können wir die Eigenzeit proportional zu  ansetzen. Parametrisieren Sie die Vierergeschwindigkeit mit der Eigenzeit ansetzen. Parametrisieren Sie die Vierergeschwindigkeit mit der Eigenzeit 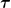 , so dass gilt , so dass gilt  ." Damit habe ich gleich mehrere Probleme: ." Damit habe ich gleich mehrere Probleme:
1. Was genau ist die Vierergeschwindigkeit? Das Internet (ich habe leider bis jetzt noch kein gutes Buch gefunden, dass dieses Thema so erklärt) sagt, dass in der ersten Komponente der Vierergeschwindigkeit nach Ableitungsregeln stets nur Lorentzfaktor multipliziert mit der Lichtgeschwindigkeit steht (siehe etwa Wikipedia "Vierervektor"), nun steht hier aber eine Hyperbelfunktion in der ersten Komponente, das verstehe ich nicht.
2. Was ist überhaupt lambda? Soll es die Zeit (etwa aus einem Inertialsystem gemessen) sein? Das wäre ja wichtig, um zu wissen, wie man nun nach der Eigenzeit parametrisiert. Apropos:
3. Was heißt "parametrisieren nach der Eigenzeit"?
4. Außerdem: Welcher Betrag ist überhaupt gemeint? Ist es die vom Standardskalarprodukt induzierte Norm oder die vom Lorentzskalarprodukt? In einer späteren Aufgabe wird explizit noch vom Lorentzbetrag (statt Betrag) gesprochen, also tendiere ich eher zu ersterem. Diese Frage würde sich wahrscheinlich klären wenn ich wüsste was die Vierergeschwindigkeit genau ist und wie ich sie berechne.
Sollte ich das verstehen werden sicher auch die anderen Aufgabenteile funktionieren.
Verzweifelte Grüße |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 20. Okt 2019 09:19 Titel: TomS Verfasst am: 20. Okt 2019 09:19 Titel: |
 |
|
Die Eigenzeit tau ist die auf einer mit einem Beobachter mitbewegte Uhr; sie musst demnach dessen Zeit in seinem Ruhesystem.
Die Vierergeschwindigkeit u ist die Ableitung des Ortsvektors x in der 4-dim. Raumzeit nach der Eigenzeit

Im Ruhesystem eines (massebehafteten) Beobachters gilt für dessen Vierergeschwindigkeit
)

Da u ein Vierervektor und sein Quadrat daher ein Lorentz-Skalar ist, gilt die zweite Beziehung für die Bahnkurve offenbar in jedem System.
lambda ist ein beliebiger Parameter, der die Bahnkurve parametrisiert. Die Parametrisierung mittels Eigenzeit besagt letztlich, dass
 = x^\mu(\lambda(\tau)))
gewählt werden kann.
Mit dem Quadrat oder „Betragsquadrat“ eines Vierervektors a ist immer das vom o.g. Skalarprodukt des Vierervektors induzierte gemeint. Da das Skalarprodukt nicht positiv definit ist, liegt keine Norm vor.
Man spricht von zeitartigen, raumartigen, lichtartigen Vierervektoren a, wenn

gilt *).
Beispiele sind Vierergeschwindigkeit von massebehafteten Objekten, Vierergeschwindigkeit von masselosen Objekten, Verbindungslinien zweier aus Sicht eines Beobachters gleichzeitigen Ereignisse wie z.B. der Vektor entlang eines Meterstabes.
*) Achtung: in der Literatur findet sich auch die umgekehrte Konvention
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















