| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 05. Apr 2019 15:58 Titel: Warum ist der Trägheitstensor kovariant zweiter Stufe Corbi Verfasst am: 05. Apr 2019 15:58 Titel: Warum ist der Trägheitstensor kovariant zweiter Stufe |
 |
|
Meine Frage:
Auf Wikipedia steht, dass der Trägheitstensor ein kovarianter Tensor zweiter Stufe ist.
Im Nolting ist er definiert als:
)
wie kann man jetzt zeigen, oder woran erkennt man, dass dieser Tensor zweifach kovariant ist?
Und wenn sich der Drehimpuls aus der Anwendung des Trägheitstensors auf die Winkelgeschwindigkeit ergibt (die ja einen kontravarianten Vektor darstellt) würde man ja einen kovarianten Vektor für den Drehimpuls erhalten oder?
Meine Ideen:
Ich versteheh schon nicht warum das Kronecker-Symbol hier zweifach kovariant ist, das habe ich auch schon so gesehen:  . .
Ich verstehe ebenfalls nicht warum die Komponenten x_il und x_im den Index unten haben. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Apr 2019 16:54 Titel: Re: Warum ist der Trägheitstensor kovariant zweiter Stufe index_razor Verfasst am: 05. Apr 2019 16:54 Titel: Re: Warum ist der Trägheitstensor kovariant zweiter Stufe |
 |
|
| Corbi hat Folgendes geschrieben: | Meine Frage:
Auf Wikipedia steht, dass der Trägheitstensor ein kovarianter Tensor zweiter Stufe ist.
Im Nolting ist er definiert als:
)
wie kann man jetzt zeigen, oder woran erkennt man, dass dieser Tensor zweifach kovariant ist?
Und wenn sich der Drehimpuls aus der Anwendung des Trägheitstensors auf die Winkelgeschwindigkeit ergibt (die ja einen kontravarianten Vektor darstellt) würde man ja einen kovarianten Vektor für den Drehimpuls erhalten oder?
|
Ja, da hast du recht. Die Behauptungen im wikipedia-Artikel sind strenggenommen nicht konsistent. Legt man, wie in dem Artikel, die Beziehung

zugrunde, spricht das für einen 1fach ko- und 1fach kontravarianten Tensor 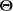 . .
Das macht aber nichts weiter, denn da der Raum euklidisch ist, kann man kovariante und kontravariante Indizes ineinander umwandeln:

etc, wobei 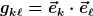 der metrische Tensor des Raumes ist. der metrische Tensor des Raumes ist.
Eine mangelnde Unterscheidung zwischen kovarianten und kontravarianten Indizes wird dir in euklidischen Räumen immer wieder begegnen. Die Rechtfertigung dafür ist die Identifizierung von Tangential- und Kotangentialraum vermöge der "musikalischen Isomorphismen". |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 06. Apr 2019 19:56 Titel: Corbi Verfasst am: 06. Apr 2019 19:56 Titel: |
 |
|
Dann haben Aussagen über das Transformationsverhalten von Tensoren die im euklidischen Raum definiert sind ja eigentlich garkeinen Sinn oder? Weil ich den Trägheitstensor dann ja genau so gut also kontravarianten oder gemischten Tensor definieren kann.
Was mich auch verwirrt ist, dass im Nolting steht, dass Tensoren immer ein bestimmtes Transformationsverhalten aufweisen während Matrizen ein beliebiges Transformationsverhalten aufweisen. Aber müssen sich Matrizen nicht immer wie gemischte Tensoren(2.Stufe) transformieren? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Apr 2019 12:12 Titel: index_razor Verfasst am: 07. Apr 2019 12:12 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | Dann haben Aussagen über das Transformationsverhalten von Tensoren die im euklidischen Raum definiert sind ja eigentlich garkeinen Sinn oder? Weil ich den Trägheitstensor dann ja genau so gut also kontravarianten oder gemischten Tensor definieren kann.
|
Das sind dann immer noch zwei verschiedene Tensoren, auch wenn sie wahrscheinlich beide als "Trägheitstensor" bezeichnet werden. Sie besitzen auch unterschiedliches Transformationsverhalten. Es ist im euklidischen Raum aber egal mit welchem Transformationsgesetz du einen speziellen Tensor 2. Stufe definierst.
| Zitat: |
Was mich auch verwirrt ist, dass im Nolting steht, dass Tensoren immer ein bestimmtes Transformationsverhalten aufweisen während Matrizen ein beliebiges Transformationsverhalten aufweisen. Aber müssen sich Matrizen nicht immer wie gemischte Tensoren(2.Stufe) transformieren? |
Eine Matrix ist nur ein Zahlenschema. Ohne präzise Definition der Bedeutung dieser Zahlen ist jede Aussage über ihr Transformationsverhalten sinnlos.
Man kann aber z.B. jeder Matrix  zusammen mit einer Basis zusammen mit einer Basis 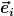 des Vektorraums des Vektorraums 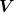 einen Endomorphismus einen Endomorphismus  zuordnen, nämlich zuordnen, nämlich
=\sum_{ik}v^i A_{ki}\vec{e}_k)
Das ist noch kein Tensor, wie man ihn normalerweise definiert. Aber tatsächlich gehört zu jedem Endomorphismus wiederum ein gemischter Tensor  2. Stufe, im Sinne einer multiliniearen Abbildung eines Vektors und eines Kovektors auf die reellen Zahlen 2. Stufe, im Sinne einer multiliniearen Abbildung eines Vektors und eines Kovektors auf die reellen Zahlen
\stackrel{\text{def}}{=}\langle \omega, T(v)\rangle) . .
Der Tensor 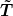 hat bzgl. hat bzgl. 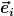 und der dualen Basis und der dualen Basis 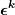 genau genau  als Komponentenmatrix, denn als Komponentenmatrix, denn
\rangle = \sum_\ell A_{\ell i}\langle \epsilon^k, \vec{e}_\ell\rangle = \sum_\ell A_{\ell i}\delta^k_\ell=A_{k i})
In diesem Sinne erbt jetzt also die Matrix  das Transformationsverhalten von das Transformationsverhalten von 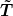 . Aber nur deshalb weil ich definiert habe, daß . Aber nur deshalb weil ich definiert habe, daß  die Komponenten eines Tensors die Komponenten eines Tensors 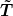 bzgl. einer konkreten Basis bzgl. einer konkreten Basis 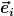 und der dazugehörigen Dualbasis sein sollen. und der dazugehörigen Dualbasis sein sollen. |
|
 |
|
|















